基于加权非负最小二乘的颗粒粒径反演方法研究

2023-11-08岳朴杰张世玮俞天阳

测试技术学报 2023年6期

岳朴杰, 张世玮, 孟磊, 宁翔, 俞天阳

(1. 大唐环境产业集团股份有限公司, 北京 100097; 2. 上海理工大学上海市动力工程多相流动与传热重点实验室, 上海 200093)

0 引言

近年来, 两相流中颗粒粒径测量问题受到国内外广泛关注和研究, 如能源、化工、制药和环保等行业中各种悬浊液和乳剂的颗粒在线测量问题[1-3]。其中颗粒的形状、粒径分布及存在状态对工业产品的性能质量、生产效率和安全均有重要影响, 因此, 对两相介质中颗粒物特征参数的测量显得尤为重要[4-5]。在众多颗粒尺寸测量技术中, 超声波具有较强的穿透性、测量范围宽、适合高浓度体系的非接触式测量等特点, 同时有测量装置简单、易实现在线检测等优势[6-8]。超声波在两相体系中传播与颗粒发生相互作用并产生衰减, 得到的超声衰减谱包含被测颗粒系的粒径信息, 结合ECAH(Epstein-Carhart-Allegra-Hawley), McC(McClements), BLBL(Bouguer-Lambert-Beer-Law)等模型预测, 构造目标函数进一步经反演计算可得到颗粒系的粒径分布[9-11]。

实验衰减谱的测量、理论模型的建立和反演计算是超声衰减谱法颗粒测量的3个主要过程, 其中, 反演算法直接关系到颗粒粒径分布求解的精度。反演方法可以分为非独立模式算法和独立模式算法。非独立模式算法通常需事先假定颗粒系的粒径分布遵循某种函数形式, 然后以理论预测和实际测量的衰减谱误差作为目标函数来构造最优化问题[12-14]。但大多数情况下并不知道颗粒系粒径分布情况, 通常采用无函数约束的独立模式求解方法, 利用正则化技术克服方程的病态问题, 引入正则化因子和光顺矩阵, 采用非负最小二乘算法进行超声谱的反演得到颗粒系粒径分布[15-16]。

在使用超声系统测量悬浊液或乳剂的实验衰减谱过程中, 不可避免地会带来测量误差, 但非负最小二乘算法并未考虑该误差对求解粒径分布的影响。文章提出一种基于最优正则化的加权非负最小二乘OrtWtls(Optimum regularization technique Weighted total least squares)算法, 反演颗粒系的粒径分布, 以不同粒径和信噪比的理论衰减谱对该算法进行验证。此外, 将此算法应用于不同浓度石灰石浆液粒度分布的反演计算, 并采用图像法对其结果进行验证。

1 加权最小二乘粒径反演

1.1 独立模式算法求解粒径分布

颗粒粒径分布测量原理是基于不同粒径产生的超声谱特性差异, 通过寻找理论和试验数据之间的最佳拟合值确定。借助波的散射理论联系单个颗粒的散射效应和整个离散颗粒群的宏观效果, 得到悬浊液中的复波数[17], 进一步求解得到的超声衰减系数

(1)

式中:αs表示超声衰减系数;An为散射系数;φ为体积浓度;kc为连续介质波数;R为颗粒半径;ω为角频率;qi为颗粒半径在第i个尺寸区间[Ri,Ri+1]的体积分数;n为颗粒粒径分散等级; Re为取实部运算。

为获得准确的粒径分布, 将模型改写为标准数学求解问题, 改变系数矩阵和超声谱向量, 将式(1)离散并在多频条件下转化为线性方程形式[18]

AF=G,

(2)

式中:A是系数矩阵;F是待求的离散化颗粒尺寸体积分布;G是由不同频率下的实验超声谱组成的向量。

该矩阵方程非适定且高度病态, 常用矩阵求逆无法得到准确结果, 通常由最优正则化(ORT, Optimum Regularization Technique)算法结合非负最小二乘求解[19-20], 通过引入正则化因子γ和光顺矩阵H, 对病态方程进行改善, 提高解的稳定性。表达式为

F=(ATA+γH)-1ATG,

(3)

式中:AT表示A的转置矩阵;γ称正则化因子, 表示矩阵的权重。

1.2 加权最小二乘求解粒径分布

为减小两相介质中超声衰减谱的测量误差对粒径分布求解精度的影响, 提出一种最优正则化算法结合加权最小二乘, 求解颗粒系粒径分布。引入权重矩阵W, 粒径分布求解公式表达式为

F=(ATWA+γH)-1ATWG。

(4)

在OrtWtls算法中, 正则化参数的选择较为关键, 该参数的确定取决于系数矩阵A, 测量向量G的误差程度以及颗粒粒径分布的光滑程度。鉴于在颗粒测量问题中很难估计测量向量G的误差水平, 因此常使用广义交叉检验(Generalized Cross Validation, GCV)准则和L曲线准则(L-Curve)对正则化因子进行优化[21]。其中GCV准则考虑测量向量中各元素都应被相应的正则解预测, 且正则化参数与G的正交变换无关。经推导,γ可归结为对式(5)求最小值来确定[22]。

(5)

式中:I为单位矩阵;m为所用频率数目, 也是单位矩阵的阶数, 上标T为矩阵转置运算, 符号Trace是求矩阵的迹。

式(6)为超声衰减谱权重矩阵W的计算公式

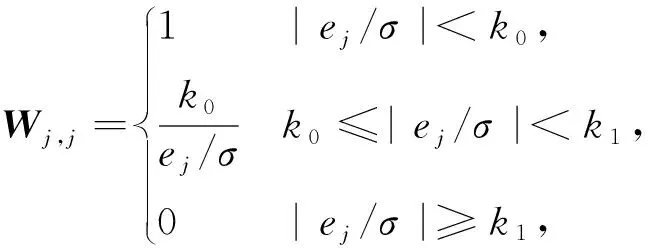
(6)

式中:ej为超声衰减谱与其拟合谱的残差绝对值;σ为ej的标准差。根据式(6)将超声衰减谱的残差分为3类:① 残差不是粗大误差, 残差ej小于k0σ, 权重因子为1;② 残差可能是粗大误差, 此时残差ej在k0σ和k1σ之间, 权重因子为k0/(|ej/σ|);③ 残差是粗大误差, 此时残差ej大于k1σ, 权重因子为0。通常取k0为1.5,k1为2.5[23-24]。

图1 为OrtWtls算法流程图, 基于ORT算法结合加权最小二乘反演颗粒系粒径分布。

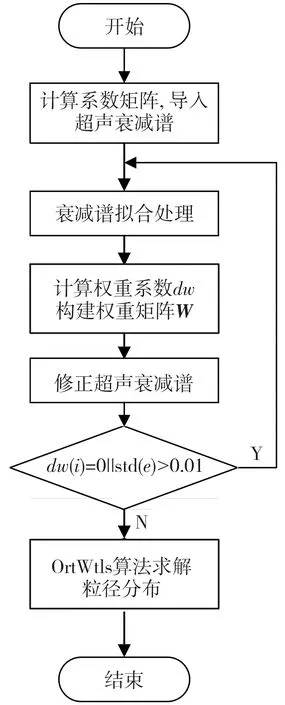
图1 OrtWtls算法流程图Fig.1 Flow chart of OrtWtls algorithm

由权重系数dw构建权重矩阵W, 并根据权重系数对实验超声衰减谱进行修正, 直至权重系数dw中无粗大误差或残差的标准差小于0.01结束迭代。与最小二乘算法相比, 加权最小二乘使超声衰减谱中具有粗大误差的权重系数置零, 能够有效降低实验衰减谱测量误差对反演结果的影响。

2 数值模拟

2.1 OrtWtls算法验证

为验证OrtWtls算法的性能, 以体积浓度1%的水-玻璃微珠悬浊液为研究对象, 采用McC+BLBL理论模型分别计算颗粒直径10 μm～80 μm悬浊液中的理论超声衰减谱。使用GCV准则对γ参数进行优化,V(γ)函数取最小值时对应的γ即为最优正则化因子, 不同粒径下的计算结果如表1 所示。经分析计算可知, 对上述直径10 μm～80 μm的理论衰减谱进行三阶多项式拟合处理, 其相关系数均值为0.999 8, 因此, 不同粒径下的超声衰减谱可用三阶多项式近似表达。

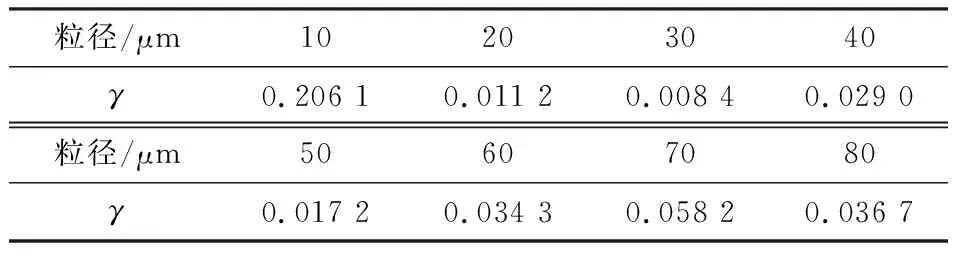
表1 不同粒径的正则化因子Tab.1 Regularization factors of different particle sizes

基于上述分析, 使用OrtWtls反演颗粒系的粒径分布, 计算不同算例粒径分布的体积中位径DV50(小于该直径的颗粒体积各占颗粒总体积的50%), 并与设定直径进行对比, 如图2 所示。反演结果相对误差均小于5%, 验证了OrtWtls算法的计算准确性。

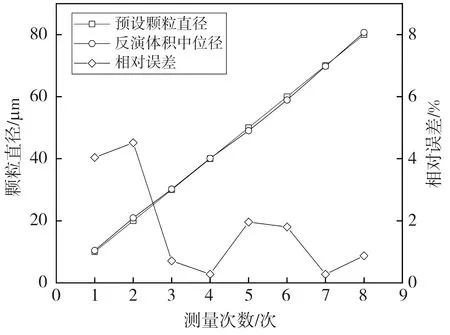
图2 设定直径与OrtWtls反演结果对比Fig.2 Comparison between set diameter and inversion result of OrtWtls

2.2 抗噪性分析

在实验超声衰减谱获取过程中, 不可避免会引入测量误差, 为模拟实验过程中带来的随机干扰和测量误差, 在理论衰减谱中加入随机噪声, 使其信噪比分别为10 dB, 20 dB, 使用OrtWtls算法反演颗粒系的粒径分布。为分析提出算法的鲁棒性, 统计连续20组含噪衰减谱的反演结果, 并与预设直径和Twomey算法[25]计算结果进行对比。图3 为信噪比10 dB时不同粒径的理论和含噪衰减谱, 图4 为含噪衰减谱分别由Twomey和OrtWtls算法计算得到的颗粒系粒径分布。

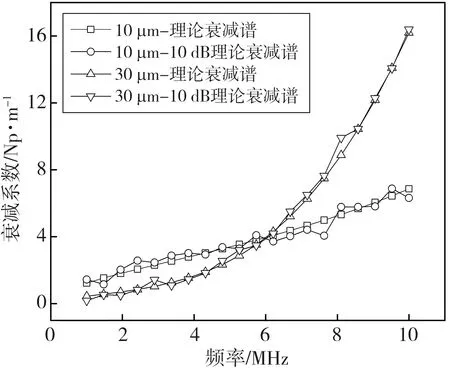
图3 信噪比10 dB超声衰减谱Fig.3 Ultrasonic attenuation spectrum of signal noise ratio 10 dB

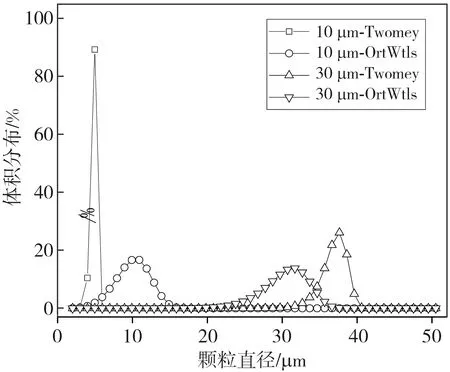
图4 不同算法反演结果对比Fig.4 Comparison of calculation results of different algorithms

由图3 中超声衰减谱可知, 含噪衰减系数随超声频率的变化趋势与理论衰减谱基本一致, 但个别频率下衰减系数的残差为粗大误差, 致使图4 中Twomey算法得到的DV50与预设直径差异较大, 颗粒直径10 μm, 20 μm, 30 μm, 40 μm时的相对误差分别为55.3%, 16.4%, 23.8%, 14.6%。而对超声衰减谱做加权处理的OrtWtls算法得到的特征参数DV50与设定直径基本一致, 不同粒径下的相对误差均小于5%。表2 为信噪比10 dB超声衰减谱连续20次计算粒径分布DV50的统计结果。

表2 10 dB衰减谱粒径分布统计结果Tab.2 Statistical results of particle size distribution of 10 dB attenuation spectrum

图5(a) 为信噪比10 dB衰减谱的粒径分布统计结果。相比Twomey算法, 提出的OrtWtls算法得到的特征参数DV50与设定直径更接近, 不同粒径下相对误差分别为4.0%, 2.1%, 1.4%, 1.2%。为分析OrtWtls算法在不同信噪比下的抗噪性, 表3 给出了信噪比20 dB衰减谱连续20次计算粒径分布DV50的均值、方差和标准差, 图5(b) 为该信噪比下的粒径分布统计结果。

表3 20 dB衰减谱粒径分布统计结果Tab.3 Statistical results of particle size distribution of 20 dB attenuation spectrum

(a) 信噪比10 dB衰减谱结果统计

由图5 可知, 对于信噪比10 dB和20 dB的衰减谱, 不同粒径时OrtWtls算法得到的DV50与设定直径误差均小于5%, 且多次计算的标准差均小于1 μm。设定颗粒直径10 μm时, OrtWtls算法得到的特征参数DV50与设定值基本一致, 且标准差为0.43 μm, 而Twomey算法的计算结果偏差较大。当颗粒直径大于20 μm时, 两种算法得到的DV50与设定值基本一致, 但OrtWtls算法标准差明显小于Twomey算法。提出的OrtWtls算法对于含噪超声衰减谱的反演具有较好的鲁棒性, 能够准确计算颗粒系的粒径分布。

3 实测颗粒反演计算

3.1 实验原理和装置

图6 为基于超声法原理测量浆液粒度的实验系统。样品池宽度12.5 mm, 在厚度10 mm的有机玻璃缓冲块两端分别安装超声发射、接收换能器(Olympus V310, 探头频率5 MHz), 使用CTS-8077PR信号发射接收器激励超声换能器产生超声波, 另一换能器接收经被测浆液后的超声透射信号, 经信号放大后选用NI-PCI-5114高速A/D卡(采样率250 MHz)完成对超声信号的采集。对超声信号进行频谱分析, 得到被测浆液的衰减谱, 最终经数值反演得到被测浆液的粒径分布。

图6 超声测量系统示意图Fig.6 Schematic diagram of ultrasonic measurement system

以石灰石粉末分别配置质量浓度为10%, 20%的浆液, 使用BT-1600光学显微镜观察浆液颗粒的大小和形态, 图7 为经稀释后的石灰石浆液光学显微镜图片。使用ImageJ图像分析软件对相同试样的10张显微镜图片进行分析, 统计得到石灰石浆液的粒径分布。

图7 石灰石浆液显微镜图片Fig.7 Microscope image of limestone slurry

3.2 实验数据与分析

超声衰减系数可以通过超声波穿过浆液和背景介质的信号幅值差异来计算, 采用透射法测量浆液衰减系数的表达式为[26]

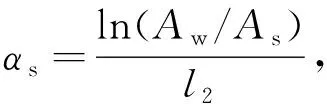
(7)

式中:Aw为背景介质的透射信号幅值;As为被测浆液的透射信号幅值,l2为测量区的宽度。多个超声频率的衰减系数即可组成实验超声衰减谱。

使用图6 测量系统, 分别采集质量浓度10%, 20%浆液超声透射信号并计算超声衰减谱, 结果如图8 所示。超声衰减系数均随超声频率的增加而增大, 近似呈线性变化趋势。另外, 由于浆液中单位体积内的颗粒数目随浆液浓度的增加而增大, 对超声波能量的耗散增强, 故质量浓度20%的衰减系数较10%时的大。根据不同浓度浆液的实验超声衰减谱, 分别使用OrtWtls和Twomey算法求解浆液的粒径分布, 并与图像法的统计结果做对比, 结果如图9 所示。

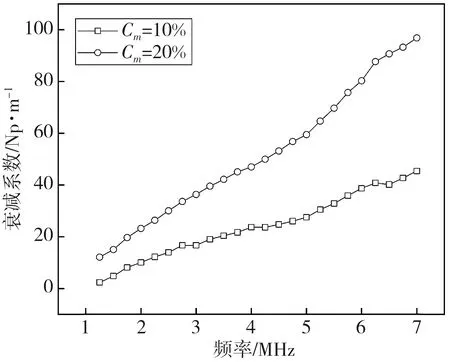
图8 石灰石浆液超声衰减谱Fig.8 Ultrasonic attenuation spectrum of limestone grout

图9 超声法与图像法粒径分布对比Fig.9 Comparison of particle size distribution between ultrasonic and image method

由图9 中的粒径分布可知, 浆液质量浓度为10%和20%时, OrtWtls算法得到的粒径分布DV50分别为9.50 μm, 9.67 μm, 与图像法体积中位径8.82 μm的测量结果基本吻合, 且不同浓度下的相对误差分别为7.71%和9.64%。但Twomey算法并未得到确切的粒径分布, 这是因为该算法没有对超声衰减谱的测量误差进行处理。对于实验得到的含噪超声衰减谱, 文章提出的OrtWtls算法通过加权处理能有效减小反演误差, 准确计算石灰石浆液的粒径分布。