核电厂安全壳结构钢衬里力学行为研究进展
2023-11-08王冬梅
金 松,王冬梅,蒋 迪
(1.安徽工业大学建筑工程学院,安徽 马鞍山 243000,2.中国核电工程有限公司,北京 100840)
核能作为新兴清洁能源发展中的领跑者,以其高能量、少耗料、高效率且废弃物产生量小而受到广泛青睐。截至2021 年年底,我国大陆地区共有在建和运行核电机组71 台,其中运行机组52 台[1]。由于核电厂系统本身的复杂性和人类认知的局限性,历史上曾发生过一些惨痛的核事故,这些核事故造成重大人员伤亡和经济损失,给核电抹上了灰色的阴影。核电厂采用纵深防御的设计理念来保证核电厂安全。安全壳结构作为最后一道防线,其功能是防止事故的放射性产物释放到外部环境中[2-4]。钢衬里作为重要的防泄漏屏障,对保证安全壳结构完整性至关重要。然而事故工况下的荷载影响钢衬里防泄漏功能,同时由于钢衬里锚固系统复杂的几何特性、钢衬里与混凝土相互作用使得钢衬里的力学行为和相关性能变得十分复杂。目前关于钢衬里的力学行为和力学性能研究以国外研究为主,国内处于起步阶段。此外深入了解钢衬里力学行为和相关力学性能对提升钢衬里的密封性能乃至于保证核电厂安全运行至关重要。
基于上述背景,本文对国外安全壳结构钢衬里力学行为研究进行总结归纳,详细阐述安全壳结构钢衬里撕裂失效机理,钢衬里锚固系统以及钢衬里屈曲行为研究现状及相关进展并指出当前研究存在的问题以及后续需要深入研究的问题。
1 钢衬里力学行为试验研究
内层安全壳为带钢衬里的预应力混凝土安全壳,主要用来抵抗内部灾害。内层预应力混凝土安全壳的结构高度约70 m,内径约为45 m,壁厚在1.0~1.5 m;其结构简图如图1 所示。钢衬里一般采用延性较好的5~10 mm 厚的低碳钢制作而成[5]。在设计中一般不考虑其强度,钢衬里在安全壳结构里一般采用栓钉和角钢与混凝土进行连接[6][见图1(b)]。钢衬里的作用是确保密封性并且当作浇筑混凝土的内模板[7-12]。
1.1 钢衬里撕裂机理研究
安全壳结构钢衬里在事故工况内压荷载作用下钢衬里撕裂现象产生主要由于局部钢衬里应变集中,这种应变集中主要是由于混凝土开裂后,钢衬里与混凝土产生相对滑移,钢衬里滑移受到锚固体系约束使得钢衬里产生应变集中进而导致钢衬里发生撕裂。钢衬里在事故内压荷载作用下的撕裂如图2 所示。
1988 年和2003 年美国桑迪亚国家实验室分别进行了1:6 钢筋混凝土安全壳模型试验[13]和1:4 预应力混凝土模型试验[14]。1:6 钢筋混凝土安全壳模型试验的钢衬里撕裂位置出现在贯穿件附近的钢衬里加厚区位置(见图3)。1:4预应力混凝土安全壳模型试验在设备闸门附近钢衬里发生撕裂(见图4),同时在钢衬里发生撕裂后试验无法继续加压。两个模型试验得出的一致结论是:钢衬里撕裂失效是安全壳结构的主要失效模式,造成钢衬里撕裂现象产生的主要原因是钢衬里应变集中。

图3 1:6 钢筋混凝土安全壳试验钢衬里撕裂Fig.3 Tearing of the steel liner in the 1:6 scale reinforced concrete containment test

图4 1:4 预应力混凝土安全壳结构模型试验钢衬里撕裂Fig.4 Tearing of steel liner in the 1:4 pre-stressed concrete containment structure test
在桑迪亚国家实验室进行的安全壳模型试验之后,研究人员充分认识到钢衬里撕裂是安全壳泄漏失效的控制因素,后续开展了安全壳局部部位缩尺模型试验。
安全壳局部缩尺模型试验研究表明[15-17]:钢衬里的细部连接构造、锚固体系以及钢衬里与混凝土相互作用对钢衬里的撕裂行为影响很大,钢衬里很高的局部应变可以造成钢衬里发生撕裂进而导致安全壳结构发生泄漏。
此外,安全壳结构局部足尺模型试验研究表明[18,19]:安全壳结构失效是刚度不连续区域钢衬里与混凝土复杂相互作用造成的钢衬里应变集中进而导致钢衬里撕裂产生(见图5),同时这些试验进一步证明了泄漏失效比安全壳结构整体失效更有可能发生。

图5 安全壳局部足尺模型试验结果Fig.5 Results of local containment full-scale model
综合上述研究成果可以发现:安全壳结构钢衬里撕裂是安全壳泄漏的控制指标,同时钢衬里撕裂主要发生在诸如贯穿件等不连续区域,钢衬里撕裂的主要原因是钢衬里局部变形集中造成的。
1.2 钢衬里其他性能试验研究
针对钢衬里其他诸如稳定性及其锚固体系性能,国外学者也进行了一些试验研究,钢衬里相关锚固系统试验研究表明钢衬里撕裂失效不会早于锚固系统失效,钢衬里屈曲不会发生在钢衬里屈服之前,增加钢衬里屈服强度会增加钢衬里锚固体系的受力和变形,增加钢衬里厚度会减小其受力和变形,传统数值计算方法得到的荷载-挠度曲线偏于保守[20-23]。
2 钢衬里力学行为数值模拟研究
2.1 钢衬里撕裂行为数值模拟
关于钢衬里撕裂问题,国外一些学者试图通过数值模拟方法来分析和解释安全壳结构钢衬里撕裂机理。钢衬里相关数值模拟分析表明[24-28]:钢衬里撕裂主要原因是钢衬里与其锚固体系相对滑移产生的剪力引起钢衬里应变集中,同时钢衬里撕裂受到锚固体系及细部构造影响,这些数值模拟研究也间接印证了桑迪亚实验室1:6 钢筋混凝土安全壳模型试验及1:4 预应力混凝土安全壳模型试验中钢衬里撕裂发生的机理。
2.2 钢衬里其他相关力学行为数值模拟研究
钢衬里及锚固体系相关数值模拟研究表明:在正常运行和失水事故情况下钢衬里没有屈曲及其锚固体系发生失效的风险,需要关注钢衬里锚固区域混凝土压碎造成的失效[29,30]。钢衬里施工过程的稳定性精细化有限元分析表明:初始缺陷对钢衬里极限承载力影响较小[31,32]。
综合钢衬里其他相关行为数值模拟研究发现,需要建立精细化安全壳结构钢衬里及其锚固系统分析模型并且综合考虑多种因素的影响对预测钢衬里及其锚固体系的力学行为十分重要。
3 钢衬里力学行为理论分析与研究
在试验和数值模拟分析的基础上,国外一些学者通过理论分析建立安全壳结构钢衬里力学行为的理论分析模型。相关理论分析模型为后续钢衬里研究提供了重要技术支撑。钢衬里的力学行为理论研究主要可以归纳为以下两大方面。
3.1 钢衬里撕裂准则及泄漏理论分析
由于钢衬里撕裂主要发生在刚度不连续区域的局部位置,准确模拟安全壳结构钢衬里撕裂需要建立复杂的分析模型,需要的计算工作量也很大。Dameron 等[33]提出了一种预测钢衬里撕裂的简化分析方法,这种方法以相关试验和精细化数值分析研究得到的安全壳结构典型不连续位置处的钢衬里应变集中数据库为基础(见图6),这些不连续区域主要包括墙体-基础交接面,人员和设备闸门,主蒸汽贯穿件和其他中型贯穿件以及起拱线位置。
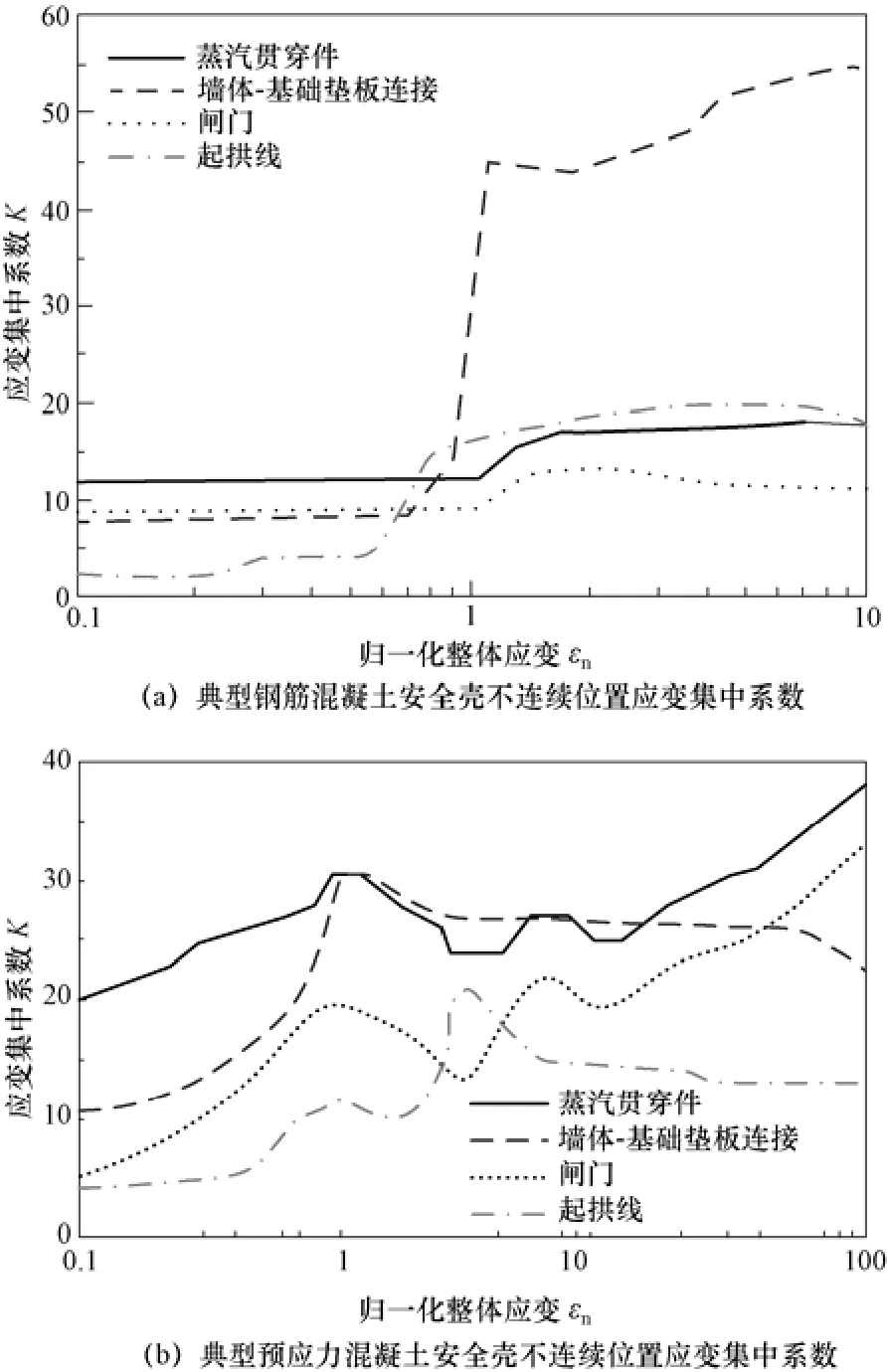
图6 安全壳典型不连续位置处应变集中系数Fig.6 The strain magnification factor of discontinuities for the containment structure
归一化整体应变采用如下的形式:
式中:εglobal——局部峰值应变位置对应的整体应变;
E——钢衬里弹性模量;
σy——钢衬里屈服强度。
Dameron 提出的不连续区域位置处钢衬里撕裂准则采用放大安全壳结构整体应变的方法来考虑,具体采用如下的形式:
式中:εp——不连续位置处的等效峰值单轴应变;
K——应变集中系数;
B——多轴应力状态系数。
式(2)的提出是基于文献[34-36]研究以及钢板双轴应力状态下的断裂试验研究成果。
关于多轴应力状态系数的计算方法主要来源于Manjoine[37]提出多轴应力系数与延性的经验关系(见图7),具体计算理论如下:
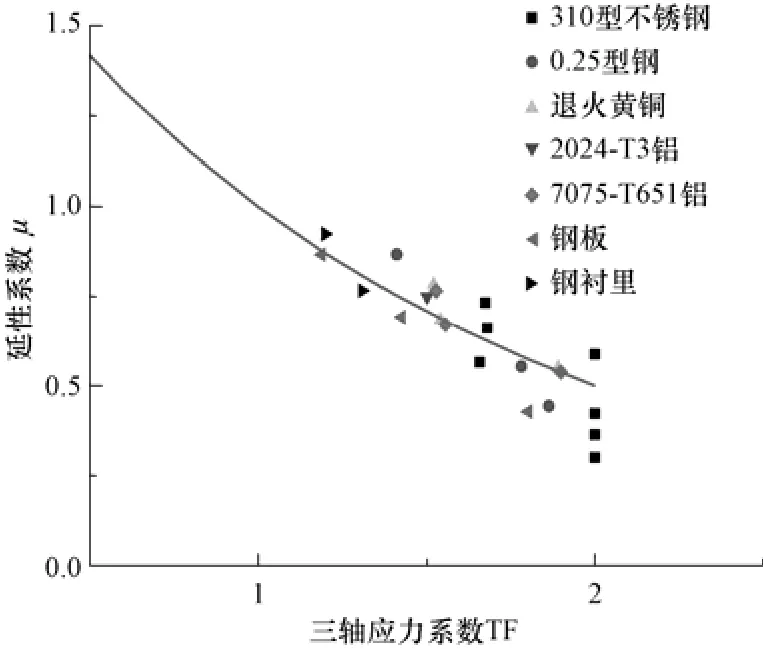
图7 延性系数与多轴应力系数之间关系Fig.7 Relationship between the ductility and the multi-axial factor
式中:μ——延性;
εeff——多轴应力状态下的等效失效应变;
εuniaxial——单轴失效应变。
同时延性μ表达式如下:
式中:TF——Davis 三轴系数,根据文献[38],该系数采用如下的形式:
式中:σ1、σ2和σ3——三个方向上的主应力;并且以拉应力为正,压应力为负。
对于钢衬里这种厚度方向应力较小的部件,可以视为平面应力状态,于是式(5)可以简化成如下的形式:
Spencer[39]在Cherry 和smith 等[40]在考虑锈蚀的安全壳结构性能分析中,不再采用单一的应力集中系数来描述各种因素对钢衬里撕裂的影响。具体表达形式如下:
式中:fm——多轴应力状态系数;
fc——钢衬里考虑锈蚀的影响系数;
fc-u——钢衬里锈蚀影响不确定性系数;
fg——测量长度系数,文献[41]建议取4.0;
fFEM-u——有限元模型不确定性系数;
式中:σ1、σ2和σ3——三个方向的主应力;
σvm——Mises 应力。
同时忽略钢衬里厚度方向的应力即取σ3=0,于是式(8)退化成如下的形式:
Smith 等[43]在展开预应力筋退化情况下的安全壳极限承载力研究时,结合Miller 等[44]研究成果提出了钢衬里撕裂的表达式:
式中:εfailure——有限元计算分析中钢衬里对应的失效应变;
εuniaxial——单轴拉伸试验的失效应变;
fm——多轴应力状态的折减系数;
fm-s——考虑分析模型复杂性的折减系数,Smith 建议[43]取0.2;
fm-v——反映材料性能变异性的折减系数,Smith 建议[43]取0.78;
关于多轴应力状态系数 可以表达为如下的形式:
同样对于平面应力状态问题,多轴应力状态系数fm可简化为:
图8 给出Dameron,Spencer 和Smith 等给出的钢衬里撕裂模型中多轴应力状态系数计算公式在不同应力状态下的比较,从图8 来看,三种计算方法有明显差异,且Smith 提出的多轴应力状态系数与其他两种方法差异很大,在应力比超过1.5 以后,Spencer 方法计算的多轴应力状态系数与Smith 的方法差别较小(见表1)。

表1 多轴应力状态系数比较Table 1 Comparison between the multi-axial stress factors
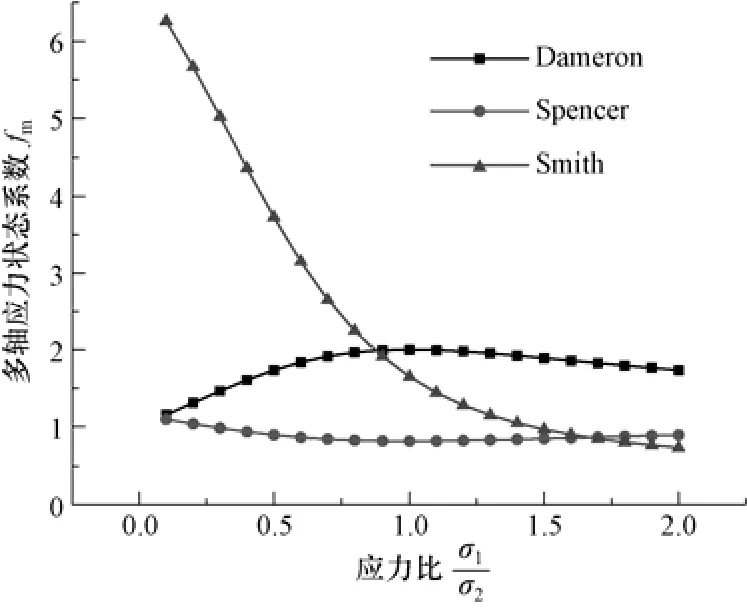
图8 不同应力状态下多轴应力状态系数比较Fig.8 Comparison between multi-axial factors with different stress ratios
Dameron,Spencer 和Smith 三人提出的钢衬里撕裂模型中考虑得不尽完善,因此本文综合Dameron,Spencer 和Smith 等关于钢衬里撕裂准则考虑的影响因素,并建议采用如下的钢衬里撕裂准则:
对于筒体标准段区域的钢衬里有σ1=2σ2,代入式(6)可以得到对应的多轴应变状态系数=0.60;=0.25;=0.20;=0.78。偏于安全,取钢衬里单轴失效应变εuniaxial=20%;于是可得安全壳结构标准段筒体钢衬里在有限元分析中对应的撕裂应变εFEM,failure=0.47%;对于穹顶位置的钢衬里,有σ1=σ2,同样可以计算得到对应安全壳穹顶位置对应多轴应力状态系数为=0.50及钢衬里撕裂失效准则εFEM,failure=0.39%。表2 列出了不同钢衬里撕裂准则的比较结果。将美国核管会的导则RG1.216[45]给出的钢衬里破坏应变视为基准,比较发现本文建议的钢衬里撕裂准则判定方法与基准结果十分接近,而其他钢衬里撕裂判定准则与基准结果相差较大。
Dameron[46]在钢衬里撕裂机理研究工作的基础上,广泛调研和总结研究试验结果,基于泄漏理论计算公式以及经验裂缝公式提出了安全壳泄漏评价方法。钢衬里裂缝宽度平均值可按下式近似计算:
式中:w——钢衬里平均裂缝宽度;
εg——整体应变;
s——锚固件垂直钢衬里裂缝的跨度或间距。
通过钢衬里撕裂的泄漏量可按式(15)计算:
式中:R,T——气体常数;
L——沿着气体泄漏方向的混凝土墙厚度;
B——裂缝长度;
f——无量纲的摩擦系数且k=2.9·107·w1.3;
Re——雷诺数;
Dameron 提出的泄漏量计算原理如图9 所示。
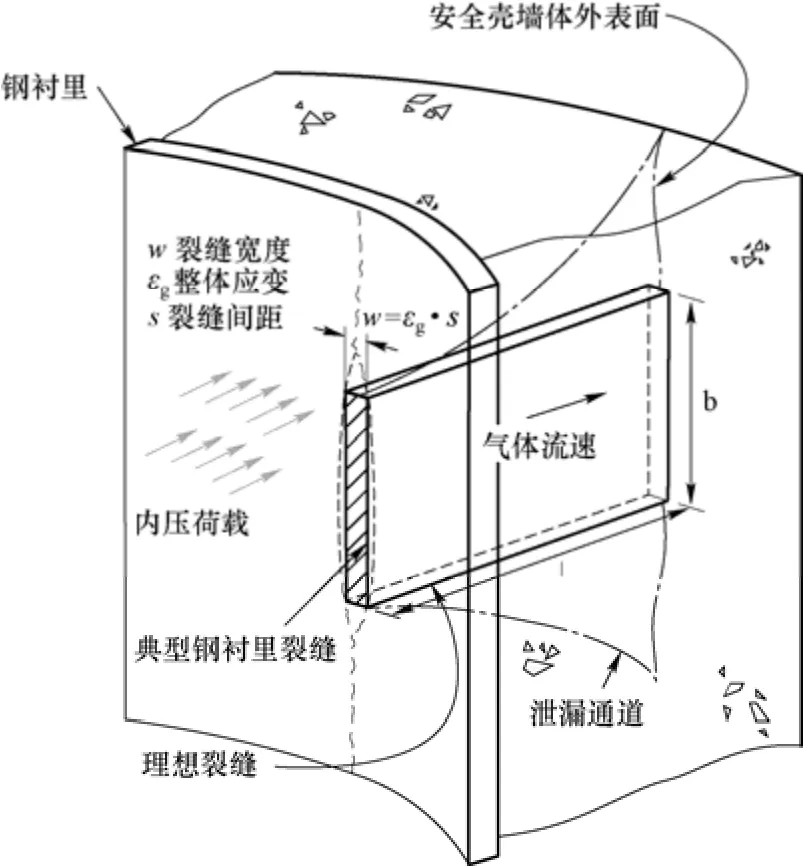
图9 钢衬里撕裂泄漏计算示意Fig.9 The schematic for calculation of the leakage through the liner tear
Tang 等[41]在Dameron 相关研究成果的基础上发展了安全壳结构概率性能评价分析方法,具体概率计算分析理论如下:
式中:K和B——服从对数正态分布的随机变量;
βR和βu——模型计算中相关计算参数的随机性和不确定性。
同时Tang 等[41]也给出了βR和βu建议的经验取值,具体建议值列在表3 中。
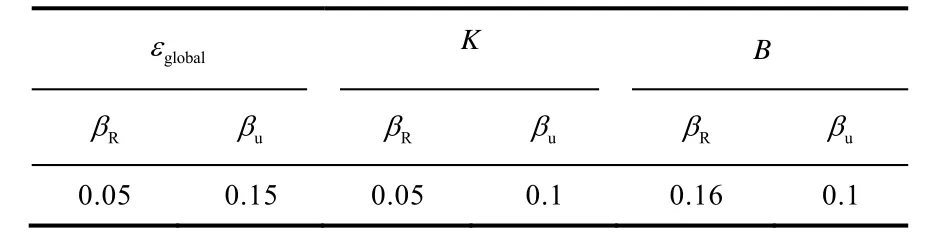
表3 βR和 βu 建议取值Table 3 Suggested value of βR and βu
破裂失效模式主要通过钢衬里撕裂面积来描述。有关钢衬里撕裂面积计算方法具体如下,首先钢衬里撕裂的平均裂缝宽度同样采用式(14)的表达形式;因此钢衬里的撕裂面积表达为如下的形式:
式中:a——钢衬里撕裂的裂缝长度;可以按经验方法取为峰值应力(应变)区域对应的长度、局部区域的特征尺寸或取为沿着裂缝方向栓钉的间距。
因此对整个安全壳而言,总体泄漏面积(钢衬里撕裂面积)可表达为:
式中:Ai——位置i对应钢衬里的撕裂面积;
δi——示性函数,δi=1表示位置i钢衬里发生撕裂,δi=0表示位置i钢衬里没有发生撕裂;
ni——位置i出现裂缝的条数,frupt-u表示计算总泄漏面积的不确定性系数。
如果泄漏面积Atotal超过0.028 m2认为安全壳结构发生破裂失效。灾难性破裂失效模式对应安全壳承载力不采用钢衬里撕裂面积来表达,而是采用下式计算对应承载力:
式 中:σrebar-ult、σliner-ult和σtendon-ult——钢筋、钢衬里和预应力筋的极限强度;
Arebar和Atendon——钢筋和预应力筋面积;
srebar和stendon——钢筋和预应力筋间距;
tliner——钢衬里厚度;
R——安全壳半径;
frupt-u——安全壳结构发生灾难性破坏对应的破坏压力的不确定性系数。
钢衬里撕裂及泄漏计算理论是基于相关试验结果提出的分析方法,这种半经验半理论的分析方法有一定局限性,例如钢衬里撕裂问题中的多轴应力状态系数是基于其他相关金属试验结果得到的经验公式,不完全适用于核电厂安全壳结构中的钢衬里;不同钢衬里撕裂准则计算公式中的多轴应力状态系数有一定差别,同时不同学者提出的钢衬里撕裂准则考虑因素差别较大。此外,影响钢衬里撕裂机理的其他因素诸如焊缝、温度作用目前没有考虑。Dameron 提出的安全壳结构泄漏率计算基于钢衬里撕裂的裂缝宽度经验公式和假设的裂缝长度公式,与实际情况有一定差别。Tang 提出的基于概率框架安全壳结构泄漏性能评价仅给出概率分析方法的雏形,通过简单的不确定性系数来实现,随机性系数和不确定性系数均根据相关经验确定、钢衬里撕裂面积以及泄漏量计算都采用经验公式,后续还需要系统深入理论分析来完善相关理论。
3.2 钢衬里其他力学行为理论分析
关于钢衬里屈曲行为研究,国外学者早期已进行了大量的研究工作。钢衬里屈曲分析计算原理如图10 所示。
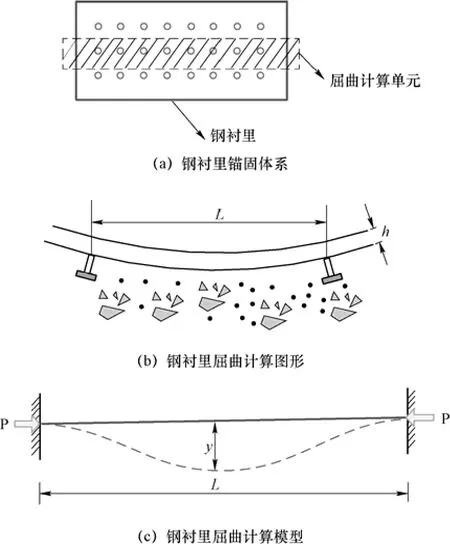
图10 钢衬里屈曲理论分析模型Fig.10 The theoretical analysis model of steel liner bulking
文献[47-49]基于梁单元屈曲理论推导了钢衬里弹性屈曲、弹塑性屈曲的解析解。并在此基础上给出防止钢衬里屈曲的设计方法及钢衬里锚固体系设计方法。
目前这些关于钢衬里屈曲问题的研究为钢衬里的锚固体系设计提供了重要的理论和分析依据。但上述研究主要存在以下缺陷,大多数基于梁单元理论的弹性方法来分析钢衬里屈曲行为,无法考虑钢衬里双向受力状态对钢衬里屈曲行为的影响。
4 总结及展望
本文对安全壳结构钢衬里力学行为研究进行归纳和总结。主要从试验研究、数值模拟及理论分析三方面进行系统分析和阐述,特别对钢衬里撕裂行为的理论模型进行详细深入的对比分析,并且在此基础提出了建议的钢衬里撕裂准则。此外,对其他钢衬里力学行为研究也进行了详细的讨论并指出不足。总体来讲,目前国内在钢衬里力学行为研究领域刚起步,需要加大核电厂安全壳结构钢衬里力学行为研究,尤其需要进一步研究钢衬里撕裂机理,完善安全壳结构泄漏计算方法,并在此基础上发展安全壳结构泄漏性能概率评价方法仍然是今后研究工作关注的重点。
