核动力系统运行工况预判的深度学习方法研究
2023-11-08刘永超谭思超
梁 彪,黄 涛,袁 鹏,刘永超,王 博,*,谭思超
(1.哈尔滨工程大学,黑龙江省核动力装置性能与设备重点实验室,黑龙江 哈尔滨 150001;2.中国核动力设计研究院核反应堆系统设计重点实验室,四川 成都 610213)
核动力系统使用需求与运行环境复杂多样,设计过程中需考虑在长时间运行中可能出现偏离稳态的变工况(正常运行瞬变与事故变工况)运行,传统的核动力系统运行工况判断主要依赖于运行规程、操作人员经验及专家知识。大多数情况下需要变工况发展至一定程度,且相应参数变化至参考阈值后才能进行有效判别。变工况的初始阶段引起的参数微小变化往往很难被有效识别,诊断的及时性与可靠性方面存在欠缺。此外,目前的运行无法做到对系统监测参数变化趋势的超前预测感知。
近年来,基于数据驱动的智能算法辅助核系统运行的研究增多。喻海滔、SHI Xiao-Cheng、颉利东[1-3]等分别使用多层前馈(BP)、径向基(RBF)、卷积(CNN)神经网络模型对核动力装置多类运行工况进行了识别。相比传统的基于树模型[4]等诊断方法,故障诊断的准确率与自适应性得到了提高;宋梅村[5]等基于所选定的15 种热工参数使用BP 神经网络较好地预测了多种故障模式下的船舶反应堆装置功率;张奥鑫[6]等采用某CANDU 重水堆核电厂真实运行数据,使用长短期记忆(LSTM)和CNN 网络有效预测了堆芯短期热功率值;曾聿赟[7]等通过支持向量回归(SVR)训练得到了下一时刻反应堆功率与冷却剂温度的机器学习预测模型。尽管如此,目前相关的反应堆事故诊断研究在判别精度上与工程应用需求尚存在一定差距,同时运行参数预测研究大多局限于单个时间步、某一时刻的单个参数,缺乏对未来长时间内多参数变化趋势的有效预测,算法在实际的工程应用中存在着短板。
基于上述不足,本研究构建了一种基于深度学习的核动力系统运行工况高精度判别与监测参数长时间超前预测的模型,逻辑结构如图1 所示,主要工作内容如下:
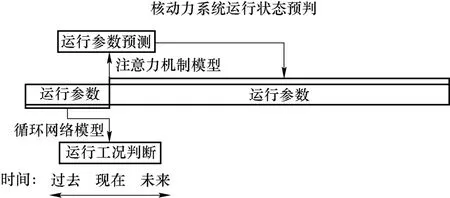
图1 核动力系统运行工况预判模型结构Fig.1 The structure of nuclear power system operation state identification and parameter prediction model
(1)本研究基于改进循环神经网络模型,利用多参数融合方法,使用系统的多个参数的历史变化趋势来综合判断运行工况,而不是使用单一时刻的参数,大幅提高了运行工况判别的准确率;
(2)为提高模型对工况类型的判别精度,使用自动化的网格搜索算法(Grid Search)调整优化工况判别模型的结构参数,而不是依赖于小区间范围内的人工试验与经验选择;
(3)本研究基于改进的注意力机制模型实现了对核动力系统参数变化趋势的长时间、多参数的有效并行预测。
1 特征选择
1.1 数据集介绍
核动力系统运行数据来源于全范围核动力仿真机计算[8],共包含10 种类型的运行工况从开始至结束记录的24 个热工水力参数变化,具体如表1 所示。

表1 数据集参数说明Table 1 Data set parameters
1.2 数据特征选择
为了寻找工况判别模型的最优特征子集,剔除数据集中的冗余特征,降低模型复杂度、避免训练中的过拟合风险,搭建神经网络模型前数据预处理中需进行特征选择。可以描述为:假设N个特征组成集合XN={Xi},依据目标函数F,选取特征子集Y,使得F(Y) ≥F(T),T为X的任意子集。特征选择的方法主要有封装器法、过滤器法和嵌入法。首先利用皮尔逊系数(Pearson)对特征进行过滤。Pearson 系数用于度量两个变量之间的相关程度,介于 -1与1 之间,计算见式(1),绘制计算结果如图2所示。
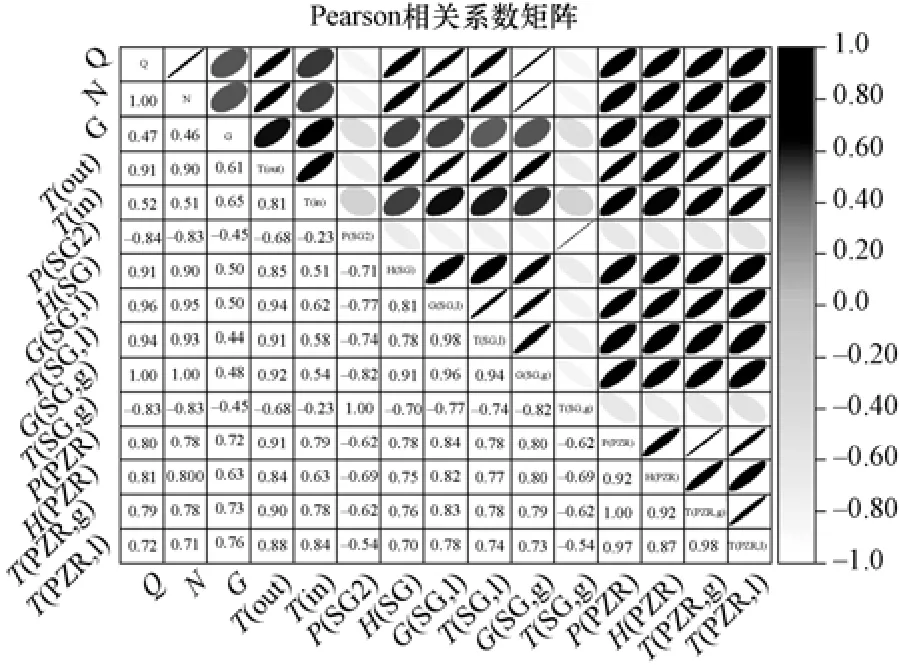
图2 数据集原始特征相关性分析Fig.2 The correlation analysis of the data set original features
从图2 可以看出,热功率与电功率、SG 蒸汽出口流量三个特征之间彼此的Pearson 值均为1,有着强烈的线性关系,故仅保留热功率特征;SG 出口蒸汽温度与二次侧压力的相关系数为1,舍去SG 蒸汽出口温度特征。
之后利用封装器法对特征的重要性进行简单评估,随机森林利用随机重采样技术(Bootstrap Aggregating),采用抽放放回的方法选择n(n<N,N为样本总数)个样本作为训练集数据基于CART 算法构建k棵决策树。假设特征X j的基于分类准确率的变量重要性度量为,使用袋外数据(OOB)方法计算,基于决策树模型的随机森林集成算法对不同特征的重要性进行排序[9],算法结构如表2 所示,计算结果如图3 所示。

表2 特征重要性排序算法结构Table 2 The structure of feature importance ranking algorithm
特征Xj的特征重要性度量的计算公式为式(2),对应特征加入随机噪声后,OOB 数据的准确率下降越明显,则该值越大,表明该特征对模型的影响很大,其重要性更高。
从图3 中可以看出,不存在重要性度量指标明显过小的特征,为保证判别模型对工况的识别精度尽可能高,对剩余特征不再舍去。
2 运行工况判别
核动力装置系统复杂,监测变量多,各个运行工况下启停阶段热工参数的差异并不明显,因此不同工况下的数据映射在张量空间中无法避免地分布紧密或存在交集,传统的支持向量机(SVM)、决策树(RF)、贝叶斯(NBM)、BP 网络等由于算法设计的限制,只能处理一维数据,因此其对运行工况的判别只能采用某一时刻的运行数据,针对复杂数据集在理论上无法达到较高的识别准确率。
为了克服上述问题,本研究基于能够有效提取运行数据时间维度信息的LSTM(改进循环网络)模型从根本上克服传统算法单点诊断的弊端,利用多参数的时序趋势进行工况判断。LSTM 模型通过引入状态变量存储过去一段时间内的热工参数变化趋势信息,并用其与当前时刻的参数共同决定当前的运行工况状态输出。
式中:模型的W与b为同一套权重与偏置矩阵,通过梯度下降法迭代更新。
LSTM 模型内部节点的计算结构如图4 所示,当前t时刻的热工参数Xt与输出tY的计算如式(3)所示。核动力系统运行工况判断模型的结构如图5 所示,其由一层LSTM 层与两层前馈层构成,该模型输入的数据为三维张量[batch_size,seq_len,features_nums],三个维度分别表示数据批次大小、时间序列长度与运行参数,取LSTM 层输出的最后一个时刻的参数传至前馈层,经两层前馈层与sigmoid 激活函数非线性映射后,输出的数据形状为[batch_size,kinds_nums],第二个维度表示工况的类别数,再经过softmax 函数转化为概率分布。训练使用one-hot 编码将离散标签的均匀等距地扩展到向量空间,损失函数使用交叉熵。
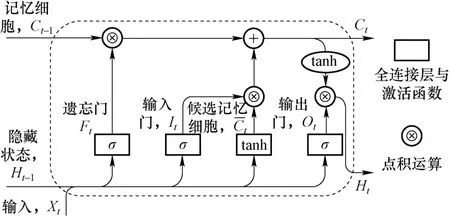
图4 LSTM 网络内部节点计算过程Fig.4 The calculation process of internal nodes in the LSTM network
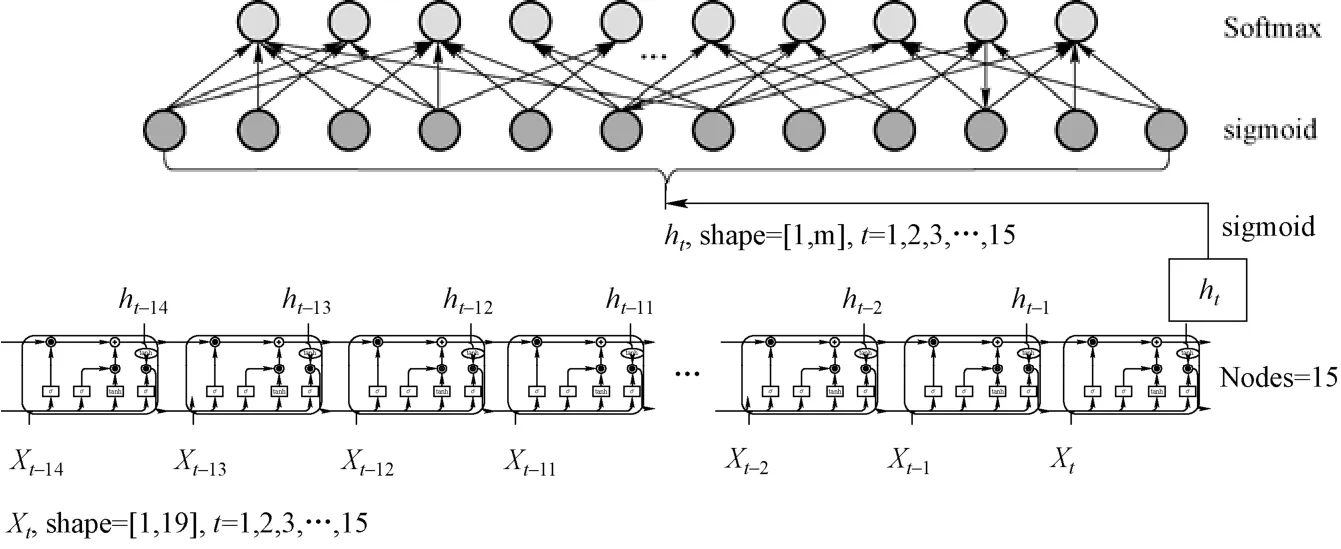
图5 核动力系统运行工况判别模型结构Fig.5 The structure of operating condition identification model for nuclear power system
为了提高模型判别工况的准确率,首先对模型输入选择的不同时间步长下的识别结果进行比较,结果如图6 所示,最终选择LSTM 层输入的时间序列长度seq_len=15。

图6 模型输入时间步长搜索结果Fig.6 Search results of different model input time steps
之后对判别模型的内部结构进行优化,常见的方法有网格搜索、随机搜索与贝叶斯优化,后两种方法对比网格搜索在计算速度方面占有优势,但无法取得最优结果,故采用网格搜索算法在指定的参数范围内,对LSTM 层的隐藏层节点与中间前馈层节点数进行搜索,搜索空间共包含225 种网络结构,得到的搜索结果如图7 所示,最终选择模型网络中间两层的节点数分别为22 与21,优化前后模型对运行工况的判别准确率由0.90 提高至了0.99 以上。
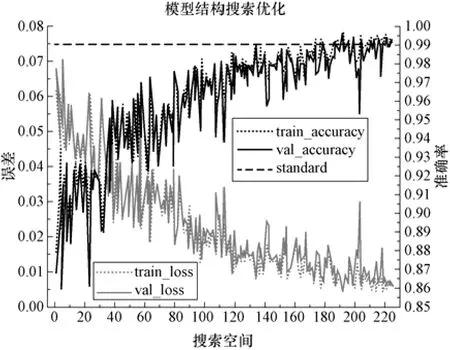
图7 模型结构搜索结果Fig.7 Search results of different model structures
训练完成后,对于新输入数据,模型计算时间在毫秒级,测试工况上的判别输出结果与真实结果对比展示如图8 所示,工况类型1~10 如表1 所示。可以看出建立的模型对运行工况识别的准确率获得了较大的提升。极小部分的判别错误集中于各运行工况开始发生的极短时间内,主要是由于各种运行工况在最初发展阶段的运行参数差异过小造成的。

图8 运行工况判别模型诊断结果混淆矩阵Fig.8 The output confusion matrix of the operation condition identification model
几种经典算法对相同测试工况的识别结果比较如表3 所示,同时考虑到核动力系统实际运行中监测系统的传感器不可避免地会产生随机测量误差,对测试数据引入随机噪声,表3展示了各个模型的工况判别准确率并未由于噪声数据引入而显著降低,表明了深度学习模型在工况判别中良好的泛化能力。
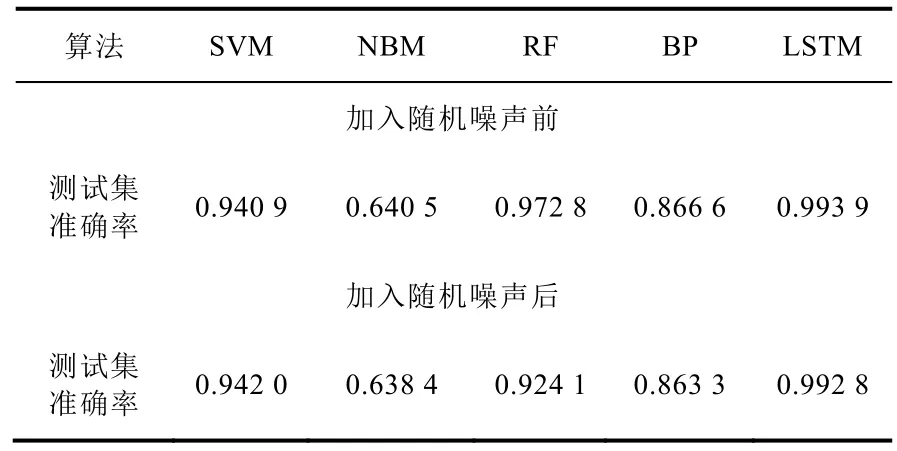
表3 不同模型对运行工况判别的准确率Table 3 The accuracy of different models in distinguishing
3 热工参数预测
以历史运行数据预测未来运行参数变化是序列数据预测(Sequence Prediction)问题。常用的循环神经网络(RNN)随着时间长度的增加,训练过程中梯度累计爆炸或消失[10]导致无法使用。本研究基于完全注意力机制(Transformer)模型对参数变化趋势进行预测,解决核动力系统运行参数变化趋势长时间捕捉的超前感知问题。
Transformer 模型的核心在于计算注意力[11](Attention),如式(4)所示,模型的整体结构由编码-解码器(Encoder-Decoder)两部分[12]组成,在键张量(key,K),值张量(value,V)中引入查询张量(query,Q),计算过程为使用Q张量计算它和每个K点积的相似度作为权重,对所有的V进行加权求和,防止点积计算结果过大导致梯度消失。解码器选择性地获得编码器的隐藏状态信息。对比RNN 类模型,针对时序信息,Transformer 类模型在时间维度上解决了学习长期依赖性的挑战。
式中:X——运行时序数据;
WK,WQ,WV——权重张量,在训练过程中迭代;
d——特征列数。
针对长时序数据处理问题对模型做出了部分改进[13]。为了减小参数量,避免训练过拟合,通过在网络内部层之间叠加由一维卷积层与最大池化层组成的Distilling 模块对时间序列的时间维度长度进行降维,提取长时间序列输入数据的特征,如式(5)。
循环网络类预测模型是动态输出的,过去时刻的输出作为当前时刻的输入,按步迭代,依次向前滚动预测;本研究预测模型采用待预测序列之前的一个序列一步直接生成所有的预测结果[14],避免了RNN 类模型的预测误差累积,同时加快了预测速度。
运行参数预测模型结构及数据维度的变化如图9 所示,Encoder 的子模块之间采用串联计算,其内部多个注意力模块同时并行计算,增大模型宽度;时间序列数据输入到Encoder 与Decoder 前都需经过embedding 编码操作,由输入数据自身编码、对应时间序列([日,时,分,秒])编码及位置编码三部分相加构成,由于预测模型中数据一起并行计算,丢失了时序信息,所以对数据必须进行位置编码,如式(6)所示。同时,区别于Encoder 输入,Decoder 的输入数据中的被预测部分X0需用0 替换覆盖,即mask 操作。Attention 层计算后通过使用网络的残差连接结构与每一个样本上的归一化操作,解决训练过程中由于多层堆叠造成的梯度消失问题。Decoder 同时接收自身mask 后的数据与Encoder 的输出,Decoder 运算后再经前馈层映射一步输出结果,损失函数为均方误差。
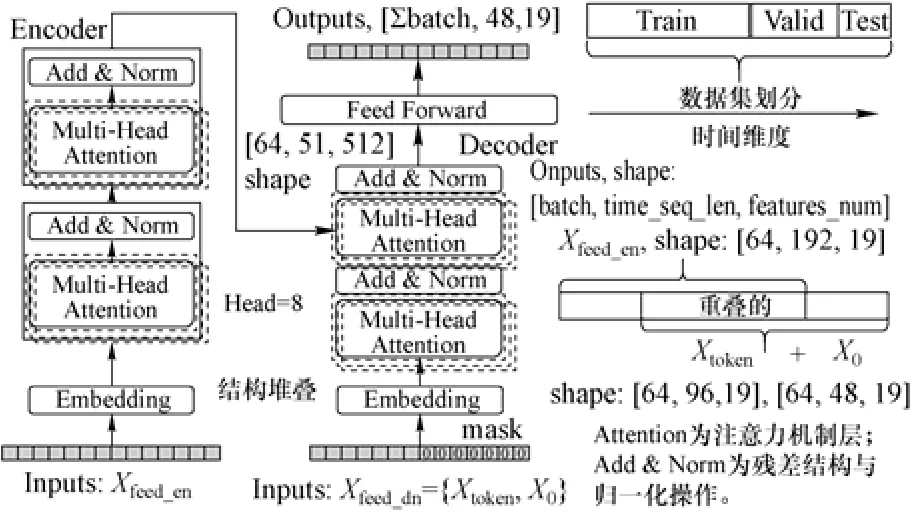
图9 参数预测模型结构Fig.9 The structure of the parameter prediction model
式中:pos——序列中的位置编号;
dmodel——位置向量的维度,数值为512。
以预测SGTR 事故为例,冷却剂由传热管破口位置流向二回路侧,稳压器水位与压力降低补偿一回路的压力损失。选取事故进行中的时刻T0与T1,使用过去192 与384 个时间步的历史数据预测之后稳压器压力48 与96 个时间步内的变化趋势,多种模型计算用时均在毫秒级,超前预测的标准化结果对比如图10 与图11 所示。
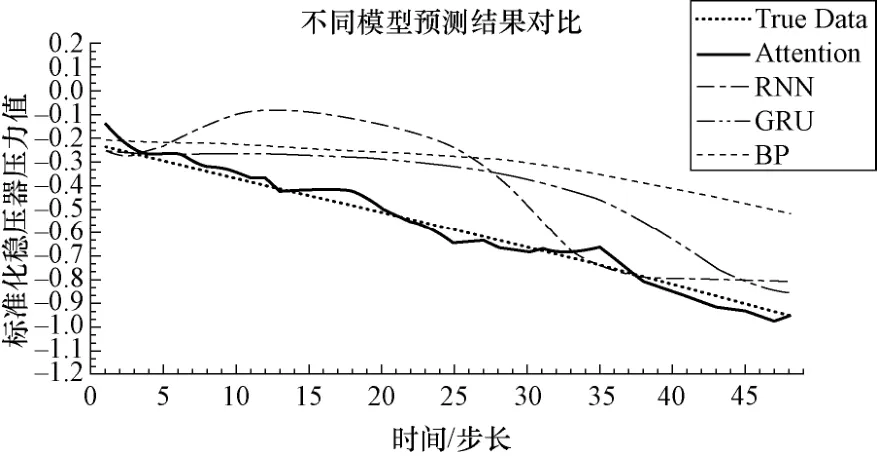
图10 T0 时刻预测48 个采样步长的稳压器压力变化Fig.10 The pressure change of regulator with 48 sampling steps predicted at T0

图11 T1 时刻预测96 个采样步长的稳压器压力变化Fig.11 The pressure change of regulator with 96 sampling steps predicted at T1
对比分析可知,RNN、GRU 等几种循环神经网络,在初始的5 个采样步长内对稳压器压力的预测精度较高,但对于长时间序列下的热工参数变化趋势无法预测;BP 网络能够粗略预测长时间序列下的变化趋势,但由于模型的动态输出机制导致误差不断累加,整体的预测误差很大;注意力机制模型可以较为准确地预测稳压器压力的长期变化趋势,在比较的几种模型中效果最好。
由于不同工况下的进程和事故序列不同,选择另外几种运行工况发展下的预测继续验证模型。由图12 所示,基于数据驱动的神经网络模型能够很好学习到数据的统计分布规律,对不同的运行工况依然适用,泛化性很好。由于受所使用训练数据集的影响,在准确捕捉变化趋势的前提下,预测结果出现极值小波动问题还存在不足,需进一步改进模型与实验对比观测。
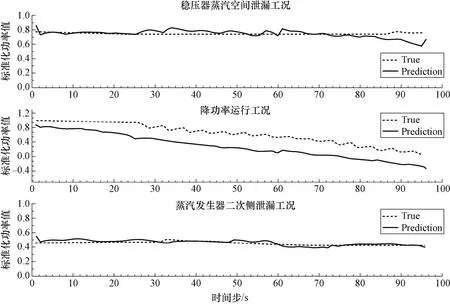
图12 几种不同的运行工况下堆芯热功率值预测Fig.12 The core thermal power prediction under several different operating conditions
4 结论
本研究提供了一种基于数据驱动的运行工况实时识别与超实时感知的通用方法。在通过特征选择实现数据降维的基础上,两种模型的计算时间均在毫秒数量级,满足工程应用中实时判别与预测的要求,可为运行人员提供全流程的运行工况识别辅助与运行参数变化趋势超前感知,降低人因失误概率,为核动力系统的自主运行与控制技术提供参考。本研究的进一步工作方向主要为算法的集成开发。
