面向乳腺癌诊断的压电式微机械超声换能器的设计*

刘 畅，程义军，薛晨阳，张斌珍

(1.太原工业学院电子工程系，山西 太原 030008；2.中北大学仪器科学与动态测试教育部重点实验室，山西 太原 030051)

依据世界卫生组织癌症研究中心统计数据，女性乳腺癌的患病率为30.1%，发病率为24.2%，死亡率为15%[1-2]。 因此，为提高乳腺癌患者存活率，早期精确诊断至关重要[3]。 随着超声CT 技术的快速发展，其有望成为用于乳腺癌诊断的最具潜力的影像学手段。 目前，国内外的部分研究团队一直致力于研究开发用于乳腺癌早期筛查的超声CT 系统，虽取得很大的进步，但仍有很多技术难点需要攻克，研制系统采用的传统压电陶瓷超声换能器就是其中之一[4]。 这通常被认为是进一步创新的最大障碍。尽管取得了令人惊叹的机电耦合成就，但基于先进材料的传感器生产仍然依赖于同样具有挑战性的制造工艺，这限制了元件的小型化，并对图像分辨率、探头尺寸和生产成本产生不利影响[5-7]。

下一代医疗超声系统的实现需要大量、廉价的高效和高灵敏度传感器的制造。 作为一种替代方案，基于微机电系统(MEMS)的设计在大量小型化元件的成本效益制造和利用创新驱动的传感机制提高性能方面显示出了希望[8-9]。 在高声功率方面，与其他MEMS 转换机制相比，压电具有更大的能量密度，这使得压电式微加工超声换能器(PMUT)成为MEMS 基础上的替代方案，可用于更大深度的高分辨率成像[10-11]。

尽管前景看好，但低机电耦合和带宽导致之前研究的PMUT 未能达到预期。 此外，尽管PMUT 研究取得了一些成就，但在对PMUT 性能的基本理解方面，特别是在声压、带宽和机电转换效率方面，仍然存在重大差距，这主要是由于现有的分析模型很少造成的[12-13]。 然而，设计在很大程度上仍然依赖于有限元仿真分析的结果。 通过设计更好的预测模型，专注于对关键性能指标的基本理解，可以在PMUT 设计中使用条理化流程，使实质性的性能改进成为可能，并进一步推动PMUT 技术更接近商业实施。

1 面向乳腺癌诊断的圆形双晶片PMUT 模型结构及工作原理

针对乳腺软组织的特殊性，本课题组开发了图1 所示的基于PMUT 线阵柱形运动的乳腺超声CT系统。 该系统最大的特点是利用二维的结构获取三维的组织信号。 四个垂直交叉的PMUT 配置方案，可以同时获取乳腺组织的反射超声信号和透射超声信号。 进而对超声信号中声速、声衰减和声阻抗等特征参数进行提取，利用多参数融合成像算法完成高分辨率图像重建[2-3]。 PMUT 作为乳腺超声CT系统的核心探测部件，其性能的优劣直接影响乳腺癌早期精确诊断的高特异性。

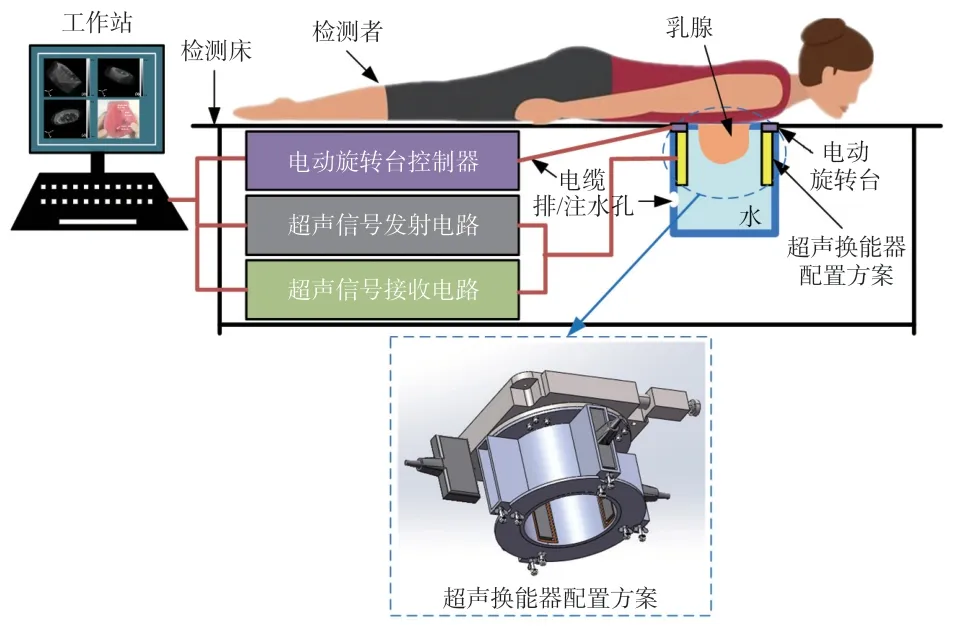
图1 乳腺超声CT 系统示意图

本文所研究的圆形双晶片PMUT 敏感单元结构如图2 所示。 器件分为两大部分:移动的传感层和支撑的衬底层。 上层的移动传感层主要起到声电转换的作用，主要由上电极Mo、压电层AlN，下电极Mo，以及振动层Si 组成的；下层的支撑衬底层主要起到支撑固定的作用，主要由隔离层SiO2和支撑层Si 组成的。 由于AlN 压电薄膜具有较低的介电常数、声匹配性好、易与CMOS 工艺集成等优势，使得PMUT 的设计更具有潜在的医学应用优势。 金属电极存在于压电薄膜的上下表面，选择具有较低电阻率的金属材料Mo，其声阻抗相对于AlN 材料较高，在器件结构相同的条件下，Mo 材料具有较低的电阻，使得器件的品质因数最高，材料的损耗较低。 最后选择性价比较高且导电性较好的Al 材料作为焊接电极引出来，做为测试端。 薄膜材料是PMUT 设计的一个关键方面，应该根据器件性能和制造方法来选择。 尺寸和材料特性决定了薄膜的声学行为。

图2 PMUT 敏感单元结构

PMUT 在接收模式下工作时，用于探测乳腺软组织的超声信号。 在接收模式下，入射压力使压电传感膜片偏转，产生横向应力，并由于压电效应在压电层表面产生电荷。 当入射声波施加于敏感单元表面时，传感膜片向上和向下弯曲。 传感膜片的内部受到压应力，而外部受到拉应力，反之亦然。 压电薄膜由于直接压电效应会在薄膜表面产生正负电荷。为了提高传感器的接收灵敏度，顶部电极应尽可能覆盖没有电荷或应力符号变化的区域。 优化的顶电极特征尺寸通常是传感膜片尺寸的0.7 倍[14]。

2 圆形双晶片PMUT 模型分析

将压电薄膜的边界条件看作简支边界，也就是边界可以弯曲但不可以移动。 边界处的挠度w为零，弯矩Mr为零，数学表达式为[15-16]:

对于简化模型，在均匀压力p的作用下，圆形薄膜上与圆心相距为r处的挠度为:

式中:a为薄膜半径，De为薄膜等效弯曲刚度。

相应的压电层径向和切向的应力，得到如下关系式[17-18]:

式中:Ee和ve为薄膜等效的杨氏模量和等效的泊松比，zp为压电层中心到中性偏转轴的距离。

将式(2)代入式(3)和式(4)中，进一步得到如下关系式:

在假定的理想状态下，压电效应完全来源于某点处的由于压强p的存在而产生的挠度，相应地全部转化成电荷，这时该点处的应力值为零，即径向应力和切向应力值和为零。 通过计算可以发现，当r近似于0.7a时，总压力的理论值为零，因此在此处应该设计为上电极边缘位置。

由于压电效应和逆压电效应的过程是完全互逆的。 因此，当上电极半径与下电极半径的比值为0.7时，不管PMUT 工作在发射状态，还是工作在接收状态，此时的机电转换效率最高，性能最优。

PMUT 的接收灵敏度S可以通过计算如下公式得到[19]:

式中:Ae为上电极的面积，d31和ε分别为压电薄膜的压电常数和介电常数。 当r＝a/2 时，接收灵敏度S可以修改为:

在空气中工作的PMUT 谐振频率可以表示为:

式中:特征尺寸d为圆形薄膜的直径。t是薄膜的厚度。Eeq、ρeq、νeq分别为等效弹性模量、等效密度和等效泊松比。λ01＝40.8，为圆形薄膜的校正系数。当换能器浸入水中时，其谐振频率可以修改为:

式中:ρwater是水的密度。

3 COMSOL 仿真分析

面向乳腺癌诊断的问题，利用有限元仿真软件COMSOL 对所提出的PMUT 进行性能分析验证。 首先，下层的固定支撑层对薄膜移动的效果影响相对较小，因此通过在边界上施加固定约束条件来模拟仿真支撑效果；其次，粘附层对薄膜的机电行为没有贡献，COMSOL 默认假定层与层之间具有完美的粘合。 因此可以忽略粘接层厚度；最后，PMUT 器件是以薄膜厚度方向为中心轴的对称结构，因此在建立仿真模型时可以利用旋转半截面实现整个模型，这样大大简化了计算，在保证器件仿真精确度的同时又能够大幅度减少仿真所需时间，提高仿真的运行效率。

超声信号在乳腺软组织传输中存在衰减问题，并且信号强弱与探测深度呈反比。 一般情况下，软组织的衰减系数为0.6 dB/cm/MHz~0.7 dB/cm/MHz。 依据乳腺组织的立体精准检测需求，所需要的探测深度为18 cm，才能获取较为完备的垂直切片数据。 因此通常在理论上超声换能器工作频率不应高于3.5 MHz，否则会影响到检测深度，所设计的PMUT 敏感单元所用到的关键结构参数，如表1 所示。

仿真模拟中不同结构层材料的性能如表2所示[9]。

表2 仿真模拟中所使用的材料性能

3.1 静态压力和位移分析

当输入大小为1 Pa 的均匀声压作用在器件PMUT 的上表面时，薄膜的压力和位移分布如图3所示。 压电层内的应力从中心向边缘逐渐变化，中心处受到压应力表现为正值，而边缘处受到拉应力表现为负值。 并且在中心处的应力值为35.68 N/m2，在边缘处的压力值为-39.05 N/m2，如图3(a) 所示。 静态位移在中心处达到最大值0.044，其变化从中心向边缘逐渐减小，直到为0 μm，如图3(b)所示。 与式(2)的理论计算值相符合。

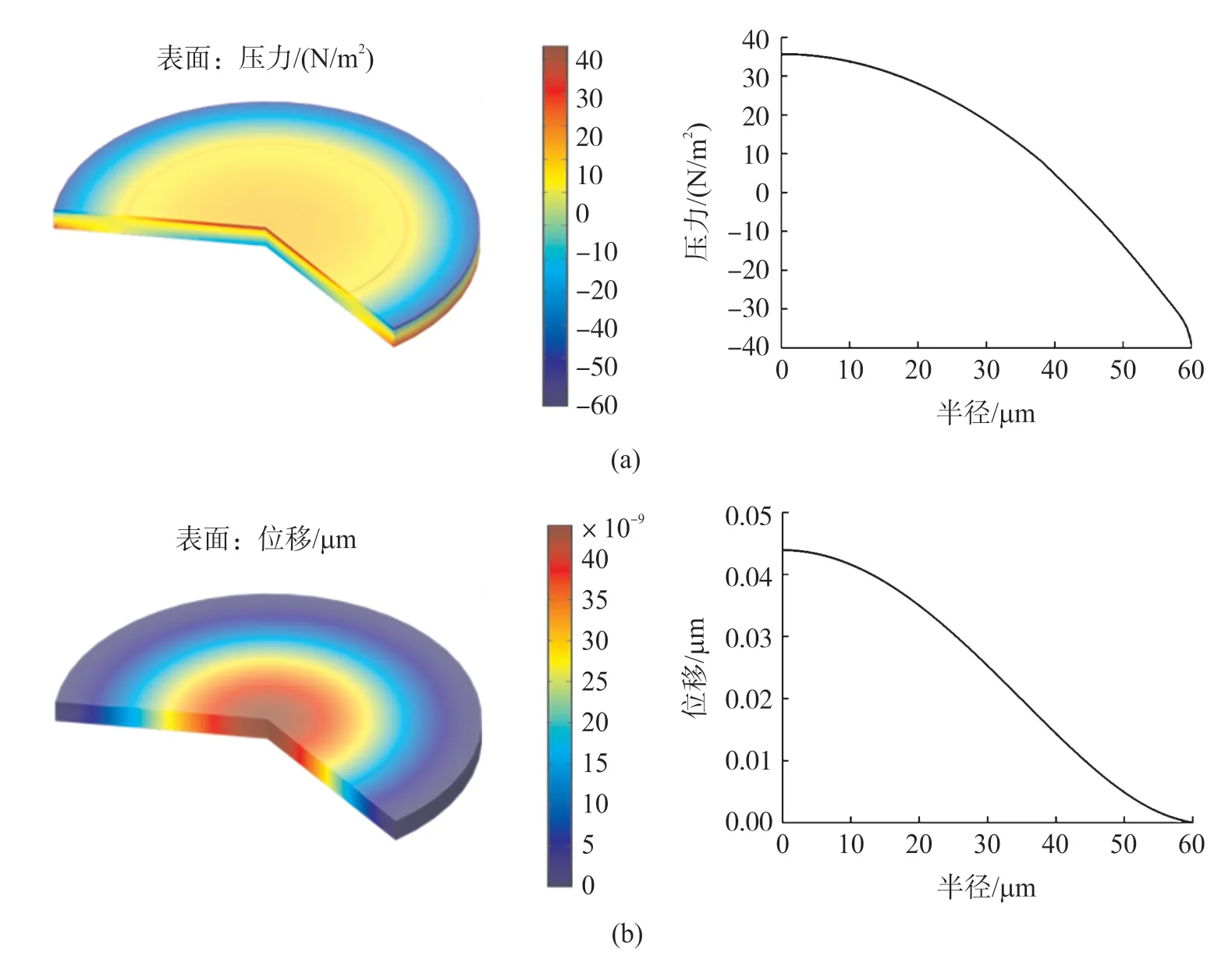
图3 在1 Pa 均匀声压下的薄膜压力和位移分布

3.2 模态分析

进一步地对所提出的敏感单元结构的模态振型进行了有限元模拟。 结构的振动特性可以通过模态分析来实现，根据结构和材料等因素来确定振动模式和固有频率。 边界条件为一端自由，另一端固定的情况下，得到图4 所示器件的前6 阶谐振模态，其所对应的固有频率分别为7.61 MHz、27.69 MHz、56.65 MHz、91.07 MHz、93.44 MHz、128.99 MHz。 随着模态阶数的增大，薄板中间出现了越来越多的驻点，这会导致纵向谐振位移的减小和能量转换效率的降低。 因此，在一阶模态或基频处，振动是轴对称的，且振幅最大，这使得基频模态驱动非常适合超声转导应用。

图4 前六阶谐振模态

对于圆形薄板，挠度剖面与每个模态振型的一个常数有关，该常数是由边界条件数值确定的。模态振型常数是偏转方程的一部分，决定了谐振频率。 通常，设计时需要的振动模式设计为一阶模态，式(9)中将常数指定为λ01，其中01 表示一阶模态。

3.3 谐振频率分析

确定了器件工作在一阶模态下，进一步分析谐波响应。 依据一阶模态固有频率的结果，设置仿真时的频率范围为6 MHz~9 MHz，扫描间隔为1 kHz获取圆形薄板中心节点处的器件振动的位移量，从而得到图5 所示的结果。 谐振频率fr为7.61 MHz，可以看出在谐振频率处，器件的振幅达到最大，最大位移为34.2 μm。

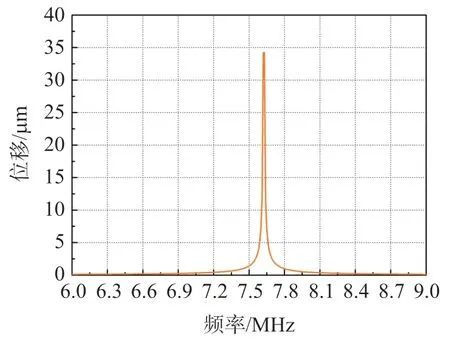
图5 谐振频率分析

膜的变形主要由膜的抗弯刚度决定，利用有限元模型对器件模型的预测进行了细化，理解控制这种变形的物理原理可以指导薄膜和腔体的设计。

3.4 灵敏度分析

PMUT 自由场电压接收灵敏度Me是换能器输出的开路电压Voc与换能器所在位置处自由压强P比值的分贝形式，即

在COMSOL 中利用式(1)可以得到该器件的灵敏度，如图6 所示，其灵敏度的仿真值为-258 dB。

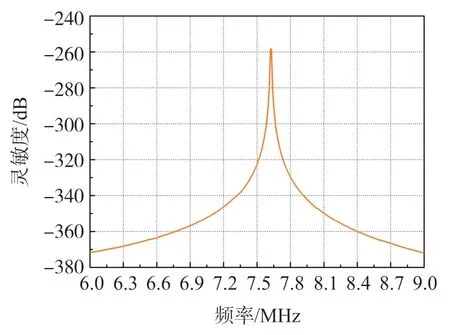
图6 灵敏度分析

从图中可以看出，谐振点前的半功率点频率f1为7.60 MHz，谐振点后的半功率点频率f2为7.62 MHz，根据式(12)计算得到的品质因数Qm为380.5。

式中:f1和f2为半功率点，Qm为机械品质因数，越高越好。

3.6 阻抗分析

机电耦合系数由于定义最为一致，因此可以被用来比较各种PMUT 设计。 图7 为器件的阻抗-频率响应曲线，谐振频率fr为7.61 MHz，反谐振频率fa为7.65 MHz，根据式(13)计算得到的有效机械耦合系数Keff为10.2%。

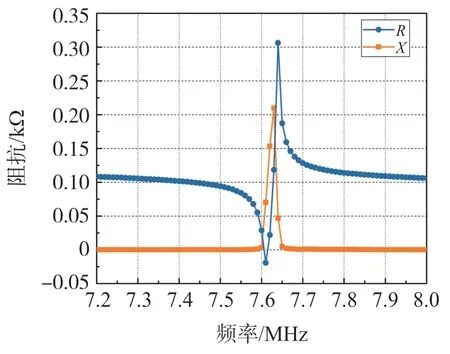
图7 阻抗-频率响应曲线

式中:fa为反谐振频率，fr为谐振频率。

图8 为阻抗的模值曲线，从图中可以看出谐振时最小的阻抗值为35 Ω，反谐振时最大的阻抗值为310 Ω。

图8 阻抗的模值曲线

利用有限元模型来确定可以实现最大的机电耦合系数，并通过阻抗分析来进行阻抗匹配设计，用以指导器件的优化设计，来实现最优的性能。

4 结论

本文围绕着一种基于AlN 薄膜的圆形双晶片PMUT 设计方案，给出了具体的结构参数，并利用COMSOL 进行了仿真验证。 其在空气中的谐振频率为7.61 MHz，与理论计算值7.5 MHz 基本一致，验证了理论模型分析的正确性。 进而可以推算出在水中的谐振频率大约在3.5 MHz 左右，这也间接证明了能够满足对乳腺软组织检测需求。 同时所设计的PMUT 在满足中心频率为7.5 MHz 的基础上，机电耦合效率可以达到10.2%，优于Zhang 等所设计的高频PMUT，其传感器中心频率为7.43 MHz，机电耦合系数为2.21%[20]。 所涉利用有限元分析的方法，以谐振频率为核心参数，结合静态性能分析和动态性能分析，用以指导超声换能器的设计。 为后续压电式微机械超声换能器的实用化进程提供一定的研究基础。