基于Taguchi 法的拉深成形工艺参数优化
2023-11-07魏良庆重庆科创职业学院智能制造学院
文/魏良庆·重庆科创职业学院智能制造学院
拉深作为一种塑性成形工艺,广泛应用于金属成形行业。凸凹模圆角半径、冲压速度、拉深间隙、模具导向方式等工艺参数都会影响拉深产品质量。通过有限元软件ABAQUS 建立了成形件1/4 几何分析模型,结合Taguchi 法,分析了凸模圆角半径、凹模圆角半径和冲压速度对拉深件9 个位置的等效应力和等效应变的影响。结果表明,凸模圆角半径对等效应力分布的影响最大,对冲压速度的影响最小。对等效应变分布的影响从大到小依次为凹模圆角半径、凸模圆角半径、冲压速度。最大等效应力主要集中在凸缘部位和凸模圆角处,最大等效应变主要分布在凸模圆角处、筒壁和底部区域。
拉深是金属板料的一种重要成形工艺,广泛应用于汽车、航空航天、电子元件、仪器仪表等领域。在拉深过程中,毛坯通过塑性变形获得所需形状。拉深变形过程非常复杂,是一种典型的非线性问题,不仅包含材料非线性问题,还涉及几何非线性和接触非线性问题。此外,在拉深过程中极易产生一些缺陷,如变薄、起皱、拉裂和表面划痕等。因此,有必要对拉深工艺参数进行优化,以保证产品质量。本研究基于Taguchi 法和ABAQUS 有限元分析软件,分析了凸模圆角半径、凹模圆角半径、冲压速度等工艺参数对拉深过程中等效应力和等效应变的影响。
模型建立
拉深过程中的几何参数如表1 所示。在拉深过程中,将凸模、凹模和压边圈视为刚体,毛坯(304 不锈钢)视为弹塑性变形体。由于该产品属于简单的轴对称拉深件,摩擦系数可以取常数,设置为0.18。
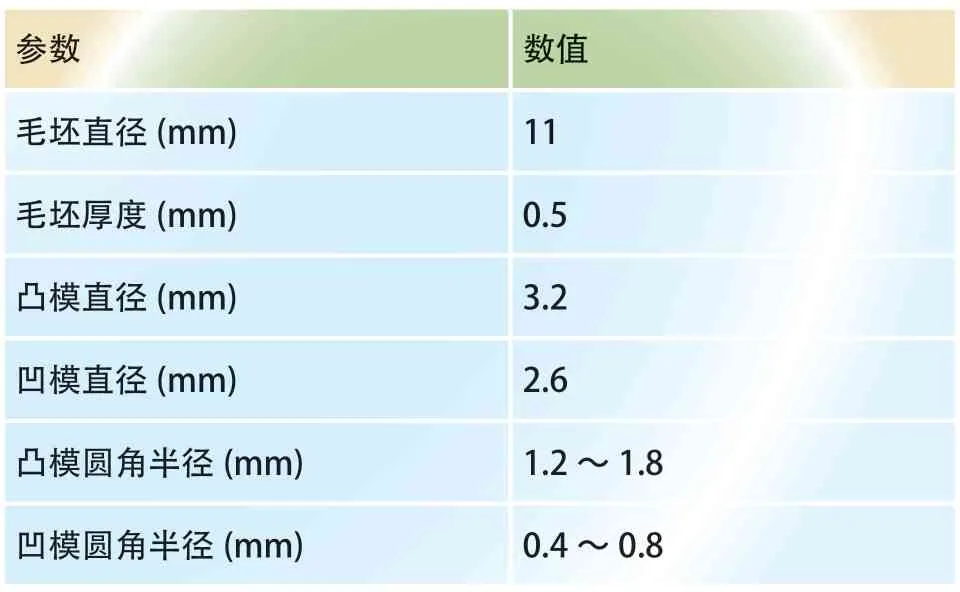
表1 拉深过程中的几何参数
在板厚为2mm、冲压速度为5mm/s 的条件下进行了单向拉深试验,304 不锈钢性能参数如表2所示。
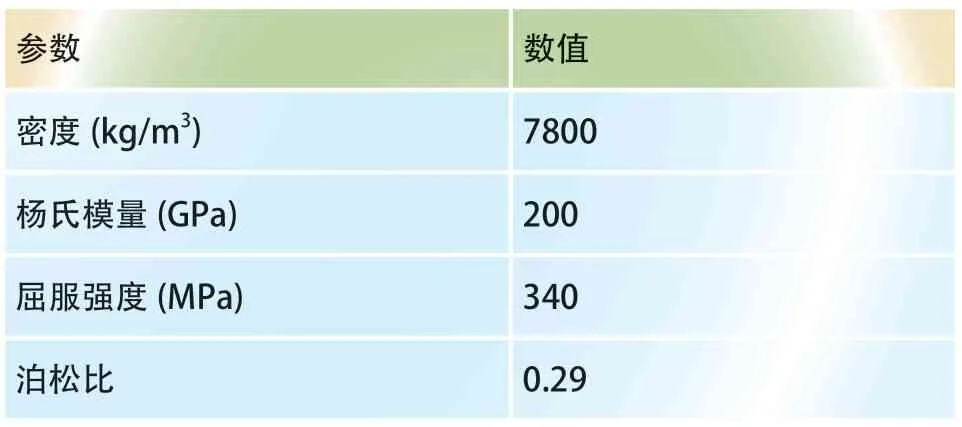
表2 毛坯性能参数
利用ABAQUS 软件可以解决非线性材料问题和具有塑性变形的几何非线性问题。为了加快计算速度,只建立了毛坯的1/4 几何模型。毛坯采用C3D4 实体单元,共计1824 个单元,如图1 所示。凸模、凹模和压边圈均采用R3D4 实体单元,共计3024 个单元。整个仿真模型共有4848 个单元和6018 个节点。惯性力忽略不计,模型为准静态的。
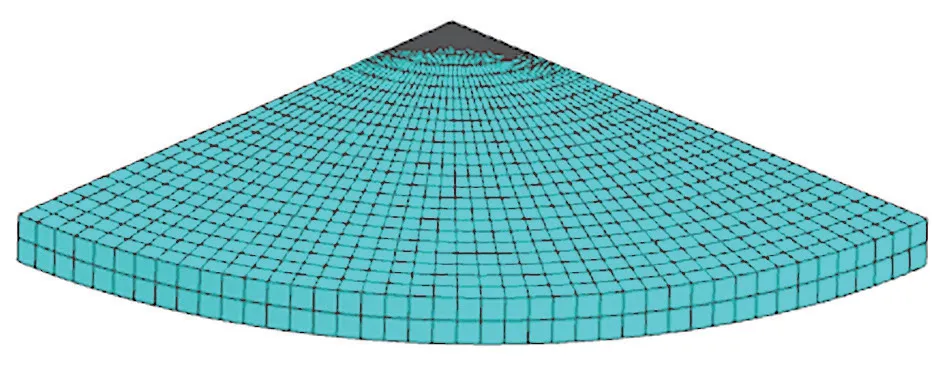
图1 毛坯的1/4 几何模型
为了研究各工艺参数对拉深成形性能的影响,必须了解拉深过程中毛坯各位置等效应力、等效应变。因此,选择图2 所示从拉深件边缘到中心的9 个位置进行观测。
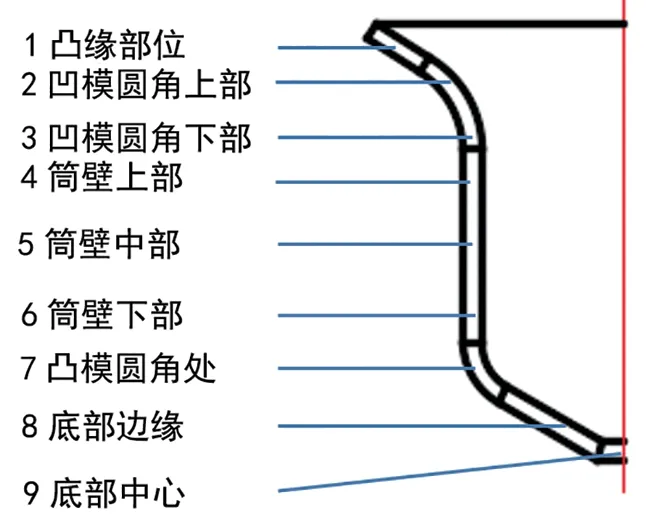
图2 测量位置
实验设计
Taguchi 法介绍
Taguchi 法主要用于研究设计实验,并确定工艺参数对成形零件性能的影响。通过Taguchi 法可以减少测试次数,节省人力、物力和财力。对于静态优化问题,有三种类型的信噪比,即望小特性、望大特性和望目特性。在本工作中,主要针对厚度变化进行分析,其变形应越均匀越好。因此,本工作属于望目特性问题。
确定因子和水平
拉深成形的工艺参数主要包括坯料形状与尺寸、摩擦系数、冲压速度、压边力和凹模圆角半径等。本工作仅对凸模圆角半径、凹模圆角半径和冲压速度进行分析,每个参数设置3 个级别。按照Taguchi 法,采用3 因素3 水平正交试验设计L9(33)进行模拟。各因素和水平设置见表3,正交试验表见表4。在本研究中,分析的指标主要是等效应力和等效应变的分布情况。
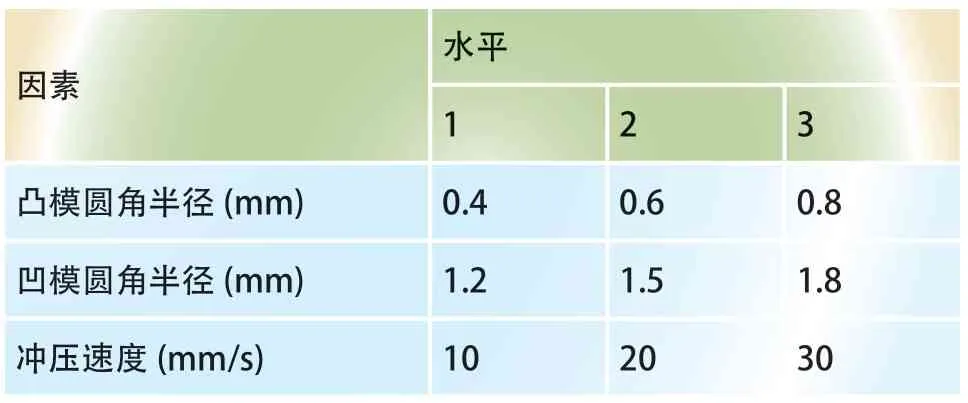
表3 工艺参数水平设置
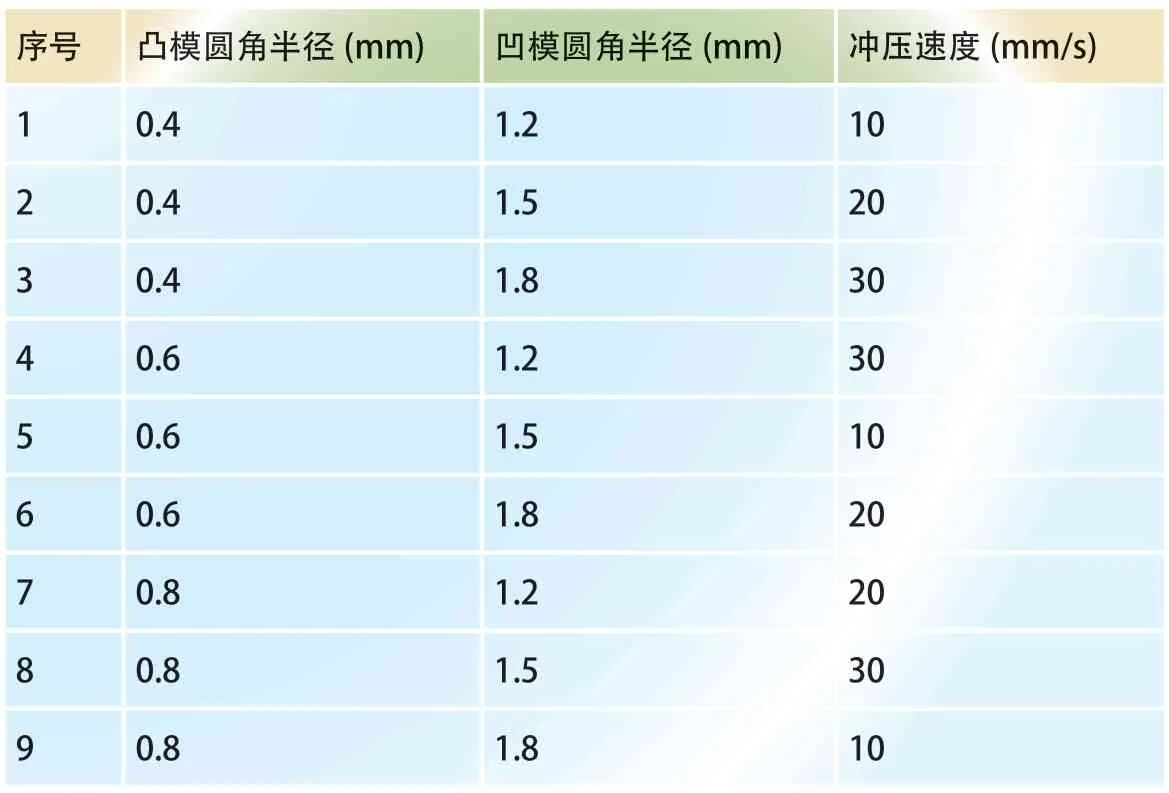
表4 正交试验表
结果与讨论
图3(a)和(b)所示分别为模拟编号1 的等效应力和等效应变分布情况。从图中可以看出,拉深件凸模圆角处、底部边缘的局部变薄非常显著,该区域极有可能由于应力集中而发生拉裂。模拟编号4、5 和9 也出现了显著的局部变薄现象。
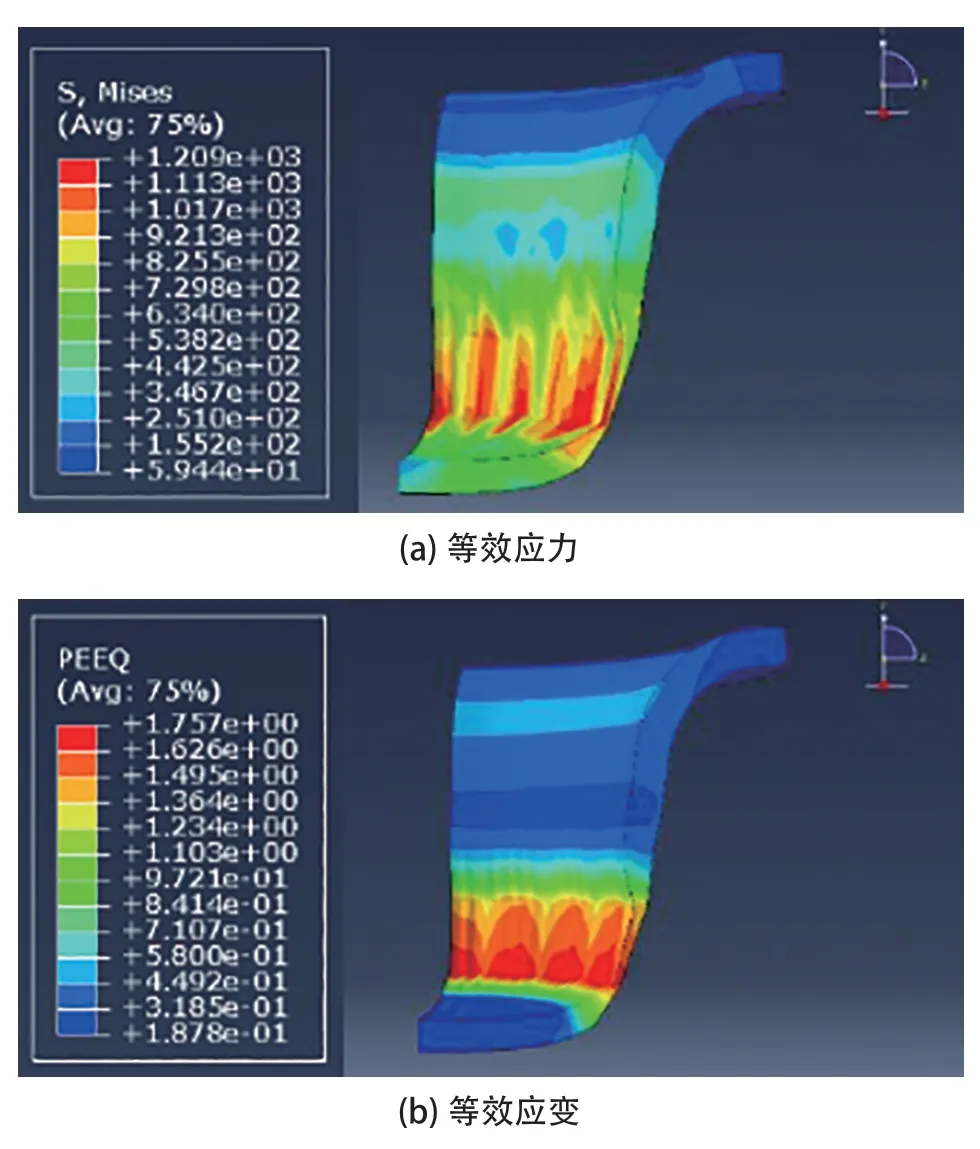
图3 模拟结果(模拟编号1)
在其他工艺参数不变的情况下,当冲压速度从10mm/s 增加到20mm/s、30mm/s 时,产品的可成形性更好。冲压速度为20mm/s,凸模圆角半径为0.8mm,凹模圆角半径为1.2mm 时的模拟结果如图4 所示(模拟编号7),此时产品的成形质量最好。结果表明,当凹模圆角半径保持不变,凸模圆角半径和冲压速度取不同的数值时,最大等效应力和等效应变的位置都会发生明显变化。
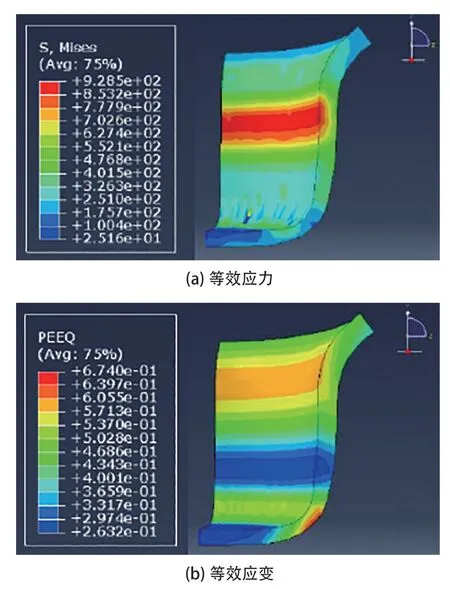
图4 模拟结果(模拟编号7)
当冲压速度为30mm/s、凸模圆角半径为0.8mm、凹模圆角半径为1.5mm 时,拉深模拟结果如图5 所示(模拟编号8)。此时,最大应变出现在凸缘部位;当冲压速度为20mm/s 时,最大应变出现在凸模圆角处。

图5 模拟结果(模拟编号8)
对于模拟编号2、3 和6,获得了与模拟编号8相似的结果。模拟编号7 获得了拉深产品的较大高度。结果表明,正确的工艺参数对获得所需的拉深产品质量和形状非常重要。
从凸缘部位到底部中心,拉深件9 个位置的等效应力分布如图6 所示,在某些模拟中,最大等效应力出现在两个或三个位置,且主要集中在凸缘部位和凸模圆角处。9 个位置的等效应变分布如图7 所示,最大等效应变分布在筒壁、凸模圆角处和底部区域。仿真结果表明,拉深产品的质量与凸模圆角半径、凹模圆角半径和冲压速度有直接的关系。
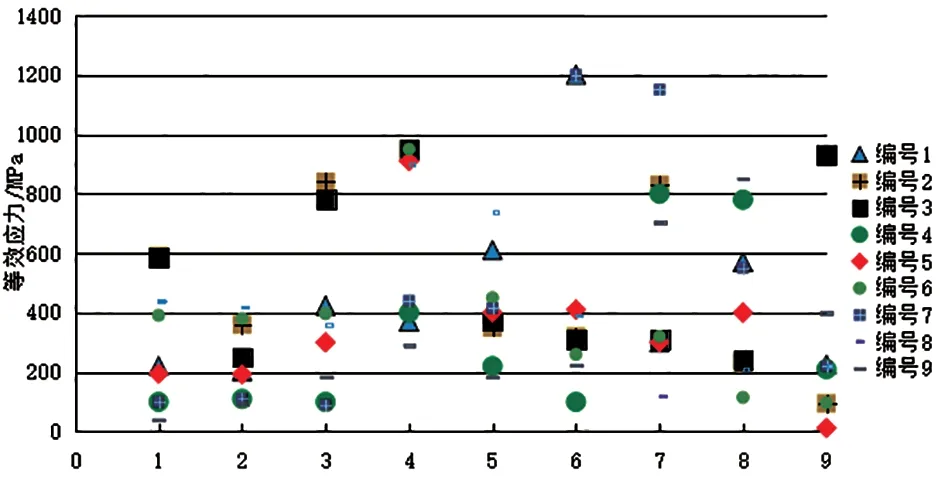
图6 凸缘部位到底部中心的等效应力分布情况
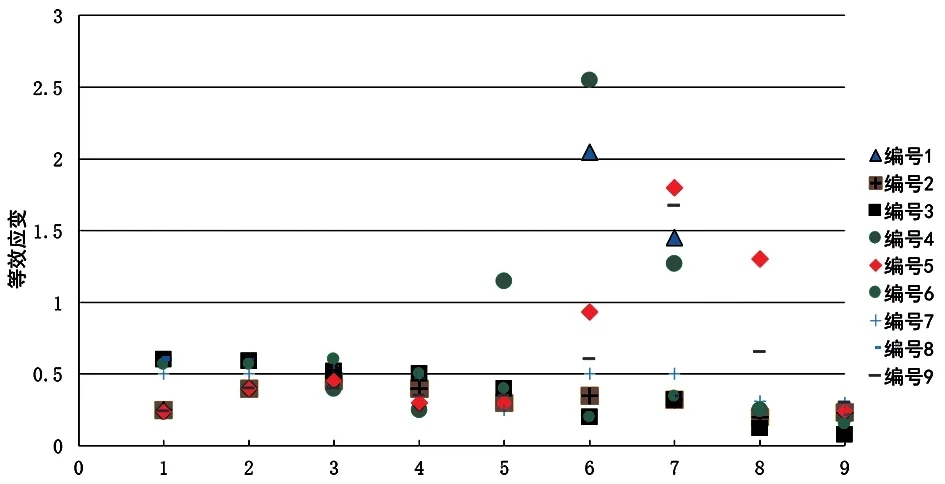
图7 凸缘部位到底部中心的等效应变分布情况
使用MINITAB软件和Taguchi法的信噪比特性(见表5 和表6),以分析各种因素对应力和应变分布的影响。表5 结果表明,凸模圆角半径对等效应力分布的影响最大,凹模圆角半径的影响次之,冲压速度的影响最小。表6 结果表明,对等效应变分布的影响从大到小依次为凹模圆角半径、凸模圆角半径、冲压速度。同时,冲压速度越快,生产时间越短,可成形性越好。
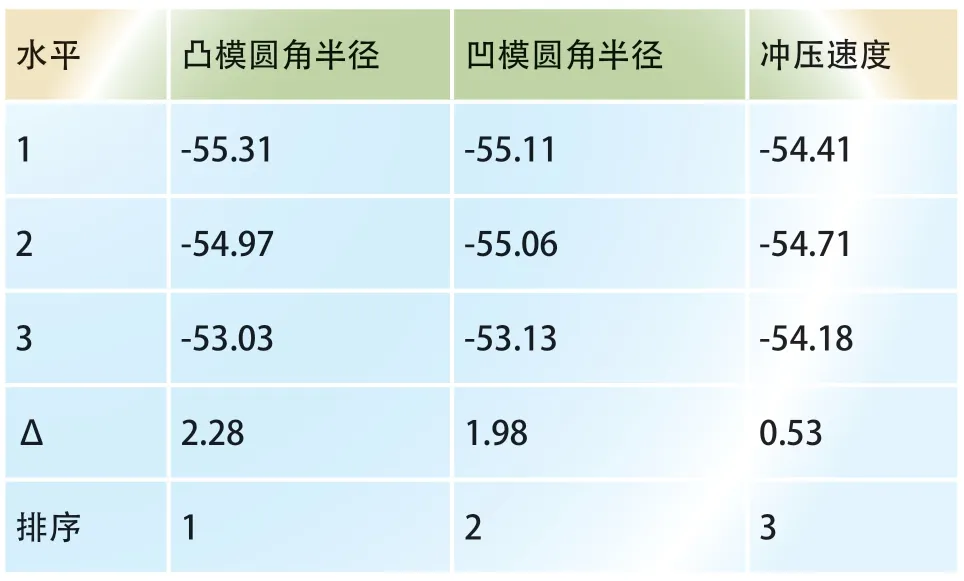
表5 等效应力分布的信噪比响应
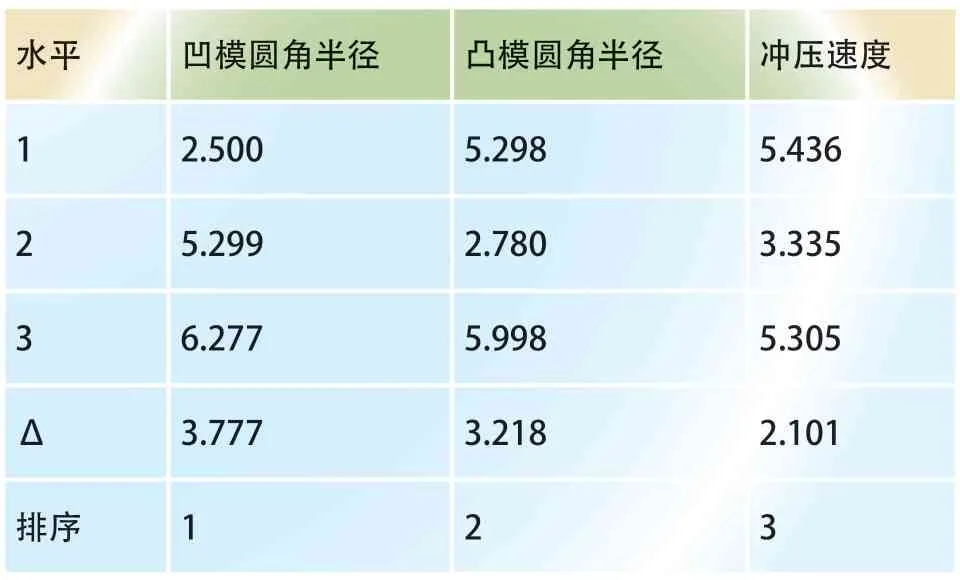
表6 等效应变分布的信噪比响应
结论
⑴凸模圆角半径对等效应力分布的影响最大,凹模圆角半径的影响次之,冲压速度的影响最小。对等效应变分布的影响从大到小依次为凹模圆角半径、凸模圆角半径、冲压速度。
⑵最大等效应力主要集中在凸缘部位和凸模圆角处。最大等效应变主要分布在凸模圆角处、筒壁和底部区域。
