基于二维Park 模型的风场尾流叠加方法

李乾，李华祥，朱敏，张日葵，周文韬

(1.南方科技大学嘉兴研究院，浙江 嘉兴 314000；2.深圳十沣科技有限公司，广东 深圳 518000)

0 引 言

无论是能源资源储量，还是生态环境承载力，我国已经达到或者接近上限，加速改善能源结构，提高清洁能源和可再生能源的使用比例已经迫在眉睫[1]。风能作为可再生清洁能源的一种，因其高效、可靠、可持续、可预测且具有成本竞争力的特性，而成为较有前途的化石能源替代能源之一。目前中国是世界风力发电的领头羊，风电装机容量已超过344 兆瓦[2]。

然而，随着风能领域的迅速发展，风机尺寸、机组规模也日益增大，风电机组尾流造成的严重后果日益凸显，特别是在大型风电场和风电基地中，如丹麦 Horns Rev 风电场内某些机组因尾流造成的年发电量损失高达90%以上[3]。因此，风力机尾流成为了风电领域的研究热点和前沿问题，受到了学术界和工程界的广泛关注。

尾流是指风经过风轮后产生的连续切向旋涡。大部分风电机组处于上游机组的尾流中，尾流区风速降低，湍流度增加[4]。解析尾流模型计算效率高，操作简易，从而被广泛应用，是风资源仿真应用中主要的尾流模型。然而，目前关于解析尾流的研究大多集中于尾流模型本身，重点关注单台风机的尾流影响，对于多台风机间尾流叠加效应的综合影响，风机群对风场的综合影响，相关研究则较为薄弱。因此，本文将结合前人多风机尾流叠加的经验，基于风机尾流对于风场的影响，构建适用于二维尾流模型的风场尾流叠加方法，以为其他研究者提供参考。

1 Park 尾流模型

1.1 风机尾流特性

在风力机运转过程中，其上下游流动可以大致划分为三个区域：上游诱导区、近场尾流区、远场尾流区[5]。基于风机上下游流动特征，Jensen 于1983 年提出Park 尾流模型[6]。Park 尾流模型是最初的解析尾流模型，其提出的顶帽分布（top-hat distribution）假设是解析尾流模型的基础。顶帽分布的示意图如下。

图1 顶帽分布示意图

由于实际风电场中机组之间一般相距7～8 倍风轮直径，且近场尾流的流动细节对远场尾流影响不大，因此解析尾流模型中会忽略压力恢复区的演化距离和膨胀，使用简化后的顶帽分布模型。

1.2 1D-Park 尾流模型

1D-Park 尾流模型[6]基于风轮轴向动量守恒推导，其风速亏损率表达式如下：

式中：Δu为亏损速度；U∞为来流速度；CT为风机的推力系数；kw为尾流膨胀（衰减）系数；x为风机下游点与风机在来流风向上的投影距离；rw为尾流半径；r0为风机半径。

1.3 2D-Park 尾流模型

Park 尾流模型主要考虑了风轮轴向上的动量守恒，属于1D 尾流模型。为满足真实流场中，径向尾流速度亏损率服从高斯分布的条件，2D-Park 尾流模型被提出，其表达式如下[1]。

式中：Δu为亏损速度；A为因风机下游点与风机在来流风向上投影距离造成的风速亏损；G为因风机下游点与来流风向方向上垂直距离产生的风速恢复；x为风机下游点与风机在来流风向上的投影距离；r为风机下游点与来流风向方向上的垂直距离；U∞为来流风速；rw为尾流半径；σ为高斯速度损失面的标准差。

2 尾流叠加方法

2.1 经典尾流叠加方法

在经典尾流叠加方法中，通常假定在风电场内，相邻风力机之间的间距大、尾流干扰弱，因此在计算孤立风力机尾流时，每个风力机轮毂处的平均风速都可以近似为自由来流速度。叠加时主要关注风机间的尾流叠加，仅考虑两种状态，风机群位于风场前以及风机群位于风场后。风场中的尾流效应的叠加，可以视作单台风机位于风场时产生尾流效应的叠加，具体叠加方式主要有5 种，包括几何叠加[7]、线性叠加[7]、能量平衡[8]、平方叠加[8]、取最小值[9]，5 种叠加方法的表达式如下：

a)几何叠加

b)线性叠加

c)能量平衡

d)平方叠加

e)取最小值

式中：vj为j号风机受到尾流前的风速；vwj为j号风机受到所有风机尾流后的风速；vi-wj为仅当i号风机存在时，j号风机受到尾流后的风速，该值由尾流模型计算。

目前，针对不同的风场，各经典尾流叠加方法的模拟结果往往各有优劣，有时可能均无法正确表征现场实测功率衰减变化规律[8]。在经典尾流叠加方法中，风场任意点位的尾流损失，通常可以由每个风机在该处的亏损进行线性叠加来获得，或者取亏损最大值。

2.2 风场尾流叠加方法

基于二维Park 模型的风场尾流叠加方法主要包含两个部分：风场尾流叠加方法和风机盘面尾流亏损模型。区别于关注风机间的尾流叠加的经典尾流叠加方法，风场尾流叠加方法考虑了风机群和风场耦合作用。该方法将风机群视作具有上下游关系的若干台风机，当上游风机置入风场时，其会与风场发生作用，风场的风资源条件会发生改变，下游风机相当于放置在考虑上游风机尾流影响后的新风场中。

风场尾流叠加方法的计算大致可分为以下四个步骤：

a)上下游关系确定

以来流风向α（测风塔处的风速方向或所有风机平均的风速方向）对风机进行排序，确定风机间的上下游关系。

式中： 为风机的坐标方向，s越小表示越上游。

b)风机尾流亏损计算

计算当前风场条件下，单台风机产生的尾流亏损。

式中：Δvw为风机尾流产生的速度亏损；F2D-Park为2D-Park 尾流模型的作用，该作用与风机输入的风速 以及目标点位置和风机位置 的坐标差有关。

c)尾流亏损叠加，将风速亏损Δvw与风场风速 进行叠加，计算上游风机影响后的新风场风速。

d)循环步骤b)至步骤c)，直至所有风机产生的尾流亏损叠加完成。

2.3 风机盘面尾流亏损模型

经典尾流叠加方法主要基于早期的一维尾流模型提出，通常使用下游风机轮毂高度处的风速亏损，代替整个盘面的风速亏损。虽然这种方式在计算上会比较简易，但是，最新大量研究表明风机的尾流亏损基本满足高斯分布，仅使用轮毂高度处的风速作为亏损的平均值进行计算可能存在误差。因此，本文综合考虑有无尾流时下游风机盘面上的风速分布特征，提出了风机盘面尾流亏损模型。该模型以风机盘面的平均风速亏损代替风机轮毂高度处的风速亏损。

在自然条件下，风速分布大多可以用风廓线模型[10]进行近似。因此，在受到尾流之前，风机盘面平均风速vM和轮毂高度处风速vH的比值η1如下：

式中：S为盘面的面积；h为盘面上任意一点的高度；hH为轮毂的高度；α为风切变；R为风机半径；ρ为极坐标的长度值；θ为极坐标的弧度值，π为圆周率。

参考麦克劳林公式[11]，保留3 阶无穷小，记

可得

由于α通常小于1，因此vM小于vH，以半径50m，轮毂高度80m 的风机为例，当风切变α为0.1时，vM≈ 0.9956vH。因此，对于自然来流的风速，可以直接用轮毂高度处的风速近似，或使用η1进行校正。

当上游风机产生尾流时，如果下游风机位于上游风机的尾流区域，下游风机会受到尾流影响，尾流交界面如下图所示。

记风机盘面尾流亏损比例为ηW。在经典叠加方法中，通常使用轮毂高度处的尾流亏损，或者该亏损与上游风机造成的尾流盘面与下游风机盘面的交界面面积与下游风机盘面面积比值的乘积作为风机盘面尾流亏损比例。记该经典叠加方法的尾流亏损比例为ηWH：

式中：ΩI为上游风机造成的尾流盘面与下游风机盘面的交界面；S1为上游风机尾流盘面的面积；S2为下游风机盘面的面积；A为因风机下游点与风机在来流风向上投影距离造成的风速亏损；G为因风机下游点与来流风向方向上垂直距离产生的风速恢复；x1-2为下游风机轮毂与上游风机轮毂在上游风机风速方向上的投影距离；sr为下游风机轮毂与上游风机轮毂在上游风机风速方向上的垂直距离。

本文提出了一种风机盘面尾流亏损模型，该模型以盘面上的平均尾流亏损比例ηWM作为风机盘面亏损。在2D-Park 尾流模型中，对于下游风机，其受到上游风机作用下的尾流亏损比例ηWM的计算公式如下：

式中：y为以O1为原点；O1O2为坐标轴的坐标值；z为以O1为原点，垂直O1O2为坐标轴的坐标值，如图2 所示；r1为上游风机尾流盘面的半径；r2为下游风机盘面的半径。

图2 尾流交界面

由于该积分的计算过程较为复杂，在此，本文提出了一种简化的计算方法，通过构建Heaviside 函数[12]，以离散化的方式计算尾流亏损比例ηWM，该计算公式如下。

式中： 为空间点与上游风机尾流盘面的符号距离（内正外负）； 为空间点与下游风机盘面的符号距离（内正外负）。以A=1、r1=50、r2=40为例，不同sr时，三种方法的计算结果如下。

如图3 所示，简化方法能够较为精确的求解ηWM，而经典方法计算的求解则与精确解存在较大的偏差，且计算结果会在sr较小时偏大而在sr较大时偏小。

图3 盘面亏损结果对比

图4 双风机尾流干扰

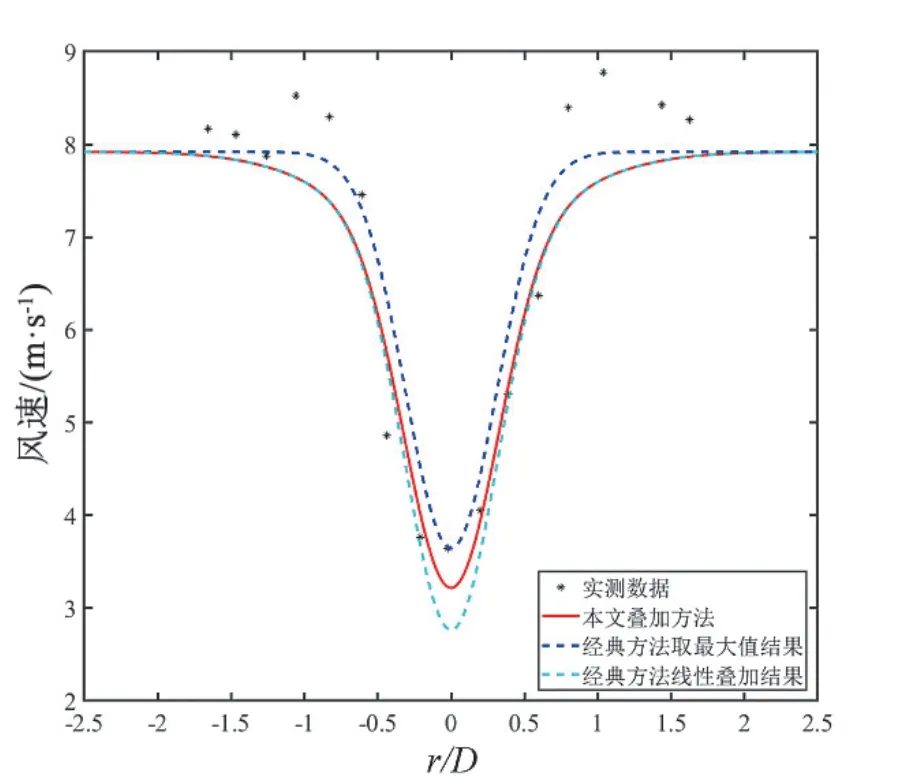
图5 A9-2 下游 2D 距离处的风速

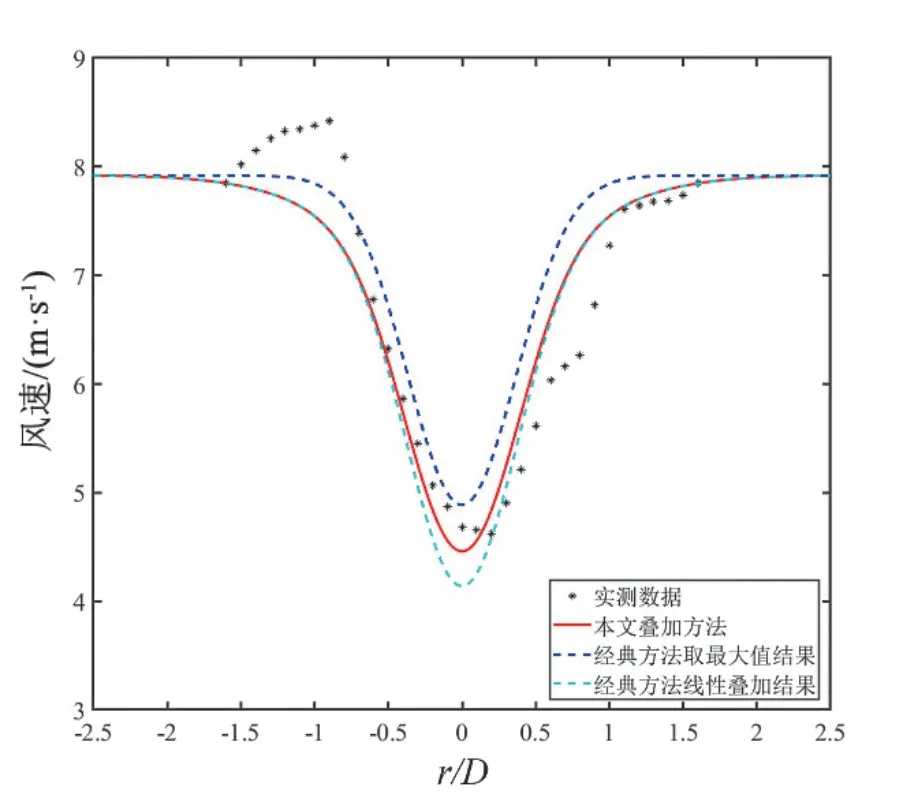
图6 A9-2 下游 3D 距离处的风速

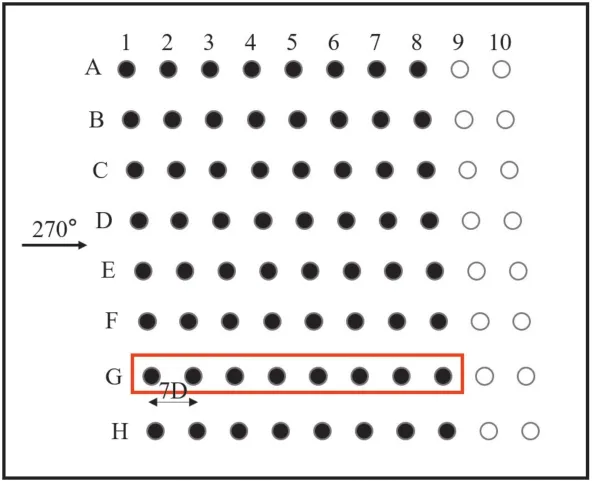
图7 Horns Rev 海上风电场布局

3 案例分析

3.1 石人风电场实验

石人风电场位于河北省，其中风力机 A1-4和A9-2 串联。刘智益等[13]采用多普勒激光测风雷达对该两台风机进行了相关的测风实验，该实验数据较为充分，能够直接反映尾流叠加效应的机理。本文以石人风电场实验数据[13]作为输入，该实验中含有两台风机A1-4 和A9-2，两风机的轮毂绝对高度均为1865.6m，风机直径D均为77m，湍流强度均为0.082311，风速均为7.92m/s，推力系数分别为0.777、0.892，风机间距离为6.419D，如下图所示。

该案例3 种尾流叠加方法的计算结果如下（Park 模型中需要考虑湍流修正，kw取0.195）。

各叠加方法与实测数据的偏差ε计算公式如下。

式中：vCAL为模型计算结果；vM为实测结果；i为实验数据的编号；m为实验数据总数。各叠加方法与实测数据的偏差ε计算结果如下表所示。（计算时已剔除大于来流风速的实测数据）

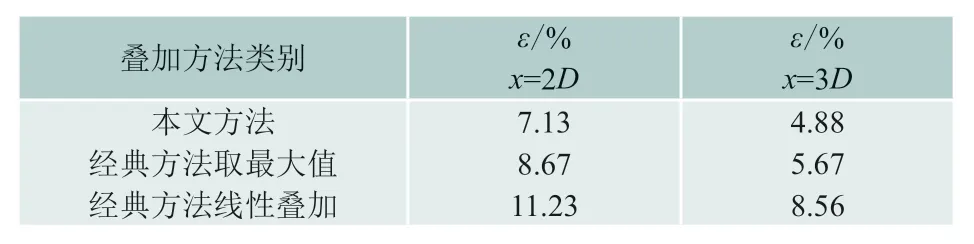
表1 偏差计算结果

由上述图表可知，由于考虑了尾流叠加影响，本文模型计算的尾流损失比经典模型取最大值方式计算的尾流损失要高。同时，由于考虑风机盘面与尾流盘面的关系影响，本文模型计算的尾流损失要比经典模型线性叠加方式计算的尾流损失要低。整体上，本文模型的尾流计算结果与实验测量的尾流结果更为吻合。

3.2 Horns Rev 海上风电场

Horns Rev 海上风电场位于丹麦东北海域，离岸距离约15 km，由 80 台维斯塔斯公司V-80-2MW 型风机组成，水平方向风机的间距为7D，风机的轮毂高度为70m，风机直径为80m。该风电场风机布局[14]如下。

在此本文主要分析了270°来流风向，来流风速为8m/s，推力系数为0.8 条件下，G 行前8 台风机尾流前后的功率比值ηi。

式中：i为风机的编号；PW为考虑尾流后的风机功率，P为考虑尾流前的风机功率，各方法功率预测结果与实测结果对比如下。（图中实测数据和LES 模拟结果均来自Shayan 等[15]的论文。）

如图8 所示，本文提出的风场尾流叠加方法结果更为准确，能够较为准确地反映多台风机并存时不同风机间的干扰作用。通过提出风机盘面尾流叠加方法，减少了下游风机在上游风机中心时，可能存在的尾流损失过度估计，进一步提高了预测精度。

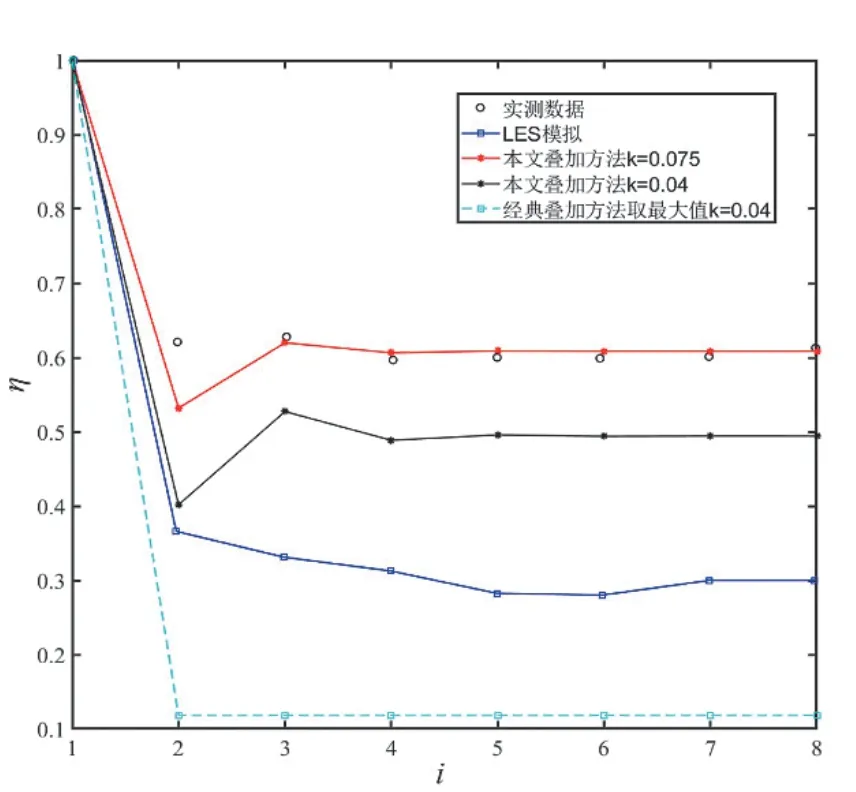
图8 功率预测比较

6 结论

为充分考虑风机群中多台风机间的干扰作用，构造出精确的尾流叠加方法，本文基于风机上下游关系，综合考虑风场与风机间的相互影响，提出了风场尾流叠加方法。基于二维尾流模型高斯分布的特征，提出了风机盘面尾流亏损模型以及相应的盘面风速亏损简化计算方法。在此基础上提出了基于二维Park 模型的风场尾流叠加方法。使用该方法对河北石人风电场和HornsRev丹麦海上风电场进行尾流预测，结果表明：

1)本文叠加方法可以较好地预测风场中的尾流损失，且预测结果相较于经典方法更为精确。

2)相较于直接使用风机轮毂高度的风速亏损，通过积分的方式计算风机盘面上的风速亏损更为精确。

3)考虑上游风机对下游风机尾流前输入风速的影响，可以更加精确地描述风机群间多台风机的干涉作用。