混合建模方法在蒸汽供热管网建模中的应用

胡佳怡，郑梦莲

(浙江大学 热工与动力系统研究所，浙江 杭州 310027)

0 引 言

随着我国能源转型进程的进行，能源利用转向追求更加高效、清洁和智能化的用能。区域供热系统是重要的能源消费者之一，目前大多数区域供热系统仍采用燃烧化石燃料供暖，化石燃料的过多燃烧会增加碳排放从而影响环境，因此，提高我国区域供热系统的能源利用效率十分重要，对供热系统的准确建模有利于准确估计系统的能源使用情况，从而进行运行分析和调度控制[1-2]。

对供热系统进行建模的方法包括水力计算、热力计算和水力热力耦合计算。水力计算通常采用图论法[3]，建立水力瞬态模型可以为管网的有效运行提供基础[4]。而阻力系数是水力建模过程中的一个重要参数，对其进行辨识有助于提高建模准确性[5]。热力计算则通过热力公式和模型对管道进行数值求解从而求得温度分布[6-7]。在实际供热管网中，水力和热力参数相互影响，因此还需要进行水力热力耦合建模[2,8]。

由于管道结构及材料老化等影响，采用上述机理方法仍可能存在建模误差。数据驱动方法是一种黑箱模型，根据历史数据进行建模，避免了复杂的机理建模，已被用于评估供热管网的热损失和热需求[9]。但是数据驱动方法由于物理模型缺失会导致可解释性弱和外推性差等问题，因此本文提出通过数据—物理混合建模来对供热管网进行建模。混合建模方法在建筑节能[10]、电池健康度预测[11]和电力系统[12]等方面都有应用，根据其融合方法的不同可以分为以下三种类型：串联模型将一种模型的结果作为另一种模型的输入[13]；并联模型将数据驱动模型和机理模型的结果通过加权等方式进行叠加得到最后结果[14]；引导模式以机理方法为主，通过数据驱动方法预测其中的某些未知参数或环节[15]。现有的文献更多地讨论了混合模型与数据驱动模型或物理模型之间的差异[16]，而对不同混合建模方法的比较较少。因此本文着重探讨不同混合模型的建模效果比较。

目前工业园区的蒸汽供热管网建模主要以机理建模为主，本文考虑了机理建模与数据驱动混合的建模方法进行建模，从而提高模型精度，并比较了三种混合建模方法的区别。

1 方法

1.1 水力热力模型

水力模型基于质量守恒定律和能量守恒定律，离散的管段模型不利于计算，图论方法可以将其抽象为矩阵从而方便水力计算。以下为图论计算方法，首先定义节点—管段关联矩阵A 和基环-管段关联矩阵B：

其中，m为管段数；n为节点数；k为基环数。

质量守恒定律可以表示为：

其中，G为流量向量，kg/s；g为净流量，无泄漏和疏水情况下为0，kg/s。

环能量方程可以表示为：

其中，ΔP 为各管段的压降，MPa。

蒸汽供热管道的压降计算公式如下：

其中，λ是沿程阻力系数；L为管段长度，m；d0为管道内径，m；ρ为工质密度，kg/m3；v为管内蒸汽流速，m/s；α为局部阻力与沿程阻力的比值。

管段摩擦阻力公式可以表示为：

其中，K为管壁绝对粗糙度，m。

管道的阻力系数定义如式（11）所示，已知阻力系数及流量则可以方便地计算管段压降。

其中，S为管段阻力系数。

热力模型通过计算内外温差及保温热阻来计算管段散热量，对于双层保温管道，其单位管长散热量可以表示为：

其中，q为单位管长的散热量，W/m；η为管道散热修正系数，与管道结构、保温老化和环境热阻等因素相关，tavg为管内流体平均温度，℃；ta为环境温度，℃；λ1为内保温层导热系数，W/(m·℃)；λ2为外保温层导热系数，W/(m·℃)；αo为环境散热系数，W/(m2·℃)；d1为管道外径，m；d2为内保温层外径，m；d3为外保温层外径，m。

通过下式可以计算蒸汽管道的沿途温降：

其中，h1为管道起点焓值，kJ/kg；h2为管道终点焓值，kJ/kg。

对于实际供热管道，水力参数与热力参数存在着相互影响的关系，单一的水力模型或热力模型可能导致结果不准确，因此，本研究经过热力水力参数迭代后得到最终的管网机理模型。

1.2 混合建模方法

本文主要采用串联式、并联式和引导式三种混合建模方法对管段的压力和温度进行预测，其建模流程如图1 所示。并联建模方法先采用机理方法进行水力热力计算，然后采用数据驱动方法对实际值与机理值之间的误差E 进行预测，最后将机理结果和误差E 叠加得到最后的预测结果。串联方法将机理方法得到的计算结果作为数据驱动方法的输入，再通过数据驱动方法对压力和温度进行预测。引导方法先通过数据驱动的方式，对水力热力模型中的阻力系数和散热修正系数进行辨识，再将辨识结果代入机理模型中进行计算。

图1 混合建模方法示意图

1.3 最小二乘辨识

最小二乘方法具有简单和运算速度快的特点，传统的非线性最小二乘求解方法高斯牛顿法容易出现雅可比矩阵的问题，而Levenberg-Marquard（LM）方法则可以避免相关问题的发生[17]，因此，本文采用LM 方法对阻力系数和散热修正系数进行辨识。

辨识阻力系数的目的是使得辨识后的压力观测值与预测值之间的误差最小，其目标函数可以表示为：

其中，pp是压力预测值，MPa；pr是压力观测值，MPa；是权重系数，这里取1；M是观测点数量；NLC是总数据量。

考虑到阻抗的实际值与计算值的偏差应该在一定范围内，设定阻抗的约束条件可以表示为：

其中，Si是第i条管线的阻抗值；ci和di是第i条管线的阻力系数上下界搜索系数。

同理，辨识散热修正系数时目标函数可以表示为：

其中，tp是温度预测值，℃；tr是温度观测值，℃。散热修正系数的约束条件可以表示为：

其中，ηi是第i条管线的阻抗值；s和t是管线的散热修正系数上下界。

1.4 多输出高斯过程回归

供热系统建模过程中需对热用户侧压力温度进行预测，各个热用户处的温度和压力可能存在潜在的相关性。高斯过程回归是一种基于高斯过程先验知识得到预测结果的方法，单输出高斯过程回归输出为一个值，多输出高斯过程回归输出为一组向量，其核函数可以捕获输出之间相关性，因此，与多输出高斯过程回归相比，单输出高斯过程回归在解决多输出问题时可以得到更好的结果[18]，本文采用多元高斯过程回归方法建模。

2 算例

2.1 数据集

本文选取某工业园区的一部分支状供热管网作为研究对象，采集了该管网2020 年12 月某三天的流量、压力和温度数据，共4175 个数据点作为数据集。管网简化图如图2 所示，包括14 个温度压力测点u1-u14。计算所采用的管道和保温参数如表1 所示，参考城镇供热管网设计规范选择局部与沿程阻力比值[19]。

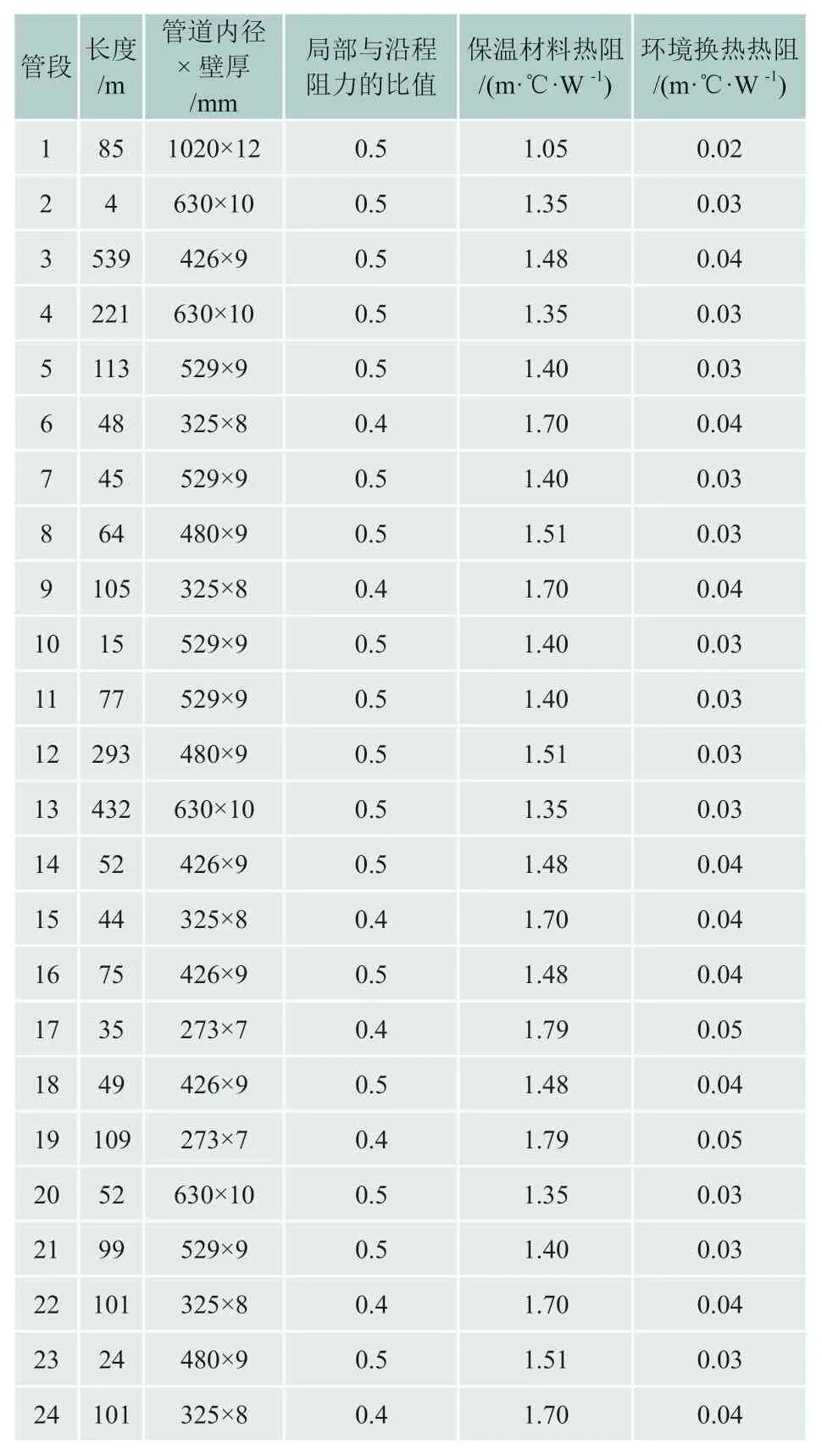
表1 管道设计参数

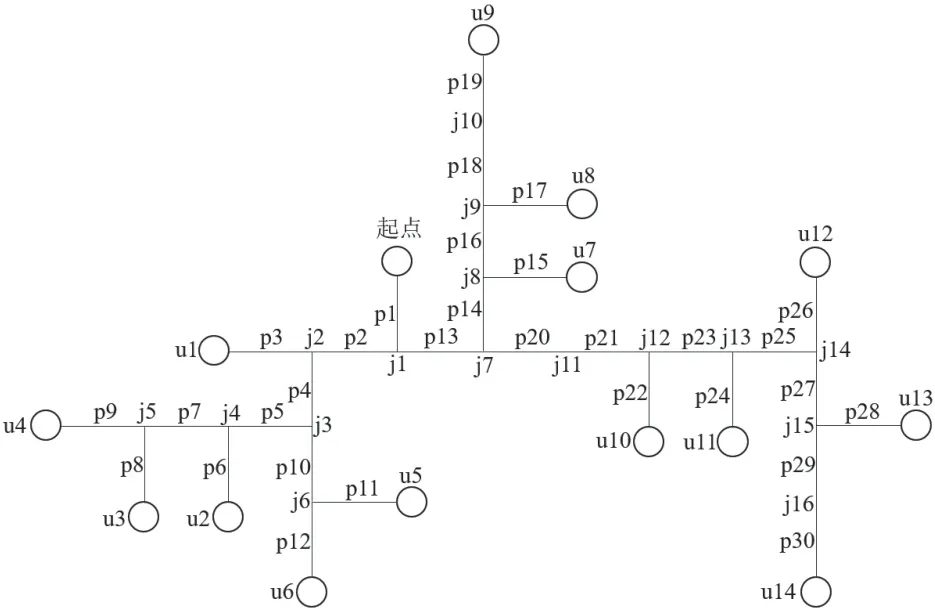
图2 支状供热管网示意图

2.2 水力热力模型参数辨识

计算阻力系数设计值时，考虑造成阻力系数辨识值与设计值偏差的原因是绝对当量粗糙度和局部沿程阻力比值的取值偏差，因此假设了绝对当量粗糙度和局部沿程阻力比值的上下限，作为辨识约束条件的系数ci和系数di，选取合适的上下限范围有助于辨识到更接近真实情况的阻力系数值，具体取值如表2 所示。

表2 管道当量粗糙度及沿程局部阻力比值

阻力系数的设计值和辨识值如表3 所示，部分阻力系数辨识值与设计值相差较大，可能是由于压力测点的仪表测量误差或未考虑到的局部阻力系数导致的。

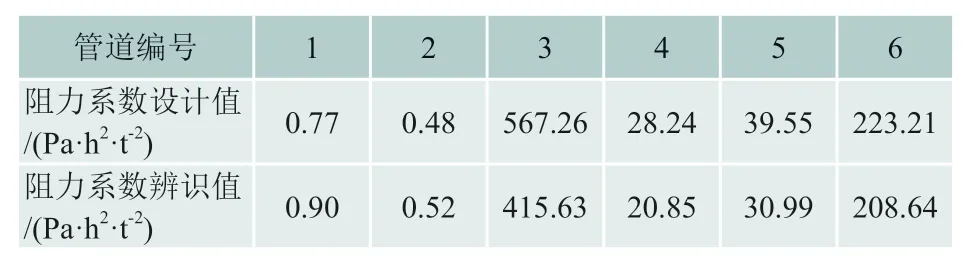
表3 阻力系数计算值

设置散热修正系数的上下边界s和t为1 和15。散热修正系数辨识值如表4 所示，部分管道散热修正系数偏大，原因是管道可能存在保温老化或局部破坏等问题，散热修正系数较小的管道保温情况相对良好。

表4 散热修正系数辨识值

2.3 混合建模结果

混合建模方法中，并联和串联建模方法采用多输出高斯过程回归对压力和温度进行预测，由于核函数的选取会影响建模精度，本文采用组合核函数来提高建模精度，选取的核函数由径向基核函数、Matern32 核函数和线性核函数组成。此外，数据集中训练集和测试集的比例为85%和15%，训练集用于模型训练，测试集用于最终的模型评估，模型评价指标包括均方根误差（Root Mean Square Error, RMSE）、平均绝对误差（Mean Absolute Error, MAE）和平均绝对百分比误差（Mean Absolute Percentage Error, MAPE）。图3和图4 分别是不同建模方法下温度和压力的预测结果，可以看到不同方法下预测结果与观测结果的变化趋势基本相同。几种建模方法中机理计算误差最大。图中大多数测点的温度机理计算值大于观测值，是因为机理计算低估了管道由于老化等原因造成的散热增加量，而大多数测点的压力机理计算值小于观测值，是由计算得到的阻力系数值偏大引起的。采用混合建模方法预测温度时，引导建模方法和其他两种方法预测值较为接近，采用混合建模方法预测压力时，引导建模方法结果与机理计算值更为接近，是因为引导方法以机理计算模型为计算基础，使得采用引导方法预测压力时更接近机理值，因此设定的机理模型的准确度会影响引导建模结果。

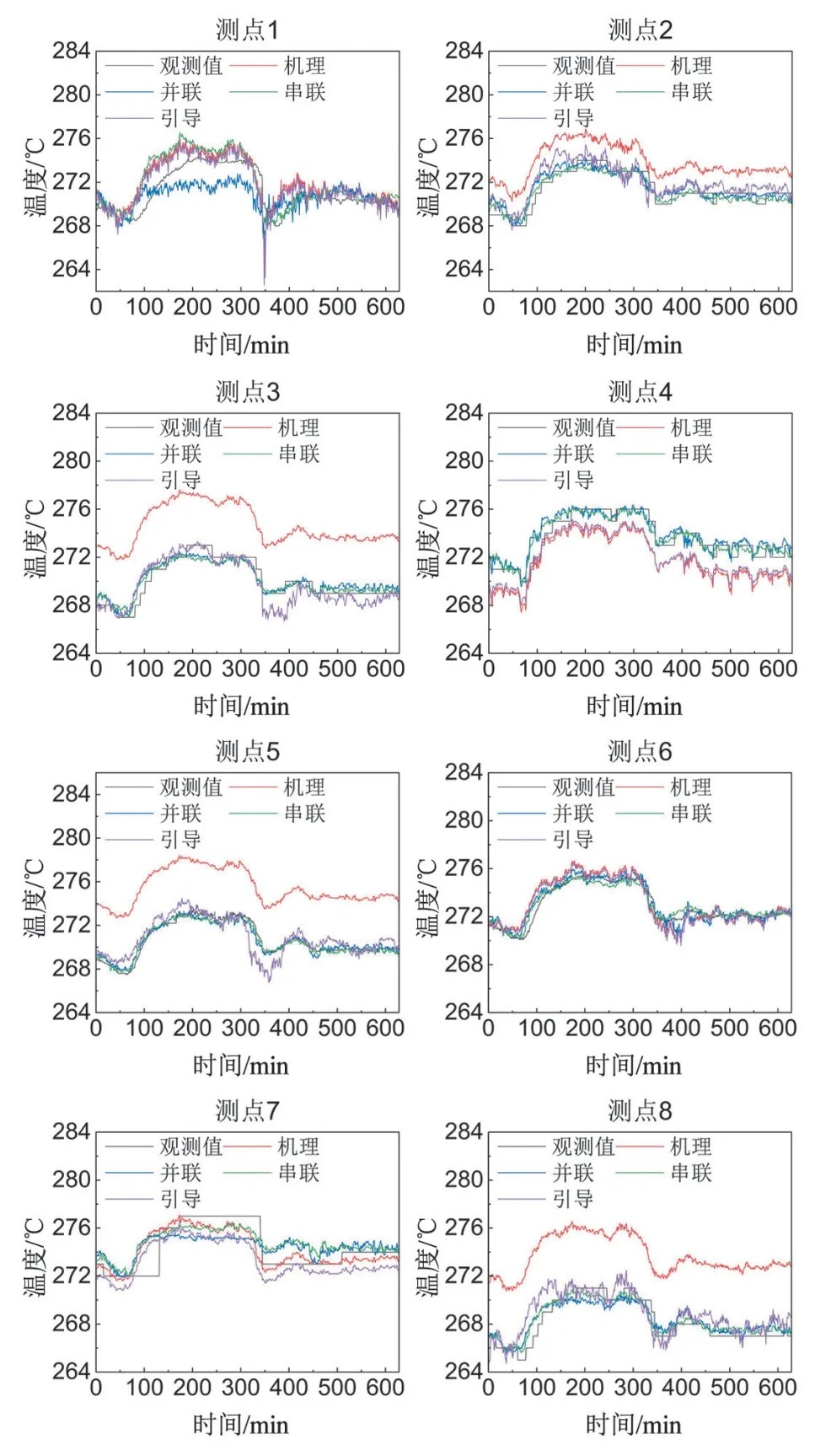
图3 不同建模方法下的温度预测结果比较

为了在统计意义上获得更准确的结果，采用随机划分的方法对测试集和训练集进行30 次不同的划分，温度和压力的预测结果误差如图5 和图6 所示。其中串联方法的预测误差较低，温度和压力测点的平均RMSE 分别为0.36 和0.0055，引导方法的预测误差相对较高，温度和压力测点的平均RMSE 为1.47 和0.043。由于串联模型结构的最后一层是数据驱动模型，本文数据集质量较好且机理建模结果可以较好地辅助数据驱动模型预测，因此得到了较好的预测结果。并联模型是机理结果与数据驱动结果的叠加，其精度取决于数据集是否能准确预测机理结果与实际值之间的误差。引导模型预测结果受到机理模型影响，因此机理模型误差导致了引导模型预测精度低，但是往往引导模型更能反映真实物理趋势且具有一定的外推性。

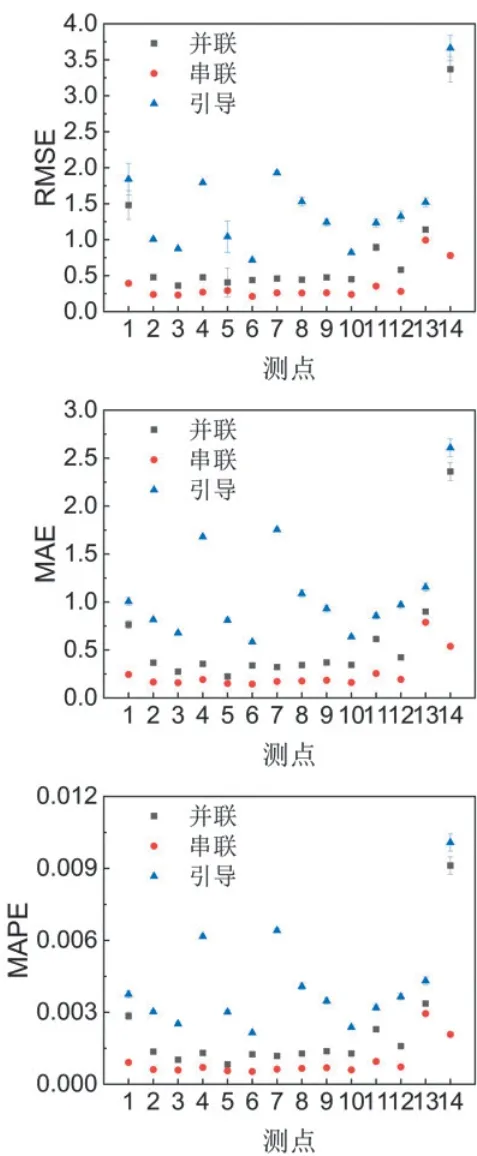
图5 混合建模方法的温度预测误差

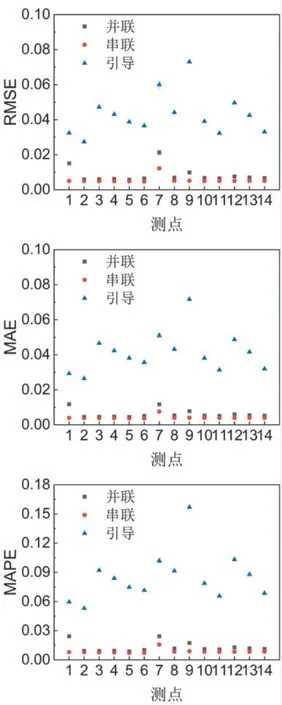
图6 混合建模方法的压力预测误差

3 结论

本文采用不同建模方法对工业园区的供热管网进行热力水力计算，由于机理—数据混合建模可以避免单一机理模型和数据驱动模型可能存在的问题，本文提出了三种不同的混合建模方法，比较了不同建模方法之间的模型结构差异和建模结果差异。结果显示提出的三种数据—机理混合建模方法相比单一的机理计算方法可以得到更好的计算结果。采用本文数据集进行建模时，串联和并联建模方法预测精度较高，引导建模方法预测精度较低，由于串联模型和并联模型更加依赖数据驱动模型，因此在数据集质量较高的情况下可以采用这两种建模方法，而并联模型相比串联模型需要考虑目前数据集中的特征是否可以较好地用于预测误差，对于引导建模则需要考虑机理模型的准确性。