基于调车系统的技术站编组去向方案优化

方 波，魏玉光

(北京交通大学 交通运输学院，北京 100044)

编组去向方案是技术站日常车流组织的基础,编组去向划分的质量直接影响技术站调车线使用方案和车流组织的效率。在车站衔接方向及重车流到站不断增加的情况下,车站划分的编组去向数越来越多,导致目前大多数编组站调车线运用紧张、列车编组难度大、车流违编情况突出等问题。因此,优化编组去向方案是改善技术站车流组织现状的重要途径。

在国外,编组去向问题(Blocking Problem)通常被视为求解列车编组计划的首要子问题,大量专家学者对其进行了深入研究。其中,文献[1]提出早期求解编组去向问题的混合整数非线性规划模型之一;文献[2-3]将该问题视为一个网络设计问题,并分别设计分支定价算法和基于拉格朗日松弛的启发式算法对其进行求解;文献[4]则从大规模多商品网络流的角度将编组去向问题表述为一个混合整数线性规划,并提出求解该模型的大规模领域搜索算法。上述模型更加关注货物的运输成本和车辆处理成本(类似于改编成本),且约束条件包含车站允许编开的最大编组去向数量。但有所区别的是,文献[1]还强调了编组去向的最大和最小车流量约束。其中,最小流量约束可以确保所得编组去向方案每天都具有稳定的车流用于编发列车,这在国内研究中较少被提及。

国内技术站列车组织形式以单组列车为主,列车编组计划问题的本质是一个编组去向设计问题。关于该问题的研究较为丰富,除少数文献外,绝大多数文献[5-12]均从宏观路网层对编组去向问题进行建模和求解。而由于国内外运营管理和车站能力使用现状的差异,国内既有研究[5-12]更加关注车辆的在站停留时间,在模型中主要体现为目标函数以列车(或编组去向)集结车小时、车流中转改编车小时等消耗最小。此外,国内研究通常不直接考虑车站允许编开的最大编组去向数量,而是代之以车流占用的调车线数量,并将其表述为一个关于编组去向车流的分段函数[12]。该分段函数通常假设每条调车线只能由一个编组去向的车流占用,但这不适用于调车线资源紧张的技术站。为此,文献[5]在模型中设定两个编组去向的车流可共用同一调车线。

文献[6]将文献[1-5,7-12]中的模型都归纳为单点模型,即将每个车站都视为一个点,且不考虑车流的站内改编路径。这类单点模型虽然一定程度上简化了原问题的复杂度,但由于忽视了车流选择不同站内改编路径的车小时差异以及对设备能力占用的区别,导致模型所得结果与工程实际存在一定出入,当车流量较大时,所得结果甚至不可行。为此,文献[6]提出了多点列车编组计划模型,首次将一个技术站的到发车场视为不同的点,以此考虑车流的不同站内改编径路消耗并明确每个编组去向的到发车场。但由于忽视了有调车流在站内的折角改编概率以及不同编组去向的车流可共用同一调车线等情况,该模型仍存在一定局限性。

针对既有研究的不足,本文将双向编组站的上下行系统分别视为不同的点,并根据编组去向的车流结构引入有调车流在列车终到站的折角改编概率,构建基于调车系统的编组去向方案优化模型,以使所得编组去向方案更加符合运输实际。

1 问题描述

为分析既有单点模型和多点模型的不足,以一个典型纵列代双向三级六场编组站a为例分析车流站内走行路径。技术站a的站场示意见图1,假设b站编开了到达a站的编组去向Bb,a,且该编组去向吸引的车流包括b站至a站及其以远的车流Nb,a、b站至c站及其以远的车流Nb,c、b站至d站及其以远的车流Nb,d以及b站至e站及其以远的车流Nb,e。

图1 技术站a的站场示意

单点模型下编组去向Bb,a中的有调车流在a站内的改编路径见表1。其中车流Nb,c和Nb,e的改编路径称为顺向改编路径,而Nb,d的改编路径则称为折角改编路径。尽管折角改编路径相较于顺向改编路径增加了车流的二次解体、集结、转场等作业,但单点模型却并未考虑这些额外作业消耗,这也导致单点模型的理论车小时消耗偏小。

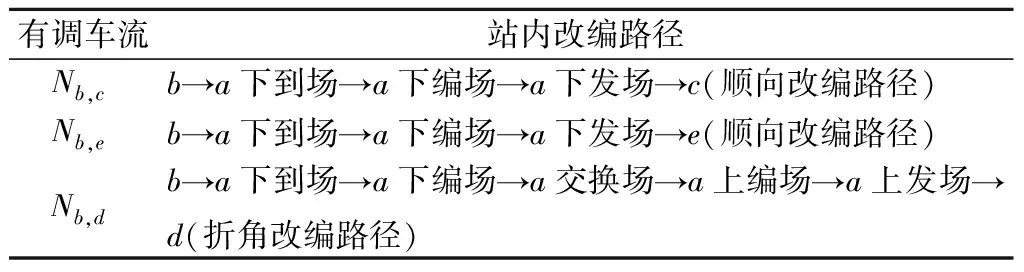
表1 单点模型下编组去向Bb,a中的有调车流在a站内的改编路径

而文献[6]中的多点模型则根据车流在双向编组站的接入和发出系统将车流划分为“下进下出”“下进上出”“上进上出”“上进下出”4种情形,不同情形下有调车流的站内改编路径见图2。根据a站的线路衔接情况,认为车流Nb,c(或Nb,e)和Nb,d可分别选择图2(a)和图2(b)中的任意一条站内改编路径,最终路径需经模型综合解算才能确定。

图2 不同有调车流的站内改编路径

尽管文献[6]的多点模型对既有单点模型的不足做了补充,但其设定每支车流最终只能选择一条站内改编路径使得该模型仍存在一定局限性。考虑以下情景:

(1)若b站编开到达a站的某解体列车中去往d站及其以远的货车数更多(如超过列车编成辆数的50%),而去往c站、e站及其以远的货车数较少,不考虑其余因素的影响,由于折角改编路径作业时间更长,列车从下行到达场经交换场、交换线路或其他场间联络线(或经枢纽环接)直接接入上行系统进行解体更加合理。此时,即使去往d站及其以远的车流属于折角车流,但也只需要经过一次解编作业,如图2(b)中的橙色改编路径所示;而列车中终到c站、e站及其以远的货车则先被解体至上行调车场,待去往c、e方向的交换车流集结至一定车数后,由调机将这些交换车流牵引至下行系统进行二次解编,如图2(a)中的蓝色改编路径所示。

(2)相反,若该列车中终到d站及其以远的货车数较少,而去往c站、e站及其以远的货车数占比更大,此时,列车直接在a站下行系统解体无疑更加合理,终到c站、e站及其以远的货车在a站只需经一次解编即可,如图2(a)中的橙色改编路径所示;而去往d站及其以远的货车则需经二次解编,如图2(b)中的蓝色改编路径所示。同理,还可给出文献[6]中“上进上出”和“上进下出”车流的可能站内改编路径(图2(c)和图2(d))。

上述例子表明,即便对于同一编组去向Bb,a,由于在编组去向始发站b编组的每列车的车流内容有所差异,该编组去向中的任意一支有调车流在a站的站内改编路径取决于其所在列车接入a站哪个系统进行解体。因此,同一车流在编组去向终到站均会有一定的概率被折角改编。

若b站只编开一个至a站的编组去向Bb,a导致a站的折角改编车数过多,则b站可同时编开至a站下行和上行系统的两个编组去向Bb,a(1)和Bb,a(2)。此时,将车流Nb,c和Nb,e编组到下行编组去向Bb,a(1)中,车流Nb,d编组到上行编组去向Bb,a(2)中,而终到车流Nb,a可编组到任意编组去向,则这两个编组去向中的任意有调车流在a站将不会被折角改编,有效减少了a站的折角改编车流量。但由于增开了一个至a站的编组去向,b站也将增加一个直达去向的集结车小时消耗。因此,b站是否同时编组至a站上下行系统的编组去向需经综合比选才得知。

综上,针对既有研究的不足,本文将双向编组站的上下行系统分别视为不同的点、单向编组站或区段站均视为一个点,提出基于调车系统的编组去向优化模型,以期实现:

(1)任意技术站按系统确定是否编开至另一技术站的直达去向列车。

(2)任意技术站是否同时编开至任意双向编组站上下行的两个直达去向列车。

2 模型构建

2.1 符号及说明

模型中的集合、参数及变量说明见表2～表4。

表2 模型中的集合及说明

表3 模型中参数及变量

表4 模型中变量及说明

(1)

其中,判断一支车流的OD是否属于集合Sj(1)和Sj(2)的条件是:

(1)任意终到双向编组站j的车流No,j(∀o∈V)可接入j站的任意系统,因此(o,j)∈Sj(1)且(o,j)∈Sj(2)。

(2)若No,d(d≠j)的车流径路包含j站,且根据j站衔接的方向,该车流最终可直接通过j站下行系统的出发场发出,则(o,d)∈Sj(1)。

(3)同理,若车流No,d(d≠j)的车流径路包含j站,且根据j站衔接的方向,该车流最终可直接通过j站上行系统的出发场发出,则(o,d)∈Sj(2)。

也即

(2)

(3)

2.2 模型假设

为便于求解,本文模型做如下假设:

(1)同一双向编组站的顺向改编路径的作业时间相等。

(2)同一双向编组站的折角改编路径的作业时间相等。

(3)若i站同时编组了至双向编组站j上下行系统的两个直达去向Bi,j(1)和Bi,j(2),则这两个去向的直达列车中不能含有折角车流。

(4)由于不同车站站内线路布局的差别及临时调度的灵活性,为简化模型,本文只考虑文献[13]中的第一种折角车流交换作业方式,即经交换场或交换线路递交折角改编车流。

2.3 目标函数

(1)直达去向集结消耗

技术站每编组一个直达去向就会产生一个集结车小时消耗。因此,所有编组去向每天的总集结车小时消耗Z1为

(4)

(2)有调车流的中转改编消耗

任意有调车流在单向系统技术站均只需经过一次改编。因此,有调车流在单向技术站的改编车小时消耗W1为

(5)

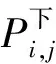
(6)

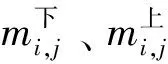
(7)

(8)

(9)

此时,有调车流在双向编组站的改编车小时消耗W2为

(10)

若i站同时编开至双向编组站j上下行系统的两个编组去向Bi,j(2)和Bi,j(1),则此时有调车流的改编车小时消耗W3为

(11)

因此,有调车流的总改编车小时消耗Z2为

Z2=W1+W2+W3

(12)

综上,模型的目标函数为

min(Z1+Z2)

(13)

2.4 约束条件

(1)编组去向数量约束。任意两技术站间可编开的编组去向数应满足

(14)

式(14)表示,若j站为单向系统技术站,则任意技术站i至多可编开一个到达j站的编组去向;若j站为双向编组站,则任意技术站i至多可编开到达j站上下行系统的两个编组去向。

(2)变量逻辑约束。只有当编组去向存在时车流才能编组到该编组去向中。分单、双向技术站考虑:

① 对于单向技术站j,应满足

(15)

式中:M为一个比较大的正数,可根据模型的变量规模取值。

② 而对于双向编组站j,任意i站编组至j站上下行系统的两个编组去向Bi,j(1)和Bi,j(2)总是成对出现;否则就代表i站至多只编组了一个到达j站的编组去向,即

∀i∈Vj∈VSY(o,d)∈S:No,d≠0

(16)

此外,若i站同时编组至j站上下行系统的两个编组去向Bi,j(1)和Bi,j(2),则这两个编组去向的车流量不能为0,即

(17)

(3)车流分配方案唯一性约束。对于i站可能编组至双向编组站j的编组去向,任意车流至多允许分配到其中一个编组去向中

(o,d)∈S

(18)

(4)改编能力约束。在技术站中转改编的有调车数不能超过车站的可用改编能力。由于有调中转车流在单向技术站只需进行一次改编作业,而在双向编组站可能需要折角改编。因此,分单、双向技术站分别考虑其各自的改编负荷为

① 对于单向技术站,需满足

(19)

② 而对于双向编组站,需分别考虑其上下行系统的改编车数。

a.下行系统:

(20)

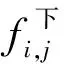
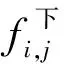
(21)

(22)

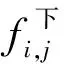
b.上行系统:

(23)

(24)

(25)

(5)调车线能力约束。各编组去向的车流占用的调车线数不能超过车站可用的调车线数量。分单、双向技术站考虑:

① 对于单向技术站,需满足

∀i∈VDY

(26)

(27)

② 而对于双向编组站,需分别考虑其上下行系统的调车线数量:

a.下行系统:

(28)

(29)

b.上行系统:

(30)

(6)流平衡约束。为保证将所有车流均能以唯一方案被运送到终点,需满足

(31)

(7)折角改编车流比例约束。研究指出,当编组站的折角改编车数占有调车数的比例超过15%时[14],会严重干扰车站正常作业。因此,为保障车站正常作业秩序,规定任意双向编组站的折角改编车流比例不能超过允许值βj,即

(32)

(8)最小编组去向约束。为保证所得编组去向方案的可执行性,一个编组去向吸引的车流量不应低于该去向的列车编成辆数,即

(33)

2.5 模型复杂度分析

设|V|=N,则有|S|=N(N-1),可估计文献[6]模型和本文模型的复杂度,见表5。

表5 不同模型的复杂度估计

由表5中的模型规模对比可知,本文模型和既有多点模型[6]的决策变量、约束条件阶数均为O(N3),两者复杂度相当,表明本文所建模型并没有进一步增加原问题的复杂度。

2.6 车流折角改编概率的近似计算方法

∀i∈Vj∈VSY

(34)

(35)

图3 有调车流的折角改编概率精确值与近似值对比

2.7 复杂约束线性化

注意到,上述模型的调车线约束式(26)、式(28)、式(30)为复杂的非线性约束。为便于求解,为中间变量φ1(x)引入4个0-1指示变量w1、w2、w3、w4分别表示x=0、0α是否成立,成立则取值为1,否则为0,则φ1(x)可线性化为

φ1(x)=0.5w2+w3+2w4

(36)

此时需添加约束

(37)

同理,为另一中间变量φ2(x)引入3个0-1指示变量u1、u2、u3分别表示x=0、0α是否成立,成立为1,否则为0,则φ2(x)可线性化为

φ2(x)=u2+2u3

(38)

同时添加约束

(39)

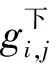
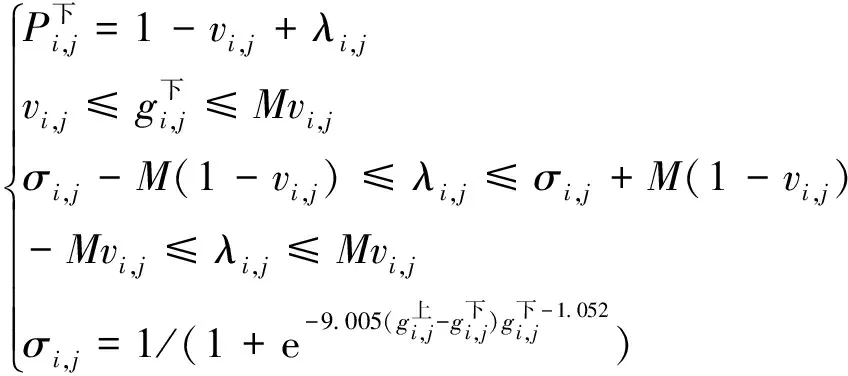
∀i∈Vj∈VSY

(40)

3 算例分析

3.1 小规模算例

为验证本文基于调车系统的非线性模型的可行性,利用同为多点模型的文献[6]中的小规模网络及数据进行模型验证,小规模路网示意图见图4。如图4所示,该路网共9个技术站,其中7个为双向编组站。

根据本文模型的特点,可直接调用GUROBI求解器得到精确解。但由于本文模型含有多个二次项且是非凸的,需将GUROBI的NonConvex参数设置为2,并将MIPGap设置为3%以避免长时间寻优。在最大折角改编车流比例为15%的条件下,求解得到该路网的车流总消耗为19 107车·h,9个站共有23个编组去向,编组去向方案见表6。其中,第5列的运行径路是直达去向列车在多点网络上的实际运行径路,包含了列车经过的双向编组站系统。本文模型虽未同文献[6]一样直接将车站的到发车场体现在决策变量中,但也可从编组去向的到发系统得到相同信息。此外,表6中部分编组去向的列车运行径路可能不止一条,如编组去向B9,2的列车运行径路可为9(1)→2(1)或9(2)→2(1)。因为根据技术站9的线路连接情况,去往技术站2的车流可直接从站9上行或下行系统出发场发出。

技术站能力负荷见表7。对于双向编组站而言,第3、第5列的“使用调车线数”=“各编组去向的车流正常占用的调车线数”+“交换车流混用的调车线数”。其中,被车流正常占用的调车线数可能不是整数,如技术站4为0.5条。这是根据本文模型的设定,车流量不足100车的编组去向可共用一条调车线,而由于技术站4只编组了一个到达技术站3的编组去向,且其车流量仅有73.4车(表6)。因此,模型认为该编组去向的车流占用0.5条调车线,而实际应视为1条。

表7 技术站的能力负荷(15%折角改编车流上限)

为与文献[6]的多点模型结果进行公平比较,不考虑本文模型的最小编组去向约束,在相同的参数设定下求解文献[6]算例在4种情形下的结果,见表8。

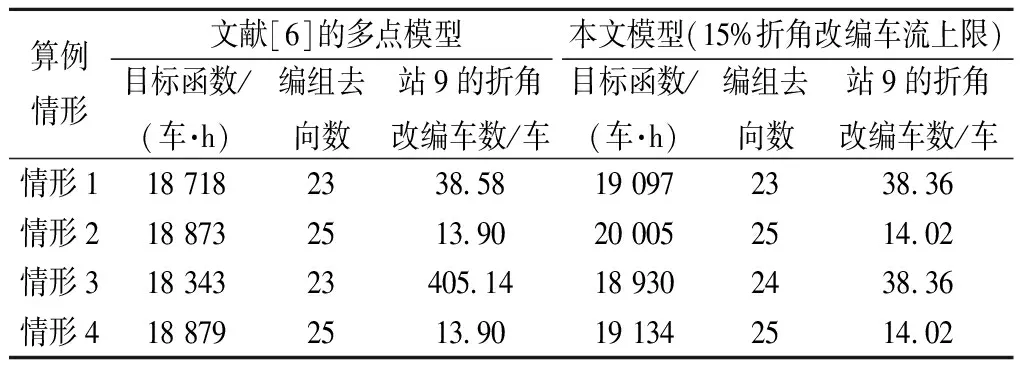
表8 不同模型的结果对比

由表8可知,在相同情形下,本文总车小时消耗虽比文献[6]的高255～1 132车·h,但由于本文考虑了车流的折角改编概率,结果更加符合实际。两个模型的总编组去向数基本相当,但本文模型在情形2(将站7上行系统的改编能力由2 200车缩减为100车)下,站9将同时编开至站7上下行系统的两个直达去向。此外,对比站9的折角改编车数可知,文献[6]模型在情形3下(此时文献[6]的多点模型等价于传统单点模型)的折角改编车数达到405.14车,占站9有调车数的38.5%,远高于文献[14]建议的15%。相反,本文模型下站9的折角改编车数最大仅有38.36车,对车站上下行系统的作业干扰较小。

3.2 中等规模算例

上述小规模算例验证了本文模型的可行性,为进一步测试本文模型在更大规模路网上的求解效果和其相较于传统单点模型的优势,以我国东部路网为背景,得到含32个技术站的中等规模单点网络及其多点网络示意,见图5。

3.2.1 与单点模型结果的对比

为了与文献[11]中的单点模型进行公平比较,不考虑本文模型的折角改编车流上限约束和最小编组去向约束,在相同参数和配置下(MIPGap设置为1%)分别利用两模型求解图5的中等规模路网,结果见表9。

表9 不同模型的结果

由表9可知,两模型在车流小于列车编成辆数的编组去向数和最小编组去向的车流量两方面基本相当,但本文模型的目标函数却比单点模型多7 042车·h。这是因为单点模型没有计算折角改编车流的额外作业车小时消耗。若按照本文模型的车流折角改编概率计算,则单点模型的目标函数应修正为253 541车·h,反而比本文模型结果多1 292车·h。

考虑车流的折角改编概率后,两模型下各双向编组站的折角改编车数见表10。其中,站7、12、14、16、20、22、24的折角改编车数均为0,故不予展示。

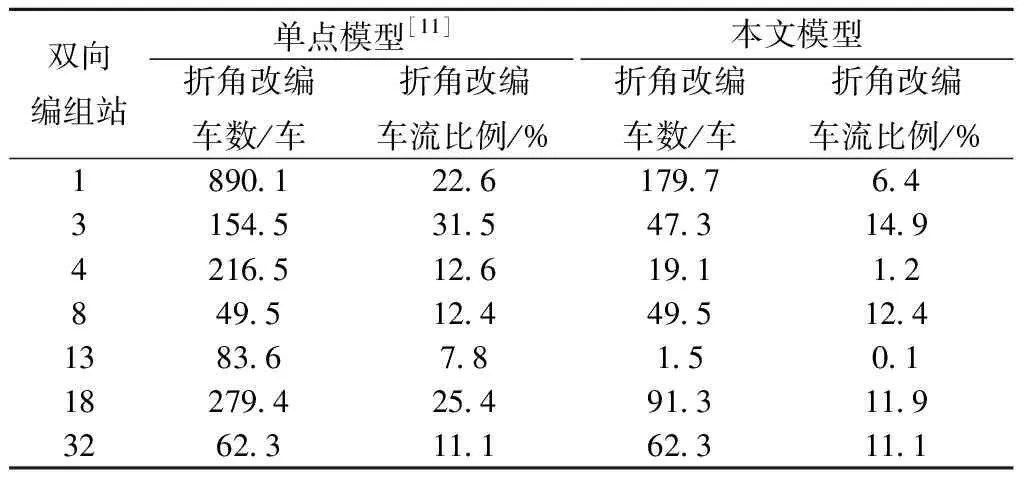
表10 不同模型下各双向编组站的折角改编车数及其占比

表10中的折角改编车流比例是指各双向编组站的总折角改编车数与有调车数的比值。在单点模型下,站1、3、18的折角改编车流比例高于15%,这将影响车站的作业效率。而在本文模型结果中,所有站的折角改编车流比例均低于15%,所得编组去向方案更符合实际要求。

3.2.2 折角改编车流上限约束对结果的影响

为考察无折角改编车流上限约束条件下各技术站的折角改编车数,松弛模型约束式(31)或将βj(∀j∈VSY)设置为100%。模型耗时1 060 s得到一个当前上、下界相对差距小于0.47%的可行解,目标函数为252 382车·h,共262个编组去向。其中,除7、12、14、16、20、22、24站外,其余各双向编组站的折角改编车数见图6。

图6 各双向编组站的折角改编车流及其占比(βj=100%)

图6中,松弛折角改编车流比例上限约束后,各技术站的折角改编车数占比不会超过15.7%,也即模型约束式(31)中的βj(∀j∈VSY)取值为15.7%～100%时对本文模型结果没有影响。因此,将βj从15%开始取值并以3%依次递减进行实验,结果见表11。

表11 不同折角改编车流上限约束下的算例结果

需要说明的是,当βj小于1.2%时,模型没有可行解。这是因为模型考虑了最小编组去向约束,部分车流必须合并到某些编组去向中并以一定的概率被折角改编。表11第二列是本文模型基于式(34)～式(35)的概率近似公式得到的目标函数值,7次实验平均耗时740 s。最后一列表示发站需同时编开至到站上下行系统编组去向的OD对集合。以βj等于15%为例,此时整个路网仅技术站14需同时编开去往双向编组站13上下行的两个直达去向列车。表11结果表明,随着车站允许的折角改编车流的减少,车流的总车小时消耗会增加,尽管总编组去向数变化不大,但由同一发站编开至同一到站上下行系统的编组去向越来越多。

如上所述,表9中的目标函数是基于Sigmoid函数的概率近似公式得到的近似值。为验证所得目标函数近似值与真实值之间的差距,利用式(6)～式(8)表示的精确概率对表9中的结果进行校正。两者的相对差距见图7,目标函数近似值比真实值增加不超过0.1%,表明本文拟合所得的概率近似公式合理且有效,模型的计算结果较为可靠。

图7 目标函数近似值与准确值对比

4 结论

优化编组去向是合理使用调车线、缓解编尾压力以及提高车站作业效率的重要途径。针对既有单点模型和多点模型的局限性,本文将双向编组站的上下行系统分别视为不同的点,并根据编组去向的车流构成引入有调车流的折角改编概率,提出了基于调车系统的编组去向方案优化非线性模型。随后对难以直接计算的车流折角改编概率进行了数值模拟,根据其变化规律,以Sigmoid函数为基础,拟合得到了车流折角改编概率的近似计算公式。算例结果表明:

(1)本文模型能够实现技术站按系统确定是否编开直达列车以及是否同时编开至任意双向编组站上下行的两个去向直达列车。

(2)与既有单点模型和多点模型相比,本文模型所得编组去向方案更加符合运输实际。

(3)本文拟合得到的Sigmoid函数是车流折角改编概率的有效近似,在不降低解的质量下,提高了模型求解效率。

折角改编车流是影响技术站货车中时和作业效率的重要因素。本文虽研究了折角改编车流对编组去向方案的影响,但只考虑了经交换场或交换线路递交折角改编车流这一种方式,实际折角车流的处理情况往往更加复杂、灵活。因此,完善折角改编车流的计算及处理方式仍是未来研究的重点。