黄土地区铁路近接路基变形分析及监测研究

赵文辉，韩 峰，王瑞琦，刘泽兴，王定顺

(兰州交通大学 土木工程学院，兰州 730070)

随着中国铁路网的进一步完善,新建铁路不可避免地要接轨既有铁路,形成近接路基段[1]。随着运营速度的提高,列车对上部轨道结构TQI参数变化更敏感和对轨下结构要求更高[2-3],如何保证近接路段列车的舒适性和安全性,控制轨下结构的变形是近接工程面临的技术难题[1]。

当黄土地区修筑近接路基工程时,对于既有路基结构在填筑阶段和服役阶段已发生一定的工后沉降,且强度降现象对沉降控制意义重大[4-7],结合工后沉降控制标准,明确其理论分析模型和工后沉降要求值是新建路基结构形式选取的基础和前提,近接路基工程断面见图1。黄土作为一种特殊土,土体结构在附加应力或水分增加的作用下容易产生显著的附加变形[8],且缺少黄土地区近接路基相关研究。在近接路段复合地基选择时,高压旋喷桩既满足施工机械净空要求低、工艺简单、施工周期短等特点,又可达到加固地基的目的。文献[9-10]分别结合不同临近工程研究了高压旋喷桩施工对既有结构的影响,发现高压旋喷桩施工过程中主要以侧向荷载的形式对既有结构产生影响。结合TB 10001—2016《铁路路基设计规范》[11]和文献[12-14],为保证新建-既有路基的协同作用,沿既有路基边坡位置进行台阶开挖,并于台阶位置布置土工格栅。

黄土地区铁路工程领域关于此类问题的研究较少,结构形式不明确。本文以黄土地区铁路近接路基实际工程为背景,结合静荷载和循环荷载下修正的Burgers模型,基于各阶段监测数据,分析既有路基填筑阶段和服役阶段沉降变化规律,研究新建旋喷桩复合地基施工和路基填筑对既有路基的影响,揭示近接路基结构新建-既有路基变形响应规律。

1 近接工程概况

1.1 工程地质条件

监测工点地层岩性主要为砂质黄土、粗砂、砾砂和下伏泥岩夹砂岩。结合地勘资料,各地层物理力学参数见表1,工程地质特征如下:

1.2 近接段路基工况及监测断面

近接段路基段位于兰州市永登县树坪镇,结合既有路基施工和运营资料,复合地基采用双动力水泥土搅拌桩进行处理,桩径50 cm,桩长13 m,桩间距1.3 m,设计时复合地基设计承载力要求不小于150 kPa,桩顶设置为0.5 m的开级配碎石垫层,垫层中间位置铺设一层双向土工格栅。基床表层、基床底层和基床以下路堤分别采用级配碎石(0.6 m)、掺4%水泥改良土(1.9 m)和渗水土分层填筑,开挖台阶位置布设不小于3 m的双向土工格栅。

新建路基地基采用高压旋喷桩复合地基,桩径50 cm,桩长13 m,桩间距1.4 m,桩平面采用正方形布置,复合地基承载力不小于155 kPa;坡脚外侧2 m设置应力释放孔,桩径0.5 m,纵向间距1.2 m,机械掏孔后孔内填碎石,孔口三七灰土封闭。基床表层、基床底层和浸水防护高程以下分别采用0.6 m级配碎石+0.1 m中粗砂+复合土工膜+0.1 m中粗砂、B组非冻胀渗水填料(0.8 m,渗透系数>5×10-5m/s)和渗水土(同基床底层)。

对于既有路基与新建路基分别采用沉降板(既有线路中心与路基坡脚位置)和沉降观测标监测(线路中心与路肩位置),同时新建路基施工前既有路基道砟坡脚位置纵向设置物位计,见图2。

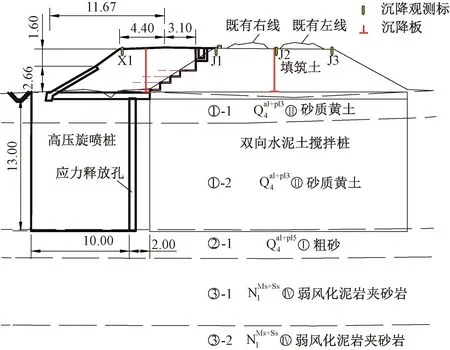
图2 典型断面图(单位:m)

2 理论分析模型

铁路路堤结构填筑完成后需不小于6个月的静置期,保证工后沉降要求,该阶段上部荷载仅为上部路堤结构自重。上部轨道结构铺设完成通车后,增加了上部轨道结构静荷载和上部列车动荷载。结合文献[15]可知,路堤结构层竖向动应力值随时间的变化接近正弦荷载,同时动应力衰减系数至基床底层底部位置已低于0.1,列车动荷载引起的路基累积沉降主要发生在基床部分[16]。

路基结构填料在各阶段受到的蠕变应力小于屈服应力,其流变可采用黏弹性流变分析,实测数据表明路基在静载或静动载复合作用下流变呈现出加速、等速和减速的变形规律,见图3。

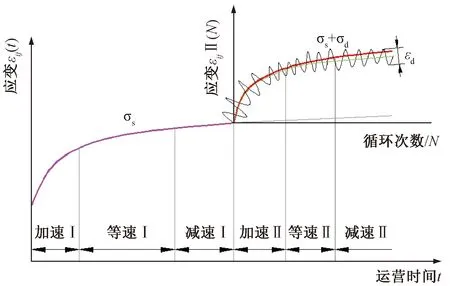
图3 荷载作用下路基填料层动态变形规律

Burgers模型具有应力-应变关系简单、参数概念明确、应用方便等优点,但精度不一定高。Burgers模型见图4。

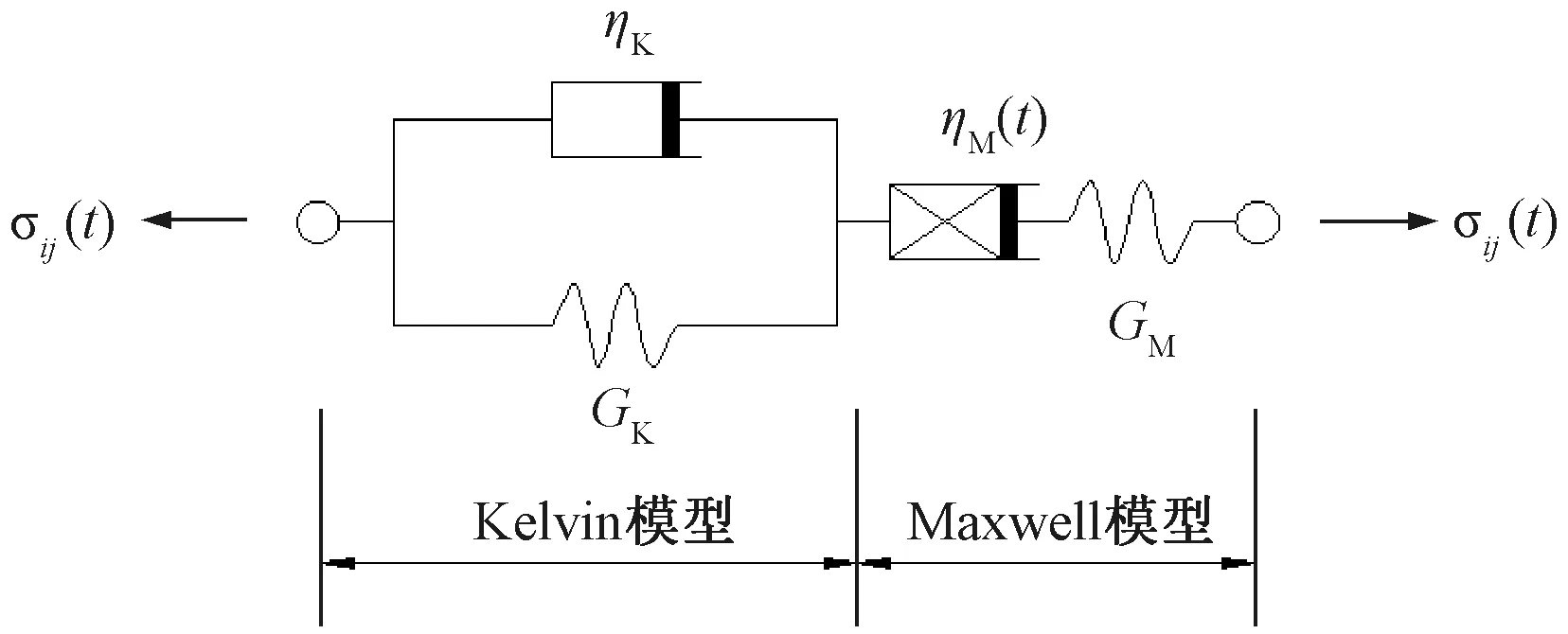
图4 Burgers模型

文献[17]采用其预测静载作用下路基长期沉降,Burgers模型适合描述应力大于屈服应力时的变形规律,变形为时间近似线性函数,但当应力小于屈服应力时,变形在初期阶段加速和等速发展后逐步趋于稳定[18]。基于Burgers模型,非线性修正Maxwell模型黏性元件,将粘壶单元扩展为广义粘壶,其黏度ηM(t)=AeBt,A、B为粘壶的黏度系数[19]。

2.1 静荷载下力学模型

由于路基结构层在服役过程中,累积沉降较小,在基于Burgers模型的土体蠕变方程进行求解时,假定应力作用下,土体体积变形受力瞬间完成,不随时间的延续而变化,同时泊松比保持不变。对于Maxwell模型,其本构方程为

(1)

式中:eij为偏应变;Sij为偏应力;GM为Maxwell模型剪切模量;ηM为Maxwell模型黏滞系数。

将竖向偏应力S11=2(σ1-σ3)/3代入式(1)并对t进行积分,并代入初始条件t=0,e11=(σ1-σ3)/(3GM)时,可得

(2)

对于Kelvin模型,其本构方程为

(3)

式中:GK为Kelvin模型剪切模量;ηk为Kelvin模型黏滞系数。

将竖向偏应力代入式(3)并对t进行积分,并代入初始条件t=0,e11=0时,可得

(4)

式中:K为体积模量。

结合式(2)和式(4),得到静力荷载作用下,其永久变形为

(5)

2.2 循环荷载下力学模型

在列车循环动荷载作用下,路基的永久变形由两部分构成:残余黏弹性变形和黏性流动变形。求解时,可将修正的Burgers模型分为Kelvin-Viogt模型和修正过的粘壶。对于Kelvin-Viogt模型,蠕变量J(t)为

(6)

第i个至第N个循环荷载作用,残余黏弹性变形εkvi为

(7)

将式(6)代入式(7),积分可得N次循环荷载作用下(t=NT),残余黏弹性变形εkvN为

(8)

式中:σd为附加动应力。

对于修正的粘壶,第i个循环荷载产生的永久变形εMi为

(9)

对式(9)积分,可得N个循环荷载作用,永久变形εMN为

(10)

综上所述,N个循环荷载作用下,路基的永久变形ε为

(11)

3 监测结果与分析

3.1 既有路基填筑阶段沉降观测结果分析

图5为既有线中心沉降板与沉降标沉降-填筑-时间关系曲线。由图5可知,对于既有线中心位置,2014年7月13日路基开始填筑,至2014年9月8日填筑至3.83 m,由于施工原因,路基本体填筑停滞3.27个月,而后填筑至设计标高4.26 m,经历6个月静置期,最后进行道砟及轨道结构铺设,至2015年7月15日铺轨完成,沉降量达77.541 mm,结合指数预测模型,预测总沉降量为79.060 mm,预测工后沉降量为1.519 mm;沉降标沉降值均随着时间的增长呈增大现象,且前期增长速率快,后期增长速率低,在2015年4月至6月道砟、轨道铺设阶段出现沉降快速增长,分析原因主要为冬雪融化、春季降雨及上部附加荷载造成路堤本体产生非常态永久变形[19];对于线路中心(J2)和路肩位置(J1、J3)沉降,J1和J3沉降相当,J2略大于J1和J3,路基横断面沉降呈现中心大、两侧小的规律。

图5 既有线中心沉降板与沉降标沉降-填筑-时间关系曲线

对于路基本体,当填筑完成后,路基结构承受填料和上部轨道结构自重产生的附加应力作用,结合TB 10621—2014《高速铁路设计规范》[20]可得上部轨道结构自重荷载和线间荷载可简化为矩形荷载p,其产生的附加应力σz可基于角点法计算,即

(12)

式中:m、n均为关于距离、竖向深度的参数。

叠加路基填料自重,可得到路基结构各层位的竖向应力。表2为路基变形预测模型参数,对于J2沉降表沉降-时间关系曲线,采用式(5)拟合可得到A=49 300 GPa,B=3.366×10-8s-1,相关系数为0.894,拟合度较高。

表2 路基变形预测模型参数

3.2 既有路基服役阶段沉降观测结果分析

结合研究资料[21-22],基床表层顶面动应力幅值σmax为

σmax=2.6P0×(1+αV)

(13)

式中:P0为机车车辆的静轴重,t;α为速度系数,本文取为0.003;V为车辆运行速度。

线路运行列车以CRH2、CRH5型动车组为主,平均静轴重为12.7 t,平均运行速度为160 km/h,计算可得基床表层顶面动应力幅值为48.9 kPa。路基动应力传递系数沿深度的变化规律见表3[5]。

表3 路基动应力传递系数

结合文献[15]可知,在考虑列车荷载作用下进行永久变形计算时,对于基床表层,计算可得T1为0.056 25 s,基床底层和基床以下路堤部分计算可得T2为0.562 5 s,对于作用次数N,基床表层N1为基床底层和基床以下路堤部分N2的4倍。结合既有线路列车运行图,得到各测试时间内动车组列车对数及编组数。图6为沉降标沉降-运营时间关系曲线,结合式(11),叠加不同测试时间内路基顶面以下3 m深度范围内沉降,拟合J2位置沉降可知,三位置沉降均随着运营时间的增加而增加,且前期增长速度较快,后期较慢;J2位置沉降较J1和J3位置较大,且运营约2.5年时,J2位置沉降基本稳定,稳定沉降值为1.257 mm;由于监测点冻土深度可达1.46 m,且J1和J3路肩位置监测点基础处于松弛区而非受力区,受自然应力影响较大,与J2位置相比,J1和J3位置沉降稳定时时间较长,且随着外界环境变化出现一定的波动现象;采用式(11)拟合J2位置沉降,黏度系数A=5.18×108GPa,黏度系数B=1.05×10-4s-1,相关系数为0.996,拟合度较高。

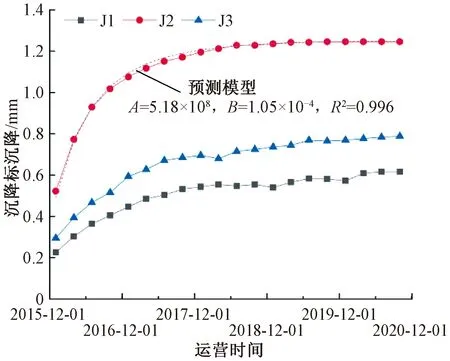
图6 沉降标沉降-运营时间关系曲线

3.3 近接路基施工阶段沉降观测结果分析

近接路基各阶段施工主要包括应力释放孔施工、高压旋喷桩复合地基施工、褥垫层施工和路堤本体分层填筑,其中,高压旋喷桩施工时,结合高压喷射注浆试验,注浆压力为25 MPa,提升速度约为0.2 m/min,施工顺序见图7,高压旋喷桩采用跳桩法相对既有线由近及远施工,即先顺序施工1→3→5排桩,等桩体强度不低于设计要求的50%后,施工2→4→6排桩。

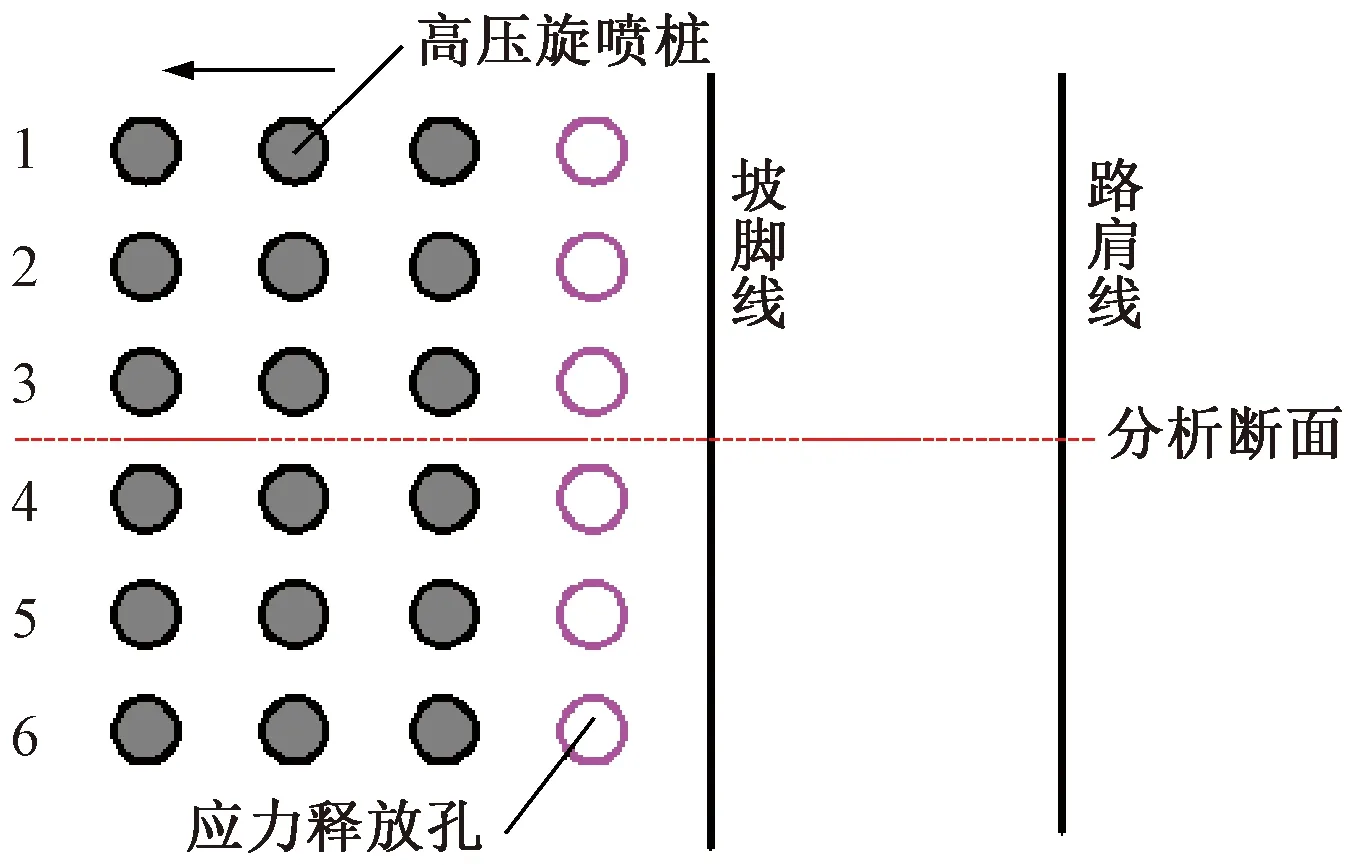
图7 高压旋喷桩复合地基施工顺序

基于高压旋喷桩施工工法对土体破坏的喷射动压和动量定律,结合文献[23-24]提出的喷射压力衰减经验公式为

(14)

式中:k、n为注浆工艺相关系数;m为拟合系数;d0为注浆设备喷嘴直径,m,本文取0.001 8 m;p0为出口压力值,kPa;x为喷嘴距中心轴位置长度,m。

经计算可得,桩周压力为220 kPa。图8为道砟坡脚隆起量随各排高压旋喷桩施工时间关系曲线,其中,单排桩施工时间为2020年10月8日,双排桩施工时间为2020年11月25日。由图8分析可知,分析断面道砟坡脚位置隆起量随各排高压旋喷桩施工均呈现先增加后波动性减小的现象,各排桩中临近既有线最近的旋喷桩施工对既有线影响最大,P1～P6排桩施工时,监测点附加最大隆起量分别为0.704、0.702、1.472、1.317、0.853、0.600 mm,说明近接段旋喷桩施工对既有线监测点的影响与距离成反比;对于各排桩施工时,当施工至距离顶面1/3～2/3位置时,对既有线影响最大;对于单排桩和双排桩,距离监测点相同距离时,单排桩施工对既有线造成隆起量相对较大,且施工完成后,单排桩施工完成后隆起量衰减速度较快,分析原因主要是双排桩施工时,单排桩已具有较高的强度,当施工时造成监测点隆起和施工完成隆起量下降时均起到限制作用;对于该分析断面,旋喷桩施工引起的最大隆起量为2.307 mm,满足既有线变形量控制值,说明设置应力释放孔和跳桩法施工,可减弱旋喷桩复合地基施工对既有线的影响。

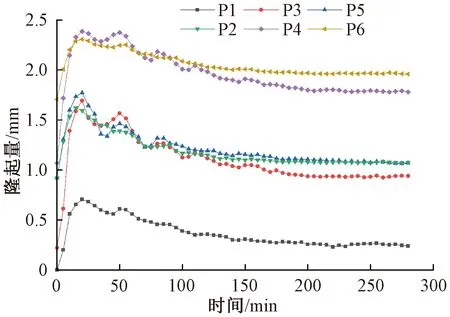
图8 道砟坡脚隆起量随各排高压旋喷桩施工时间关系曲线

近接路基路堤施工阶段主要分为垫层施工阶段和路堤本体填筑施工阶段。图9为既有与新建线路基沉降-填筑-时间关系曲线,分析可知,对于既有路基,垫层施工开始时,物位计沉降值为-1.531 mm,沉降标J1、J2和J3沉降值分别为-1.155、0.001、0.224 mm,对于物位计和沉降标变形是既有路基轨道结构自重、列车动荷载、旋喷桩复合地基等复合作用的结果,其中,对于物位计和沉降标J1位置,旋喷桩复合地基施工影响占主导作用,对于沉降标J2位置,旋喷桩复合地基施工和列车动荷载影响相当,对于沉降标J3位置,各因素影响均较小;结合不同填筑高度时附加沉降与距离帮宽侧路肩长度关系曲线见图10,随着垫层及路堤本体填筑高度的增加,物位计和沉降标J1、J2和J3附加沉降值均逐渐增加,且均随着填筑高度增加和距离帮宽侧路肩长度减小呈现非线性增加,主要原因是其随着新建路基填筑层填筑高度逐层增加。如图11所示,假定各层位为均布荷载,其对既有路基影响范围逐层增大,且对既有路基物位计和沉降标的影响幅值逐渐增加。

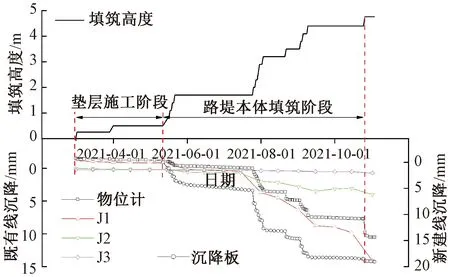
图9 既有与新建路基沉降-填筑-时间关系曲线

图10 不同填筑高度时附加沉降与距离帮宽侧路肩长度关系曲线

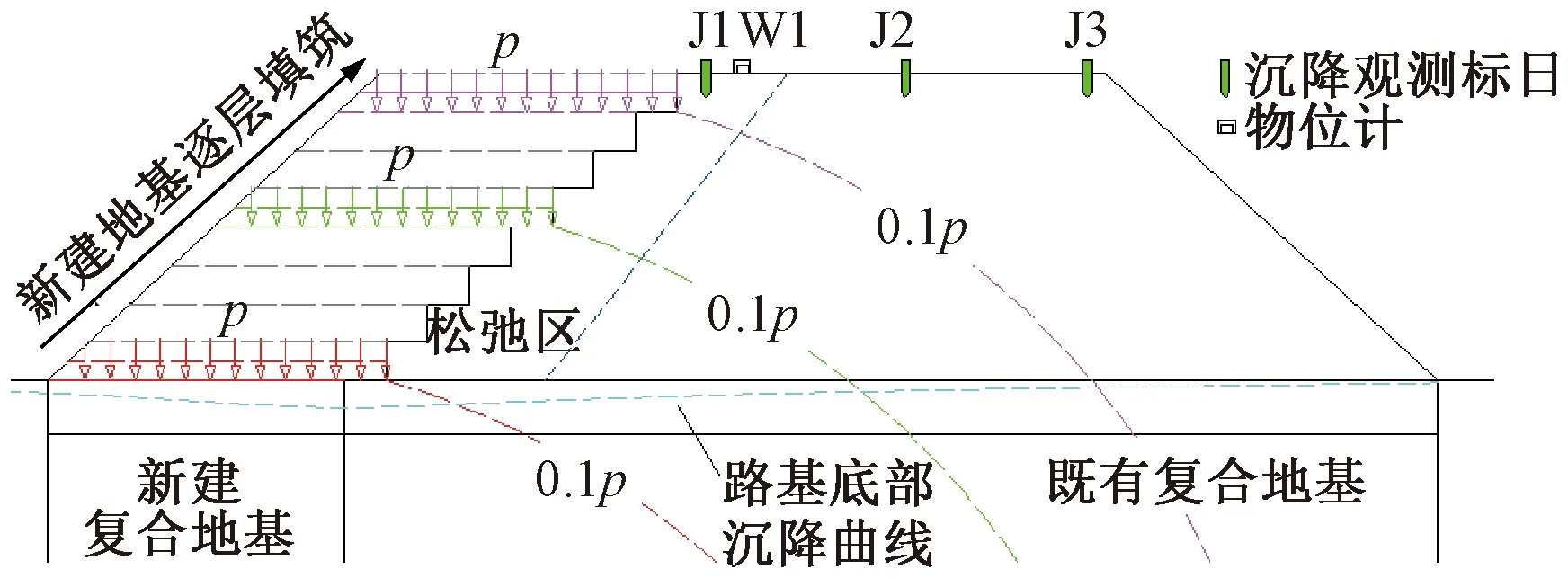
图11 各层位均布荷载对既有路基附加应力等值线示意

至2021年11月1日,沉降标J1、J2和J3附加沉降值分别为15.248、4.019、0.516 mm,沉降值分别为14.093、4.020、0.730 mm,均满足工后沉降值要求(≤5 cm)。在新建路基逐层填筑过程中,物位计位置附加黏性变形亦逐渐增加;新建路基沉降板沉降随着填筑高度的增加而增加,结合文献[25-28],由于作用至监测位置新建路基荷载、下部新建线与既有线复合地基刚度差异性及上部荷载作用下既有线复合地基对新建线复合地基起到侧向限制作用,综合作用下在监测点位置附近出现最大的沉降变形,同时为避免新建-既有路基差异沉降,在新建路基填筑时严格控制其压实度,至2021年11月3日沉降变形为19.041 mm。新建路基本体沉降尚未开展监测,但后期可结合静动荷载力学模型下修正的Burgers模型,确定各阶段新建路基工后沉降值和稳定时间,为近接段施工和运行提供技术支撑。

综合分析可知,结合各阶段观测结果及机理分析,对于该工点黄土地区近接既有路基工后沉降(≤5 cm)要求,既有路基填筑和服役阶段沉降由于结构自重、列车荷载和自然营力的复合作用呈现受力区大,松弛区小的规律。新建线复合地基施工和路堤施工引起既有线变形明显大于既有路基填筑和服役阶段沉降,但随着填筑高度增加和距离帮宽侧路肩长度减小呈现非线性增加现象,对于该工点各监测点各阶段沉降值均满足工后沉降要求。

4 结论

以黄土地区铁路近接路基实际工程为背景,结合静荷载和循环荷载下力学模型,基于各阶段监测数据,分析既有路基填筑阶段和服役阶段沉降变化规律,研究近接路基施工阶段新建-既有路基变形响应规律,得到以下主要结论:

(1)既有线填筑阶段,沉降标沉降值均随着时间的增长呈增大现象,且前期增长速率快,后期增长速率低,伴随局部的非常态永久变形;沉降沿路基横断面呈中心大、两侧小的现象;对于中心位置,沉降可采用非线性修正Maxwell模型黏性元件的Burgers模型拟合,相关系数为0.894,拟合度较高。

(2)既有线运营阶段,沉降标沉降均随着运营时间的增加而增加,且前期增长速度较快,后期较慢;中心位置沉降较大,且运营约2.5年时,沉降基本稳定。叠加不同测试时间内路基面以下3 m深度范围内沉降,采用循环荷载下力学模型拟合中心位置沉降,相关系数为0.996,拟合度较高。

(3)分析断面道砟坡脚位置隆起量随各排高压旋喷桩施工均呈现先增加后波动性减小的现象,旋喷桩施工引起的最大隆起量为2.307 mm,满足既有线变形量控制值;对于各排桩施工时,当施工至距离顶面1/3～2/3位置时,对既有线影响最大;距离监测点相同距离时,单排桩施工对既有线造成隆起量相对较大,且施工完成后,单排桩施工完成后隆起量衰减速度较快。

(4)随着垫层及路堤本体填筑高度的增加,物位计和沉降标J1、J2和J3附加沉降值均随着填筑高度增加和距离帮宽侧路肩长度减小呈现非线性增加,附加沉降值分别为15.248、12.049、4.019、0.516 mm,均满足工后沉降值不大于5 cm的要求。