基于EMD-DCC-GARCH的沪深300股指期货多尺度动态套期保值研究

王 佳, 何柳杨, 王 旭

(1.东北大学秦皇岛分校 经济学院,河北 秦皇岛 066004; 2.东北大学 工商管理学院,辽宁 沈阳 110819; 3.河北环境工程学院 经济与管理系,河北 秦皇岛 066102)

0 引言

期货市场作为金融市场的重要组成部分,主要通过套期保值策略实现风险转移功能。套期保值理论的核心问题就是确定最优套期保值比率。传统的完全套期保值策略要求套期保值比率为1∶1,即期货合约与持有的现货数量相等,方向相反。但由于基差风险的存在,期货价格和现货价格走势并不完全相同,套期保值比率为1的策略可能并不是最优。

随着套期保值理论的发展,现有估计最优套期保值比率的方法主要分为最小方差法、最小VaR和最小CVaR法。目前,已有许多学者利用最小方差法即套期保值投资组合方差的最小值,寻求最优套期保值策略[1]。BILLIO等[2]提出贝叶斯多链马尔科夫转换GARCH模型研究动态最小方差套期保值。王佳等[3]在传统DCC-GARCH模型的基础上,提出基于Markov时变转移的DCC-GARCH模型研究最小方差套期保值比率。近年来,最小VaR和最小CVaR套期保值理论逐渐发展,在金融领域得到了广泛的关注。PENG等[4]指出VaR在提高能源市场中的风险管理评估水平和套期保值绩效方面具有重要的作用。CHAI和ZHOU[5]研究基于半参数方法的最小CVaR套期保值策略,结果表明,在套期保值绩效方面半参数-最小CVaR法优于传统的最小方差法。余星等[6]分别构建方差、VaR和CVaR风险测度下的期货套期保值模型,并提出模型驱动下的最优套保策略决策准则。孙晓琳等[7]利用缓冲超越概率模型,构建CVaR约束下的最小化“厚尾事件”概率的套期保值策略,研究表明,该模型能够提供比最小化方差稳定的套期保值比率。

金融市场中有大量的投资者,异质性的存在使不同的投资者具有不同的套期保值期限。近来,有学者研究表明,最优套期保值比率的确定还依赖于套期保值期限,不同期限会存在不同的最优套期保值策略[8]。已有学者利用小波分析研究多时间尺度套期保值的绩效问题[9]。小波分析需要预先选定小波基,且在整个分析过程中将无法更换,因此小波分析的基函数缺乏自适应性。经验模态分解法(Empirical Mode Decomposition,简称EMD)作为小波分析的一种替代方法,受到了广泛的关注,它是一种自适应分解方法,可以对数据固有的震荡模式进行识别,实现原始数据的分解、简化和不同时间尺度的重建。目前,EMD方法已广泛应用于故障诊断[10]和信号处理[11]等领域,在金融领域的应用也逐渐增多[12]。WANG等[13]利用集合经验模态分解法(EEMD)将共同基金收益时间序列分为短期、中期和长期趋势,并分别研究不同时间尺度下共同基金的绩效。ZHU等[14]提出基于CVaR的经验模态分解方法研究碳市场和电力市场间的风险溢出效应。陆长玮[15]利用集合经验模态分解和周期相位识别方法研究上海房地产市场的多尺度周期波动问题。将EMD方法引入套期保值问题,评估不同时间尺度上的套期保值绩效,对于投资者优化资产配置进行风险管理,具有重要的理论和现实价值。

在现有研究的基础上,本文进行了如下改进:第一,已有关于多尺度的套期保值研究大多基于小波分析法。小波基的选择对于结果影响很大,缺乏自适应性,且处于局部最优的小波基,可能并不是全局最优。EMD是一种具有自适应性的时-频域分析方法,不需要预先设定基函数和分解层数,而是根据金融资产自身的复杂波动特征进行分解,能够更全面地揭示资产的内在运行机理。本文采用EMD方法将沪深300指数期货和现货收益率数据重构为短期、中期和长期三个时间尺度,并从方差贡献率角度讨论不同时间尺度的特点和重要性;第二,朱鹏飞等[16]将集合经验模态分解法(EEMD)引入套期保值比率估计过程,并利用考虑条件偏度和峰度的GARCH模型对我国沪深300指数现货和期货的套期保值问题进行研究。本文在其研究基础上,将EMD方法与具有时变特征的多元DCC-GARCH模型相结合,并分别研究最小方差和最小CVaR框架下的动态套期保值问题,估计最优套期保值比率,并将动态DCC-GARCH模型的套期保值绩效与传统静态模型的绩效进行对比使研究结果更加充分和完善。

1 模型和方法

1.1 经验模态分解法

经验模态分解法(EMD)是一种具有自适应性的时-频域分析方法。该方法可以将原始信号分解为若干个内涵模态分量(IMF)和残差项之和。IMF是指原始信号经EMD分解之后得到的各层信号分量。根据EMD的分解原理,任何复杂的数据信号xt(t=1,2,…,T)都可以依据以下步骤进行分解:

(1)根据原始信号上下极值点,使用三次样条插值分别画出上包络线xup,t和下包络线xlow,t;

(2)根据上下包络线逐点计算均值,画出均值包络线mt=(xup,t+xlow,t)/2;

(3)用原始信号减去均值包络线得到中间信号ct=xt-mt;

(4)判断ct是否满足IMF的两个条件。如果满足,则ct即为一个IMF分量,然后用残差项ηt=xt-ct代替原始信号xt;如果不是,则用ct代替xt;

(5)重复(1)-(4)步骤,直到满足停止规则。

IMF分量的获取通常需要若干次的迭代,当ηt变为一个单调函数时,无法从中提取更多的IMF。根据以上步骤,原始数据xt可以拆分为若干个内涵模态分量和残差项之和,即

(1)

其中,n为IMF的个数,ηt为残差项,cj ,t(j=1,2,…,n)为第j个IMF。

1.2 套期保值模型

1.2.1 最小方差和最小CVaR套期保值比率

假设套期保值比率为h,现货和期货在t时刻的收益率分别为Rs和Rf,投资组合的收益率Rp可以表示为Rp=Rs-hRf。最小方差条件下的最优套期保值比率h的表达式为:

h=ρσs/σf

(2)

其中,ρ为现货和期货之间的相关系数,σs和σf分别现货和期货收益的标准差。

风险价值VaR表示投资组合在一段时间内,在置信度水平α下所遭受的最大可能损失,表达式为:

Prob[r<-VaRp(α)]=1-α

(3)

其中,r表示投资组合在给定时间段的收益率。但VaR不具有次可加性,不满足一致性风险度量准则。CVaR克服了VaR的缺陷,其表达式为:

(4)

结合CVaR的定义和套期保值原理,在投资组合收益率Rp服从正态分布的假设下,经过一系列的推导,可得投资组合的CVaR计算公式[17]:

(5)

(6)

其中,Kα的数值会受到置信水平的影响,在90%,95%和99%的置信水平下,Kα分别为-1.7550,-2.0627和-2.6652。随着置信水平的提高,Kα逐渐减小。

1.2.2 静态套期保值模型

普通最小二乘法(OLS)是较为简单的套期保值模型,表达式为lnSt=α+βlnFt+εt,其中,回归系数β为最优套期保值比率h。在实际应用中,OLS模型中残差的自相关性可能导致伪回归问题,向量自回归模型(VAR)考虑了滞后项的影响,可以提高模型的准确性。VAR模型中每个变量都可以看成是其他变量滞后若干阶的形式,解决了一般模型对内生变量解释能力不足的缺点,其表达式为:

(7)

其中,lnSt-i为滞后i期的现货对数收益率,lnFt-i为滞后i期的期货对数收益率,i=1, …,k,εs,t,εf,t为残差项。其最优套期保值比率为:

(8)

1.2.3 动态DCC-GARCH模型

采用DCC-GARCH模型估计沪深300现货和期货间的动态套期保值比率。该模型的具体形式为:

(9)

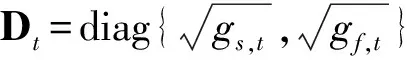
将DCC-GARCH模型估计得到的时变相关系数矩阵Rt代替式(2)和(6)中的ρ,分别得到最小方差法和最小CVaR法下的动态套期保值比率。

1.3 套期保值有效性指标

第一个指标为VaR。根据式(3),套期保值组合的VaR值表示在给定置信水平α下所遭受的最大可能损失。该指标值越小,表明在给定置信水平α下,套期保值组合达到的最大可能损失越小,该套期保值策略越有效。

第二个指标是风险降低比例(He),表达式为

(10)

He值越接近于1表示与无套期保值时现货的风险相比,套期保值组合的风险降低的越多,该套期保值策略越有效。

2 实证分析

2.1 数据

本文以沪深300指数期货和现货为研究对象。现货价格为沪深300每日收盘价。同一期货合约在不同交割月具有不同的期货价格,临近交割月的期货合约交易较活跃,应选取离交割月较近的期货合约收盘价作为期货价格,同时为避免到期日效应,选用沪深300股指期货下月连续的日收盘价作为期货价格。样本数据区间为2010年12月31日至2021年1月21日。所有的数据均来自于Wind数据库。

2.2 多尺度分析

利用经验模态分解法(EMD)对沪深300指数现货和期货收益率按照不同的时间尺度分解为9个内涵模态分量(IMF)和1个残差项。IMF周期依次由短到长,频率由高到低,残差项代表分解后数据的总趋势。将IMF分为短期、中期和长期三个时间尺度。IMF1到IMF3之和为短期时间尺度,IMF4到IMF6之和为中期时间尺度,IMF7到IMF9之和为长期时间尺度。

表1为各时间尺度下现货和期货收益率的描述性统计。可以看出,①所有时间尺度下现货和期货的收益率均值都接近零。各时间尺度之间的区别主要表现在波动性方面;②所有时间尺度下的峰度均高于3,这说明现货和期货收益率均服从肥尾分布;③Jarque-Bera正态性检验结果表明,现货和期货收益率均不服从正态分布;④利用Ljung-Box统计量对ARCH效应进行检验,结果表明原始收益率和不同时间尺度的收益率均具有显著ARCH效应,验证了利用GARCH模型建立现货和期货收益率的波动模型是合理的。

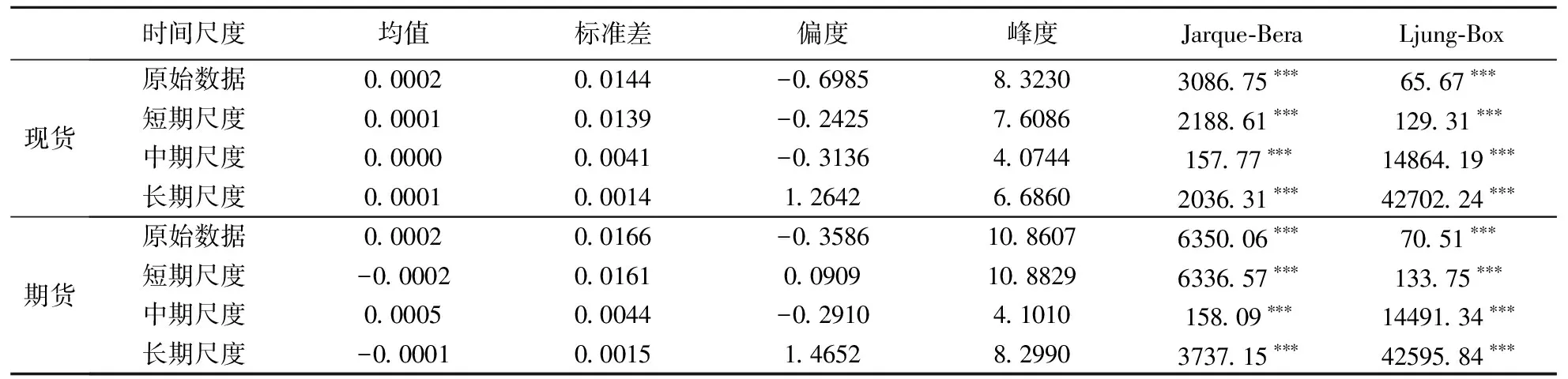
表1 各时间尺度下现货和期货收益率的描述性统计

表2为各时间尺度现货和期货收益率的方差和方差贡献率。可以看出,短期的市场波动在整个市场波动中所占份额最大,方差贡献率达到90%以上。这说明,相对于原始数据而言,短期尺度提取的波动信息是最重要的;中等时间尺度规模的方差贡献率也较大,分别为8.11%和7.16%,也可以反映较大的波动;长期尺度代表市场的长期走势,对波动率的贡献较小,在1%左右,反映股票市场的长期变化特征。

表2 各时间尺度下现货和期货收益率的方差和方差贡献率

2.3 估计套期保值比率

将整个样本区间划分为训练样本和测试样本两部分,前1946天(2010年12月31日至2017年12月28日)的数据作为训练集,后501天(2018年01月02日至2021年01月21日)的数据作为测试集,分别估算最优套期保值比率。

2.3.1 静态套期保值模型

表3为训练样本和测试样本五种静态模型的套期保值比率估计结果。可以看出,①随着时间尺度的增加,各模型估计的套期保值比率逐渐降低。原始序列的套期保值比率最高,长期时间尺度的最低,原始序列和短期尺度的套期保值比率最接近。这说明,对于原始数据而言,短期时间尺度是最重要的;②在99%,95%和90%的置信水平上,最小CVaR法所求得的最优套期保值比率相差不大,尤其是原始数据和短期尺度下的比率最相近。这说明,简单最小CVaR法套期保值在不同置信水平上的套期保值表现比较稳定;③长期尺度下VAR模型的套期保值比率为负,与其他模型的估计结果出现了较大的偏离,表明VAR模型不适用于估计长期时间尺度的套期保值比率。

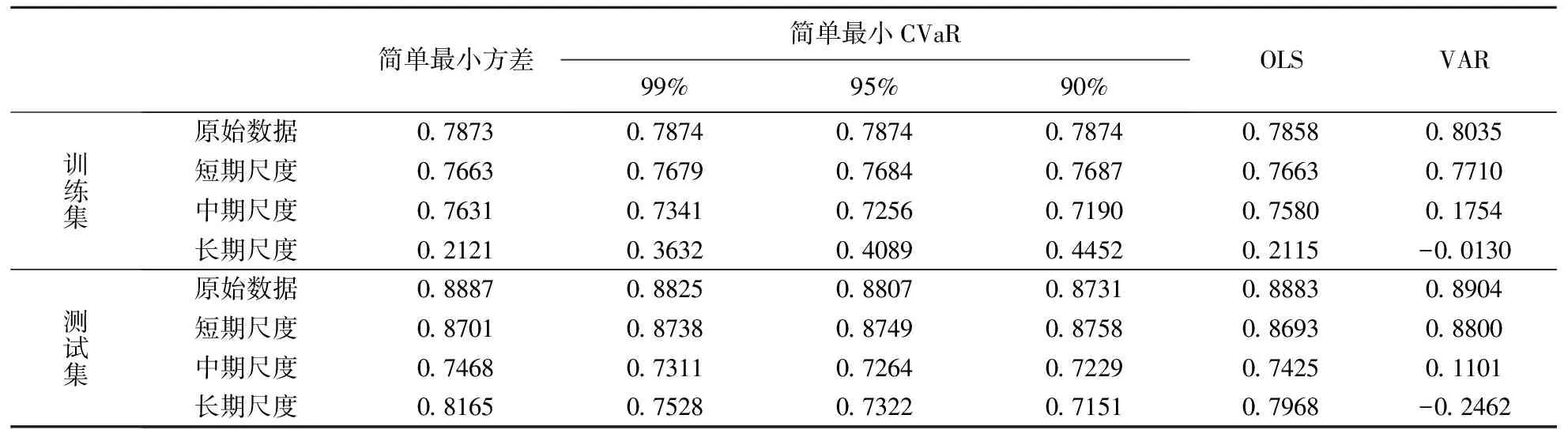
表3 静态模型套期保值比率估计结果

2.3.2 动态套期保值模型

表4为训练样本和测试样本DCC-GARCH模型的平均套期保值比率估计结果。可以看出,①原始数据的套期保值比率总是介于短期尺度和中长期尺度之间,短期尺度的套期保值比率最高,原始序列和短期尺度的套期保值比率最接近。随着时间尺度的增加,套期保值比率逐渐降低;②在长期尺度上,DCC-GARCH模型最小方差法套期保值估计结果和最小CVaR法出现了显著异常偏离;③和静态模型相比,动态模型所计算出的平均套期保值比率在原始数据和短期时间尺度上均高于静态模型的比率。

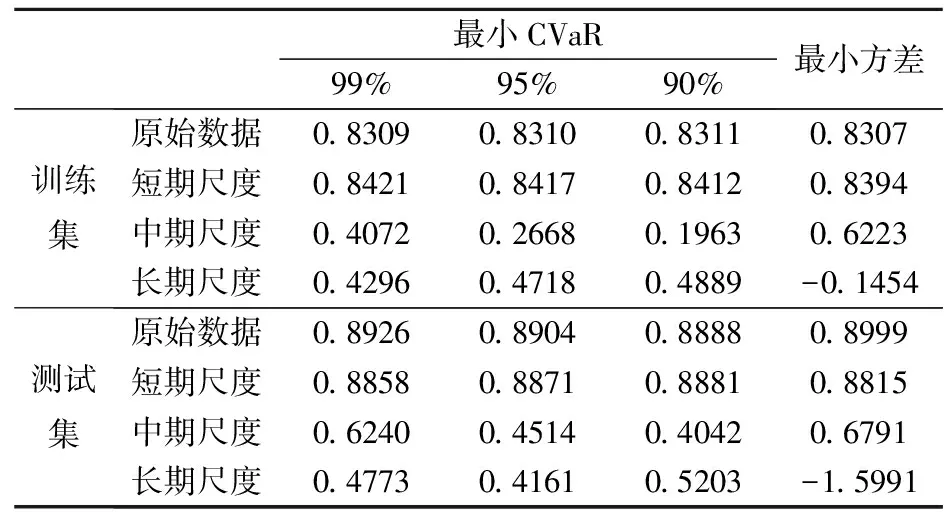
表4 DCC-GARCH的平均套期保值比率估计结果

2.4 套期保值有效性比较

分别对训练样本和测试样本下静态和动态模型的套期保值绩效进行对比,包括套期保值组合95%置信水平下的在险价值VaR和风险降低比例He。

表5、表6分别为训练样本和测试样本下各静态模型的套期保值绩效结果,由于VAR模型在训练集和测试集长期尺度下的套期保值比率均为负,故此处不再计算VAR模型在长期尺度下的套期保值绩效。可以看出,①在套期保值组合VaR方面,VaR随时间尺度增加逐渐减小,短期尺度的VaR最大,说明短期时间尺度下投资组合下行风险较大。长期尺度的VaR较小,这是由于长期尺度反映了原始数据的长期趋势,其波动性相对较小,风险也较低。在原始数据和短期尺度上,VAR模型表现最优。在各时间尺度上,利用简单最小CVaR法构建套期保值组合的VaR值均低于最小方差法的结果;②在He指标方面,随时间尺度的增加,He指标逐渐降低。训练样本中,在原始尺度和短期尺度上各模型的He指标达到80%以上,在中期尺度上除了VAR模型之外,其他模型的He指标达到60%,而长期时间尺度的He指标较低,表明在长期时间尺度上,各模型的套期保值的效果不明显;测试样本中,各模型在原始和短期尺度的He指标均达到90%以上,套期保值的效果较好。且利用简单最小方差法构建套期保值组合的He值均高于其他模型的结果。

表5 静态模型套期保值绩效(训练集)

表7、表8分别为DCC-GARCH模型训练样本和测试样本的套期保值绩效结果。从训练样本结果可以看出,①在套期保值组合VaR方面,VaR随着时间尺度的增加而逐渐减小。在原始序列和短期尺度上,相较于各静态模型,DCC-GARCH模型在降低VaR方面的表现更优。且最小CVaR法计算的DCC-GARCH模型的VaR值小于最小方差法的结果;②在He指标方面,随时间尺度的增加,He指标逐渐降低。与各静态模型相比,DCC-GARCH模型的He值较高,静态模型在原始数据的He指标只能达到83%,而DCC-GARCH模型可以达到92%,静态模型在短期尺度的的He只能达到80%,而DCC-GARCH模型可以达到89%。但该模型在中长期时间尺度下的He指标不稳定且较低,模型的套期保值效果不明显。由此可见,DCC-GARCH模型不适合于估计中长期时间尺度的套期保值。且最小CVaR法计算的DCC-GARCH模型的He值高于最小方差法的结果。

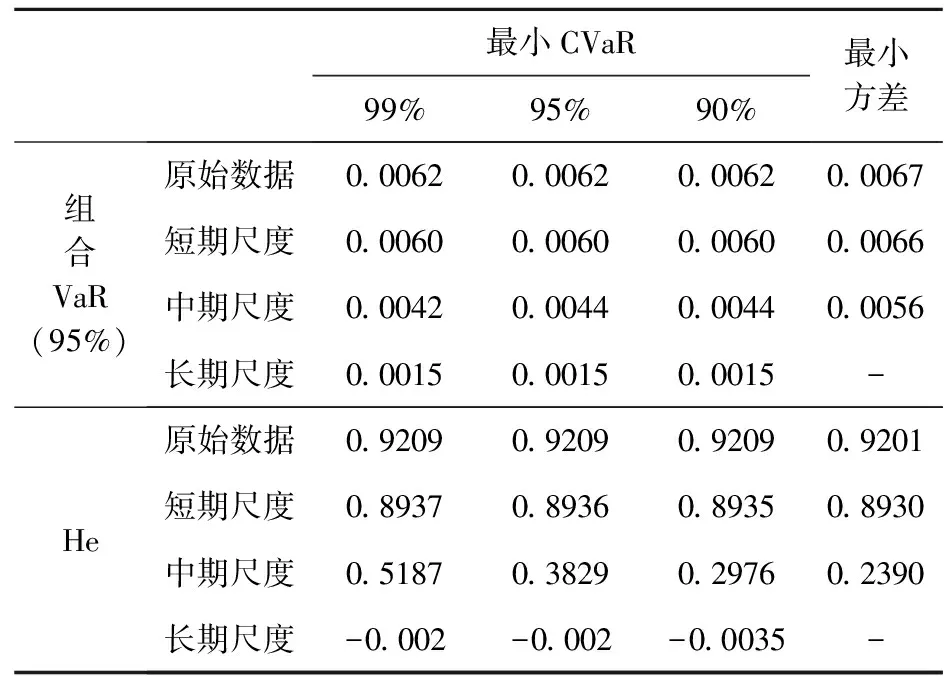
表7 DCC-GARCH模型套期保值绩效(训练集)

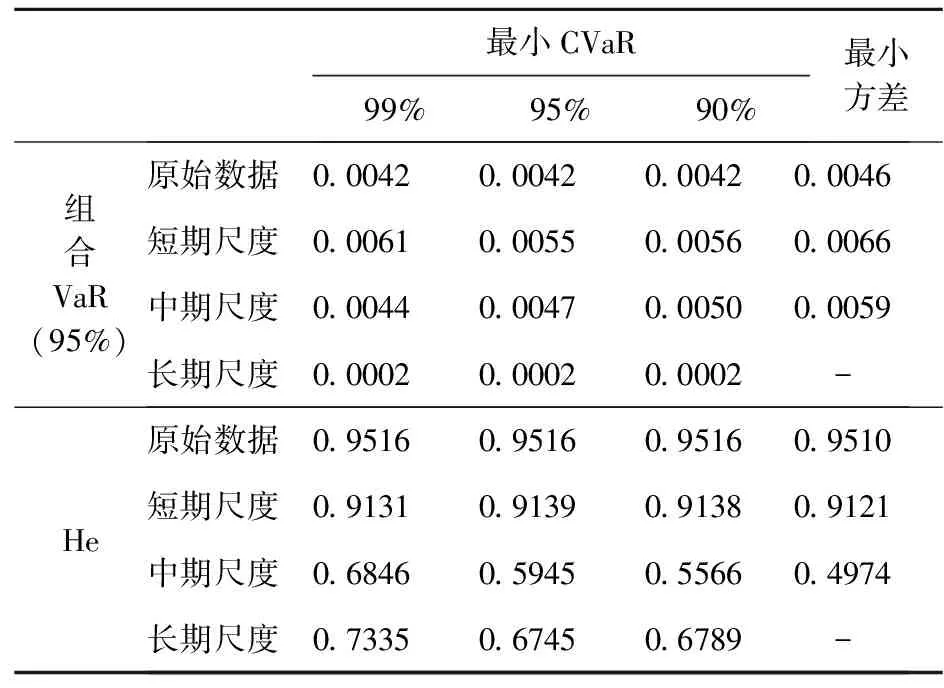
表8 DCC-GARCH模型套期保值绩效(测试集)

从测试样本结果可以看出,①在套期保值组合VaR方面,与训练样本结果一致,最小CVaR法计算的DCC-GARCH模型的VaR值小于最小方差法的结果。②在He指标方面,与静态模型相比,DCC-GARCH模型在原始数据和短期时间尺度上的表现较好。原始尺度的He值达到95%以上,短期尺度的He值达到91%以上,中长期时间尺度的He指标不稳定且较低,模型的套期保值效果不明显。且最小CVaR法计算的DCC-GARCH模型的He值高于最小方差法的结果。

3 结论

鉴于不同时间期限对套期保值问题研究的重要性,本文利用考虑时-频域的经验模态分解法(EMD)将沪深300指数现货和期货收益率分解重构为短期、中期和长期三个时间尺度,并在最小方差和最小CVaR两种套期保值策略下研究传统静态套期保值模型和动态DCC-GARCH模型的最优套期保值比率和套期保值绩效。得出结论:①原始序列和短期时间尺度下的最优动态套期保值比率走势最相似。随着时间尺度的增加,最优套期保值比率逐渐降低;②在套期保值绩效方面,动态DCC-GARCH模型在原始尺度和短期尺度的表现优于静态套期保值模型,可以显著降低组合VaR,提高风险降低比例He;静态VAR模型和动态DCC-GARCH模型不适用于中长期尺度最优套期保值比率的估计。对于DCC-GARCH模型,利用最小CVaR法计算的套期保值绩效优于利用最小方差法计算的结果。

本文在研究中均假设套期保值比率的估计参数是已知的。现实中,沪深300指数现货和期货均具有随机不确定性,其收益均值和波动率均存在估计风险。在模型参数不确定的条件下研究现货和期货间的套期保值问题,更符合真实地投资环境,具有更广泛的适用性。今后的研究方向可以考虑引入贝叶斯方法,研究模型参数不确定下的贝叶斯套期保值问题。也可以从行为金融学的角度,引入投资者的模糊厌恶心理,研究不同模糊厌恶程度下的最优套期保值策略问题。