新高考下考虑时序约束的分班规划问题研究
2023-11-06吴庆华
孙 哲, 王 翀, 吴庆华
(华中科技大学 管理学院,湖北 武汉 430074)
0 引言
2014年9月,国务院印发了《关于深化考试招生制度改革的实施意见》,拉开了新高考改革的序幕[1],之后各省也陆续发布了本省市的《普通高考综合改革实施方案》[2],规定除语文、数学、外语3个统考科目外,考生可根据兴趣特长及报考高校要求从物、化、生、政、历、地等6门(或7门,浙江多一门通用技术)学科中任选3门参加考试(该3门学科称为选考学科,剩余3门称为学考学科),相关成绩纳入高考成绩。将选择权交给学生后,学生的选课组合从原来的文理2种,变为6选3的20种(或7选3的35种,及部分省市“3+1+2”模式的12种)。新的高考选科制度,直接导致同一班级学生的选科不尽相同,这必然导致班级存在多种学科选科组合。受教学资源的限制,如果全部按照学生选科种类分班是不现实的[3],即每个班级无法开设所有的选考课程,这必然导致部分学生需要到别的班级进行插班(即走班)上课,从而形成走班制教学。国内走班制度主要有两大模式:一种是以北京十一学校为代表的全科走班(全走班);另一种是行政班与教学班并存的模式(根据走班程度分为小走班、中走班和大走班)[4,5]。本文主要针对行政班与教学班并存的模式进行讨论。
与传统的班级授课模式不同,学生需在自己所属行政班不上课的时段到某个教学班上自己所选修的课程。在实际中,走班制教学模式会使排课的约束条件增多,学校教育资源匮乏的现象进一步凸显,绝大部分高中正面临“选科难、走班难、排课难、管理难”的困境[6]。对于部分已经实施走班教学的中学,低效的分班规划和走班排课方案,不仅造成教学资源的浪费,还会导致教师教学工作量增加、学生学业负担加重、教师授课和学生学习效率降低、学校教务安排无法满足等现象,而良好的分班规划方案,可以有效解决这些问题。
对于传统的排课问题,自20世纪中期以来,国外的学者就陆续开展了研究,但文献中研究的大部分排课表问题都是以不同国家和地区的教育体制为背景,所以研究问题在基本目标、资源限制等方面存在较大差异[7]。同时,对于我国新高考下的分班规划问题,尚未发现英文文献对该问题进行研究。相比于国外,由于高考改革至今时间较短,国内对新高考走班模式下的排课算法研究也仅有少数几篇,侯发毅[8]采用UML的设计思想对新高考模式下的走班教学管理系统进行了研究,分析了选课与走班排课的需求与基本业务流程,该研究着重对选课信息进行了规划。王华鑫[9]整理了高中分层走班教学模式的基本流程,将分层走班排课问题分为分班规划与走班排课两个阶段,分班阶段使用贪心策略与对偶班制度,排课阶段使用爬山算法满足硬约束,再使用模拟退火算法优化软约束,但是在实际情况下,学生自主选科的结果会保持较大的多样性,在班级资源的限制下无法使其恰好满足对偶班制度。
本文分析了分班规划问题的特点与困难,提出了行政班分班以及教学班分班规划的数学模型,并用CPLEX求解,验证了模型的有效性。同时提出了一种变邻域搜索算法,针对教学班分班规划问题设计目标函数、邻域定义以及优化方案等,对该问题的大规模算例进行启发式求解,高效计算出优质的分班方案,以降低后续走班排课的难度。
1 分班规划问题
分班规划问题是一个多目标、多因素、多约束条件的组合规划问题,根据学生上课地点是否固定分为行政班分班和教学班分班规划问题。为了减少学生走动及便于管理[10],选考学科以外的科目如语文、数学、外语等各项教学活动往往以固定的形式安排在本班上课,只由本班的学生和教师参加,这些固定的班级称之为行政班。而对于部分选考学科,学生需要脱离其所在行政班到别的班级进行走班上课,这种临时组建的选考科目班级称为教学班[11]。
1.1 行政班分班规划问题分析
为了减少学生走动,便于班级管理,在进行教学班划分之前,会尽量将选课一致或者相近的学生编排到同一行政班级。在实际中,行政班划分一般有以下几种形式:优先三科成班、定二走一、定一走二等[12]。随着班级选科组合相同的学生越多,教学班划分的难度也会降低,所以学校需要根据自身的资源情况来确定行政班分班模式。本文给出该问题的一般数学模型。
1.2 行政班分班规划数学模型
新高考行政班分班规划问题,可归纳如下,已知学生的选科组合,该问题需要把学生指派到各班级中,若该班级所有学生都选择了某科目,则该科目视为固定形式上课,最终每个班级以固定形式上课的科目数量最多,并同时满足班级人数上下界约束。
1.2.1 变量与参数
相关参数:
I:所有学生的集合;
J:所有教室的集合,包括行政班教室J*和额外教室J′,J=J*∪J′;
K:所有学科的集合;
Sik:若学生i选择了学科k,则Sik=1,否则Sik=0,i∈I,k∈K;
Uj:教室j的人数上界,j∈J;
Lj:教室j的人数下界,j∈J;
M:一个很大的常数。
决策变量:
xij∈{0,1}:若学生i被分配到班级j,则xij=1,否则xij=0,i∈I,j∈J*;
yjk∈{0,1}:若班级j固定开设学科k,则yjk=1,否则yjk=0,j∈J*,k∈K。
1.2.2 数学模型
基于以上符号说明,建立本文的数学模型如下:
(1)
约束条件:
(2)
(3)
(4)
(5)
(6)
目标函数(1)为行政班分班规划的最优目标,即最大化班级所固定的学科数。式(2)表示每个学生只能被分配至一个行政班;式(3)表示每个班级的学生数量必须满足教室容量约束;式(4)代表每个行政班最多固定3门学科(每个学生的选科组合相同);式(5)和式(6)确保固定某门学科时,班级内选择该学科的人数必须等于班级总人数。
1.3 教学班分班规划问题分析
教学班分班规划是一个考虑时序约束的分班规划问题。我们观察到,为了最大程度利用上课时间,学校会指定某个时间段只有教学班上课,这样就得出一种名为“同时上课”的课表要求[13],而教学班分班规划就是在资源限制的条件下分出满足学生选课需求的教学班,教学班分布在不同时间段同时上课。为了每个行政班总课时数平衡,其最佳开课选择是每个班开设3门选考科目以及3门学考科目(非走班科目一致)。为了满足“同时上课”的需求,该问题需要考虑时序约束,规定这3门选考科目(选考课和学考课原理相同,本文以选考课为例进行讨论)必须分别属于3个不同且互不相交的课程组(实践中称为选考时序组)。每个时序组需要为每一位学生分配一个教学班级,并使得最终该生的3个教学班级与其所选3门学科一致,若教学班教室与学生所在行政班教室不一致,则视为走班。最终,每个选考时序组都包含全体学生,每个学生在3个组中都只属于一个和其选考科目相一致的教学班,如图1所示。对于同一时序组的选考教学班级,只要保证统一时间上课,便可以避免学生在选考课上课时间上的冲突,如图2所示。需要注意的是,为了减少学生走动,应尽量将学生分配至其所在行政班开设的选考教学班。同时,若学校有多余的教室资源,允许借助额外教室设置教学班。最后,对于不存在相互插班的选考教学班(整班),可以不受“同时上课”的约束而脱离其所在选考时序组,这样可以减少对任课教师数量的依赖。
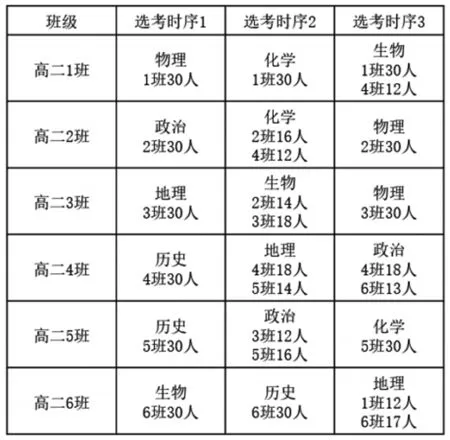
图1 教学班分班示例
教学班分班规划问题的硬约束规则如下:H1:开班人数不能高于教室容量的上限,也不能低于教室容量的下限;H2:所使用的教室不能多于行政班教室和额外教室的总和;H3:每个时序下课程的数量不能超过任课教师的数量;H4:教室必须开设学校指定的某一教室需要开设的课程。软约束规则如下:S1:走班的学生人数应尽可能少;S2:混班的数量应尽可能少。硬约束主要考虑了分班方案的可行性,需要开设的教学班级必须满足人数上下界、教室数量以及教师数量等,硬约束直接决定了教学计划能否顺利执行。需要注意的一点是,开班人数不能高于教室容量的上限这是必然的,但现实中往往会因为某一科选择人数过少而无法成班,但其实这种情况学校也是允许成班的,所以在建模的过程中,会将不能低于教室容量下限这一硬约束作为目标函数来考虑,以此来评判低于下限的程度。而软约束的设定主要考虑教学管理的难易程度,更少的人员走动,既可以降低管理难度,还可以提高后续课表调整的灵活性。所以在设计数学模型和算法时应同时考虑这两种约束。
1.4 教学班分班规划数学模型
考虑时序约束的教学班分班问题,可以归纳总结如下,给定3个时序组,对于每个班级,需要确定每个时序组内所开设的课程,行政班必须开设3门课程,额外班级可以不开设课程;对于每位学生,需指定3个对应科目的教学班,指定的3个班级分布在3个不同时序组。问题的目标是使得走班上课的人数尽可能少以及班级人数尽可能合理,同时满足教学班人数上界、任课教师数量、教室数量、必开学科等约束条件。
1.4.1 变量与参数
相关参数:
T:所有时序的集合,一共为3个时序;
Bij:若学生i的行政班级为班级j,则Bij=1,否则Bij=0,i∈I,j∈J*;
Hjk:若班级j必须开设学科k,则Hjk=1,否则Hjk=0,j∈J*,k∈K;
Ck:学科k的教师数量,k∈K。
决策变量:
xjtk∈{0,1}:教室j在时序t开设学科k,则xjtk=1,否则xjtk=0,j∈J,t∈T,k∈K;
yitj∈{0,1}:学生i在时序t走班至教室j,则yitj=1,否则yitj=0,i∈I,t∈T,j∈J;
zitk∈{0,1}:学生i在时序t上学科k,则zitk=1,否则zitk=0,i∈I,t∈T,k∈K;
pit∈{0,1}:学生i在时序t需要走班,则pit=1,否则pit=0,i∈I,t∈T;
djt∈N+(N+表示正整数):表示教室j在时序t人数不足的程度,djt取0表示教室j在时序t不开设课程或者满足最少开课人数。
1.4.2 数学模型
基于以上符号说明,建立本文的数学模型如下:
(7)
(8)
约束条件:
(9)
(10)
(11)
(12)
(13)
(14)
(15)
xjtk+yitj-1≤zitk,∀i∈I,∀t∈T,∀j∈J,∀k∈K
(16)
yjtk+zitj-1≤xitk,∀i∈I,∀t∈T,∀j∈J,∀k∈K
(17)
pit≥yitj-Bij,∀i∈I,∀t∈T,∀j∈J
(18)
(19)
(20)
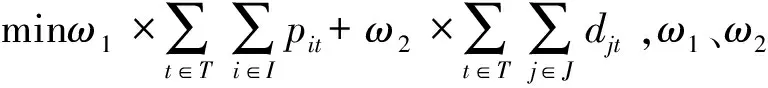
2 算法设计
2.1 构造初始解
本文中的可行解由两部分组成:(1)xjtk表示每个班级在每个时序所开设的课程,若j是行政班,则只需考虑需要开设哪一门课程,若j是额外教室,则还需考虑是否开设课程;(2)决策变量yitj和zitk用来描述每个学生在每个时序走班的教室以及所上的课程。本文采用随机贪婪的思想来构建初始解,具体步骤如下:
步骤1确定xjtk,先根据参数设置的班级必开学科放置课程,再随机选取直至每个班级3个时序都分配了不重复的学科,随后通过爬山算法优化3个时序内的学科分布,使得每个学科尽可能均匀地分布在3个时序。
步骤2初始化学生3个时序内的上课顺序(zitk),通过贪心策略计算学生选课组合与每个班级开课组合的匹配度进行分配,如班级开课组合顺序为物、化、生,学生选课的也为物、化、生,则匹配度为3(完全匹配),优先将该学生分配至该班级的三个时序。若最大匹配度为2,则还需在不匹配的时序内随机选择一个学科匹配的新班级,以此类推,确定yitj。
2.2 变邻域搜索算法(VNS)
变邻域搜索(Variable Neighborhood Search,VNS),由MLADENOVIC和HANSEN[14]提出,本文设置了四个邻域对初始解进行局部搜索。从随机构造初始解开始,通过四个邻域的迭代搜索,并在每一轮搜索完成后保留当前最优解(中间解)进行优化,通过多次重启的方式,代替VNS常用的扰动,更新当前最优解。最终,通过Itermax次搜索得到最优解(最终解)后,进一步优化以更精确地计算约束满足情况,算法伪代码如下。

表1 多次重启的变邻域搜索算法步骤
2.2.1 移动操作与邻域
为了有效搜索解空间,本文提出了4个邻域操作:N1(FlipClass),N2(SwapTwoClass),N3(ExchangeClass)以及N4(ExchangeCombination)。每次迭代以遍邻域的方式从当前邻域选择最佳移动,并保留为当前解S′,若当前解f(S′) N1(FlipClass):将任一班级j在时序t的科目k1,更换成学科k2。以图1为例,高二(1)班在时序1开设物理,变更为开设生物。 N2(SwapTwoClass):交换同一时序t中的任意两个班级j1和j2所开设的学科k1和k2。以图1为例,时序1中高二(1)班开设物理,高二(2)班开设政治,交换后,时序1中高二(1)班开设政治,高二(2)班开设物理。 N3(ExchangeClass):交换任一班级j在时序t1和t2内的学科k1和k2,并交换该班级作为行政班所包含学生的上课顺序。以图1为例,高二(2)班开设学科为政、化、物,交换时序1、2后为化、政、物,同时学生上课方案也一同交换,高二(2)班共有两种组合的学生,上课顺序为政、化、物和政、生、物,交换后为化、政、物以及生、政、物。 N4(ExchangeCombination):交换任一班级j某一选科组合的学生在时序t1和t2的上课顺序。以图1为例,高二(6)班存在两种选科组合的学生,上课顺序分别为生、历、地及生、历、政,交换时序2和时序3中的上课顺序,则变为生、地、历和生、政、历。 值得注意的是,每一次邻域操作主要针对xitk和zitk设计,并根据变换过的xjtk和zitk更新yitj,再计算该操作导致的目标函数惩罚值的变化。同时,我们仅考虑班级开设学科和不同选课组合上课顺序的变化,并不以单个学生为单位,大大缩小了邻域空间,提高了搜索效率。 2.2.2 对中间解及最终解的优化 搜索得到的中间解需要进行优化,目标是改善违反人数下界约束的程度。在不改变班级开设学科的前提下,以单个学生为单位(邻域搜索中以选课组合为单位进行搜索),交换单个学生的上课顺序或改变单个学生在每一时序上课的班级,平衡班级人数。完成全部搜索得到最终解后,继续调整单个学生,需要考虑的目标有使各教学班人数尽量平均,检查并调整是否有本班开设了对应科目学生却走班至其他教室上课的情况。 本文通过数值算例来说明问题性质及VNS算法的表现。其中采用C++编写VNS算法,所有试验均在Intel Core i5-8400 @ 2.8GHz 64位计算机上进行。由于国内现有对新高考分班规划问题的研究较少,无法找到现有的基准数据,因此本文使用广州某中学高三年级的数据进行实例分析,同时为了实验完整性,还使用了一组随机生成的数据来测试算法的性能与效果。 实例数据来自广州某中学高三年级的走班需求调研。该高中可选学科为6门,学生以“3+1+2”的模式进行选科,即物理和历史必须2选1,再从余下4门中任选2门。该年级一共588名学生,分为12个行政班,物、化、生、政、历、地任课教师的数量分别为5,4,5,2,2,3名,另外还拥有2个额外教室,每间教室最多容纳学生58人,最小成班人数为35人。按照学生的选课结果,已经以定二走一的模式完成行政班分班。 由于问题规模较大,无法通过CPLEX求解,所以利用变邻域算法得出具体的走班方案,如表2所示,其中“课程”表示该时序各个班所开设教学班的课程,“人数”表示该时序参加该教学班的学生人数,“混班”表示该教学班的学生组成来自除本班外的班级数,0表示整班上课。整班上课的教学班可以不参与走班,所上课程作为行政课程处理进行排课。整班上课的教学班越多,排课的难度越小。所有教学班满足人数上下限,总计非整班数量为9。该方案在满足硬约束的同时,保证了班级人数在合理区间内,且整班数量足够多,对应学科教师的任课安排将更加灵活,每个教学班混班数量不超过3个班级,降低了学校走班教学管理的难度,且原有的12个教室完全可以满足上课要求。 表2 广州某中学高三年级走班方案 本文还以实际算例为基础,随机构造了一组数据,学生规模从45到900不等,测试算法在不同问题规模与资源限制情况下的表现。表3展示了VNS和CPLEX求解器之间的结果比较,该求解器用于解决第2节中介绍的线性规划公式。Opt表示通过CPLEX求解得到的最优值。VNS表示通过VNS算法对算例进行10次计算得到的最优值。CPU表示CPLEX和VNS的计算时间。GAP表示VNS算法与最优解之间的差距。列2-列4表示问题的规模大小。从表3得出,前10组的数据CPLEX可以在1h之内计算出结果,而第11组的数据虽然在学生规模上相同,但由于多了2个班级以及1个额外班,CPLEX却花费了20倍的时间才求得最优解,这也说明了教室数量的多少对解空间影响很大。对于VNS算法来说,从计算结果来看与精确解结果相近,且基本能在1s内得到结果,这在实际应用中有很大的优势。 表3 CPLEX求解结果与VNS算法结果比较 为了进一步验证本文算法的优越性,对余下算例进行求解。表4展示的是VNS在较大规模算例上的结果。目标值是该算法对算例进行10次求解,得到的最优解。目标值的计算方式为Distlb×5+Moves,其中Distlb是该结果中教学班开班人数下界未满足的人次,Moves是该结果中学生需要进行走班的总人次。从表4可以看到,VNS平均可以在0.1s左右就获得结果。当算例规模较小时,由于已有的行政班教室资源较少,无法满足学生多样的选课需求,可能会出现硬约束无法满足的情况,所以就会优先牺牲软约束来满足硬约束,这就导致了需要更多的额外教室,且走班人数的比例会更多,以及教学班的开班人数下限难以满足。但随着学生数量以及班级数量的增加,学校有了充足的教室资源后,几乎不需要额外教室开设教学班,且走班人数的比例也明显下降,教学班的开班人数基本可以满足上下限。 表4 VNS算法结果 本文介绍了新高考下分班问题的研究背景,简述了分班问题的类型、难点及重要性。从中总结了行政班分班问题,并给出了基础数学模型。又重点介绍了考虑时序约束的教学班分班规划问题,首次提出了以开班人数最合理以及走班人数最少为目标函数的整数线性规划模型。该模型充分考虑了教学班分班的特点,例如学校的教室资源、教师资源等。然后利用CPLEX在小规模算例上进行求解,验证了模型的有效性。并设计VNS算法求解教学班分班问题。该算法在小规模算例上与CPLEX求得的最优解差距较小,在大算例上均能在短时间内获得优质解。未来可以考虑分层模式下以及基于师生最佳匹配的分班规划和走班排课问题研究。3 算例分析
3.1 实例分析

3.2 随机数据结果分析


4 结论
