考虑障碍物遮挡和雷达衰减的VTS雷达站选址优化研究
2023-11-06艾云飞
黄 川, 吕 靖, 艾云飞
(1.大连海事大学 交通运输工程学院,辽宁 大连 116026; 2.中国交通通信信息中心,北京 100011)
0 引言
船舶交通管理系统(Vessel Traffic Service,VTS,后文简称VTS系统)自建立以来,在降低水上交通事故数量、提高船舶通航效率发挥了重要作用,但是目前随着船型大型化和船舶数量的不断增加,需要进行额外监控的水域数量也在飞速增长,因此有必要增加VTS系统数量确保水上交通安全进行,而雷达站作为整个系统的核心部分,其位置选择对整个系统的效率发挥有至关重要的作用,因此有必要对VTS雷达站选址进行科学研究。
目前国外研究主要专注于VTS相关的立法法规[1]、VTS系统运行的可靠性分析[2]、VTS系统建设的经济效益分析[3]和VTS系统的发展需求研究[4]等方面,对于VTS雷达站选址的研究较少,考虑到VTS雷达站选址属于设施选址问题,因此对水运其他研究对象选址进行研究,主要包括应急物资储备库[5]、干港[6]等。国内关于VTS雷达站选址的研究主要有:曹德胜等[7]从多个方面构建VTS雷达站候选点评价体系,然后基于集合0-1覆盖模型构建单目标选址模型。艾云飞等[8]在此基础上将雷达站配型和VTS中心选址因素考虑在内,构建双目标模型和双层模型并设计遗传算法求解。黄川和吕靖[9]提出了水域精细划分方法和水域风险评价指标体系,基于ArcGIS软件相关功能构建了VTS雷达站双目标选址模型。
可以看出目前大部分研究只是关于VTS系统雷达站选址本身构建模型进行求解,而并没有将建站环境中的相关因素考虑在内,本文在此基础上对实际环境中山脉、森林等实体遮挡及雷达无线电波在介质中传播存在衰减两个因素进行考虑,而目前国内外关于环境中遮挡因素的研究主要有遮挡环境下BDS/GPS的定位性能分析[10]、抗环境遮挡的目标跟踪算法研究[11]等。关于雷达无线电波传播衰减则主要集中于雷达衰减订正[12]、雷达衰减补偿[13]等。目前关于这类选址模型求解算法国内外研究较多,主要分为精确解算法和启发式算法,精确解算法主要包括分支定界法、列生成算法[14]以及两者组合形成的分支定价法等,启发式算法则包括遗传算法、蚁群算法等。
综上所述,目前对于VTS雷达站选址主要集中于集合0-1覆盖进行研究,对于选址环境及其他因素考虑较少,因此本文考虑建站环境中的遮挡以及雷达无线电波传递衰减因素,同时对每个水域进行备择覆盖以防出现当雷达失效时水域无法被监控的问题,基于集合覆盖构建VTS雷达站选址模型,使得项目总建站成本最小和水域面积总覆盖率最大,并设计自适应权重多目标粒子群算法进行求解。
1 问题描述与模型构建
1.1 问题描述
考虑到雷达环形搜索的工作特性,因此本文主要基于集合覆盖模型研究在存在障碍物遮挡和雷达传递衰减情景中如何进行VTS雷达站最优选址,同时在建址过程中对雷达站建站点高程、雷达站建站高度、水域高程、单个雷达失效和环境遮挡物等予以考虑,具体示意图如图1所示。

图1 VTS雷达站示意图
在图1中,整个建站环境空间大小为x,y,z∈[0,10],图中X和Y轴构成平面模拟为地球基准平面,Z轴为垂直高度,Z轴数值代表模拟高程数据,在该环境中存在山体障碍物ABCD和4个需要被监控的水域,在此环境中考虑单个雷达失效时进行VTS雷达站选址。
1.2 逐渐覆盖函数
本文引入逐渐覆盖函数进行雷达衰减测度,从而在无线电波随距离衰减的情况下研究雷达站对于水域监测概率的变化情况,水域被覆盖率区间也从传统的0-1二元区间变为[0,1]区间,常用逐渐覆盖函数如图2所示。
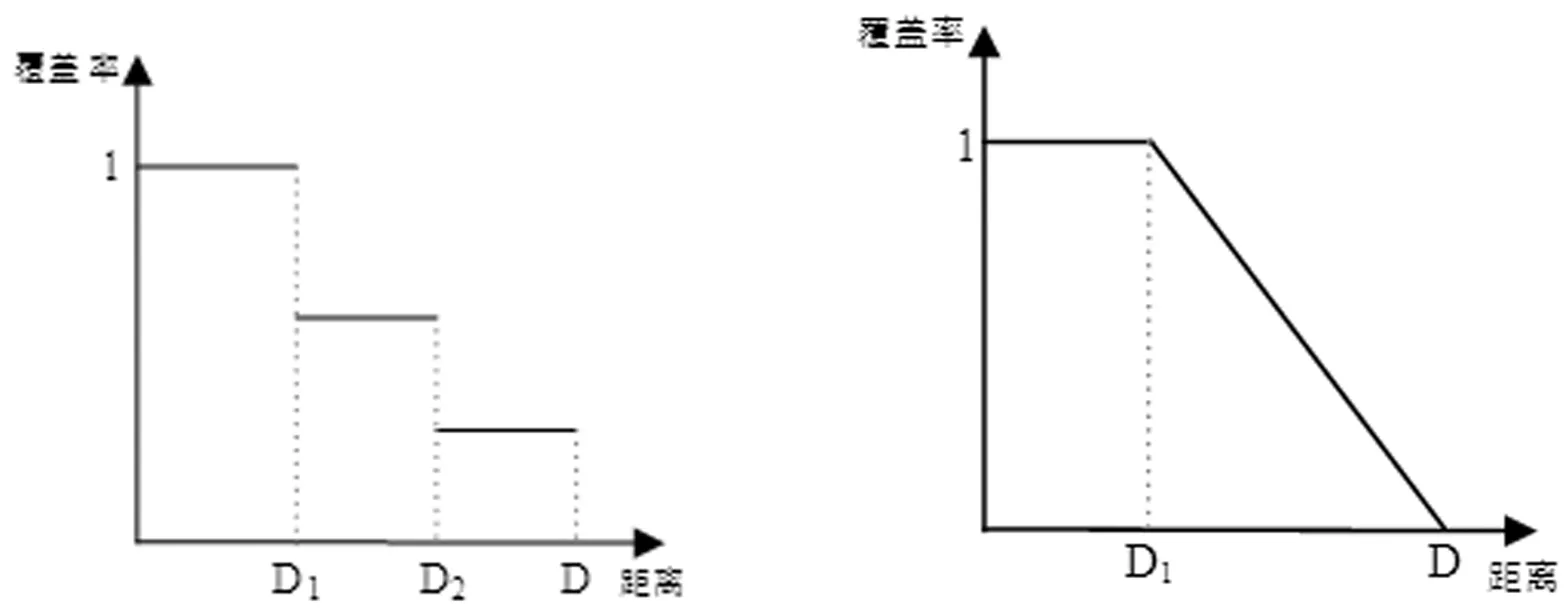
(a) (b)
1.3 障碍物遮挡覆盖率计算方法
本节进一步在考虑障碍物遮挡情况下结合候选站点和水域间的距离和1.2节的逐渐覆盖函数计算雷达站点对于监测水域的覆盖率。
(a)当雷达站与水域间距离不在雷达作用范围内时,即雷达站对于该水域的覆盖率为0;(b)如果两者间距离在雷达作用范围内且有障碍物遮挡时,则依据距离和逐渐覆盖函数计算得到覆盖率,在此基础上乘以一个[0,1]间任意数的穿透率;(c)如果两者间距离在雷达作用范围内且无障碍物遮挡时则以两者间距离和逐渐覆盖函数进行覆盖率测算。
现对情况(b)下覆盖率计算过程进行详细说明。在图3中存在障碍物T-RSQ和P-MON,水域8,目前拟建立雷达站KK。本文在计算过程中是以雷达站和水域的连线与锥体构成的所有平面计算交点来验证障碍物是否形成遮挡。数学计算过程如下。
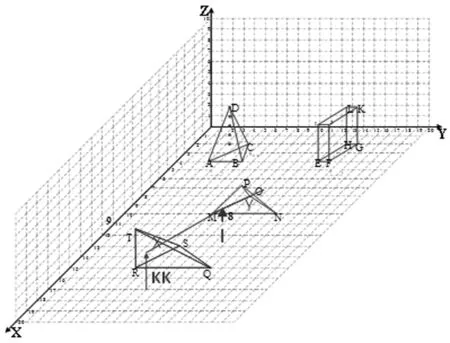
图3 遮挡示意图
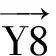
1.4 模型构建
(1)模型假设
1)优化决策过程中外部环境将保持不变。
2)障碍物的数量和穿透率以及逐渐覆盖函数公式已知。
(2)参数定义
决策变量:
yj为0-1变量,若雷达站候选点j被选中,则yj=1,否则yj=0。
模型参数:
Ai表示需要覆盖的水域,i=1,…,I,ξi为每个水域需要被覆盖的次数,μi为每个水域的面积覆盖率,Si为每个水域的水域面积,S为所有水域的总面积。
Bj表示雷达站候选点,j=1,…,J。
Cij为覆盖率矩阵,由逐渐覆盖函数f(D)和障碍物穿透率Og计算得出,D为所需覆盖水域与雷达站候选点的欧氏距离。
Fg为建站环境中存在的障碍物,g=1,…,G,Og为对应障碍物的穿透率。
Mj为雷达站候选点j的固定建设成本。
Ek为配置k型雷达的成本,k=1,…,K。
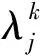
(3)模型构建
本文的双目标选址模型目标函数为:
(1)
(2)
约束条件为:
ξi≥2
(3)
(4)
(5)
(6)
(7)
目标函数(1)表示雷达站建站总成本最小,第1部分雷达站建站成本,第2部分为雷达配置成本;目标函数(2)表示监管水域面积覆盖率最大。约束条件(3)表示为了减弱单个雷达失效带来的影响每个水域最少需要被覆盖两次;约束条件(4)表示水域面积等式;约束条件(5)表示每个选中的雷达站候选点只能配备1种雷达;约束条件(6)表示如果水域被覆盖一次或多次,则至少应该建一个或多个雷达站,否则不建;约束条件(7)表示0-1变量约束。
2 算法描述
2.1 算法流程
本文采用自适应权重多目标粒子群算法对模型进行求解,权重变化公式如(8)所示,算法流程如图4所示。在进行粒子适应度计算时,中间涉及到雷达站对水域的覆盖率计算这一步骤,具体运算逻辑已在图中进行说明。

图4 算法流程图
(8)
2.2 算法有效性验证
为了全面地评价算法有效性,本文引入ZDT系列函数进行测试,采取其中ZDT1,ZDT2和ZDT6进行算法性能测试,设置相关参数,得到结果如图5-图7所示。可见该算法在ZDT测试函数集上取得了较为光滑和均匀的Pareto前沿,可以看出改进后的多目标粒子群算法能够有效获得目标问题的Pareto前沿,且非支配解具备良好的分布性,因此可以得出改进后的算法是可行有效的。
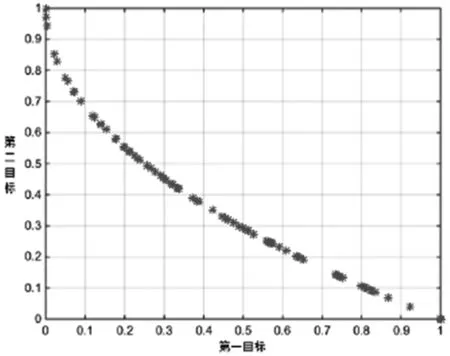
图5 ZDT1结果
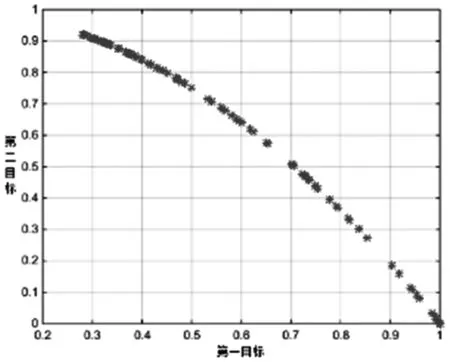
图7 ZDT6结果
3 案例分析及讨论
3.1 案例分析
本文以某省份的VTS雷达站选址项目为研究对象,将其简化为本文所需算例。整个选址示意图如图8(a)所示,在整个建站环境中存在若干分段河流,如图中红色曲线所示,同时存在山体障碍物D-ABC、P-MON和T-SQ,以及森林障碍物IJKL-GHEF。将这若干分段河流中风险较高的重要水域进行提取最终共选择10个水域,如图8(b)所示,这10个水域的具体坐标、高程及水域面积如表1所示。
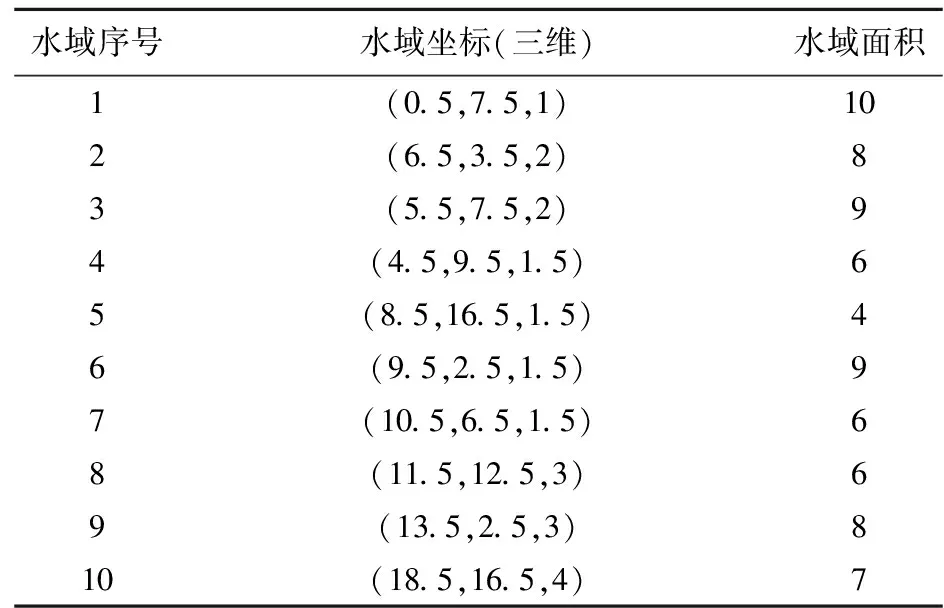
表1 水域相关信息
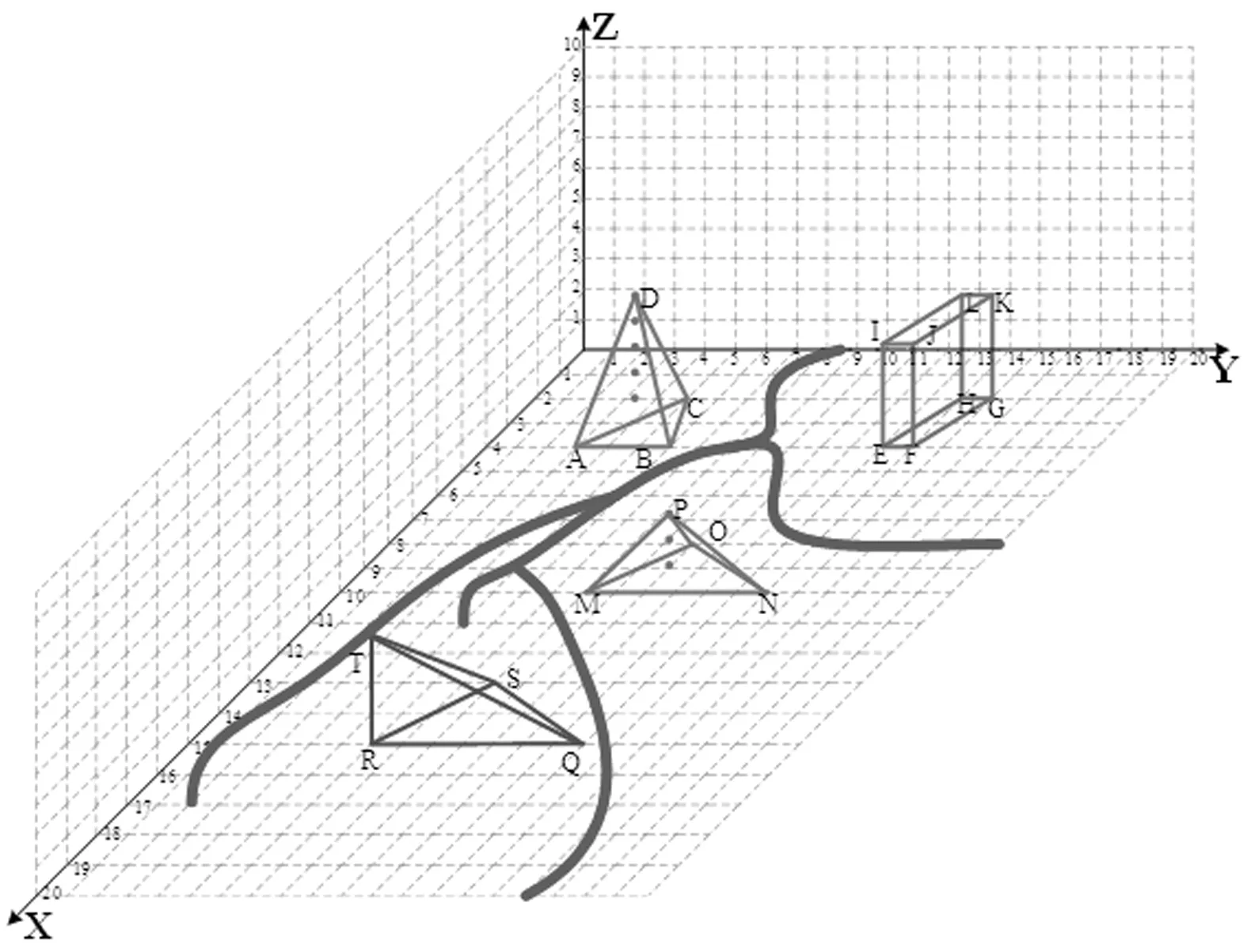
(a)
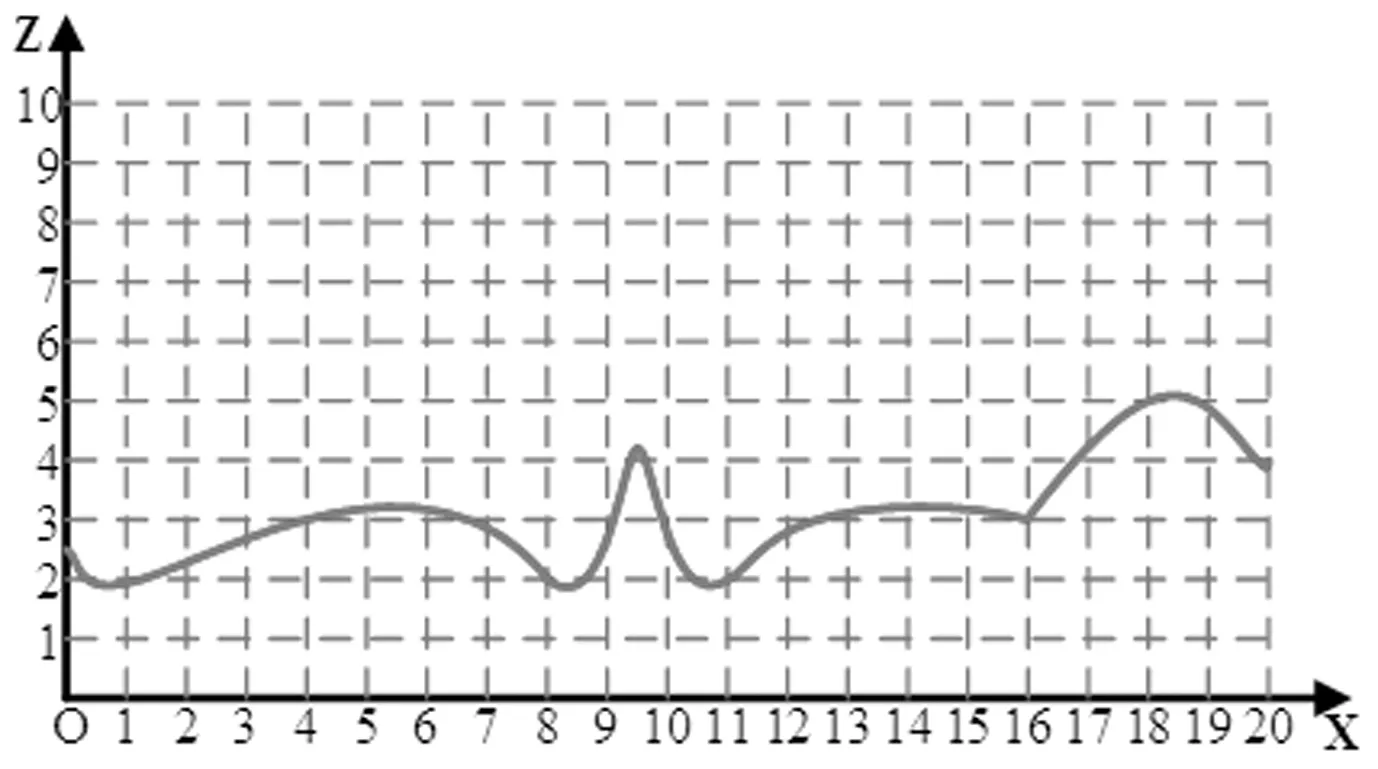
如1.3节所述,当雷达传递遇到被障碍物遮挡住情况时可以认为覆盖率为0或者将正常得到的覆盖率乘以障碍物穿透率获得在有障碍物遮挡情况下的覆盖率。本案例采用障碍物穿透率方法进行障碍物遮挡效果测算,从事实角度出发一般山体的穿透率明显低于森林障碍物,故本文假定各障碍物穿透率如表2所示,各个障碍物坐标及高程也一并给出。本文的雷达站候选点范围为三维空间中任意整数点。假定地势的高程变化截面图如图9(a)所示(垂直于Y轴得到),因为高程值为持续变化状态,为计算方便和更贴近实际,将各点高程值变化为图9(b)所示,故各雷达站候选点的实际高程值均可由此得到;另外假定雷达站的建站高度的高度为1,当某点被选中建站时,该点的高程值计算为该点地理高程和建站高度之和,否则为该点地理高程;故在考虑这些因素后整个项目中雷达站选址建站的选点范围为XYZ∈{(0,0)-(20,20),Z=各点高程值}的任意整数点。雷达参数设定如表3所示,选择图2(b)类逐渐覆盖函数进行雷达无线电波衰减测算,公式如式(9)所示。为防止因为单个雷达站失效水域无法被监测的情况出现,所有水域需要被覆盖2次及以上以实现雷达站对水域的备择覆盖。
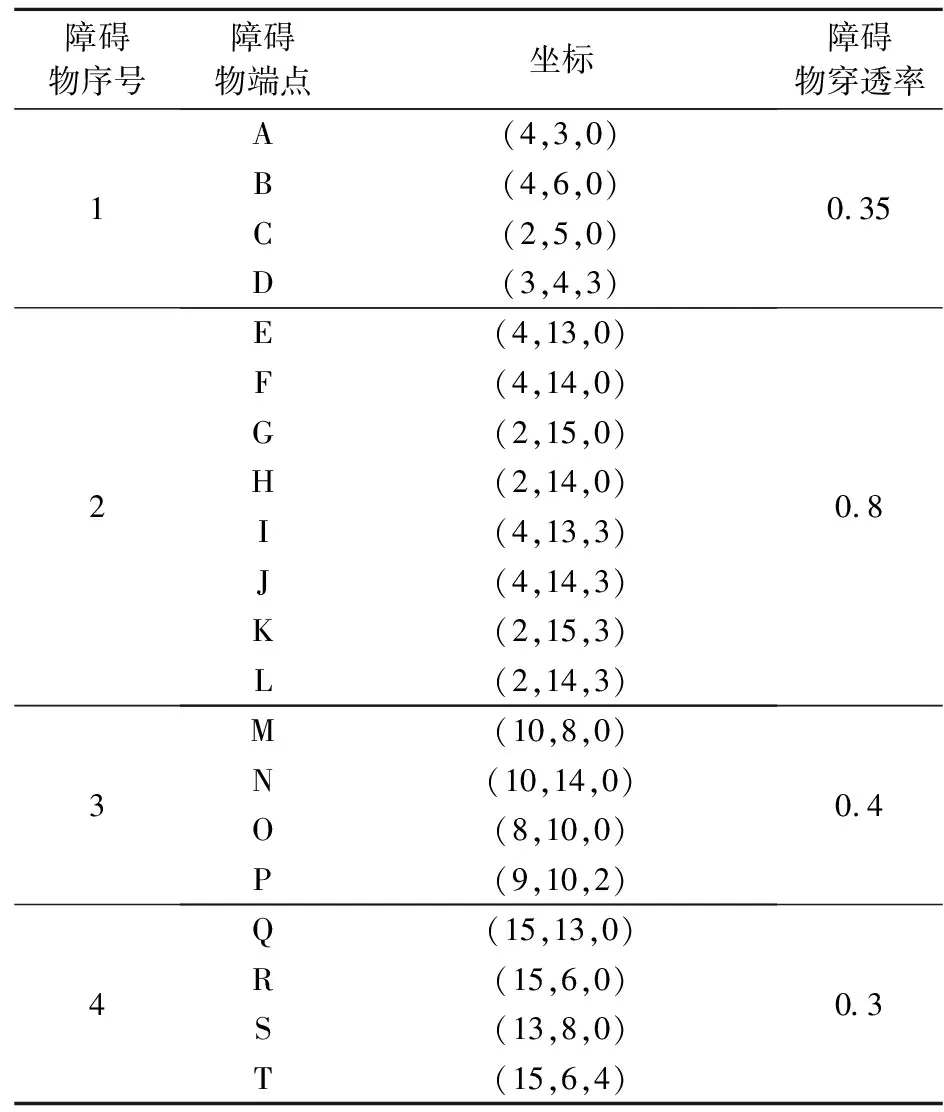
表2 障碍物相关信息

表3 雷达种类
(a)
(9)
在此实例中进行粒子初始化,考虑到需要监管的水域总数为10,故雷达站总数需小于10,因此雷达站建站数量在[5,9]内波动,雷达站建站成本假定为500;本文在处理双目标函数过程中为方便进行支配关系比较将适应度函数变为[H,10-X];覆盖率计算按照1.3节覆盖率计算方法和2.1节进行程序设计;粒子群大小设置为100,迭代代数为100,粒子维度为441,变异概率为随机数变异,外部存档数量上限为50,对于不满足覆盖次数和面积覆盖需求的粒子施以[X+P,10-Z+P],P=10^8,从而让其一直处于被支配地位,降低进入非支配解集的概率。
经过计算Pareto前沿如图10所示。在最终求得的外部解集当中设置粒子出现概率参考值,得到出现概率高于参考值粒子群并根据轮盘赌规则选取相对最优解,已在图10中用方框标出,根据最优解得出最终选址方案的总成本为6700,选中的8个雷达站候选点对于全局10个水域的总面积覆盖率为84.86%,最终确定建址的雷达站候选点分布如图11所示,用圆形代表。各建址雷达站候选点坐标及所配置雷达种类如表4所示。
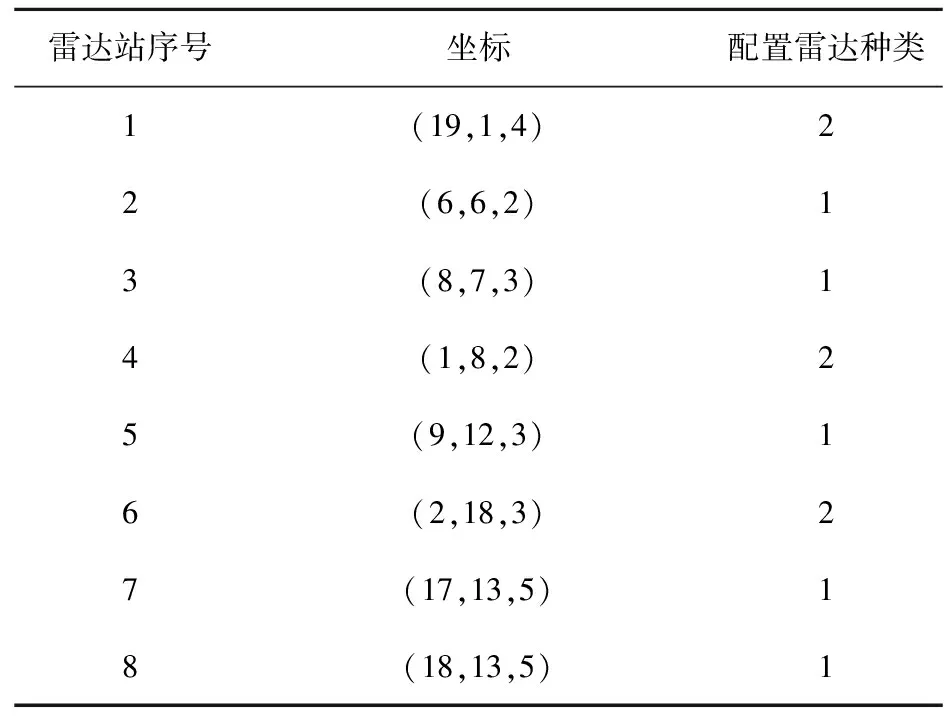
表4 雷达站坐标及雷达配置
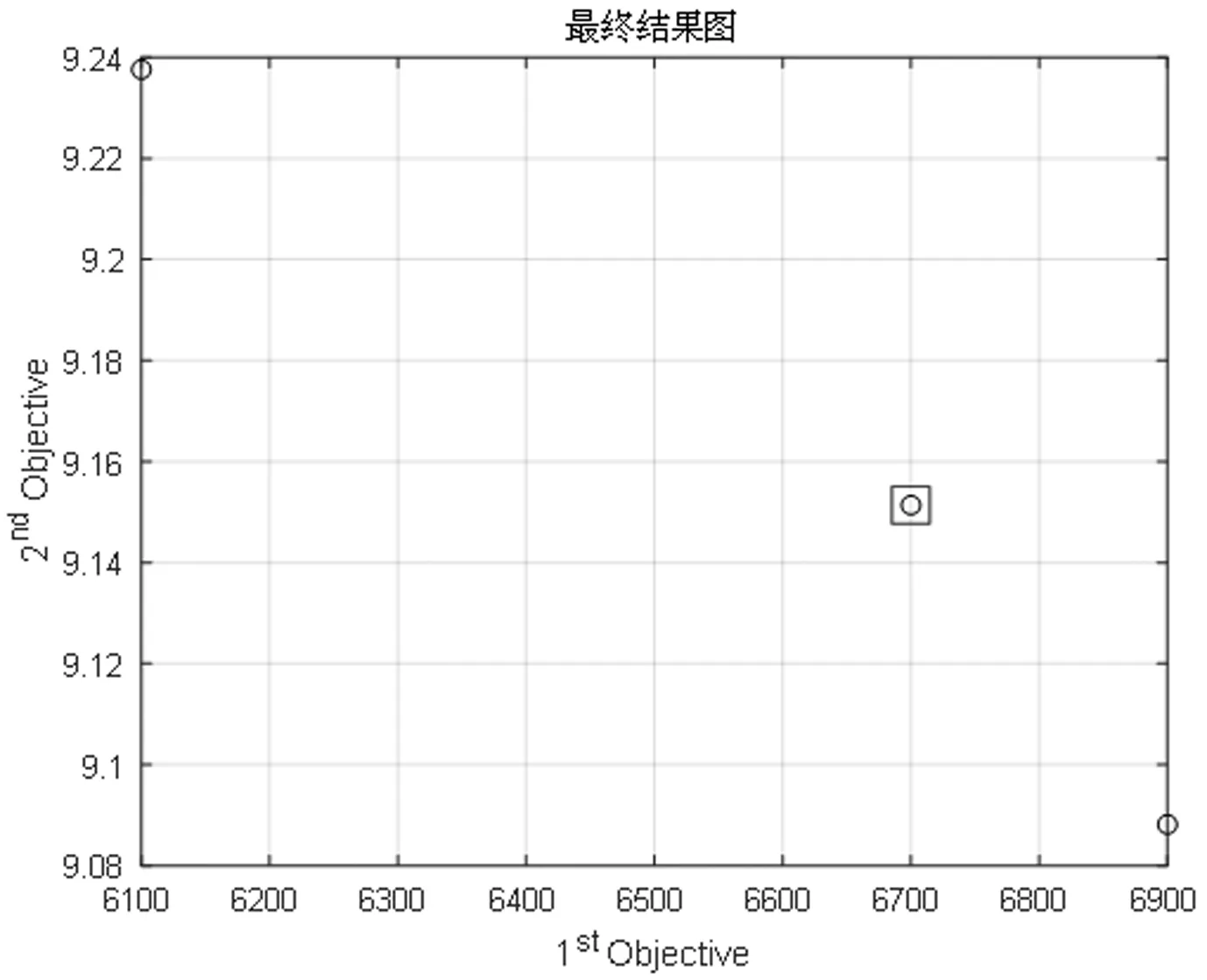
图10 案例Pareto前沿
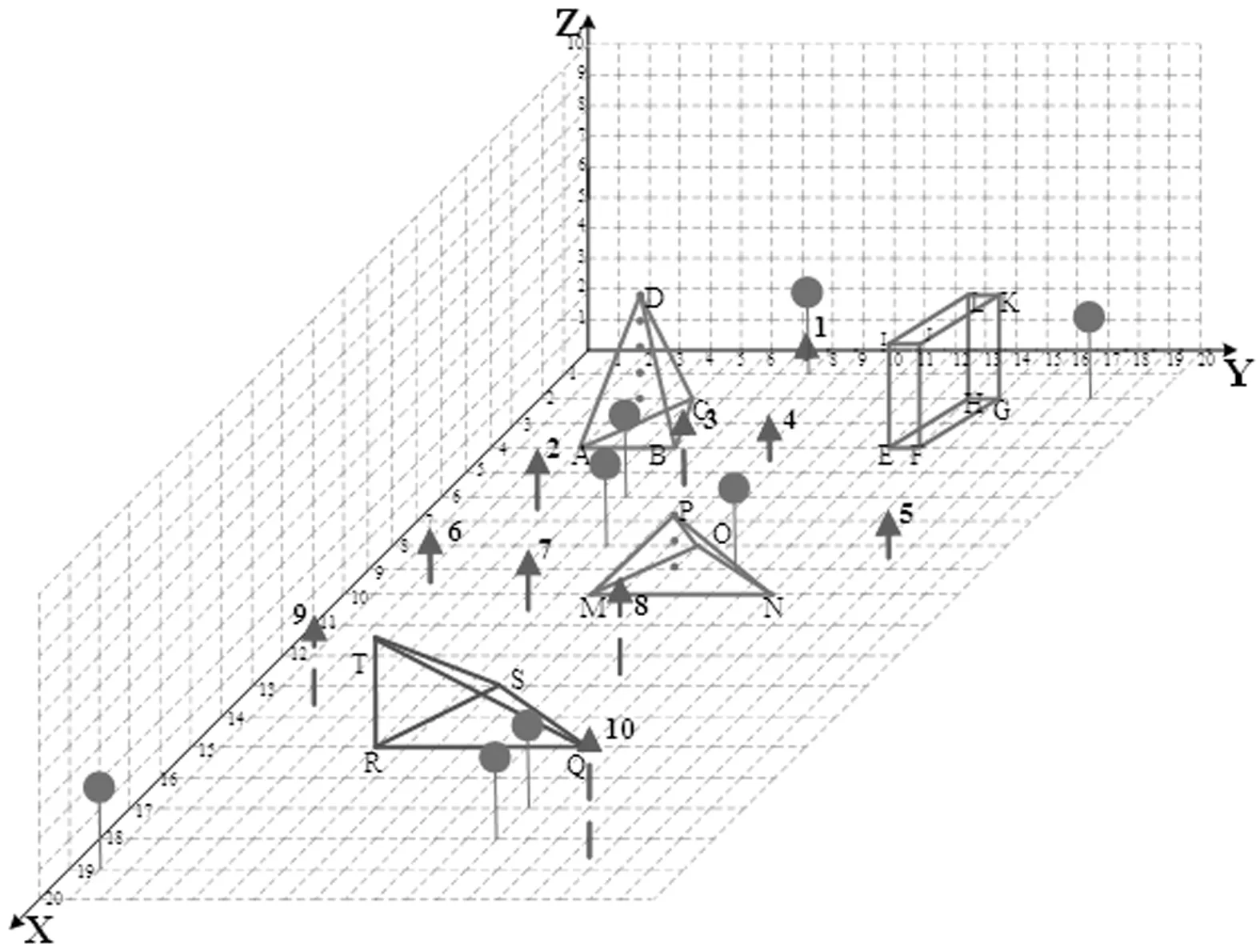
图11 选址结果
3.2 敏感性分析
观察案例分析最后所得结果可以看出Pareto前沿的选址方案中雷达站数量区间为[7,8],而案例分析在粒子初始化所设置的雷达站数量区间为[5,9],在最终帕累托前沿并没有出现其他数量的非支配解,通过对算法及参数设置进行分析,本文认为没有数量5和6的非支配解可能是由于覆盖半径和逐渐覆盖函数导致,没有数量9的非支配解则因为初始解多样性不够,而对于不同种类覆盖函数因为最小和最大覆盖半径设置数值一样,因此不同的覆盖函数只会获得不同的目标函数数值,而不太可能造成解的缺失,且经过对案例多次的Pareto前沿计算,所有前沿均没有出现数量5和6的非支配解,因此认为是由于覆盖半径和约束导致在数量5和6出现无解的情况,因此本节从覆盖半径进行敏感性分析,算法环境和前面案例一样,最大覆盖半径分别设置为7和9,最终结果如表5所示,帕累托前沿图如图12和图13所示。
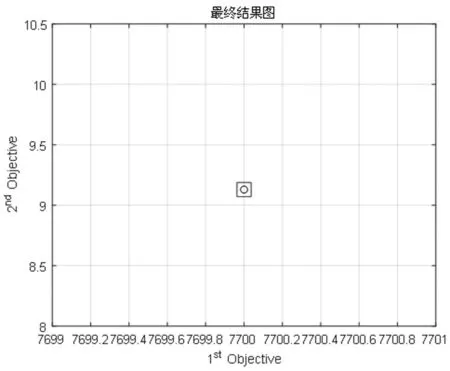
图12 最大覆盖半径为7的Pareto前沿
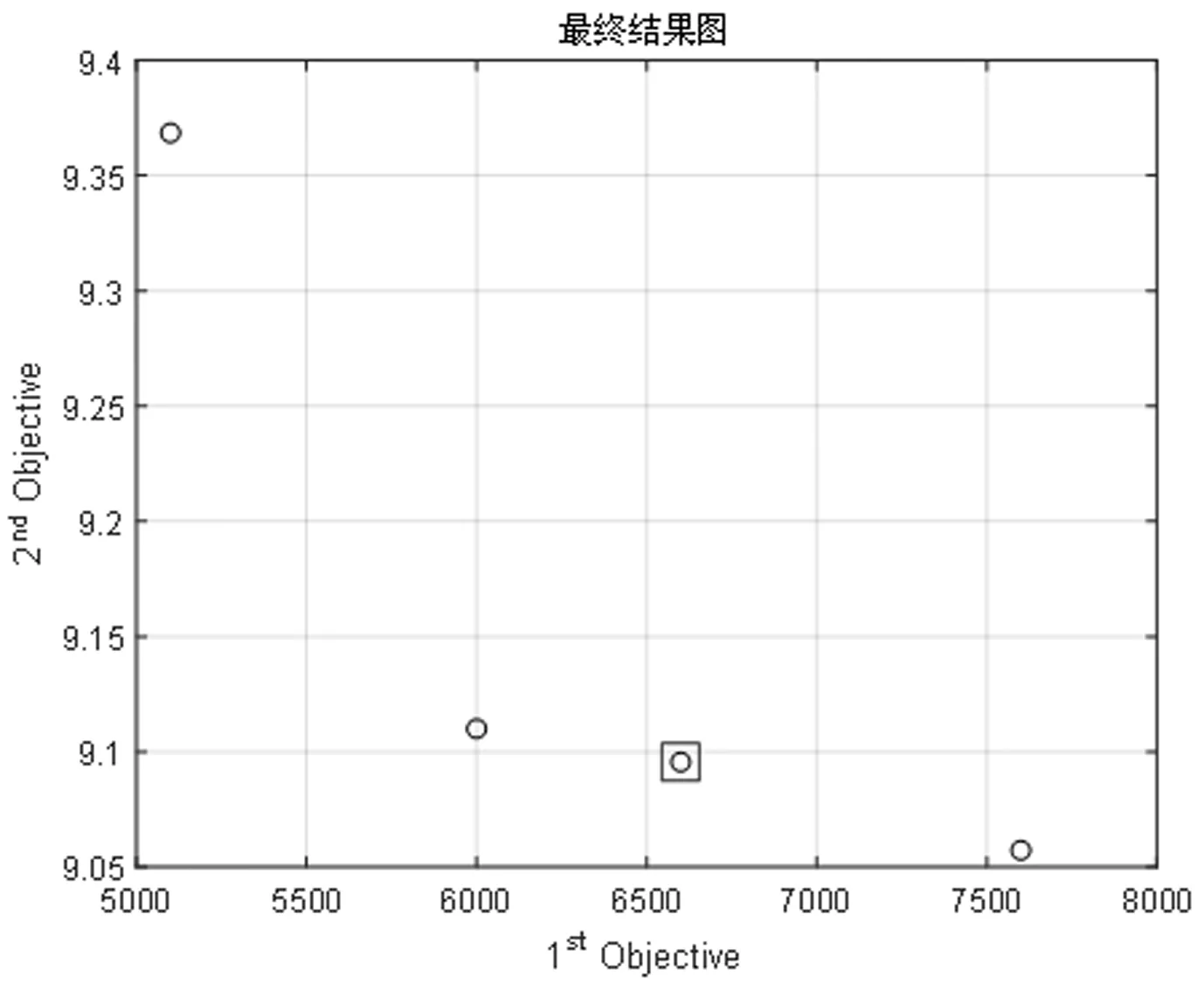
图13 最大覆盖半径为9的Pareto前沿
从分析结果可以看出,当最大覆盖半径为7的时候,最终获得非支配解较少,总建站成本为7700,对全局10个水域实现了86.97%的覆盖,需要建9座雷达站,而非支配解较少的原因可能是因为算法没有搜寻到建8座及以下的可行解,也可能是算法寻优能力还不够,但是说明随着覆盖半径的缩小,需要修建更多座数量雷达站来满足约束条件;而当最大覆盖半径变为9时,可以看出最终的帕累托前沿面上对于建设6,7,8,9座雷达站均存在非支配解,最终选择的相对最优解的建站总成本为6600,实现了90.44%的面积覆盖率,需要建设8座雷达站,相比于半径为7的情况下以更小的总建站成本实现了更大的面积覆盖率,因此在实际建站过程中,部署性能更为优异的雷达可能会比多修建雷达站实现的监管效果更好,需根据具体情况进行决策。
4 结论
文章考虑到VTS雷达站在VTS系统中的关键作用,针对其选址问题进行研究,考虑到建站环境中的障碍物遮挡和雷达无线电波在介质中传播存在衰减因素,并考虑到单个雷达站失效引起水域无法被覆盖问题基于集合覆盖进行选址建模并设计粒子群算法进行多目标求解,同时对雷达最大覆盖半径展开敏感性分析,结果证明本文模型可以对VTS雷达站选址进行有效优化。但是选址是一个综合性工程,所需要顾及因素较多,因此接下来可以从其他方面进行研究,同时本文算法也有较大研究空间以期改进。
