基于分布位错法研究多条微裂纹对偏折主裂纹的影响

王强胜，张启洞，蒋哲亮，李乐毅，江晓禹

基于分布位错法研究多条微裂纹对偏折主裂纹的影响

王强胜1，张启洞2，蒋哲亮3，李乐毅1，江晓禹4*

（1.四川建筑职业技术学院，四川 德阳 618000；2.中国兵器工业试验测试研究院，陕西 华阴 714200；3.联合微电子中心有限责任公司，重庆 401332；4.西南交通大学 力学与航空航天学院，成都 610031）

采用理论方法求解多条微裂纹对偏折主裂纹的影响，重点分析偏折主裂纹尖端的力学行为及微裂纹对主裂纹扩展角度和闭合区域的影响等问题，为实际的工程应用提供理论依据。运用叠加原理将主问题分解成2个子问题，通过材料力学方法求解子问题一；基于分布位错方法求解子问题二。进一步建立关于位错密度的奇异积分方程，利用Gauss-Chebyshev数值求积分法解决位错密度方程的奇异性问题，并通过计算机编写程序，最终得到相关力学参量的数值解。得到了偏折主裂纹附近的应力场以及微裂纹长度、微裂纹个数对偏折主裂纹尖端应力强度因子的影响等相关力学参量。分析了主裂纹不同偏折角度时的闭合区域，以及微裂纹的方位角、微裂纹个数等对偏折主裂纹扩展角度的影响。裂纹面对拉应力有屏蔽作用，导致拉应力在裂纹面附近应力松弛，而裂纹尖端对拉应力有放大作用，随着应力增加将导致裂纹的扩展。一条微裂纹位于主裂纹尖端约–30°<<50°时，将使主裂纹尖端应力强度因子增加，促进主裂纹的扩展，而微裂纹位于50°<<90°或–90°<<–30°时，将使主裂纹尖端应力强度因子减小，抑制主裂纹的扩展。主裂纹尖端应力强度因子随微裂纹长度的增加而变大，随微裂纹与主裂纹间距离的增加而减小。

偏折主裂纹；微裂纹；分布位错法；应力强度因子；裂纹扩展

材料或结构中的缺陷（其最严重形式是裂纹）是不可避免的。由缺陷引起断裂所发生的机械、结构的失效，是工程中最重要、最常见、也是最危险的失效模式，对于含裂纹的材料，其裂纹尖端是最危险的区域[1]。自20世纪以来，断裂力学成为吸引大批国内外专家学者争相研究的重要领域，而对断裂力学研究的重心在裂纹尖端区域的力学行为上[2]。在脆性断裂或小范围屈服条件下，可以用裂纹尖端的应力强度因子表征裂纹尖端的应力集中现象，使含裂纹的应力集中问题得以量化解决[1]。

在外加荷载或材料内部缺陷的影响下，已有裂纹会发生扩展导致偏离原始方向，形成偏折裂纹，而偏折裂纹在工程结构中是一种非常常见的现象。随着外加载荷或材料内部缺陷的持续影响，材料中将会产生一个或多个应力集中区域，在这些区域内，会不可避免地萌生微裂纹，而微裂纹对材料的断裂行为有着非常大的影响。因此，研究微裂纹与宏观偏折主裂纹之间的相互影响有着重要的现实意义。阅读文献资料不难发现，有较多学者已做过一些裂纹之间相互影响的研究工作，如Kachanov[3]研究分析了弹性平面内含多条裂纹的应力问题。Li等[4-5]基于分布位错方法研究了无限大平面内含任意方位的微裂纹与直的主裂纹间的相互影响。Loehnert等[6]和Wang等[7]通过扩展有限元法分析了多个微裂纹对主裂纹的影响情况。Chen[8]采用权函数法研究了弹性平面内多条偏折主裂纹之间的相互作用，得到了裂纹尖端的应力强度因子。Lo[9]基于复变函数法，提出了单轴拉伸载荷作用下，无限大弹性平面内含一条偏折裂纹的理论解。Gong等[10-12]、Meguid等[13]和Hori等[14]利用复变函数法研究了多条裂纹之间的相互作用。Mukai[15]研究了含偏折裂纹的半平面在刚性圆柱压头作用下的应力问题。王强胜等[16-17]通过分布位错方法研究了复杂载荷作用下，半无限大弹性平面内含一条直的主裂纹的力学行为。He等[18-19]分析了界面偏折裂纹问题。

上述研究只考虑了直的宏观裂纹与微裂纹间的相互影响，并没有分析多条微裂纹对偏折宏观主裂纹的影响情况。因此，本文通过分布位错方法，重点研究了无限大弹性平面内包含多条任意位置的微裂纹与一条偏折主裂纹之间的相互影响问题。得到了偏折主裂纹附近的应力场、裂纹尖端的应力强度因子以及主裂纹的扩展角度等相关力学参量，得到的结果将为实际的工程应用提供理论依据。

1 理论模型

在实际裂纹扩展中，主裂纹的扩展路径往往是弯曲的，基于这样的考虑，本文重点分析微裂纹对偏折主裂纹的影响。在无限大平面内有一条偏折的主裂纹和条（≥3）任意位置的微裂纹，外加载荷是远场的均匀拉伸与剪切的复杂载荷，分别用∞和∞表示，理论模型如图1所示。偏折主裂纹由2段倾斜段组成，分别标记为裂纹“1”和裂纹“2”，长度分别为2和2，倾斜角度分别为和，在本文称之为裂纹角度；-2条微裂纹分别标记为“3”“4”……“”，微裂纹的长度均为2，微裂纹中心与整体坐标原点的距离均为，微裂纹的倾斜角度分别为3、4……α，微裂纹相对于整体坐标原点的位置分别用3、4……θ表示，称之为微裂纹方位角，定义、、α和θ逆时针方向为正。为方便求解，用位错列代替裂纹时，裂纹编号也是相应位错列的编号。接下来，采用分布位错方法对这一问题进行理论求解。

2 理论求解

2.1 叠加原理

分布位错方法求解裂纹问题的核心思想是通过连续分布的位错来等效代替裂纹产生的应力和变形，从Bueckner定理出发，将图1所研究的问题分解成2个子问题，其中子问题一：无裂纹和位错时，远场复杂载荷作用下平面内产生的应力问题。该问题的应力场可以表示为：

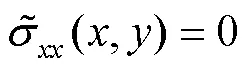
子问题二：无外加载荷作用时，平面内含有四列连续分布的刃型位错产生的应力问题[20]，基于分布位错技术求解子问题二。最后将这2个子问题通过叠加原理得到图1所示问题的完整解。

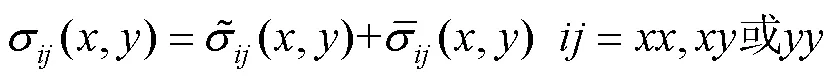
2.2 关于位错密度积分方程的建立

在无限大平面内，位于整体坐标系（，0）处的一个刃型位错产生的应力场可以通过文献[20]得到：

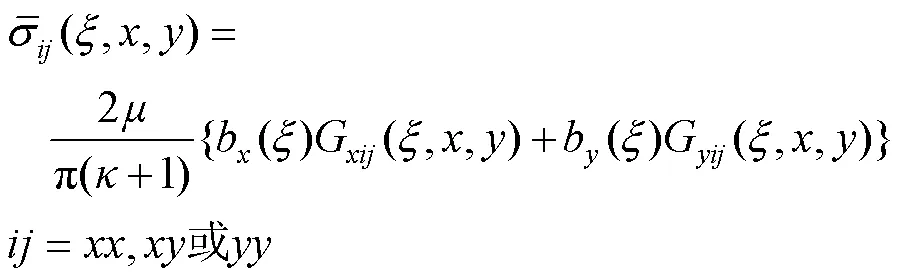
式中：μ是剪切模量；κ是Kolosov常数，平面应力状态下κ=(3–ν)/(1+ν)，平面应变状态下κ=3–4ν；ν是泊松比；bx和by是刃型位错Burgers矢量；G*是位错密度影响函数，可通过文献[20]得到。

类似地，可以得到在裂纹1、2、3和4区域的总位错引起的应力分量，如下：

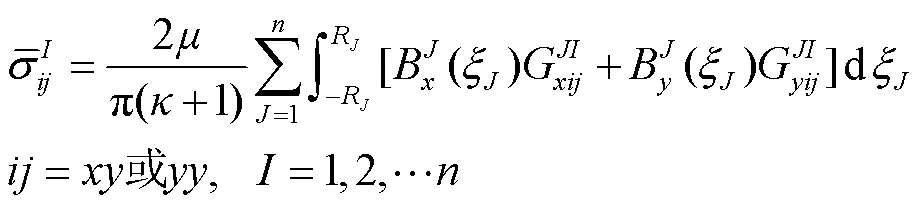
式中，1=；2=；3=4=……R=；(ξ)是位错密度函数；无限大弹性平面内含有2个任意方向裂纹的影响函数，已通过文献[4,20]得到，式（4）中的影响函数可以通过替换裂纹位置和角度得到。

图1所示问题的边界条件必须满足裂纹面无牵引力，即将式（4）代入式（2），得到关于位错密度的积分方程，如下：

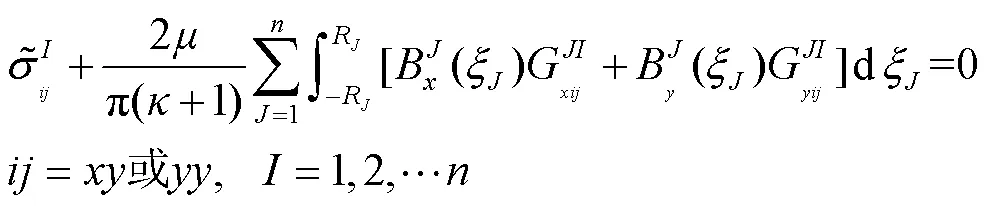
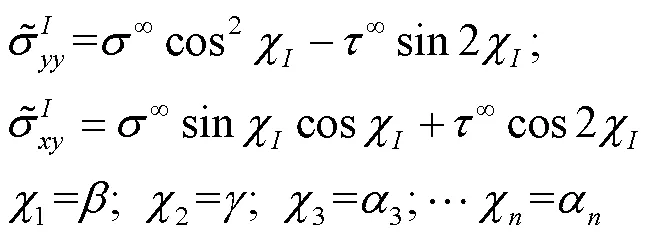
至此，关于位错密度的积分方程已经建立，式（5）中共有2个代数方程组，有2个待求解的位错密度函数，方程数等于未知数个数，理论上是可以求解的，但该方程是奇异的，其解析解很难得到。因此，本文采用一种有效的数值求解方法Gauss-Chebyshev求积分法进行数值求解[21-22]。

2.3 积分方程的数值求解

Gauss-Chebyshev求积分法，首先需将式（5）中的积分区间[–R，R]通过式（7）归一化到区间[–1, 1]上。

此时，式（5）变为：

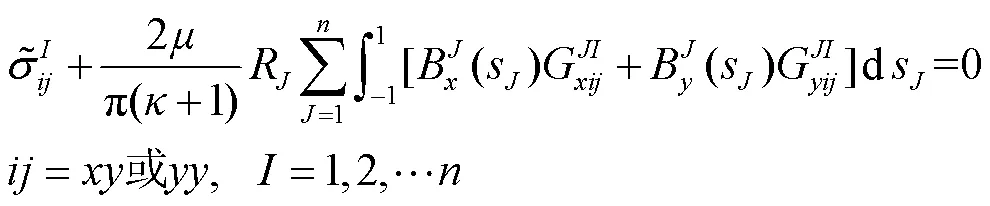
由于裂纹两端是奇异的，位错密度也是如此，从文献[20]中得到位错密度函数的表达式，如下：

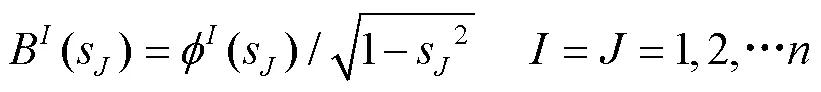
利用Gauss-Chebyshev求积分方法，可以将式（8）中的每个方程离散为-1个代数方程，如下：

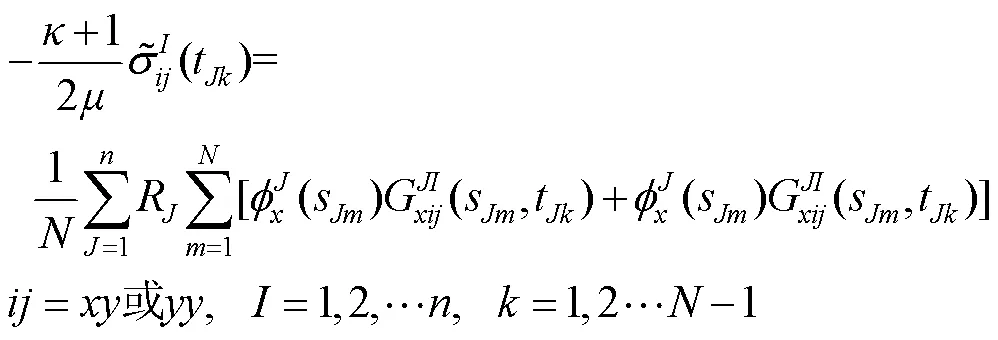
式中，为离散积分点的个数，越大结果越精确。在式（10）中，共有2×个未知数，但只得到2×(–1)个代数方程。由于裂纹的2个尖端处位移为零，所以每个裂纹上，位错总的Burgers矢量必须等于零，以保证裂纹上无净位错，通过这个条件得到2–2个补充方程：

在裂纹偏折处的位错密度值应相等，再次得到2个补充方程：

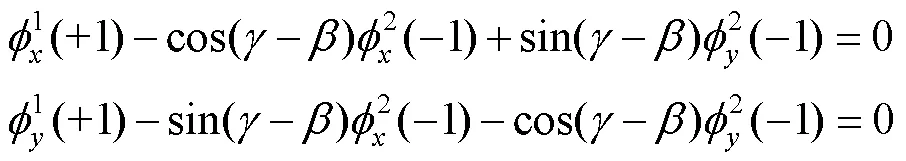
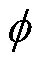
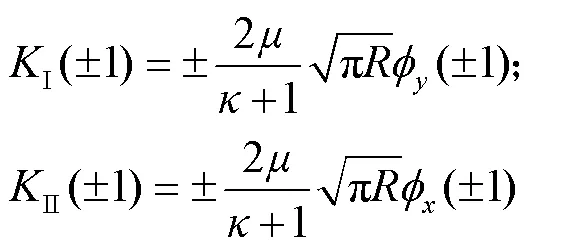
同时，也可以得到整体坐标系--下的应力场：

3 理论解的验证

为保证图1理论模型计算的正确性，同时能够与已有文献[20]的结果对比，故在本节理论解的验证模型中暂不考虑微裂纹的影响，只施加远场的均匀拉伸载荷∞，其他相关参数取=2、0°、=1.0、∞= 0、=30，本文计算结果（散点表示）与文献[20]结果（实线表示）对比如图2所示。

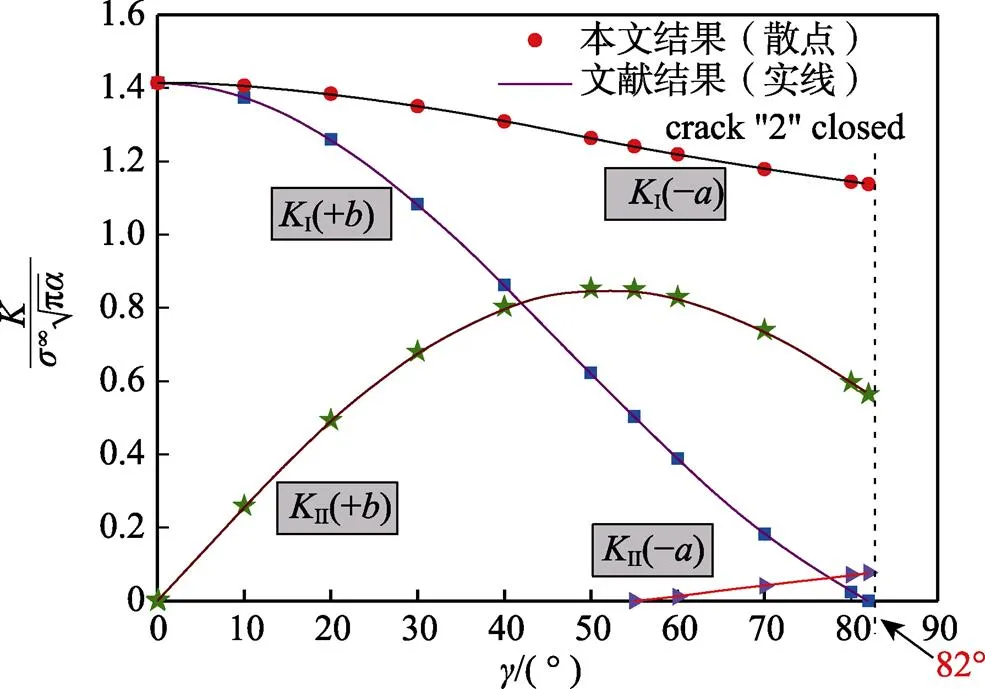
图2 本文结果与文献结果对比

从图2的结果对比中可以看到，不管是变化趋势还是数值大小，本文的计算结果与文献[20]中的结果都是比较吻合的，说明本文采用的分布位错计算方法与数值计算程序得到的结果是可靠的。因此，本文以下结果均采用分布位错方法，并通过Wolfram Mathematical 9.0编程得到其数值解。

4 结果分析

4.1 裂纹附近应力场

对于含裂纹的材料，其裂纹尖端是应力最集中，也是最危险的区域。裂纹附近应力场的分析与计算结果有助于研究裂纹之间的相互作用。因此，为了更加直观地看到偏折主裂纹附近的应力分布情况，通过式（15）得到了偏折主裂纹附近的应力场，如图3为不考虑微裂纹与偏折主裂纹之间的相互作用时偏折主裂纹附近归一化应力场的等高线图，相关参数取=2、30°、=0°、=1.0、∞=0、=30。

图3a为偏折主裂纹附近归一化的拉伸应力场等高线图，可以看到：裂纹面顶部和底部区域的拉应力σ小于外加拉伸载荷∞，而裂纹两端点区域的拉应力σ大于∞，说明裂纹面对拉应力有屏蔽作用，导致拉应力在裂纹面附近的区域应力松弛，而裂纹尖端区域对拉应力有放大作用。因此，在裂纹尖端附近发生应力集中，随着应力增加将导致裂纹扩展。图3b为偏折主裂纹附近归一化的切应力场等高线图，可以看到，处于第一象限和第三象限的切应力主要以负值为主，而处在第二象限和第四象限的切应力主要以正值为主。

4.2 倾斜角β对裂纹“2”闭合区域的影响

在上一节结果验证中，当相关参数取=2、0°、=1.0、∞=0、=30，裂纹“2”的倾斜角度=82°时，裂纹“2”将发生闭合。因此，有必要研究偏折裂纹中，裂纹“1”的倾斜角对裂纹“2”何时发生闭合的影响情况，这将有助于对存在缺陷（裂纹）材料的破坏形式有更好的说明。相关参数取=2、=1.0、∞=0、=30，结果如图4所示。

若裂纹“1”的倾斜角=0°时，裂纹“2”在区间[82.0°, 118.3°]或[–118.3°, –82°]时将发生闭合，该闭合区间关于轴对称分布。当裂纹“1”的倾斜角=15°时，裂纹“2”在区间[85.5°,111.6°]或[–121.4°, –78.7°]时将发生闭合，该闭合区间与=0°时的闭合区间有较大的变化，并非对称分布，而是在越靠近裂纹“1”的区域，造成裂纹“2”发生闭合的区域越大，在闭合区间内容易造成材料的剪切破坏。

4.3 微裂纹对偏折主裂纹的影响

4.3.1 微裂纹长度对偏折主裂纹尖端应力强度因子的影响

在单轴拉伸载荷σ作用下，微裂纹长度对偏折主裂纹尖端应力强度因子的影响情况如图5所示，其他相关参数取=4、30°、=15°、3=30°、4=–30°、3=4=0°、=1.0、∞=0、=30。

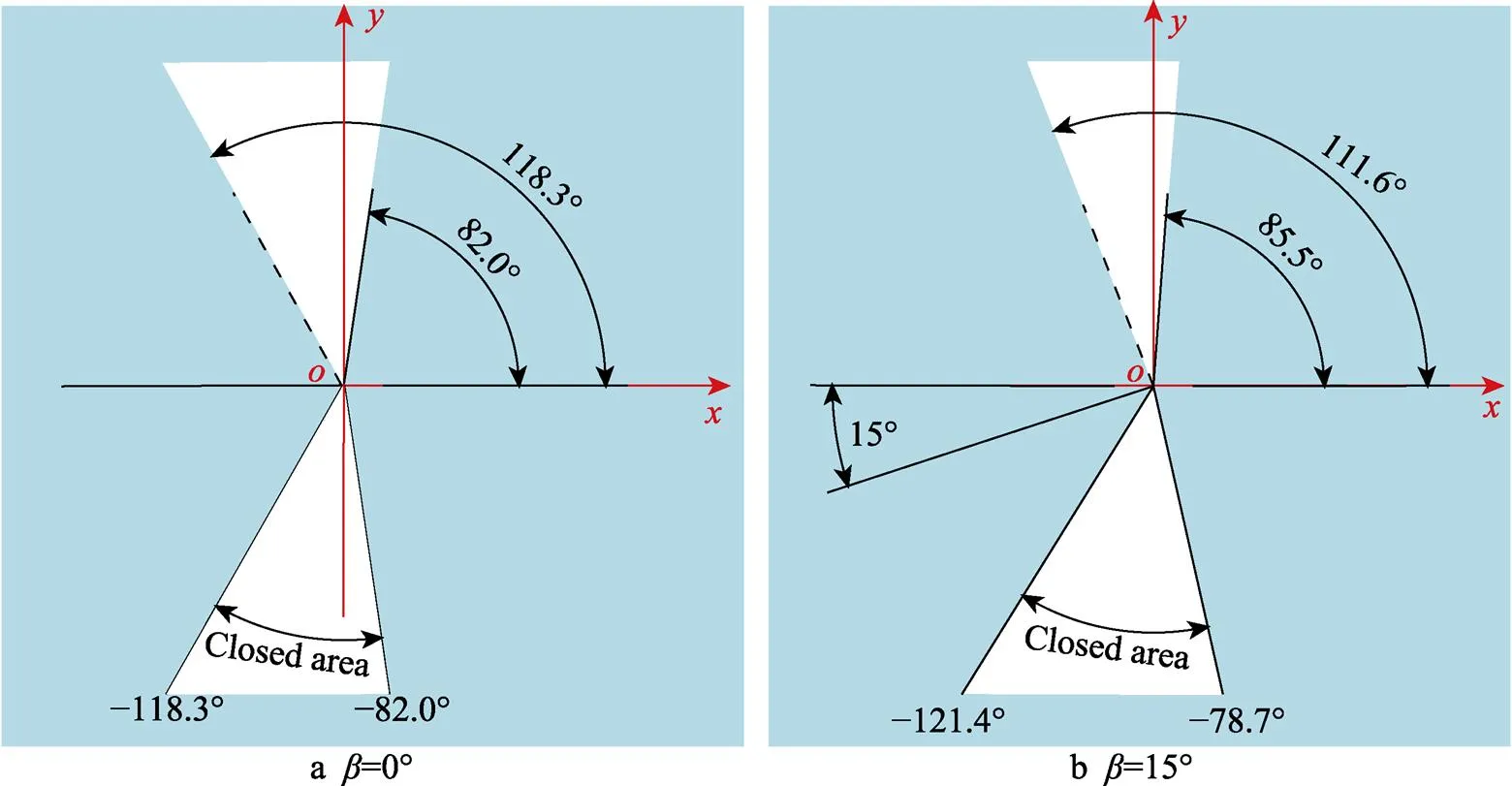
图4 裂纹“1”倾斜角β对裂纹“2”的影响

图5 应力强度因子随微裂纹长度的变化曲线

从图5的数据结果中看到，偏折主裂纹尖端的应力强度因子I或II都随着微裂纹长度的增加而变大，随着微裂纹与偏折主裂纹间距离/的增加，微裂纹对主裂纹尖端应力强度因子的影响就会减弱，是因为随着距离/的增加以及微裂纹长度/的减小，微裂纹对偏折主裂纹附近应力场的影响将会减弱。

4.3.2 微裂纹方位对偏折主裂纹尖端应力强度因子的影响

在单轴拉伸载荷σ作用下，微裂纹方位角对偏折主裂纹尖端应力强度因子的影响如图6所示，其他相关参数取=4、30°、=15°、4=0°、3=4=0°、=1.0、=0.5、4=0.5、∞=0、=30。

图6 应力强度因子随微裂纹方位角θ的变化曲线

从图6a中看到，当只有一条微裂纹时，微裂纹方位角在–30°<<50°范围时，微裂纹对主裂纹尖端I有放大作用，而在–90°<<−30°和50°<<90°范围时对I有屏蔽作用。由4.1节拉应力场可知，裂纹面对拉应力有屏蔽作用，而裂纹尖端区域对拉应力有放大作用。因此，微裂纹位于偏折主裂纹尖端前方–30°<<50°时，微裂纹将使偏折主裂纹尖端应力强度因子增加，促进主裂纹的扩展，而微裂纹位于主裂纹面顶部50°<<90°或底部–90°<<–30°时，微裂纹将使偏折主裂纹尖端应力强度因子减小，抑制了主裂纹的扩展。随着微裂纹个数的增加，其对主裂纹尖端I的影响趋势同一条微裂纹，但影响程度更大。从图6b中看到，当只有一条微裂纹时，微裂纹方位角在−64°<<30°或85°<<90°范围时，微裂纹对主裂纹II有放大作用，而在–90°<<–64°或30°<<85°范围时对II有屏蔽作用，当微裂纹位于0°左右时，对II的屏蔽作用几乎可以忽略。由4.1节切应力场分析结果可知，正向切应力将会使主裂纹尖端应力强度因子II变大，而负向切应力将会使II减小。因此，微裂纹位于–64°<<30°或85°<<90°范围时导致II增加，加快主裂纹滑移面的剪切破坏，而位于–90°<<-64°或30°<<85°范围时导致II减小，抑制滑移面的剪切破坏。从图6b中看到，微裂纹个数对主裂纹尖端II的影响较小。

4.3.3 微裂纹对偏折主裂纹扩展方向的影响

最大周向应力准则认为含裂纹的材料会向裂纹尖端周向拉应力最大的方向发生扩展，可以有效判断材料的断裂方向[23]。因此，本文运用最大周向应力准则研究偏折主裂纹的扩展方向，用偏折主裂纹尖端的应力强度因子计算裂纹的扩展方向，如下：

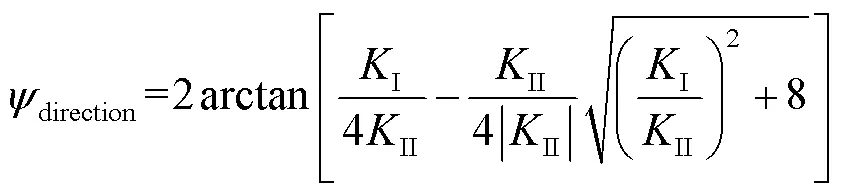
式中，定义逆时针方向为正，即direction>0时，裂纹在坐标系一、二象限区域内发生扩展；direction<0时，裂纹在坐标系三、四象限区域内发生扩展。

在单轴拉伸作用下，主裂纹扩展角度随微裂纹长度或微裂纹方位角的变化情况如图7所示，其他相关参数取=4、30°、=15°、4=0°、3=4=0°、=1.0、=0.5、4=0.5、∞=0、=30。

从图7a微裂纹长度对主裂纹扩展角度的影响中看到，当无微裂纹影响时，主裂纹随着外加载荷的增加，将在第四象限内以–12.94°的方向发生扩展，因为由图3应力场的分析可知，不管是正应力，还是切应力，都是在第四象限区域内最大。而当有一条微裂纹处于主裂纹尖端的右上方时，由于主裂纹位于微裂纹应力场的第三象限，该象限内是拉引力场和负向的切应力场的叠加，将会吸引主裂纹朝着微裂纹所在的方向发生扩展，即主裂纹随着微裂纹长度的增加，在第四象限内逐渐朝着轴的方向发生扩展。当有2条对称于轴分布的微裂纹时，主裂纹随微裂纹长度的增加，其扩展方向与一条时恰好相反，且扩展角度的增速更大，这表明该模型下，微裂纹处于主裂纹的右下方时，更容易造成裂纹扩展。从图7b中看到，微裂纹方位角对主裂纹扩展角度的影响较小，在–90°<90°范围内变化过程中，=60°时，微裂纹对主裂纹扩展角度的影响最大，=23°时，其影响相对较小。

4.4 微裂纹个数对偏折主裂纹的影响

在单轴拉伸作用下，微裂纹个数对偏折主裂纹尖端应力强度因子及扩展角度的影响如图8所示，其他相关参数取=2…9、30°、=15°、3=45°、4=30°、5=15°、6=0°、7=–15°、8=-30°、9=–45°、=0°、=1.0、=0.5、=7.5、∞=0、=30。

从图8a中看到，随着微裂纹个数的增加，偏折主裂纹尖端一型应力强度因子I将不断增加，但其增幅相对缓慢，而II受微裂纹个数的影响相对较小。同图7a中所得到的结论一致，微裂纹位于主裂纹右下方时，更容易引起主裂纹的扩展，而位于右上方时，扩展相对较难。从图8b中看到，在该模型的裂纹方位下，微裂纹位于主裂纹右上方时，主裂纹在第四象限内逐渐朝着轴的方向发生扩展，而微裂纹位置越往主裂纹的右下方时，主裂纹将在第四象限内逐渐向远离轴的方向发生扩展，该结论同图7a中所得到的结论一致，其原因已在前文说明，此处不再赘述。

图7 偏折主裂纹扩展角度的变化曲线

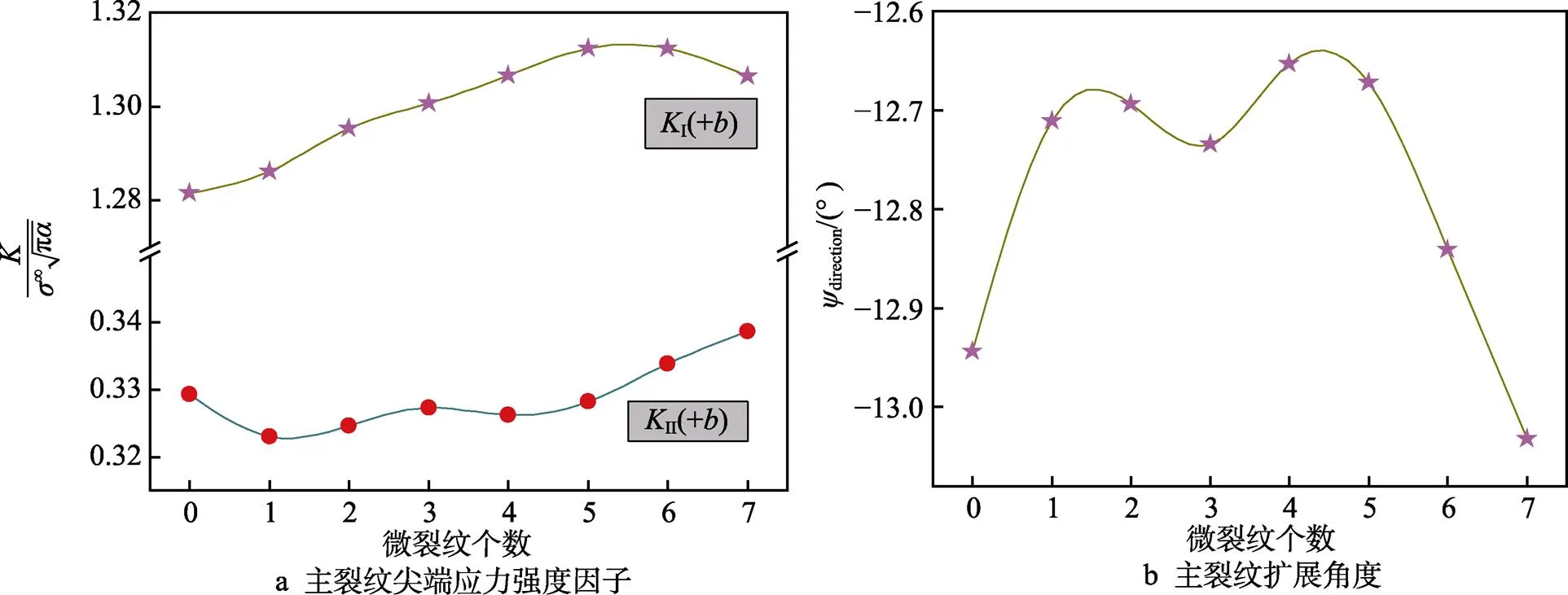
图8 微裂纹个数对主裂纹的影响

4.5 实验观察

本节中，用已有文献的实验观察结果说明本研究的重要性，如图9所示为扫描电镜实验观察结果。实验材料为U71mn钢，试样为矩形板（120 mm×15 mm× 1 mm），裂纹位于试样中间，试样承受对称三点弯曲的疲劳载荷。

从扫描电镜观察结果可以看到：主裂纹将发生分支和偏折现象，如图9a所示用红色圆圈标识，而在主裂纹扩展路径附近存在微裂纹，如图9b所示用红色箭头标识。在宏观断裂力学分析中，材料中很难避免孔洞、微裂纹、夹杂物等，同时，随着宏观主裂纹的扩展，也会不断萌生微裂纹，这些缺陷将对主裂纹的扩展产生较大影响。基于此实验，本文选取材料中非常常见的裂纹偏折和微裂纹作为理论研究对象，以分析微裂纹对宏观偏折主裂纹的影响情况，从而为实际的工程应用提供理论依据。

图9 实验观察结果[2,24]

5 结论

本文通过分布位错方法得到了无限大弹性平面内含多条微裂纹与一条偏折主裂纹的理论解，分析了微裂纹对偏折主裂纹的影响情况，得到以下结论：

1）裂纹面对拉应力有屏蔽作用，导致拉应力在裂纹面附近区域应力松弛，裂纹尖端对拉应力有放大作用，即在裂纹尖端发生应力集中，随着应力增加将导致裂纹扩展。

2）一条微裂纹位于主裂纹尖端–30°<<50°时，将使主裂纹尖端应力强度因子增加，促进主裂纹的扩展，而微裂纹位于50°<<90°或–90°<<–30°时，将使主裂纹尖端应力强度因子减小，抑制主裂纹的扩展。

3）主裂纹尖端应力强度因子随微裂纹长度的增加而变大，随微裂纹与主裂纹间距离/的增加而减小。

4）当无微裂纹影响时，主裂纹随外加载荷的增加，将在第四象限内以–12.94°的方向发生扩展；当有一条微裂纹处于主裂纹尖端右上方时，将会吸引主裂纹朝着微裂纹所在的方向发生扩展；当有2条对称于轴分布的微裂纹时，主裂纹随微裂纹长度的增加，其扩展方向与一条时恰好相反，且扩展角度增速更大。

5）主裂纹尖端I随微裂纹个数的增加而不断变大，但微裂纹个数对II的影响相对较小。

[1] 范天佑. 断裂理论基础[M]. 北京: 科学出版社, 2003: 11-14. FAN Tian-you. Theoretical Basis of Fracture[M]. Beijing: Science Press, 2003: 11-14.

[2] LI Xiao-tao, YANG Hong-da, ZAN Xiao-dong, et al. Effect of a Micro-Crack on the Kinked Macro-Crack[J]. Theoretical and Applied Fracture Mechanics, 2018, 96: 468-475.

[3] KACHANOV M. A Simple Technique of Stress Analysis in Elastic Solids with many Cracks[J]. International Journal of Fracture, 1985, 28(1): R11-R19.

[4] LI Xiao-tao, LI Xu, JIANG Xiao-yu. Influence of a Micro-Crack on the Finite Macro-Crack[J]. Engineering Fracture Mechanics, 2017, 177: 95-103.

[5] LI Xiao-tao, LI Xu, YANG Hong-da, et al. Effect of Micro-Cracks on Plastic Zone Ahead of the Macro-Crack Tip[J]. Journal of Materials Science, 2017, 52(23): 13490- 13503.

[6] LOEHNERT S, BELYTSCHKO T. Crack Shielding and Amplification Due to Multiple Microcracks Interacting with a Macrocrack[J]. International Journal of Fracture, 2007, 145(1): 1-8.

[7] WANG Heng, LIU Zhan-li, XU Dan-dan, et al. Extended Finite Element Method Analysis for Shielding and Amplification Effect of a Main Crack Interacted with a Group of nearby Parallel Microcracks[J]. International Journal of Damage Mechanics, 2016, 25(1): 4-25.

[8] CHEN Y Z. Stress Intensity Factors for Curved and Kinked Cracks in Plane Extension[J]. Theoretical and Applied Fracture Mechanics, 1999, 31(3): 223-232.

[9] LO K K. Analysis of Branched Cracks[J]. Journal of Applied Mechanics, 1978, 45(4): 797-802.

[10] GONG San-xia, HORII H. General Solution to the Problem of Microcracks near the Tip of a Main Crack[J]. Journal of the Mechanics and Physics of Solids, 1989, 37(1): 27-46.

[11] GONG S X, MEGUID S A. Microdefect Interacting with a Main Crack[J]. International Journal of Mechanical Sciences, 1992, 34(12): 933-945.

[12] GONG S X. On the Main Crack-Microcrack Interaction under Mode III Loading[J]. Engineering Fracture Me­chanics, 1995, 51(5): 753-762.

[13] MEGUID S A, GAULTIER P E, GONG S X. A Com­parison between Analytical and Finite Element Analysis of Main Crack-Microcrack Interaction[J]. Engineering Fracture Mechanics, 1991, 38(6): 451-465.

[14] HORI M, NEMAT-NASSER S. Interacting Micro-Cracks near the Tip in the Process Zone of a Macro-Crack[J]. Journal of the Mechanics and Physics of Solids, 1987, 35(5): 601-629.

[15] MUKAI D J. An Analysis of a Near-Surface Crack Bran­ching under a Rigid Indenter[J]. Journal of Tribology, 2000, 122(1): 23-29.

[16] 王强胜, 李孝滔, 昝晓东, 等. 分布位错法研究钢轨表面边缘直裂纹的力学行为[J]. 表面技术, 2020, 49(2): 200-211. WANG Qiang-sheng, LI Xiao-tao, ZAN Xiao-dong, et al. Mechanical Behavior of Straight Crack on the Edge of Rail Surface by Distributed Dislocation Method[J]. Surface Technology, 2020, 49(2): 200-211.

[17] 王强胜, 李孝滔, 昝晓东, 等. 分布位错法研究移动赫兹压力作用下次表面裂纹的力学行为[J]. 表面技术, 2019, 48(6): 252-260. WANG Qiang-sheng, LI Xiao-tao, ZAN Xiao-dong, et al. Mechanical Behaviors of Subsurface Crack under Moving Hertz Pressure by Distributed Dislocation Method[J]. Surface Technology, 2019, 48(6): 252-260.

[18] HE Ming-yuan, BARTLETT A, EVANS A G, et al. Kinking of a Crack out of an Interface: Role of In-Plane Stress[J]. Journal of the American Ceramic Society, 1991, 74(4): 767-771.

[19] HE Ming-yuan, HUTCHINSON J W. Kinking of a Crack out of an Interface[J]. Journal of Applied Mechanics, 1989, 56(2): 270-278.

[20] HILLS D A. Solution of crack problems: the distributed disclocation technique[M]. Dordrecht: Kluwer Academic Publishers, 1996.

[21] ERDOGAN F, GUPTA G D, COOK T S. Numerical Solution of Singular Integral Equations[M]//Methods of Analysis and Solutions of Crack Problems. Springer, Dordrecht, 1973: 368-425.

[22] ERDOGAN F, GUPTA G D, COOK T S. Numerical Solution of Singular Integral Equations[M]//Sih GC. Methods of analysis and solutions of crack problems. Dordrecht: Springer, 1973: 368-425.

[23] KAYA A C, ERDOGAN F. On the Solution of Integral Equations with Strongly Singular Kernels[J]. Quarterly of Applied Mathematics, 1987, 45(1): 105-122.

[24] ERDOGAN F, SIH G C. On the Crack Extension in Plates under Plane Loading and Transverse Shear[J]. Journal of Basic Engineering, 1963, 85(4): 519-525.

[25] LI Xiao-tao, SHEINERMAN A G, YANG Hao, et al. Theoretical Modeling of Toughening Mechanisms in the CrMnFeCoNi High-Entropy Alloy at Room Temperature [J]. International Journal of Plasticity, 2022, 154: 103304.

Effect of Multiple Micro-cracks on Kinked Macro-cracks Based on the Distributed Dislocation Method

1,2,3,1,4*

(1. Sichuan College of Architectural Technology, Sichuan Deyang 618000, China; 2. Test and Measuring Academy of Norinco Group, Shaanxi Huayin 714200, China; 3. United Microelectronics Center, Chongqing 401332, China; 4. School of Mechanics and Aerospace Engineering, Southwest Jiaotong University, Chengdu 610031, China)

The work aims to study the problem of the effect of multiple micro-cracks on the kinked macro-crack by a theoretical method. In this paper, the mechanical behavior of the kinked macro-crack tip and the effect of multiple micro-cracks on the kinked macro-crack propagation angle and the closed regions of the kinked macro-crack were analyzed mainly. The obtained results will provide a theoretical basis for practical engineering applications. When solving the problem studied in this paper through theoretical analysis, it was divided into two steps. Firstly, the problem considered in this paper was divided into two sub-problems based on the superposition principle, and then solved one by one. Secondly, the first sub-problem was solved by material mechanics and the second sub-problem was solved by the distributed dislocation technique. Further, a singular integral equation about the dislocation density function was established. The singularity problem of the dislocation density equation was solved based on the Gauss-Chebyshev integration method and the numerical solution of the equation was obtained by means of computer programming. Finally, a series of valuable mechanical parameters about the kinked macro-crack were obtained. In this paper, some results were obtained which will provide a theoretical basis for practical engineering applications. For example, the stress field near the kinked macro-crack and the related mechanical parameters of the macro-crack tip were obtained. Specifically, these mechanical parameters affected the micro-crack length and the number of micro-cracks on the stress intensity factor at the tip of the macro-crack. The closed regions of the macro-crack with different kinked angles, and the effect of the orientation of micro-cracks and the number of micro-cracks on the propagation angle of the kinked macro-crack were analyzed. Several practical conclusions were obtained in this paper. It is concluded that the regions near the kinked macro-crack surface has a shielding effect on the tensile stress, which will lead to stress relaxation of the tensile stress near the crack surface. The regions near the crack tip will amplify the tensile stress. In other words, the stress will be concentrated near the crack tip, and the kinked macro-crack tip will further propagate as the increased of the applied load. When only one micro-crack is located at the macro-crack tip about –30°<<50°, the stress intensity factor at the kinked macro-crack tip will increase, which will promote the propagation of the macro-crack. When the micro-crack is located at 50°<<90° or –90°<<–30°, the stress intensity factor at the tip of the macro-crack will decrease, which will inhibit the propagation of the macro-crack. The stress intensity factor at the tip of the macro-crack will become larger with the increase of the micro-crack length, and decrease with the increase of the distance between the micro-crack and the macro-crack.

kinked macro-crack; micro-crack; distribution dislocation; stress intensity factor; crack propagation

2022-08-03；

2023-02-17

TG174

A

1001-3660(2023)10-0439-09

10.16490/j.cnki.issn.1001-3660.2023.10.040

2022-08-03；

2023-02-17

国家自然科学基金资助项目（11472230）

Supported by the National Natural Science Foundation of China (11472230)

王强胜, 张启洞, 蒋哲亮, 等.基于分布位错法研究多条微裂纹对偏折主裂纹的影响[J]. 表面技术, 2023, 52(10): 439-447.

WANG Qiang-sheng, ZHANG Qi-dong, JIANG Zhe-liang, et al. Effect of Multiple Micro-cracks on Kinked Macro-cracks Based on the Distributed Dislocation Method[J]. Surface Technology, 2023, 52(10): 439-447.

通信作者（Corresponding author）

责任编辑：马梦遥