基于二重抽样的权数调整研究

王小宁

（中国传媒大学 数据科学与智能媒体学院，北京 100024）

0 引言

在实际抽样调查中，分层抽样以其效率高、费用少、精度高、方法灵活的优点而被广泛采用，已成为近代统计调查方法中最常用的方法之一。李林蔓（2015）[1]认为对于分层抽样的传统研究一般集中在样本选择的方法和置信区间的设定上，并总结了比例分层抽样和非比例分层抽样这两种抽样方法的适用情况和优缺点。正是由于分层抽样的这种重要性地位，因此研究在不同情况下分层抽样中样本量的确定和分配问题就变得特别重要[2—5]。而现有关于分层抽样或关于样本量的确定和分配的理论方法的适用环境发生了转变，因此样本量的确定和分配方法也应该做到具体问题具体分析。

首先，根据分层的目的来确定各分层的标志，即根据研究的需要来进行分层，当分层是为了提高抽样效率时，就会出现以哪些指标作为分层标志，这个时候就需要视具体情况来决定是按照主要指标来分层，还是按照照顾多数指标的折衷方案来分层。

其次，分层抽样需要事先掌握与总体单元有关的各种信息，如分层的抽样框、分层后各层的总体单元数与实际总体的关系、预设费用等。但在某些情况下，可能没有关于层的抽样框，这个时候可以先采用预抽样，再根据样本单元进行分层，这种分层方法称作事后分层。

最后，还需要确定分层的界限以及个数。如果此时用于分层的指标是属性变量，例如性别、行政区域等，那么通常可以按照各个分类值直接进行分层。但还需根据调研目的来明确分层的大小，例如在全国性的抽样调查中，若按地区分层，既可以按照行政区域的省、市分层，又可以将经济发展情况类似的省、市合并在一起作为一个层。

在调查过程中出现权数调整的情况一般可分为两类：结构调整和规模调整。结构调整的目的是实现样本与总体结构的一致性，常见的方法有迭代、校准、广义回归等；而规模调整的目的是实现样本与总体规模的一致性，其中常见的场景之一是处理样本无回答部分。在以随机缺失为前提的权数调整研究中，利用辅助信息调整权重的校准加权方法自1992 年提出以来就广受关注，已发展为适用于二阶抽样、二重抽样等不同情形。

整体上看，基于二重抽样的权数调整在理论研究上较为丰富，但在国内的实际应用和相关的调查方案设计上仍较少。据此，本文基于《A 省环境群众满意度测评抽样设计调查》（以下称《A 省满意度调查》），探讨在实际中如何根据初始限制条件来构建抽样框，进行分层抽样样本量的确定和分配，以及如何基于二重抽样处理无回答部分，并采用迭代法和事后分层相结合的方法调整权数。同时，结合刀切法计算采用二重抽样和不采用二重抽样情况下估计的标准差，证明基于二重抽样权数调整方法的实用性和有效性。

1 相关理论

在实际抽样调查中，尤其是在面对一些复杂的、人际性的社会问题研究时，电话调查、面访等在当下仍是不可或缺的调查方式。针对无人接听、拒访、拒接、手机关机和访问中断五类无回答情况，本文采用二重抽样的方法进行补救。

二重抽样是指在抽样时分两步抽取样本，即先从总体中抽取一个较大的样本，称为第一重样本，对其进行调查以获得总体的某些辅助信息，为下一步的抽样估计提供条件，然后再进行第二重抽样。第二重抽样调查是主调查，通常情况下第二重样本是从第一重样本中抽取的，即为第一重样本的子样本，但有时也可以从总体中独立抽取。由于样本是分两次抽取的，因此该抽样过程被称为二重抽样。

记S(1)为第一重样本，被选中的样本单元用下列随机变量来表示：

记S(2)为第二重样本，被选中的样本单元用下列随机变量表示：

第二重样本单元被抽中的概率依赖于其是否在第一重样本中，也可能依赖于在第二重样本中收集到的辅助信息，这种依赖性用P(Di=1|Z)表示，Z表示向量(Z1,Z2,…,ZN)，假设第一重样本信息已知，则可以得到满足Z的条件期望，进而得到第二重样本权重为：

由于《A 省满意度调查》不仅想要得到全省关于环境满意度的整体情况，还希望得到所有地级市（自治州）环境满意度的情况，因此以地级市（自治州）为子总体进行设计，以保证每个地级市（自治州）内都有样本分布，样本量根据各地级市（自治州）的人口规模进行相应调整。

以电话调查为例，二重抽样处理无回答部分的具体方法如下：首先，在CATI系统中记录无人接听、拒访、拒接、手机关机和访问中断的受访者号码；其次，在上述样本中抽取子样本重新进行调查，由于这部分人群调查难度较高，因此在给定经费的条件下可采取奖励措施提高回答率；最后，将首次调查成功的样本和二重抽样的样本合并进行分析。

由于《A 省满意度调查》的抽样设计采用两阶段分层随机尾号法配合二重抽样，且电话调查中包括固定电话和移动电话，因此抽样中涉及三个抽样框，分别是固定电话抽样框、移动电话抽样框以及二重抽样抽样框。

2 样本量的确定与权数调整过程

抽样设计中，样本量n的确定与抽样误差、调查成本及所需估计的统计量有关。如何合理确定调查中各地级市（自治州）所需的目标样本量，并以较高的精度对总体的满意度做出估计是本次抽样设计的核心需求。

2.1 地级市样本量确定

在简单随机抽样情况下，各地级市（自治州）所需基础样本量n0和绝对误差限度d存在一定的关系。设在置信度1-α下，样本均值的绝对误差限为d，则有P(|-|≤d)=1-α。用S2表示该地级市（自治州）的总体方差，则各地级市（自治州）在简单随机抽样时目标样本量应为：

在统计意义上，当总体规模N达到100 万以上时，N的变化对n0不再具有明显影响，根据以往满意度调查数据，在百分制问卷中，满意度调查的总体方差约为0.3。由此，可计算得到以地级市（自治州）为总体的基础样本量n0与绝对误差d的变化关系图，如图1所示。

图1 绝对误差d与各地级市（自治州）基础样本量n0变化图

从图1 可以看出，在简单随机抽样情况下，绝对误差从4%减小到3%，基础样本量增加559；而当绝对误差从3%减小到2%时，基础样本量增加1595。不断增加基础样本量，虽然能减小误差值，但是变化越来越缓慢。若能保证基础样本量n0=1279，则绝对误差可降低到3%，在此之前曲线的变化相对陡峭，在此之后曲线的变化相对平缓，此时的抽样效果较好，抽样成本也较低。

假定抽样方法确定设计效应deff=1.1。调整后各地级市（自治州）样本量n1=n0×deff，计算可得n1=1407。本着方案实施的便利性原则，可取调整后各地级市（自治州）的样本量为1400。如果省内各地级市（自治州）人口规模相差较大，应对人口规模大的地级市（自治州）适当增加样本量。

基于此，可将A 省各地级市（自治州）划分为三大类：人口规模在500 万及以上的为第一类，300 万至500 万人口的为第二类，人口规模小于300 万的为第三类。

取三类地级市（自治州）的人口规模均值，分别约为900 万、400 万、200 万，测定标准取自然对数，经计算三个类别的结果之比约为1.28:1.14:1。以此作为各类别地级市（自治州）样本量的调整系数，得到样本量分别为1800、1600、1400。为了比较不同地级市（自治州）区（县）层级上的满意度差异，一方面要求样本在地级市（自治州）内有所分布，另一方面要求在每个区（县）内都有样本遵循如下原则：

（1）地级市内所有区（县）全覆盖。

（2）人口规模大的区（县）多分，人口规模小的区（县）少分。

若直接对各区（县）按人口规模比例分配样本，则会导致部分区（县）之间样本量差距过大，一些区（县）可能因分得的样本量过少而使样本失去对区（县）的代表性。考虑到区（县）间人口规模差异程度较地级市（自治州）间差异程度小，为使样本量的分配更加合理，采用国际上的惯用方法，对各区（县）的人口规模做平方根运算，按该比例来分配样本量。以B市为例，采用人口规模比例分配法和人口规模平方根分配法的结果如表1所示，可见按人口规模平方根分配可有效缩小各区（县）间样本量的差距。

表1 B市各区（县）样本量分配结果比较

从表1 可以看出，由于第1 个区（县）人口规模是第8个区（县）人口规模的5.1 倍，采用人口规模平方根分配法，第1个区（县）所分配到的样本量将仅为第8个区（县）所分配到的样本量的2.3倍，这样可减少大规模区（县）样本量，增加小规模区（县）样本量，有效缩小各区（县）间样本量的差距。

此外，为了在一定程度上更好地反映各区（县）的情况，可规定各区（县）的最低样本量为100。按照人口规模平方根分配法分配的样本量少于100的增加至100，反之则不变。

2.2 城乡配额的确定

由于城乡环境差异较大，为了能切实反映全省范围内满意度的真实情况，保证样本在城乡分配上与实际情况一致，因此将各区（县）的样本量按城乡结构进行配额。

根据《中国统计年鉴2016》可知，2007—2015 年，A 省城镇化率持续稳步提升，在2015 年已超50%。考虑到方案设计的合理性及未来5年的实施效果，同时与该省的城乡比例保持一致，最终将6:4 作为全省的城乡基础配额比例。结合各区（县）具体的城镇化率，可进一步将全省各区（县）分为六类（分类标准如表2所示），并设定各类区（县）的城乡配额比例。经测算，各区（县）按该比例进行城乡配额可以保证全省样本量的城乡比约为6:4。

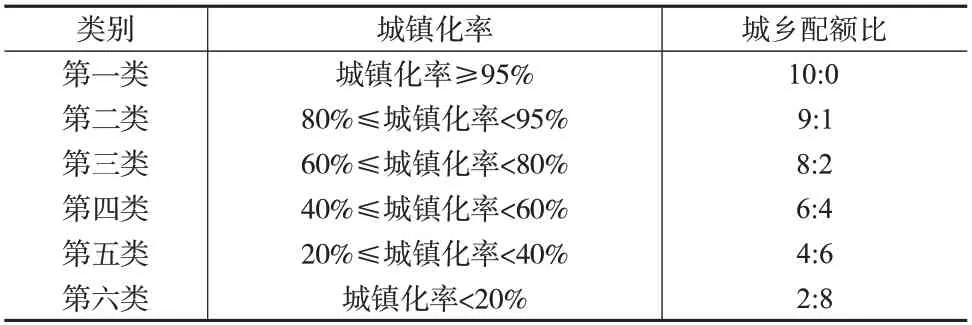
表2 各区（县）城乡配额比分类说明

2.3 年龄段配额的确定

在固定电话抽样中，抽取得到的样本平均年龄容易偏大。针对年龄段的设定，可参考全国人口的年龄总体分布①查阅《中国统计年鉴2016》。情况，设置18～39 岁、40～59 岁、60 岁及以上三个年龄段，这三个年龄段人群的配额比例分别为4:4:2。

2.4 二重抽样样本量的确定

本文采用二重抽样方法对无回答可能导致的误差进行补救。这里设定二重抽样样本量为无回答样本量的30%，在地级市（自治州）层面进行实现。

设地级市（自治州）内无回答样本量为n2，则该地级市（自治州）二重抽样的样本量m=n2×30%，该样本量m可在地级市（自治州）内各区（县）按便利原则分配，且保证地级市（自治州）二重样本的实际完成量至少达到150。

2.5 权数的计算和调整

由于抽样的随机性会导致抽取的样本结构与总体结构不一致，而结构不一致会导致推断精度下降，因此需要对样本权数进行调整，使样本结构与总体结构尽可能吻合。规模调整通过计算样本单元的设计权数以及无回答调整得到，结构调整通过对设计权数进行事后分层实现。权数的使用可以提高估计效果，但由于调整后的权数若差异过大，会增大估计量的方差，因此权数的使用中还涉及权数控制问题。

2.6 包含二重抽样的权数计算和调整

用W0ij表示第i个区（县）的第j个样本的设计权数，ni和Ni分别表示第i个区（县）所分配到的样本量和常住人口数量，则有。

2.7 权数的调整

采用二重抽样对样本中的无回答部分进行补救，无回答层中抽出的样本所代表的单元数目更大，需对其设计权数进行调整。根据二重抽样的样本量设计方案，无回答调整系数的计算需要与整个地级市（自治州）层面相对应。

设地级市（自治州）内无回答样本量为n2，二重抽样实际完成量为h，则第i个区（县）的第j个样本设计权数的无回答调整系数为：

因此，第i个区（县）的第j个样本的无回答调整设计权数为：

结构调整系数计算方法如下。以B市为例，假设调查数据按城乡和年龄两个变量分类的样本分布和总体联合分布如表3所示。

表3 B市基于城乡和年龄的样本分布 （单位：%）

以表3 中18～39 岁城镇单样本的15%为例，该值表示所抽取的样本集合中18～39 岁城镇样本的权数之和占全部样本权数之和的15%；对应单元格总体的值为24%，表示B 市实际总体中18～39 岁城镇居民占比为24%。由此可以看出，调查的样本分布与总体分布有所差别。与总体相比，样本中18～39岁人口偏少，60岁及以上人口偏多，城镇人口偏少，农村人口偏多。

本文采用迭代法对样本单元权数进行结构调整。两次迭代之后的调整结构与总体结构一致，得到基于城乡和年龄的最终结构调整系数r2ij，取值如表4所示。

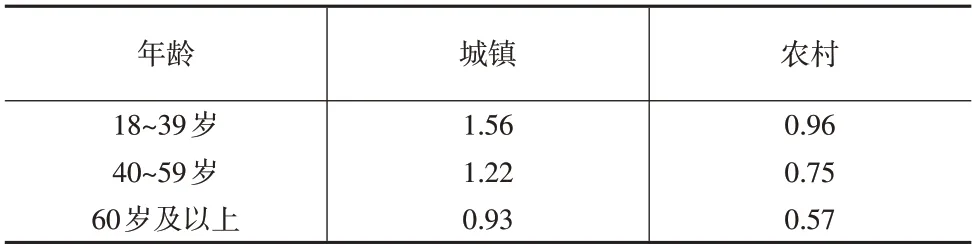
表4 B市基于城乡和年龄样本权数的系数调整结果

若两次迭代后得到的调整结构与总体结构仍然不同，则可按照上述方法继续调整，直至行与列的分布收敛于总体分布，得到最终的结构调整系数。由此，第i个区（县）的第j个样本的最终权数为：

经权数的无回答调整和结构调整，调查样本在规模和结构上能够还原总体。

2.8 权数的控制

为防止样本单元权数差异过大可能带来的估计量方差增大，有一些对权数进行控制的方法。本文使用相对简单的权数截取法对权数取值加以控制，具体如下：

当某个样本权数取值小于W的0.1分位点时，该权数取0.1分位点上的权数；当取值大于W的0.9 分位点时，取0.9 分位点上的权数；当处于二者中间时，权数取其本身。

但在实际调查过程中，由于时间、成本等因素未采用二重抽样方式处理无回答部分，而是采取直接删除，然后重新抽取样本单元进行覆盖的方法。这种方法虽然精度上有所下降，但是易于操作。那么第i个区（县）的第j个样本的最终权数为：Wij=W0ij×r2ij。其中，W0ij为设计权数，其权数结构调整系数r2ij的计算方法与前面包含二重抽样时的权数调整系数r2ij的计算方法相同。

2.9 目标估计量的估计

为方便之后的问题分析，对部分相关符号进行说明。

假设整个地级市（自治州）内有I个区（县），在第i个区（县）内（i=1,…,I），抽取ni个样本，将第一次调查回答单元组成的集合记为S1i，二重抽样回答单元组成的集合记为S2i，两次调查全部的回答单元组成的集合记为Si={S1i,S2i} 。

地级市（自治州）第一次调查回答单元组成的集合S1r={S11,S12,…,S1I}，二重抽样回答单元组成的集合S2r={S21,S22,…,S2I}，则整个地级市（自治州）内所有回答单元组成的集合可表示为：Sr={S1,S2,…,SI}。令K1r=|S1r|，K2r=|S2r|，Kr=|Sr|，即分别为集合S1r、S2r、Sr的单元个数。

Wij：第i个区（县）的第j个样本单元的最终权数。

yij：第i个区（县）的第j个样本单元的目标量得分。

N0：A省常住人口数量。

Nk：第k个地级市（自治州）的常住人口数量（k=1,2,…,21）。

2.9.1 采用二重抽样处理无回答部分

先从总体N中随机抽取n个样本单元，第一次调查有n1个回答单元和n2个无回答单元，则n=n1+n2；再从n2个无回答单元中随机抽取1 个容量为m的子样本进行第二次调查。

根据抽样估计原理，目标变量经过两个随机过程后，方差变为：

（3）地级市（自治州）满意度比例P的估计

令p1表示地级市（自治州）第一次调查中回答单元的样本满意度比例，p2表示二重抽样的样本满意度比例，则有p1=。其中，C是地级市（自治州）内具有某种特征的单元集合。地级市（自治州）满意度比例P的估计可以表示为：

全省21个地级市（自治州）均采用上述方法得到相应的估计量，以各地级市（自治州）的目标量估计结果为基础，可以得到全省的目标量估计结果。设第k（k=1,2,…,21）个地级市（自治州）的人口规模为Nk，其满意度均值的估计为，满意度方差的估计为,满意度比例的估计为。

（4）全省满意度均值的估计

（5）全省满意度方差的估计

（6）全省满意度比例Pz的估计

2.9.2 未处理无回答部分

在实际调查中，由于时间和成本的限制，以及各地级市（自治州）的执行情况，因此未进行二重抽样，此时的真实情况为：Sr为仅包含初始调查时所有回答单元的集合；Wij为不进行二重抽样时的最终权数，即Wij=W0ij×r2ij。其中，W0ij为第i个区（县）的设计权数；r2ij为权数结构调整系数，其计算方法与前面包含二重抽样时的权数调整系数r2ij的计算方法相同。

（1）地级市（自治州）满意度均值的估计

（2）地级市（自治州）均值估计的方差估计

其中，f=为抽样比。

（3）地级市（自治州）满意度方差S2的估计

（4）地级市（自治州）满意度比例P的估计

（5）全省满意度均值的估计

（6）全省均值估计的方差估计

（7）全省满意度方差的估计

（8）全省满意度比例Pz的估计

3 实例

《A省满意度调查》采用电话调查的方式，覆盖了全省所有地级市（自治州）所辖的183 个区（县），共收集到33760 份有效问卷。其中，目标估计量的计算包括全省、各地级市（自治州）以及各区（县）目标估计量的均值和标准差。具体的计算过程如下。

3.1 权数计算和调整

在《A 省满意度调查》中，由于保密原因，因此只在各地级市（自治州）层面上和各区（县）层面上，对目标估计量进行对比分析。在人口规模已知的条件下，本文采用标准化权数调整的方式，对各地级市（自治州）及全省的权数进行调整，这样做的目的在于使样本还原总体，即样本单元的权数之和等于总体规模。

无论是各地级市（自治州）的权数调整，还是全省的权数调整，都包括了两个步骤。以各地级市（自治州）为例：

第一步，将各区（县）的人口规模除以其相应的样本量，即可得到各区（县）的设计权数。

第二步，将第一步得到的结果乘以其对应地级市（自治州）的样本总量除以人口规模的值，即乘以其对应地级市（自治州）的抽样比例。

用设计权数乘以抽样比例，就是权数标准化的核心。之所以要对权数进行标准化，是因为在后续的数据处理过程中，需要用现有的样本总体代替原有的抽样框，而标准化的过程就是将样本还原成总体的一个过渡。

3.2 估计量标准差的计算

利用前面得到的权数，结合Jackknife（刀切法）来分别计算全省、各地级市（自治州）以及各区（县）的均值和估计量的标准差。

本次采用的是弃1-刀切法，其核心思想是先每次去掉一个值，再计算剩余样本的标准差，重复n（n为对应的样本量）次以后，可以得到n组不同的样本，最后的标准差等于各组样本标准差的均值，而均值是加权均值。

通过以上方法计算得到的均值和标准差精度较高，全省满意度的均值为83.50%，总标准差为0.384%，相对误差约为0.90%。各地级市（自治州）满意度的均值都在75%以上，标准差基本上在0.01 附近波动，相对误差在3.10%以内，具体数值如表5所示。

表5 A省各地级市（自治州）满意度的均值和标准差对比结果

计算结果显示，加权后部分地级市（自治州）满意度的均值有所降低，但也有个别地级市（自治州）满意度的均值是增加的。总的来说，减少的比增加的多，所以加权以后，在全省层面上，满意度的均值是降低的。而正因为加权以后整体的离散性变大了，所以各地级市（自治州）的标准差都呈现上升的趋势。

此外，根据本次调查所收集到的原始数据计算得到满意度的方差约为0.2，这与原先方案中设计的方差0.3 差别不大，与绝对误差3%吻合，说明抽样数据质量较高，计算方法优良。

4 结论

本文探讨了分层抽样技术的重要性和广泛应用，结合《A 省满意度调查》的背景要求也提出了利用二重抽样的方式来解决电话调查中的缺失数据问题，结合实例对每个层中的样本量分配、权数计算和控制、样本的计算进行了详细的分析，并比较了采用二重抽样和不采用二重抽样情况下权数的调整方法，并推导出了实际目标估计量的计算公式。在地级市（自治区）层面上，借助辅助变量的信息，利用迭代法和事后分层相结合的方法对样本权数进行调整，使样本结构和总体结构一致。最后，结合具体的调查数据证实了所提方法的有效性，在一定程度上提高了估计的精度。