基于Python的最小二乘法在电子天平中的应用

【摘要】本文通过分析在不同电子天平上应用最小二乘法的算法来修正电子天平的误差，使其能够满足计量检定要求，通过读取不同电子天平的检定数据后在Python上对其进行各种数据分析和计算，利用最小二乘法进行曲线拟合得出相对应的系数，然后代入公式计算出其修正后的误差。通过对不同电子天平的对比来发现问题来解决电子天平应用中的实际问题。

【关键词】电子天平；最小二乘法；Python

【DOI编码】10.3969/j.issn.1674-4977.2023.06.056

【基金项目】甘肃省市场监督管理局科技计划资助项目：电子天平检定管理系统研究与开发（SSCJG-JL-B202202）。

Application of Least Squares Method Based on Python in Electronic Balance

AN Minjun

（Gansu Institute of Metrology， Lanzhou 730050， China）

Abstract： This article analyzes the application of the least squares method algorithm on different electronic scales to correct the error of the electronic balance， so that it can meet the requirements of metrological verification. By reading the calibration data of different electronic balances and conducting various data analysis and calculations on Python， the least squares method is used to fit the curve to obtain the corresponding coefficients， and then the corrected error is calculated by incorporating the formula. By comparing different electronic scales to identify problems and solve practical problems in the application of electronic scales.

Key words： electronic balance； least squares method； python

电子天平作为非自动衡器，特别是作为机械天平的替代物。一般采用應变式传感器、电容式传感器、电磁平衡式传感器。应变式传感器，结构简单、造价低，但精度有限；电容式传感器称量速度快，性价比较高，但无法达到很高的精度；采用电磁平衡传感器的电子天平，其特点是称量准确可靠、显示快速清晰并具有自动检测系统、简便的自动校准装置以及超载保护等装置。电子天平被称作电子和机械相结合的产物。随着现代工业的发展，称量系统的应用越来越广泛，特别是电子天平的应用，电子天平作为现代称量系统的核心部件，起到了不可或缺的作用。作为电子和机械相结合的产物，电子天平在使用一段时间后，由于受机械变形或者电子元器件老化等各种原因，导致电子天平各种性能下降，一般通过两点标定来修正其系统误差，但是有些电子天平的传感器其线性比较差，不能很好地解决此类问题，本文通过利用最小二乘法的算法，通过多点采集可以解决传感器线性不太理想的此类问题，分析最小二乘法最适合于在哪种情况下的应用。

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。最小二乘法还可用于曲线拟合，最小二乘法是一种广泛应用的算法，在最优控制等各种控制系统和预测中都有应用。本文通过其可用于曲线拟合来计算修正系数。

本文以分别用厂家为赛多利斯科学仪器（北京）有限公司、梅特勒-托利多仪器（上海）有限公司、RADWAG，型号为BSA224S、MS204TS/02、AS220.R2的三台220 g的万分之一电子天平为例，分别采集0 g、0.1 g、10 g、20 g、50 g、100 g、200 g、220 g八个点的检定数据，数据如表1。

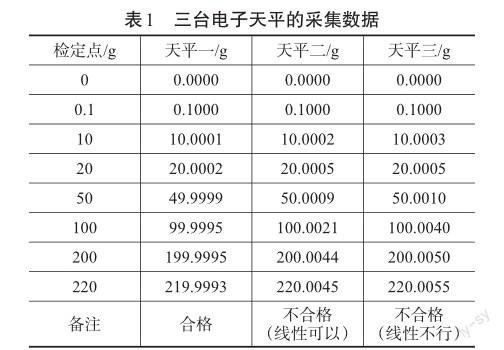
由于python语言具有开放性，可以灵活应用，很多源代码都是公开的，适合于各个学习阶层，利用网络资源上的开源代码就可以解决。利用其开源代码，调用numpy库，就可以利用python对其进行数据分析及计算[2]。其中的matplotlib库可以将数据可视化，便于观察发现问题。scipy是一个高级的科学计算库，可以很方便对数据进行迭代运算。通过调用这几个库，特别是numpy和matplotlib库，实现了数据分析及其可视化，便于发现问题，使其更加直观。其程序如下。

2.2数据分析

对于电子天平来说，作为一个称重系统，出厂最理想的建模输出函数应该为y=x，但是由于在使用过程中由于其传感器的变形、电子元器件的老化以及使用中电压和环境等各方面因素的影响，其输出函数已经不是理想状态下的y=x，本文我们通过一阶函数y=kx+b对其进行拟合，分别对3个天平的输入和输出进行一阶函数y=kx+b的曲线拟合，如图1所示。

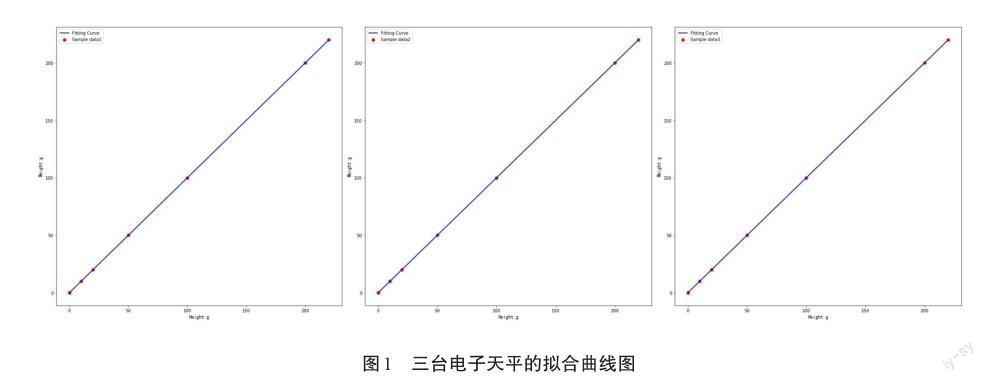
然后我们通过对已采集到的八个点输入到一阶函数y= kx+b进行验证，并且同时在将修正值加上后得到其修正后的误差，其修正值为测量值减去标准值。如表3。

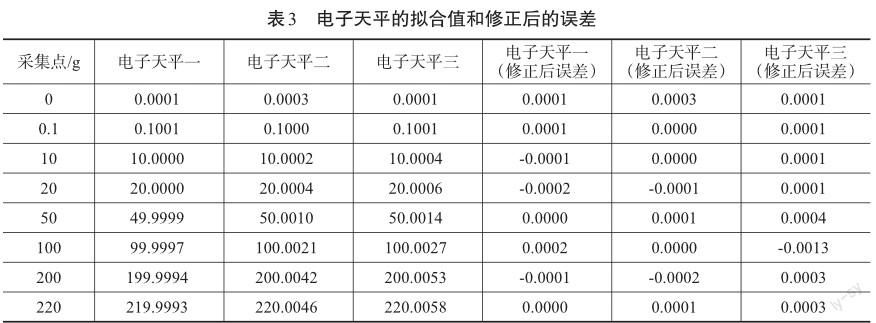
通过对表3的电子天平修正后误差可以看出来，电子天平修正后电子天平三在100 g这个点不合格，但是对于线性可以的电子天平具有较好的补偿作用，所以最小二乘法对于线性好的电子天平具有較好的补偿修正作用。电子天平一的检定点是检定合格的，其修正以后误差非常小；电子天平二的检定点是不合格，但是其传感器线性可以，通过修正以后误差也是非常小；电子天平三的检定点也不合格，其传感器线性在小量程不好，经过修正后其100 g这个点不合格，通过对比分析，发现传感器在局部非线性时，不能很好地解决此类问题，这就需要控制中的鲁棒控制、神经网络、专家系统等各种先进控制算法。

【参考文献】

[1]曹连江.电子信息测量及其误差分析校正的研究[M].长春：东北师范大学出版社，2017-09.

[2]王立友.基于Python的线性回归最小二乘算法的设计与实现[J].电脑知识与技术，2021，17（35）：123-124，133.

[3]丁克良，欧吉坤，陈义.整体最小二乘法及其在测量数据处理中的应用[C]//中国测绘学会.中国测绘学会第九次全国会员代表大会暨学会成立50周年纪念大会论文集.2009：406-412.

[4]姜伟，付佳媛.最小二乘法及其应用[J].中国传媒大学学报（自然科学版），2020，27（5）：72-78.

[5]李蓉，张一帆，杨薇薇.基于最小二乘法和卡尔曼滤波算法的平面电子罗盘误差补偿方法研究[J].宿州学院学报，2019，34（11）：77-81.

【作者简介】

安民军，男，1981年出生，高级工程师，硕士，研究方向为计量检定。

（编辑：侯睿琪）