长江中游城市群31市物流竞争力层级划分

石学刚，罗 荣

（1.中国民航大学临空经济研究中心，天津 300300；2.中国民航大学 交通科学与工程学院，天津 300300）

0 引言

近年来，长江中游城市群的产业结构正在转型升级，城市群内部各城市间的物资交换愈加频繁，物流产业发展在城市经济发展过程中扮演着重要角色。考虑到该地区物流发展中存在辐射效应不足、物流资源闲置等问题，需要进一步对城市群内部城市进行层级划分，以期更好地应对物流产业的发展。

1 评价指标体系筛选

对长江中游城市群的31个节点城市进行层级划分，首先需要选取合理的评价指标全面评价各城市的物流竞争力。结合该城市群物流特征和物流发展的实际需求，从城市经济发展水平、物流产业规模、物流需求和物流发展潜力四个方面构建指标体系。

在对城市物流竞争力的研究中，常使用城市三大产业产值及地区生产总值来描述城市的经济发展水平[1]，增加第三产业产值占比及进出口贸易总额来突出物流业相关经济。在物流产业规模指标选取中，常使用货运量、货物周转量等指标进行评价[2]，在此基础上，增加物流业从业人员数量考察城市的物流产业规模。此外，人均可支配收入、社会消费品零售总额等指标可以体现城市对物流发展的需求[3]；城市的信息化水平及城市每年各产业产值的增长率等指标可以很好地描述城市物流的发展潜力[4]。根据城市群物流竞争力评价指标体系的构建原则，初步选取了4个一级指标和22个二级指标作为长江中游城市群物流竞争力评价的具体指标，见表1。

使用2021 年各城市的《统计年鉴》和2016-2020 年的《国民经济和社会发展统计公报》，经因子分析法得到的四个一级指标层（经济发展水平、物流产业规模、物流需求、物流发展潜力）旋转后累计方差解释率分别为99.75%、71.54%、93.63%、85.81%，信息提取量均大于50%，各一级指标层旋转后因子载荷系数分别见表2-表5。

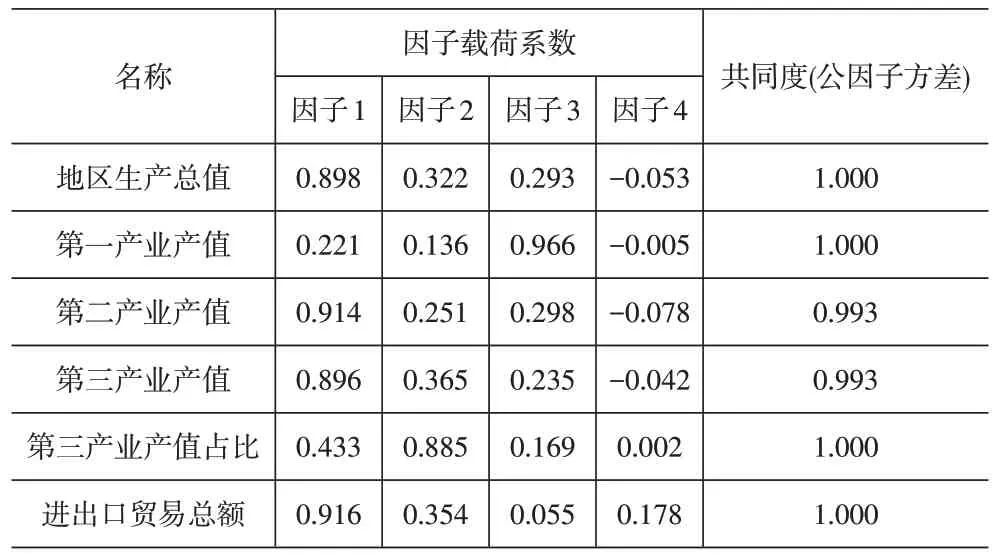
表2 旋转后因子载荷系数-经济发展水平

由表2可得，第一产业产值在因子1中的因子载荷系数绝对值小于0.4，将该指标删去；第三产业产值占比在因子1中的因子载荷系数绝对值虽大于0.4，但其在因子2中的值远高于在因子1中的值，故将该指标也删去。综上，经济发展水平由地区生产总值、第二产业产值、第三产业产值和进出口贸易总额这4个二级指标表示。

由表3可得，各指标因子载荷系数绝对值均远大于0.4，故所有指标均保留。即物流产业规模由物流从业人员数量、公路货运量、铁路货运量、水运货运量、民航货运量、货运周转量这6个二级指标表示。

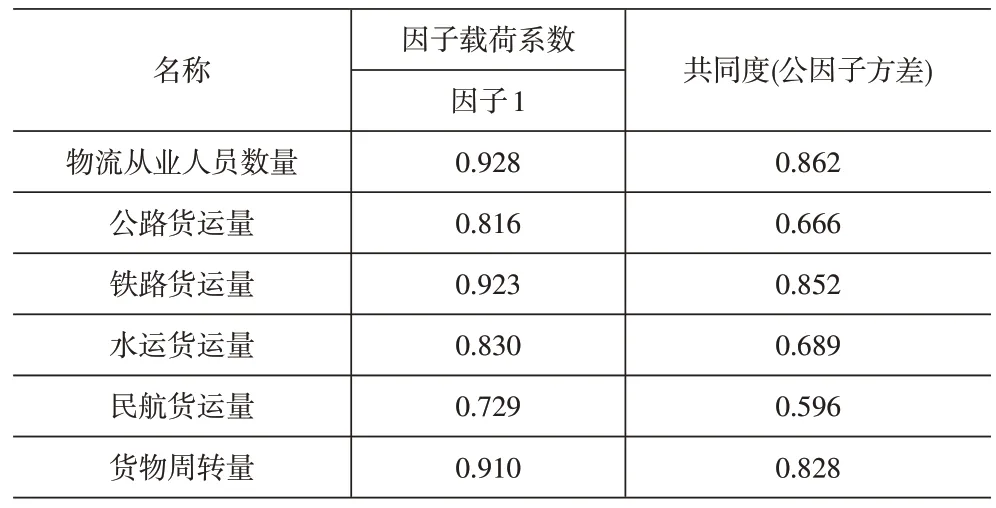
表3 旋转后因子载荷系数-物流产业规模

由表4可得，年末常住人口数在因子1中的因子载荷系数绝对值小于0.4，将该指标删去；其余指标在因子1中的因子载荷系数绝对值远大于0.4，故保留其余指标。综上，物流需求由社会消费品零售总额、城镇常住居民人均可支配收入、邮政业务总量这3个二级指标构成。

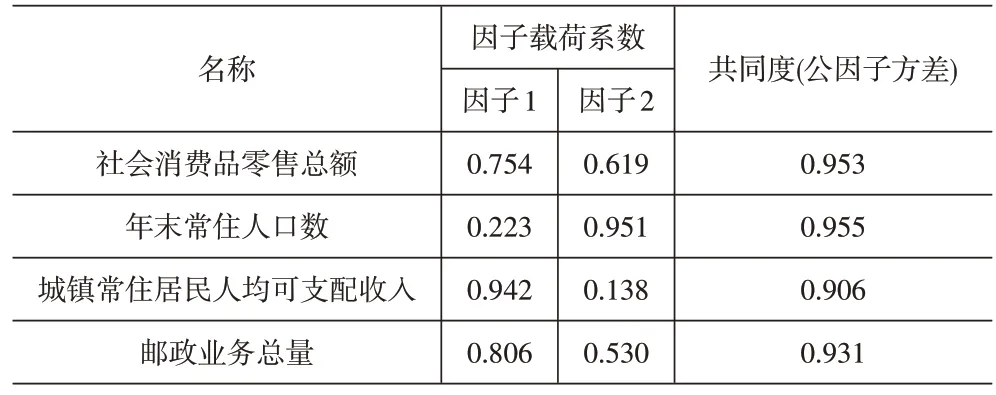
表4 旋转后因子载荷系数-物流需求

由表5可得，地区生产总值增长率、第三产业产值增长、进出口贸易总额增长率在因子1中的因子载荷系数绝对值小于0.4，将这些指标删去；其余指标在因子1中的因子载荷系数绝对值远大于0.4，故保留其余指标。综上，物流发展潜力由互联网接入用户、普通高等院校数量、普通高等学校在校生数这3个二级指标构成。

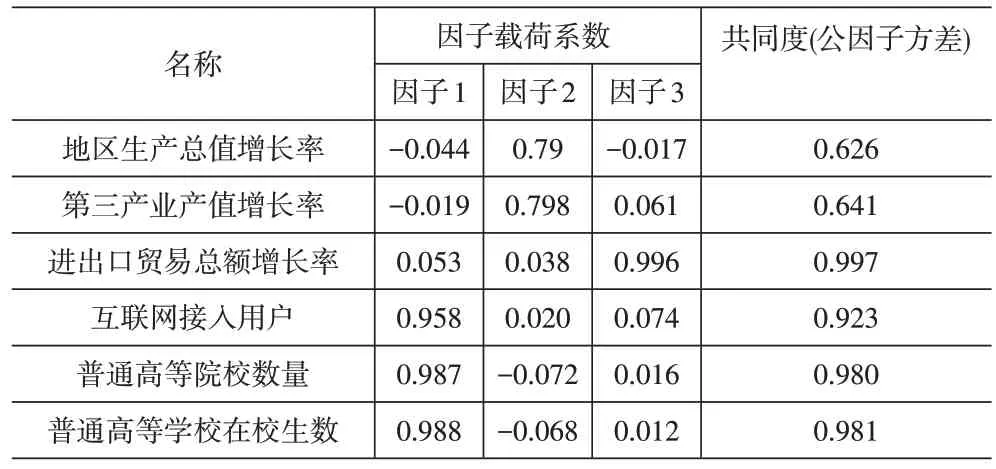
表5 旋转后因子载荷系数-物流发展潜力

通过因子分析法对各指标的因子载荷系数绝对值进行分析，同时考虑各指标的数据可获得性，最终从经济发展水平、物流产业规模、物流需求、物流发展潜力四方面出发，选取16个指标评价长江中游城市群各城市的物流竞争力，见表6。

表6 城市物流竞争力评价指标体系

2 两阶段熵权-TOPSIS方法介绍

2.1 熵权法

评价结果很大程度上取决于评价指标的权重。AHP和德尔菲法是常用的主观评价方法，但这两种方法存在着很大的不确定性和个人主观因素；客观赋权法主要有熵权法、因子分析法等，这类方法能根据评价对象的实际情况更好地反映各指标的权值。在此基础上，利用熵权方法对各评价指标进行赋权。

步骤一：设在城市物流竞争力评价指标体系中，有m个待评价城市，n项竞争力评价指标，构建出原始数据的评价矩阵为X=[xij]m*n，即：

步骤二：数据的标准化处理，公式如下：

步骤三：确定竞争力评价指标权重Yij：

步骤四：第i个评价指标的熵ej为：

步骤五：计算信息熵冗余度：

步骤六：第j个城市指标的熵权wj为：

2.2 TOPSIS法

TOPSIS又称优劣距离法，是一种能有效解决多目标决策问题的方法。TOPSIS法在多个选择对象中选择最优解和最劣解，通过计算其与待评价对象之间的欧式距离，判断相对最优解。评价步骤如下：

步骤一：根据评价对象原始数据构造标准化权重矩阵：

步骤二：确定正负理想解：

步骤三：计算各方案到正理想解的距离：

步骤四：计算各方案到负理想解的距离：

步骤五：计算各方案与理想解的相对贴近度：

2.3 两阶段熵权-TOPSIS

熵权-TOPSIS法的使用需要大量的数据，在研究中，部分数据的获取难度较大，只能通过插值法等方法来获得估算数据，两阶段熵权-TOPSIS法的使用可以在一定程度上解决该问题，并且可以根据评价指标的优先级来对第一阶段和第二阶段的指标加以区别，具体步骤如下：

步骤一：确定研究对象个数和指标体系。研究对象为长江中游城市群所包含的31个城市，城市物流竞争力评价指标体系见表1。

步骤二：确定城市层级。在节点城市的初步层级划分中将31个城市划分为中心城市和其余节点城市两类，其中中心城市占比为20%，即取排名前6的城市为中心城市，其余25个城市为节点城市。

步骤三：收集城市物流竞争力评价指标体系的数据，包括城市经济发展水平、物流产业规模、物流需求。

步骤四：第一阶段，熵权-TOPSIS模型用于计算长江中游城市群31个城市的综合排名，根据步骤二中确定的中心城市个数，选择排名前8的城市，作为中心城市的候选城市。

步骤五：收集中心城市候选城市物流发展潜力的相关数据，连同城市经济发展水平、物流产业规模、物流需求的相关数据作为第二阶段的指标体系。

步骤六：第二阶段，再次使用熵权-TOPSIS模型计算8个中心城市候选城市的排名，选择排名值前6的城市作为中心城市。

3 两阶段城市层级划分

相关数据来源于2021年各城市的《统计年鉴》和2016-2020 年的《国民经济和社会发展统计公报》。结合上述数据，运用两阶段熵权-TOPSIS方法进行分析，计算长江中游城市群所包含的31个城市的物流竞争力，并对此进行排名。第一阶段：基于城市经济发展水平、物流产业规模、物流需求相关指标计算31个城市物流竞争力，所得结果见表7。

据表7可得，长江中游城市群物流竞争力排名前8位的城市有武汉、长沙、南昌、襄阳、宜昌、岳阳、常德、衡阳。其中，武汉、长沙、南昌的竞争力得分以0.3左右的差距依次下降，这表明武汉在31个城市群中最具竞争力，其次是长沙、南昌；其他城市的排名得分差距相对较小，表明除三个省会城市以外，该城市群内部各城市的物流发展较为均衡。在排名前50%的城市中，湖北有6个，湖南和江西分别各有5个，在长江中游城市群的分布相对分散，更有利于城市群内部协作。

第二阶段：增加城市物流发展潜力相关数据，对第一阶段的8个中心城市候选城市物流竞争力进行再次排名，所得结果见表8。

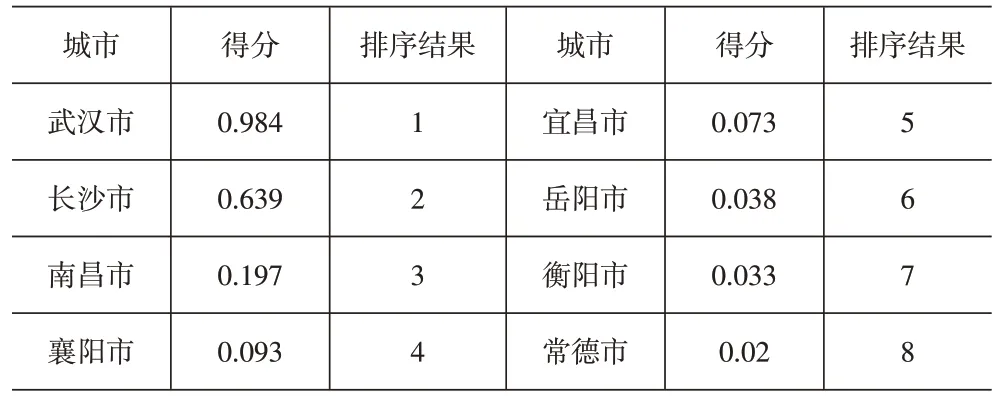
表8 长江中游城市群中心城市候选城市物流竞争力排名

结合表7和表8的分析结果可以直观地看出，增加物流发展潜力这一评价指标后，城市之间物流竞争力的差距相对明显。除去省会城市，襄阳、宜昌的物流竞争力优势相较岳阳、衡阳、常德这三个城市更加显著。在第二阶段的城市群物流竞争力排名中，武汉、长沙、南昌居于前三，推动长江中游城市群物流业的协调发展。综合实力较强的三个省会城市担任中心城市的角色，拉动相连节点城市物流业的发展；襄阳、宜昌和岳阳这三个城市的发展紧随其后，与中心城市差距较小，宜作为城市群物流发展的副中心城市。

综合两次竞争力评价结果，常德、衡阳、株洲、九江、荆州、宜春、上饶、黄冈、孝感、湘潭的发展处于第二层级，这些城市本身经济发展水平较好，具有较大的发展潜力，可为边缘城市的发展提供支持。吉安、荆门、黄石、益阳、娄底、咸宁、抚州、鹰潭、鄂州、萍乡、景德镇、新余、仙桃、潜江、天门这些城市的物流发展水平较低，可为第一层级和第二层级城市的物流业发展提供“后勤”服务。

综上所述，确定武汉、长沙、南昌为中心城市，襄阳、宜昌、岳阳为副中心城市，常德、衡阳、株洲、九江、荆州、宜春、上饶、黄冈、孝感、湘潭为主要节点城市，吉安、荆门、黄石、益阳、娄底、咸宁、抚州、鹰潭、鄂州、萍乡、景德镇、新余、仙桃、潜江、天门为次要节点城市。

4 长江中游城市群发展建议

针对上述研究，为促进长江中游城市群物流发展提出以下几点建议：

第一，充分发挥武汉、长沙、南昌三个中心城市的物流枢纽作用，加强对外辐射能力。

第二，充分利用襄阳、宜昌、岳阳三个副中心城市的物流资源优势，加强其相关物流通道的建设，激发副中心城市周边城市的物流潜力。

第三，主要节点城市和次要节点城市的发展也可以缓解中心城市物流通道拥挤、物流承载过大等问题。贯通节点城市到中心城市的物流走廊，强化节点城市的物流覆盖，有利于建设多层次、现代化、一体化的城市群物流网络。