安家岭煤矿爆破振速预测与安全允许距离研究

李 辉，王董东，杜文康，弓 煜

(中国矿业大学(北京)力学与建筑工程学院，北京 100083)

对于大规模露天开采，工程爆破是最为经济有效的手段[1]。在爆破作业中炸药爆炸会释放出巨大的能量，所产生的地震波会对周围建筑物以及边坡岩体带来负面影响[2]，对地震波的传播进行准确预测，可以降低或避免其产生的影响，因此对爆破地震波的衰减规律进行研究是非常必要的。

近年来，许多爆破工作者针对爆破振动对周围建筑物的影响进行了深入的研究和探讨。胡平[3]等通过对已有爆破设计进行优化，采用了改变掏槽型式、打设减震孔及增加爆破自由面等方法，把地表建筑物的峰值振速控制在安全范围内，解决了爆破振动对建筑物产生的安全问题；丁新宇[4]等对砖混结构建筑物的不同楼层进行长期监测，研究了爆破振动下建筑物的响应规律，从频率的角度分析了不同高度的楼层随爆破振动的变化情况；瞿东明[5]等考虑了高差影响下的振动衰减规律公式，并使用该公式对隧道沿线的地面建筑进行安全评估，结合允许振速分析了不同围岩等级下的安全评价结果。

针对矿山爆破振动，爆破学者也进行了大量的研究。胡方强[6]等采用回归分析的方法得出了爆破振动的衰减规律，选取最不利因素对测点振速进行反算，并验证了K和α的可靠性，计算出不同最大单孔药量下爆破点到房屋的最近距离；赵学龙[7]等选取垂向振动速度对矿内振动情况进行预测，分析了预测值与真实值的误差，把建筑物所在处的最大振速控制在0.7 cm/s以内，确保爆破振动不会对周围建筑物产生安全影响。刘滨[8]等结合振动速度和主频分析了地下开采对地表建筑物的影响，并验证了回归模型的准确性；刘玉福[9]等分别分析了考虑高程影响下和未考虑高程影响的两种爆破振动公式的两种形式，通过相关性分析验证了爆破振动速度存在高程放大效应。

爆破学者在许多领域取得了大量成果和科研进展，为爆破作业的顺利进行和人民的生命财产安全做出了重大贡献。安家岭煤矿目前也面临建筑物安全问题，对重要建筑物进行振动监测，掌握安家岭煤矿爆破地震波的传播规律，在前人研究的基础上，通过引入安全系数准确计算煤矿与周围建筑物的安全距离是目前急需解决的问题。

1 安家岭煤矿工程概况及爆破设计

中煤平朔集团有限公司安家岭露天煤矿位于山西省朔州市境内，是国内大型露天矿山，矿山开采主要在芦子沟背斜上部，工作面正在向东推进，东帮矿界近距离内存在白芦煤矿办公楼、职工宿舍、平朔至陶村乡公路等重要建筑及基础设施。目前安家岭露天煤矿正在面临靠近开采边界问题，爆破作业已经对部分建筑物产生影响，引起了民企纠纷，影响了爆破作业的正常进行。

1.1安家岭煤矿工程概况

安家岭煤矿位于宁武煤田北部区域，2003年7月投入生产，主要开采区域为4#煤层、9#煤层和11#煤层，东帮矿区地层主要由黄土、亚黏土、泥岩、砂岩、砂质泥岩和煤等组成，节理发育较差，岩体完整性良好，含水量相对较小，岩石力学参数见表1。

表1 安家岭煤矿岩石力学参数

1.2 爆破设计

安家岭矿山采用混装炸药装药爆破，反向爆破，孔间延期25 ms，排间延期65 ms。设计台阶高度为15 m，孔深约16.5 m，采用方形布孔，孔距与排距一般为6～8 m，炮孔直径为160和250 mm，堵塞长度5～8 m，使用连续耦合装药结构，并使用岩粉填塞炮孔。装药结构和爆破区域切面如图1所示。

图1 装药结构和爆破区域剖面

2 爆破振动监测

2.1 测振仪选取与测点布置

爆破振动监测采用成都中科测控有限公司生产的TC-4850爆破振动记录仪和TCS-D3三分量速度传感器，仪器参数的设定为：采样频率2000 Hz，触发模式采用内触发，触发电平0.05 cm/s，触发延时-100 ms，采样时间5 s。为了使得监测结果更准确，测振仪器均使用强力快粘粉布置在墙角坚固处，并用水准仪确保传感器水平安放。

2.2 监测方案

矿区东帮建筑物和基础设施较多，为了准确计算东帮爆破边界的安全距离，本次所选取的测点为较近的重要建筑物，共设置四个测点，分别为测点一白芦主工业广场办公楼、测点二白芦主工业广场职工宿舍、测点三白芦副工业广场保安室、测点四白芦副工业广场大门。监测点和爆破作业区域位置如图2所示，共对12个爆区的爆破振动进行了监测，获得了43组数据。

3 爆破振动数据分析

3.1 质点峰值速度分析

测试完成后，对监测数据进行整理，爆破振动峰值速度部分数据见表2，典型爆破振动波形如图3所示，该测点布置在主工业广场办公楼，反映了爆破时该点的爆破振动速度变化情况，其中X方向为水平径向(指向爆破中心方向)，Y方向为水平切向(垂直于爆破中心方向)，Z方向为竖直方向。由于地形变化明显，在几次振动监测中，质点振动峰值速度变化相对较大，总体变化情况为随着监测点与爆破中心距离增大时，振速逐渐较小。

图3 典型爆破振动波形

表2 爆破参数与振动监测数据

在计算爆破振动质点峰值速度时，爆破学者主要采用的是使用经验公式进行回归分析，国内最广泛使用的是苏联学者总结的萨道夫斯基公式[10，11]：

V=K(Q1/3/R)α

(1)

式中，V为建筑物所在地质点峰值振速，cm/s；Q为延时爆破时的最大单段药量，kg；R为建筑物所在地到爆破中心的距离，m；K、α为爆破中心与建筑物所在地的地形、地质条件和爆破条件有关的系数和衰减指数。

在对质点振动峰值速度拟合时，通常将萨道夫斯基公式转化为一元线性回归进行分析[12，13]，式(1)两边同时取对数后，可变形为：

lnV=αln(Q1/3/R)+lnK

(2)

令y=lnV，x=ln(Q1/3/R)，b=lnK，式(2)则可变形为一元线性方程的形式：

y=αx+b

(3)

对爆破振动监测数据进行整理，为了得到爆破振动的传播规律，采用一元线性回归方程进行回归分析，将监测所得的相关数据进行拟合，拟合结果如图4所示。

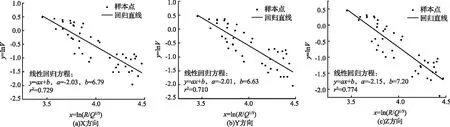
图4 质点振动速度拟合结果

对43组监测值进行线性回归分析，得到的萨道夫斯公式分别为：

Vx=888.914(Q1/3/R)2.03

(4)

Vy=757.482(Q1/3/R)2.01

(5)

Vz=1339.431(Q1/3/R)2.15

(6)

由于爆破区域与建筑物之间存在的沟渠和公路起到了一定的减振作用，地质条件较为复杂，爆破地震波传播路径上地形与地质参数变化较大，因此将回归分析得到的K值和α值与《爆破安全规程》(GB 6722—2014)[14]中的参考值进行对比，二者存在差别，现场试验中的参数应根据地质条件和爆破参数及时调整[15-17]。回归公式的相关系数r均大于0.8，说明监测数据的离散性较小，通过变形后的萨道夫斯基公式对数据进行线性回归拟合是可靠的，能够反映安家岭煤矿爆破时建筑物附近的质点振动情况，回归结果能够应用于安家岭煤矿的工程需求。

3.2 质点振动峰值速度预测与分析

通过线性回归得到的萨道夫斯基公式对爆破质点振动峰值速度进行预测，再对安家岭煤矿爆破作业进行监测，共计得到20组数据，把预测值与安家岭煤矿爆破作业时建筑物所在处的质点振动峰值进行对比，部分数据见表3，分析预测值与监测值的绝对误差，可得出并非所有的监测值都低于实测值，X、Y、Z方向质点振动峰值速度实测值大于预测值的百分比分别为35%、30%、35%。可见，通过传统的经验公式只能对质点振动峰值速度进行一定范围内的预测，无法保证建筑物的安全状态，为了矿区的顺利生产且不对既有建筑物带来安全隐患，需要引入安全保证系数进行计算。

表3 实测值与预测值对比

4 爆破振动安全允许距离确定

4.1 质点振动峰值速度预测

在通过萨道夫斯基公式进行质点振动峰值速度预测时，预测值与实测值会存在较大误差[18]，即令某一点的预测值为y，实测点的预测值为Y，则该点的预测值与实际值之间的关系可以表示为：Y=y+ε，式中，ε为误差值。ε为随机误差，其值的大小与正负是不可控的，因此，预测所得到的振动速度可靠性较低，若通过该值确定最小安全距离，则会对建筑物的安全带来较大隐患。梁书峰等[19]通过理论分析与工程实践相结合，得出了基于可靠性指标的经验式如下：

式中，ε为预测值与实际值之间的误差；n为监测的数据个数；β为显著性水平；tβ/2(n-2)为在可靠性指标为(1-β)的情况下的t-分布；r为相关性系数。

为保证建筑物的安全，分别取1-β=95%和1-β=99%，即在置信区间为95%和99%下求得ε值，由于预测振动速度对建筑物的影响，故只需计算出右侧置信区间即可，计算结果见表4。

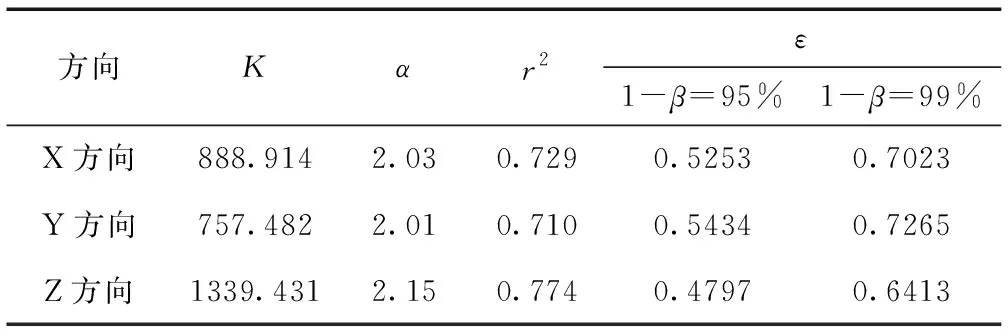
表4 各参数计算值

通过表4计算出的结果与式Y=y+ε与线性回归结果对比，计算如图5所示，可以看出在X方向、Y方向与Z方向上取置信度1-β=95%时，预测直线不能完全包络样本点，此时不能保证建筑物处于安全的状态，随着安家岭煤矿的工作面向东推进，质点峰值振速有超出包络线的可能，即随着爆心距的减小，预测值可能会接近甚至超过预测曲线；当置信度取1-β=99%时，样本点能够较好地被预测直线包络。因此，为了周围建筑物安全状态能够得到更好的安全保障，置信度1-β=99%时更为可靠的。

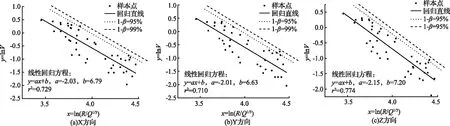
图5 置信水平为95%和99%计算

4.2 最小安全允许距离确定

根据《爆破安全规程》(GB 6722—2014)评估爆破振动对保护对象的振动影响时，需结合质点振动峰值速度与振动主频进行判定，安全允许质点振动速度见表5。监测地点处存在民用建筑和工业建筑，经过对比，为使建筑物都处于安全状态，应取最不利组合。由于爆破地震波在传播时高频成分振动波衰减较快[20，21]，且结合监测结果，建筑物所在处的主频多分布在0～10 Hz，所以在确定最小安全距离时，综合考虑保护对象类别和振动主频，安全允许质点振动速度取2 cm/s较为合适。

表5 安全允许振动速度

对式Y=y+ε，其中Y=lnV，y=αx+b，x=ln(Q1/3/R)。进行变形可得：

带入已知参数可得：

式中，Rx、Rx、Rz分别表示X方向、Y方向、Z方向在最大单段药量为Q时的安全允许距离。

安家岭露天煤矿爆破作业采用的最大单段药量主要为402、616、748、836 kg。利用上述安全允许距离公式对最小安全距离进行计算(表6)可得：当最大单段药量分别为402、616 、748和836 kg时，对应的最小安全距离为210.22、242.36、258.56和268.33 m。预测数据可为安家岭矿界向东推进时提供理论依据，同时为类似工程提供理论参考。

表6 不同单段药量下安全允许距离值

5 结 论

1)采用一元线性回归方程对监测数据进行分析，得到的质点振动峰值速度预测公式相关性较好。

2)预测建筑物所在处质点峰值振速时，引入安全保证系数能够较好地保证建筑物处于安全状态。置信区间1-β=99%与1-β=95%相比更具优势，预测直线能够完全包络样本点，更具有可靠性。

3)由于爆破地震波传播路径上地形和地质条件较为复杂，因此回归分析所得到的K值和α值与《爆破安全规程》相比存在一定的差异，为了更好地反映实际情况应采用现场试验测定值。

4)结合安全保证系数和《爆破安全规程》对于一般民用建筑的安全振速允许值，确定出三方向最小安全距离公式分别为Rx=28.484Q1/3，Ry=27.513Q1/3，Rz=27.791Q1/3，并计算出不同最大单段药量下的安全距离。也可通过公式计算，在爆心距确定的情况下及时调整最大单段药量，为矿区的生产和周围建筑物的安全提供参考。