大型机场单通道U型机坪区推出等待点优化设计
2023-11-04李治寒朱新平张天雄陈洪浩
李治寒, 朱新平, 张天雄, 陈洪浩
(中国民用航空飞行学院空中交通管理学院, 广汉 618307)
全球民航逐步恢复并迎来快速发展,传统的飞行区场面运行保障压力将逐步增加,而由此导致的航班延误和场面冲突问题也将日益凸显,采用机场改扩建增加保障资源供给能力因其耗资耗时,或场地受限往往难以实施或快速奏效。鉴于此,对场面关键区域的运行程序进行优化,成为经济有效的解决办法。
对于场面运行优化,徐川等[1]使用模糊C均值聚类算法(fuzzyC-means, FCM)确定预测的拥堵状态数据聚类中心,对拥堵状态进行分类确定场面拥堵状态等级,为管制员提供了宏观层面的决策信息。朱晓波等[2]改进反向传播(back propagation, BP)神经网络,能够更加精确地对航空器滑行时间进行预测。谢春生等[3]提出了一种基于模糊规则系统的滚动模糊时间窗算法,对滑行路径进行动态优化。与飞机推出环节相关的研究有潘卫军等[4]基于飞机的运动学建模和(computer-aided design,CAD)二次开发,对飞机后推过程中飞机翼尖的安全间距进行了实时量化。张亚平等[5]提出一种基于停机位等待惩罚的推出控制策略,将航班滑行道等待时间转化为机位等待时间,减少了燃油消耗。Jiang等[6]建立了跑道、滑行道、停机坪的元胞传输模型,分析了场面交通演变规律,探究了飞机在不同的推出率下对机场场面交通的影响。Coupe等[7]使用机器人模拟实验模拟飞机推出和滑行至移交点的过程,分析了此过程中飞机之间的轨迹冲突,探究了冲突概率与推出时刻的关系。Lian等[8]提出了一种基于预测飞机滑行时间的动态推出控制(pushdown control flow analysis,PDPC)方法,分析滑行道排队长度阈值,通过动态调整飞机的推出时刻,提高了滑行道使用率。Bubalo等[9]开发了一种基于(large neighborhood search,LNS)算法的定位方法,对出港航班的备选顺序进行评估,找到总排放量和延误最少的航班推出顺序。何庶等[10]构建了侧向跑道航空器滑行路径优化模型,通过动态优化航班优先级。Ali等[11]使用深度强化学习(deep reinforcement learning,DRL)预测空域接收出港飞机的能力和出港飞机滑行道运行时间,回推飞机最优推出时刻,提高了机场地面运行效率。
纵观中外研究成果,在场面运行优化领域,工作集中在航班优化排序、滑行路径优化、滑行时间预测、航班推出率优化等方面,鲜有针对U型机坪区的研究,而存在U型机坪区域的机场在民用机场中占比较高,且运行环境复杂,运行效率较低,因此,提高U型区运行效率,对于缓解场面运行瓶颈问题起到关键作用。基于上述考虑,现聚焦场面关键区域,针对大型机场内的单通道U型机坪区的飞机推出等待点进行优化研究,推出等待点一般是推出线与滑行通道的切点。
1 推出等待点设计方案
1.1 传统推出等待点运行特征分析
飞机离港地面运行过程主要分为3个阶段:机坪运行阶段、滑行道运行阶段、跑道运行阶段。对于传统单通道U型区机坪运行阶段,首先是由牵引车沿着推出线顶推停机位内飞机,直至飞机鼻轮落在推出传统等待点上(传统推出等待点设置在靠近滑行道的飞机推出线端点,等待点垂直于推出线方向,推出等待点为飞机鼻轮的停止点[12]),顶推过程到此结束;顶推过程结束后飞机需要在等待点等待开始滑行指令,收到塔台允许滑行指令后,飞机由自身动力沿滑行通道滑至机坪移交点,至此机坪运行阶段结束。此过程中,牵引车将飞机顶推至传统等待点即服务结束,等待点位置固化。
对于单通道U型区出港航班,这种固化的运行方式会产生两种冲突,一种是对位飞机推出冲突,即通道两侧相对机位的飞机因机位推出时间相同或相近而导致的冲突,如图1中A、B飞机;另一种是滑行通道占用冲突,即已推出完成并开始滑行的飞机与通道两侧其他机位上、即将推出的离港飞机之间的冲突,如图1中D、C飞机位置情况。上述冲突随着航班量的增加,将可能对U型机坪区运行安全产生影响。动态配置单通道U型机坪区域的等待点,有望提高此类机坪的运行效率,正是研究的出发点。
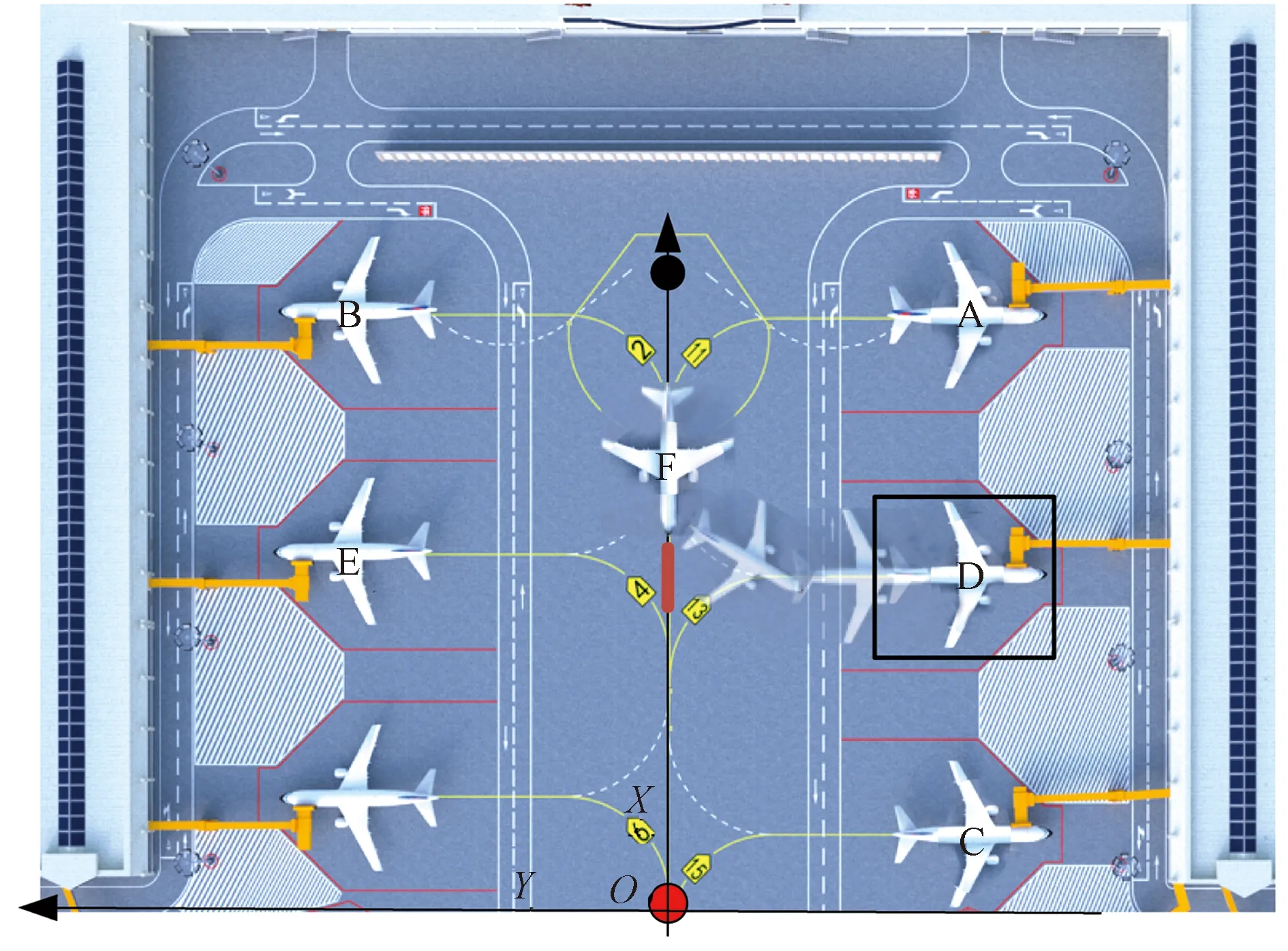
图1 推出方式示意图Fig.1 Diagram of push-back method
1.2 优化推出等待点设计基本思路
不同于传统固定式推出等待点,优化推出等待点设计思路为,根据航班计划及实时运行状况来动态设置等待点位置,且等待点的备选位置可在U型机坪内滑行通道上的任一位置点(也即不再局限于机位推出线与滑行通道的交点)。主要考虑因素为航班所在机位之间的相对位置关系以及机坪运行安全距离约束。因此,在使用优化等待点的过程中,航班的离位过程可能包括牵引车顶推至航班所在机位推出线与滑行通道的交点、牵引车拖拽航班至新的推出等待点,或两者先后组合。通过这种设计,基于航班计划,将静态等待点转化为动态等待点,可提高U型区运行效率。
以图1中A、E飞机为例具体说明上述优化思路。假设根据给定航班计划,A飞机先于E飞机推出,那么按照传统运行方式,E飞机只能在机位等待A飞机推出结束,收到滑行指令,并且滑过E飞机所在机位安全距离才能开始推出。如果两架飞机的计划推出时间间隔较小,那么E飞机会迟于计划推出时间推出,即产生了机位延误,降低了运行效率;假设计算所得飞机A的优化等待点为图1中红色点位,A飞机由牵引车顶推至传统等待点位后(图1中鼻轮黑色点位),立刻再由牵引车将A飞机向前牵引直至鼻轮落在新等待点上(图1中红色点位)。那么即使两架飞机的计划推出时间间隔较小,也不会对E飞机推出产生影响,E飞机可以按照计划时间推出。
2 优化推出等待点数学模型及算法设计
2.1 优化推出等待点数学模型
模型假设如下。
(1)每架飞机到达优化等待点后等待开车的时长固定。
(2)飞机推至传统等待点耗时相同。
(3)飞机在滑行通道内滑行的速度固定且不发生滑行偏移。
(4)不考虑进入U型区飞机的影响。
以U型区指定点位作为零点,滑行通道为X轴,建立平面直角坐标系(如图1所示)。每一架飞机滑出U型区总耗时由三部分组成,第一部分是牵引车顶推和牵引飞机到达优化等待点所耗时间;第二部分是到达优化等待点等待开车指令所耗时间;第三部分是机长收到开车指令后滑行至U型区指定点所耗时间。
则目标函数可表示为

(1)
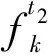
航班计划中第一架飞机实际推出时间为

(2)
两个优化等待点需要满足安全间距为
xk-xk-1>S,k≥2
(3)
式(3)中:S为等待点间最小安全间距。
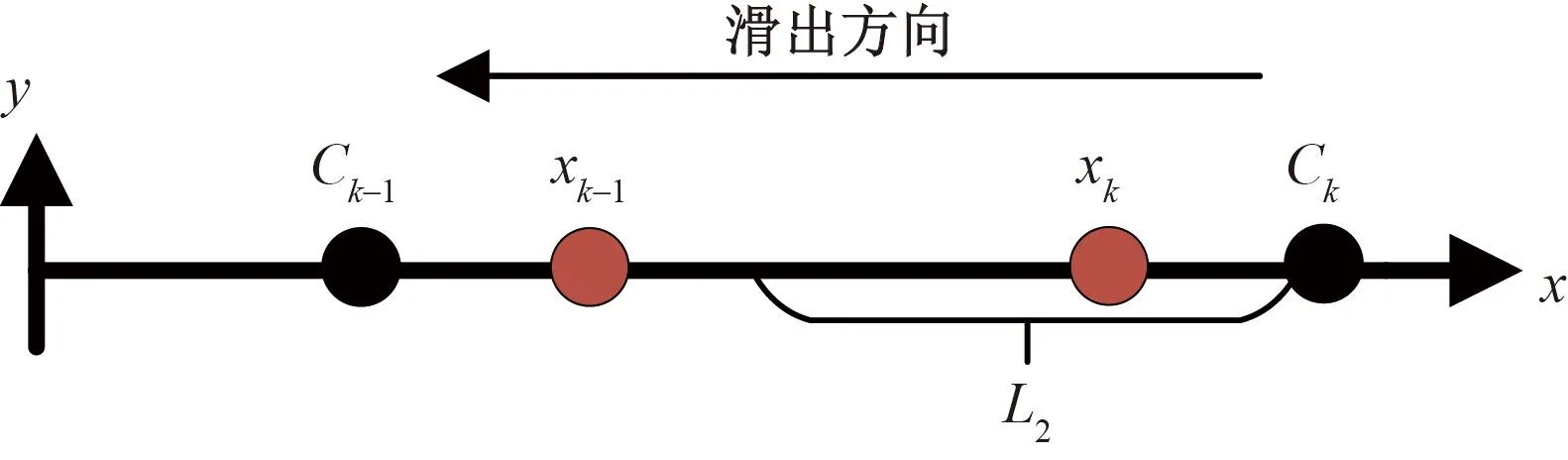
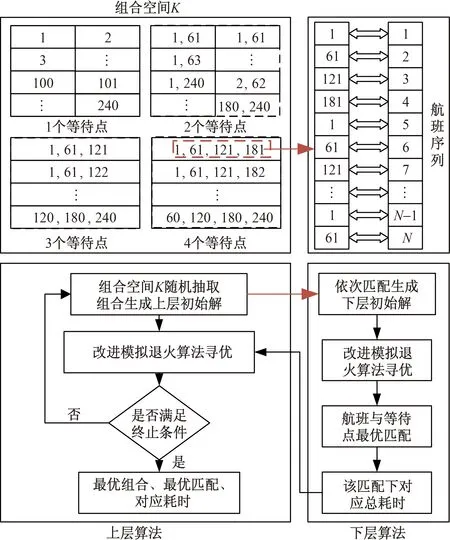
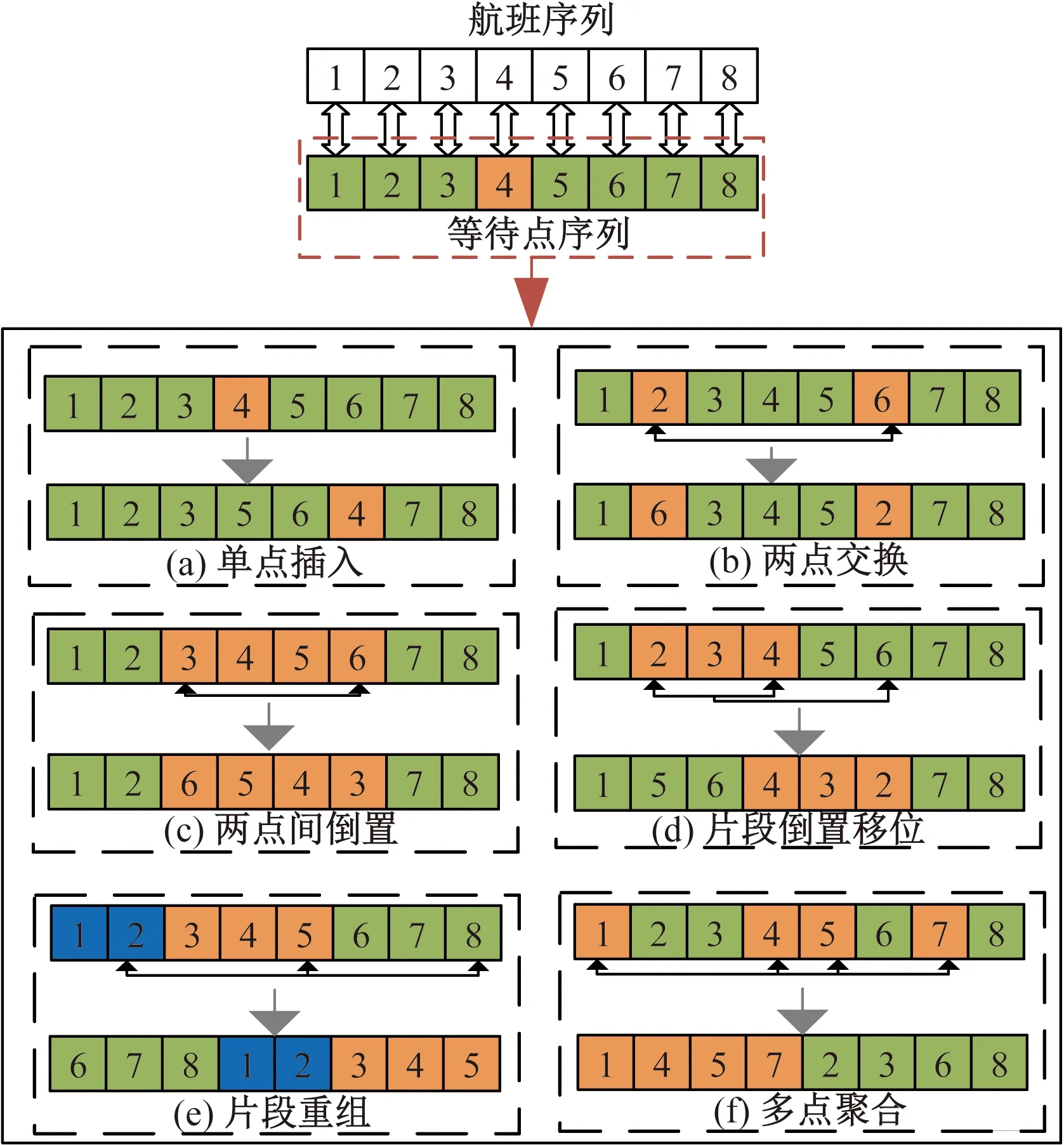
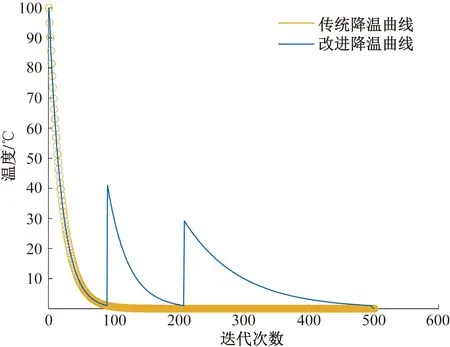
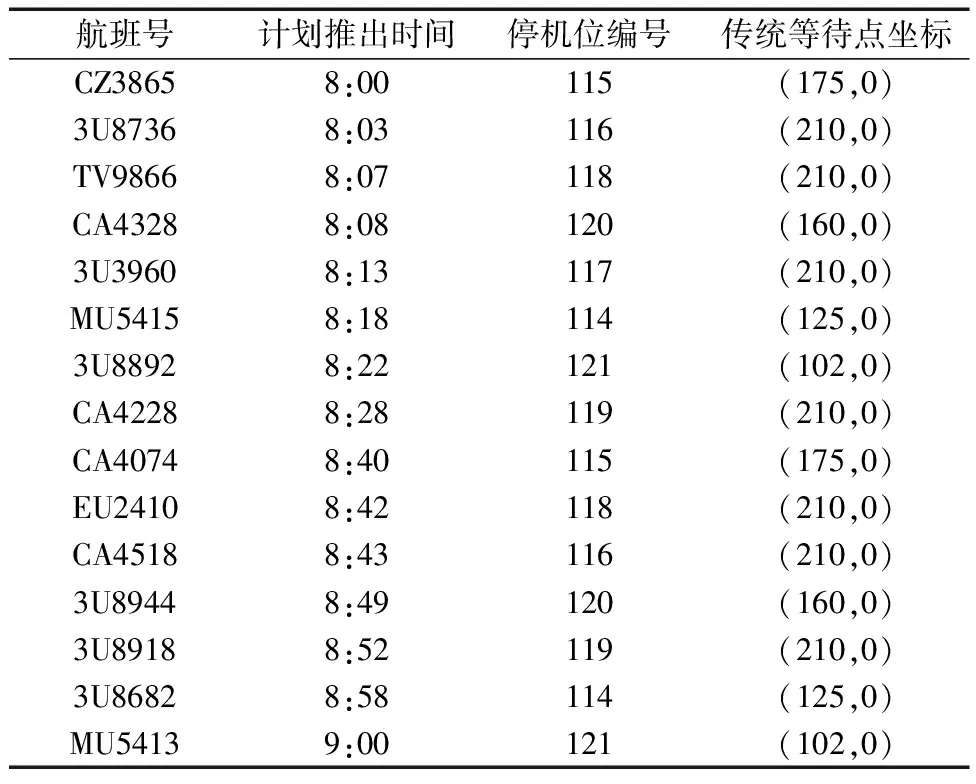
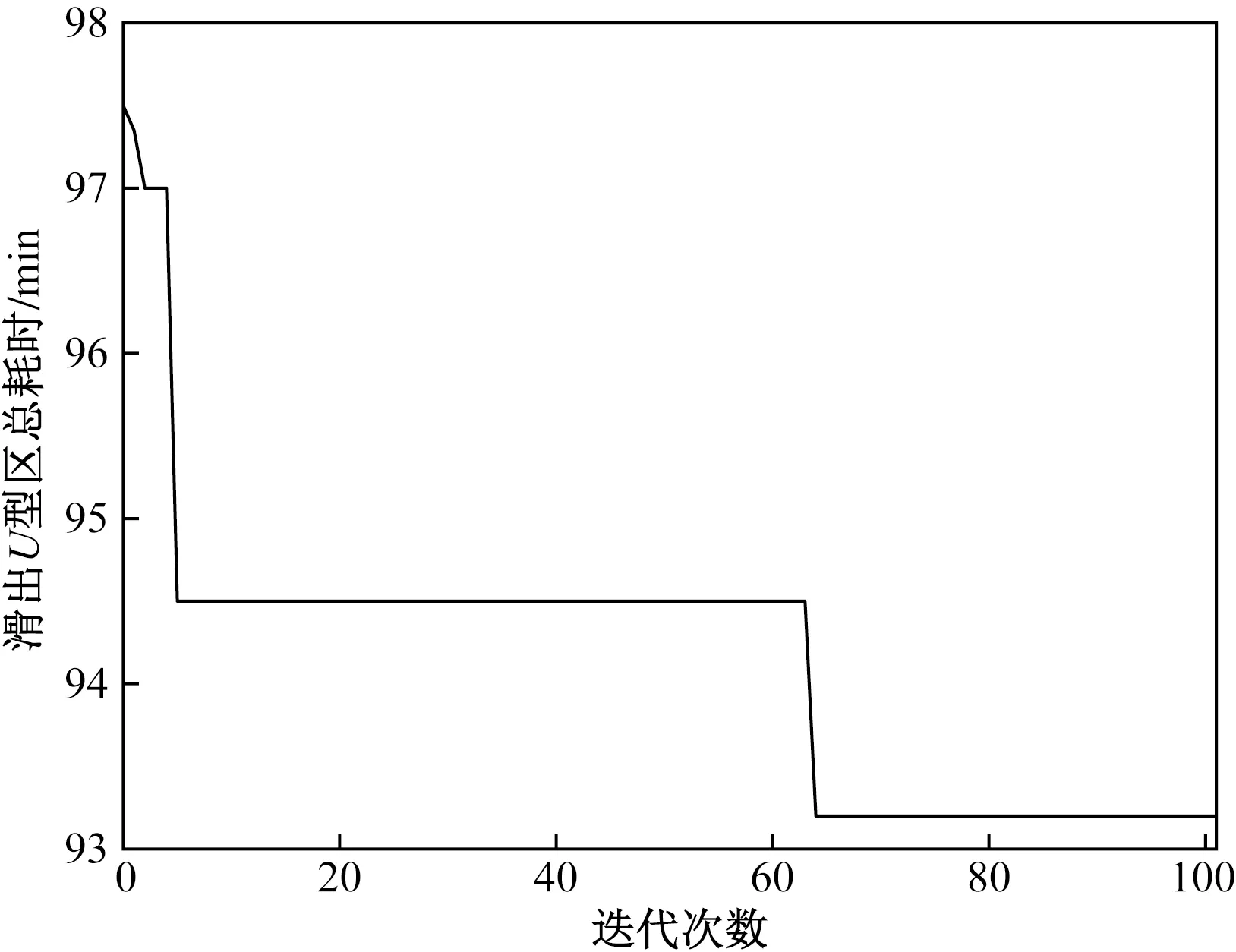
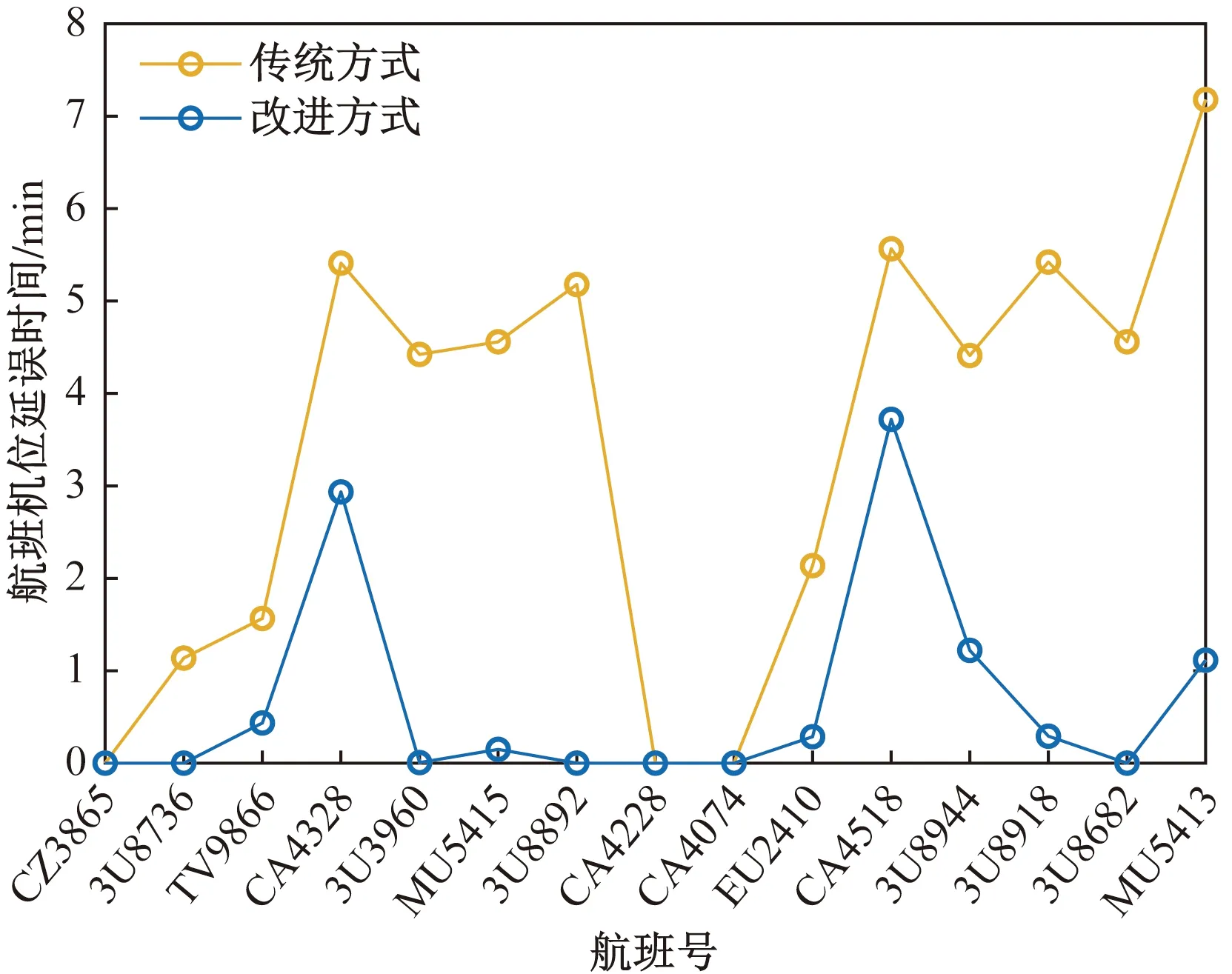
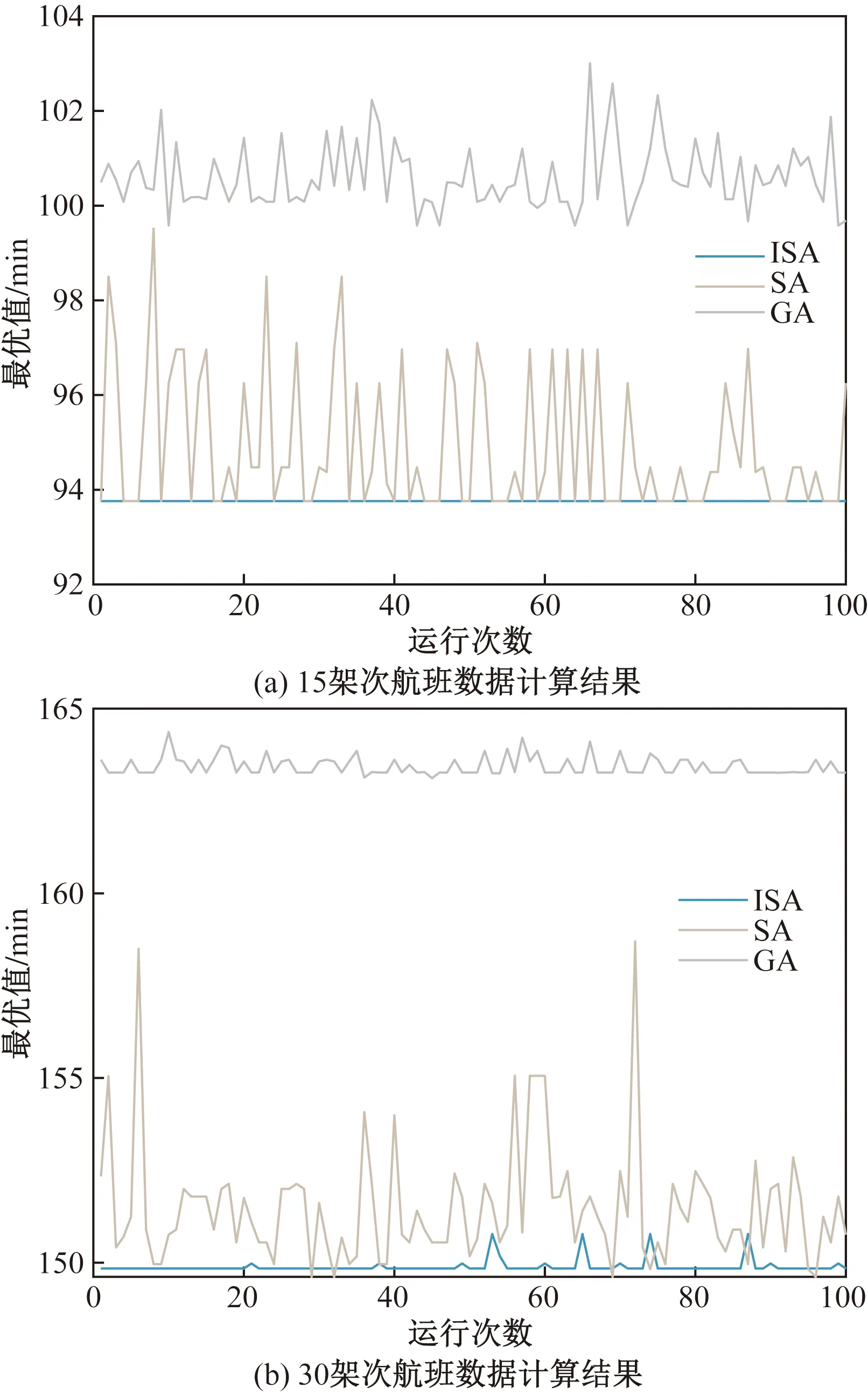
情形1前序飞机优化等待点较后序飞机传统等待点更靠近U型区底部,即Ck 图2 情形1所对应前后飞机推出等待点相对位置关系Fig.2 Relative position of aircraft push-back spot before and after scenario 1 (4) 式(4)中:L2为根据飞机推出翼尖净距要求,航班计划中前序飞机需要滑过后序飞机传统等待点的安全距离。 情形2后序飞机传统等待点较前序飞机优化等待点更靠近U型区底部,且距离不满足安全间距。即0≤Ck-xk-1≤L2,如图3所示。 图3 情形2所对应前后飞机推出等待点相对位置关系Fig.3 Relative position of aircraft push-back spot before and after scenario 2 (5) 情形3后序飞机传统等待点较前序飞机优化等待点更靠近U型区底部,且距离大于安全间距,且前序飞机优化等待点较后序飞机优化等待点更靠近U型区底部。即L2 图4 情形3所对应前后飞机推出等待点相对位置关系Fig.4 Relative position of aircraft push-back spot before and after scenario 3 (6) 情形4后序飞机传统等待点较前序飞机优化等待点更靠近U型区底部,且距离大于安全间距,且后序飞机优化等待点较前序飞机优化等待点更靠近U型区底部;同时,后序飞机传统等待点较前序飞机传统等待点更靠近U型区底部,且距离大于安全间距。即L2 图5 情形4所对应前后飞机推出等待点相对位置关系Fig.5 Relative position of aircraft push-back spot before and after scenario 4 (7) 情形5后序飞机传统等待点较前序飞机优化等待点更靠近U型区底部,且距离大于安全间距,且后序飞机优化等待点较前序飞机更靠近U型区底部;同时,后序飞机传统等待点较前序飞机传统等待点更靠近U型区底部,且距离小于或等于安全间距。即L2 图6 情形5所对应前后飞机推出等待点相对位置关系Fig.6 Relative position of aircraft push-back spot before and after scenario 5 (8) 2.2.1 算法设计基本思路 模拟退火算法(simulated annealing algorithm,SA)源于金属热处理过程中固体退火原理,对于组合优化问题有较好的求解效果[13]。 根据航班计划计算每架航班的最优等待点位置。为了达到计算目的,将目标问题拆解为两个子问题,一是求解最优等待点组合;二是求解该最优组合下与N个航班的最优匹配,两个子问题是具有上下层关系的组合优化问题。基于此,提出双层改进模拟退火算法进行计算。上层采用改进模拟退火算法,输入等待点组合给下层;下层采用改进模拟退火算法,以上层输入等待点组合为基础,模型目标函数作为评价函数,寻优结果反馈给上层,直至上层算法迭代结束。即将目标函数作为下层评价函数,将下层算法整体作为上层算法的评价函数。 2.2.2 双层算法具体流程 首先,结合单通道U型区滑行通道的长度、等待点间的最小安全间隔、需求解的精度,生成待选等待点组合空间K,等待点位置用横坐标表示。具体的生成方式如下。 (1)假设航班计划中N个航班均使用同一个等待点,对应若干可能的优化等待点。 (2)假设航班计划中N个航班使用两个不同等待点,对应若干两两等待点组合。 (3)以此类推,直至滑行通道上能够设置的最大数量等待点个数为止。将所有可能的组合存入组合空间K中。 其次,从组合空间K中随机抽取一个组合,输入给下层,将组合元素与航班序列依次匹配作为下层算法初始解,以模型目标函数作为下层算法的评价函数,输出最优匹配,以及该匹配下全部航班滑出U型区总耗时,将总耗时反馈给上层,作为上层算法每次迭代评价函数值,上层算法迭代结束输出最优等待点组合、与航班最优匹配、和对应滑出U型区总耗时,达到计算目的。以滑行通道长度280 m,等待点间隔60 m,需求解精度1 m,其过程与双层算法流程如图7所示。 图7 双层算法结构示意图Fig.7 Schematic diagram of two-layer algorithm structure 2.2.3 上下层算法改进方式 传统模拟退火算法基本步骤如下。 步骤1参数初始化,初始温度T0,令当前温度T=T0,生成初始解K1,计算评价函数值f(K1)。 步骤2对当前解K1进行扰动,产生新解K2,计算评价函数值f(K2)。 步骤3计算评价函数值增量ΔE=f(K2)-f(K1)。若ΔE<0,则接受新解K2为当前解;否则,计算p=exp(-ΔE/T)值,再生成(0,1)均匀分布随机数r,若p>r,则接受K2为当前解,否则不接受,即Mtropolis准则。 步骤4判断在当前温度是否充分搜索,是则降温重复步骤2,否则在当前温度下重复步骤2。 步骤5判断是否满足终止条件,满足则输出当前解,否则重复步骤2。 传统模拟退火算法流程图如图8所示。 图8 传统模拟退火算法流程图Fig.8 Flow chart of traditional simulated annealing algorithm 许多学者对传统模拟退火算法进行了改进,李建国等[14]提出了一种带有记忆功能的模拟退火算法,提高了解的质量;李朝迁等[15]将遗传算法与模拟退火算法融合,使用混合生成初始解的方式,提高初始解质量;王旭等[16]利用贝叶斯优化,实现模拟退火算法自动调参。针对组合空间K以及等待点匹配特征,对于上层模拟退火算法,设计变降温系数的重回温操作;对于下层模拟退火算法,设计多邻域并行搜索产生新解。以此提高解的质量以及满足管制员决策实时性要求。 步骤1上下层算法编码方式与初始解。对于上层算法,对组合空间K中的组合编号,从1开始,每个编号对应上层算法中的一个解,随机抽取一个编号作为初始解;对于下层算法,将上层输入编号解译为对应等待点组合,将组合依次与航班序列匹配,作为下层算法初始解。 步骤2上层与下层生成新解。对于上层算法,结合上层解的特征,设计一种变步长的搜索方式,步长与温度相关,以契合算法的收敛特征。具体生成方式如式(9)所示。 H=H1+CT0 (9) 式(9)中:H为新解;H1为初始解;T0为当前温度;C为常数。若解超出编号范围,则重新向反方向搜索生成新解。 对于下层算法的步骤2,设计多邻域并行搜索,传统模拟退火算法对于新解的产生主要使用2-opt法,考虑等待点与航班的匹配特征,这种扰动方式产生新解的能力有限,故设计6种邻域并行搜索的策略,即单点插入、两点交换、两点间倒置、片段倒置移位、片段重组、多点聚合。使用模型目标函数对每次产生的6个新解进行计算,根据贪婪准则,选择最优新解参与下一阶段运算。此策略可以提高算法迭代后期跳出局部最优的能力。6种操作如图9所示。 图9 新解扰动示意图Fig.9 Schematic diagram of the new solution perturbation (1)单点插入:在等待点序列中随机抽取一个点插入另外一个随机位置。 (2)两点交换:在等待点序列中随机抽取两个点,相互交换位置。 (3)两点间倒置:在等待点序列中随机抽取两个点,完全颠倒两点及其之间的序列 (4)片段倒置移位:在等待点序列中随机抽取3个点,将前两点及其之间的序列颠倒后插入第3个随机点后。 (5)片段重组:在等待点序列中随机抽⎣N/2」个点,将等待点序列分成⎣N/2」个片段再将片段随机重组。 (6)多点聚合:在等待点序列中随机抽⎣N/2」个点,将其按顺序排列前置,其于按顺序排列后置。 步骤3重升温操作。对于上层算法的步骤4,当温度低于一定值时,根据Mtropolis准则特征可知,算法对新解的接受概率接近于0,此时算法跳出局部最优概率接近于0,为了使算法保持跳出局部最优能力,设计变降温系数的重升温环节。重升温公式如式(10)所示。 (10) 式(10)中:T为当前温度;T0为初始温度;maxgen为外循环迭代次数;iter为该温度下对应的迭代次数;c、c1均为常数;α为降温系数。图10为改进降温函数的降温曲线与相同参数下的传统降温曲线。 图10 降温曲线Fig.10 Cooling curve 步骤4结果输出。上层算法迭代结束即整体算法迭代结束,输出最优等待点组合、与航班最优匹配、和对应滑出U型区总耗时,即得出航班计划中每架航班的优化等待点位置与对应的滑出U型区总时间。 以某大型机场B、C指廊之间的U型区为背景,选取U型区早高峰时段8:00—9:00的离场航班数据,如表1所示。该区域有8个停机位,滑行通道总长度260 m,简图如图11所示,以滑行通道为x轴,与滑行通道停止线交点为坐标原点,滑行通道停止线延长线为y轴建立平面直角坐标系。根据A320的机型数据,结合文献[4]的计算方式,L2为60 m。飞机后推距离L1为135 m,后推速度设70 m/min,前滑速度120 m/min。两等待点间最小间距60 m, 设置每架飞机到达优化等待点后等待开车的时长Tw为2 min。设置等待点精度为1 m。 表1 航班计划表 图11 双流机场单通道U型区构型图Fig.11 Shuangliu Airport single-aisle U-shaped area configuration 经反复试验,对算法的各参数设置如下:对于下层算法,初始温度T0=100,最大迭代次数maxgen=200,Markov链长lk=10,降温速率α=0.9;对于上层算法,初始温度T0=1 000,最大迭代次数maxgen=100,Markov链长lk=5,降温速率α=0.9,升温阈值c=1,变降温速率参数c1=1.02。 所得结果为,滑出U型区总耗时93.2 min,对应航班计划中各航班最优等待点位置如表2所示。迭代过程如图12所示,可见算法在后期陷入局部最优,通过回温操作搜索到更优值。 表2 优化等待点位计算结果 图12 迭代过程Fig.12 Iterative process 与优化前的推出方式进行对比。优化前,航班计划中各飞机滑出U型区总耗时为132.1 min。使用表2所示优化点位,15架航班总出港时间从132.1 min 降低到93.2 min,减少了29.4%。机位延误总时间从51.55 min降低到10.35 min,降低了79.9%。计耗时34 s,满足决策需要。即使航班计划临时调整,也能在允许的时间范围内重新计算优化等待点位置。若不设计双层算法结构,使用单层算法对组合空间K进行遍历计算,所得解为92.5 min,虽然结果较优,但其耗时为52 887.24 s,可见双层改进模拟退火算法的设计在保证解质量的前提下使得计算时间大幅缩短。为了直观体现优化效果,将优化对比结果绘制如图13所示,各航班机位延误时间如图14所示。 图13 机位总延误与滑出U型区总耗时Fig.13 Total delay time for parking space and total time for taxiing out of U-shaped area 图14 各航班机位延误Fig.14 Length of delay in parking space per flight 根据所设计算法的结构特征,验证顺序从下层至上层,使用算例中的U型区,分别输入15架次航班数据和某时段30架次航班数据并进行多次计算。 首先进行下层算法有效性验证,从组合空间K中随机抽取一个序号作为下层算法的输入,所抽编号解译的等待点组合为(29,89,149,210),将下层设计的改进模拟退火算法(improved simulated annealing algorithm,ISA)与模拟退火算法(SA),遗传算法(genetic algorithm,GA)进行对比。ISA与SA所设参数与上述算例相同,GA与ISA运行时间相同。每种算法独立运行100次,运行结果如图15所示。 图15 下层算法稳定性对比Fig.15 Comparison of the stability of lower-level algorithms 模拟退火算法是一种随机搜索算法,在同一初始解的情况下,所得解具有随机性。由于下层算法需频繁调用,因此下层算法求解稳定性和求解质量与整体算法的性能直接相关。如图15所示,通过多邻域搜索产生新解,使ISA算法解的稳定性和质量均高于其他两种算法。 其次进行上层算法有效性验证,将上层设计的改进模拟退火算法(ISA)与模拟退火算法(SA),差分进化算法(differential evolution,DE)进行对比。3种上层算法所调用的下层算法均为改进的模拟退火算法,下层算法参数设置与上述算例相同。上层ISA与SA所用参数与上述算例中参数相同,DE运行时间与ISA相同。每种算法独立运行100次,每种上层算法在不同数据量输入下,100次运行的平均值、最小值、最大值如图16所示。 图16 上层算法结果对比Fig.16 Comparison of upper-layer algorithm results 下层算法与上层算法构成所设计的双层改进模拟退火算法结构,验证上层算法性能即为验证整体算法性能。由图15可知,通过对上层算法增加回温操作,使求解的平均值、最小值、最大值均优于其他两种算法。最大值与最小值反映算法寻优能力,平均值反映算法寻优平均状态[17]。与优化前相比,30架次航班滑出U型区总耗时仍可以节约14.8%,且100次计算的平均时间为40 s,满足决策需要。因此,双层改进模拟退火算法比其他两种算法性能更优,且能满足U型区高峰时段不同规模出港航班的计算需求。 (1)改变了大型机场单通道U型区原有的推出方式,设计了基于高峰时段航班计划的动态等待点,使航班计划内飞机滑出U型区总耗时降低29.4%,机位延误总时间降低了79.9%。 (2)设计了一种双层模拟退火算法结构,并分别对上下层算法进行改进,对于上层算法,设计了基于温度阈值的变降温系数重升温操作;对于下层算法,改进了新解扰动方式。相比于其他算法,解的质量和求解稳定性更优,且求解时间满足决策要求。 (3)下一步工作是加入进港航班对出港的影响,制定等待点精度选择标准,做多通道U型区推出等待点研究。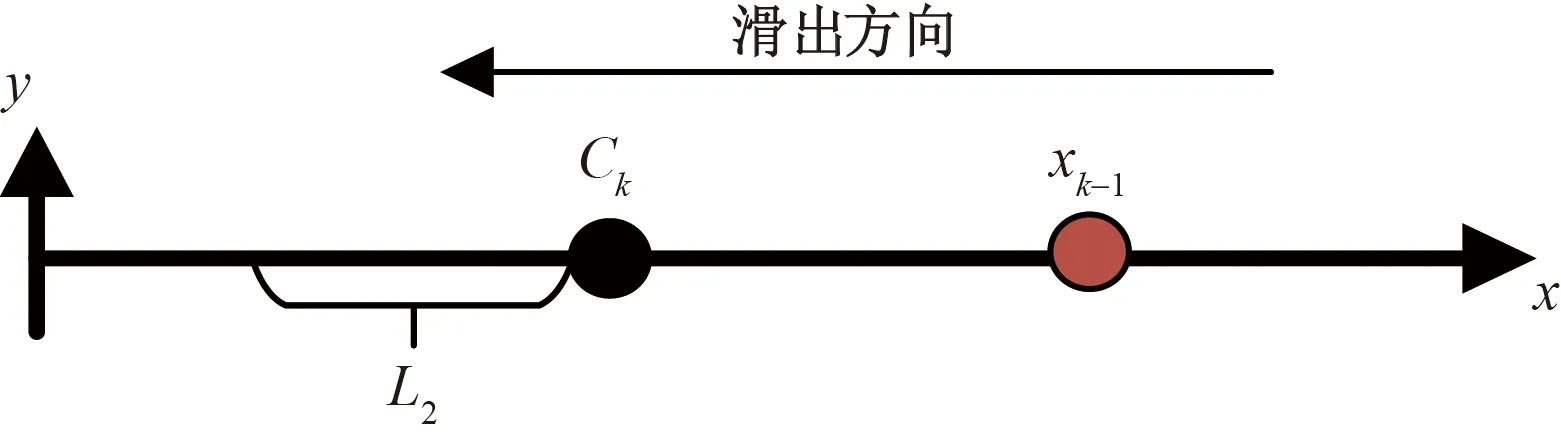
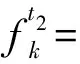


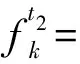





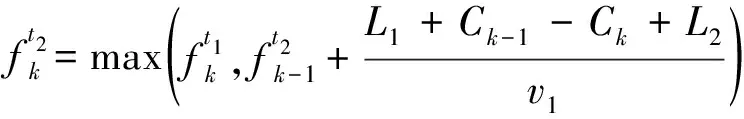
2.2 双层改进模拟退火算法设计


3 算例验证
3.1 算例设计


3.2 优化效果分析

3.3 双层改进模拟退火算法有效性分析

4 结论
