改进的粒子群优化算法在云计算任务调度中的应用
2023-11-04汪婷邵鹏李光泉刘珊慧
汪婷, 邵鹏, 李光泉, 刘珊慧
(江西农业大学计算机与信息工程学院, 南昌 330045)
云计算(cloud computing,CC)是以互联网为核心,根据用户需求,动态存储、整合相关资源,向用户提供高性能服务的一种新兴技术。调度技术作为云计算的关键技术,能够对物理资源进行高效管理,以获得更好的资源配置方案。Bisht等[1]综合考虑异构环境下的成本、最大完成时间等因素,提出改进Min-Min工作调度算法。Alworafi等[2]基于最短作业优先,以最小化任务完成时间和平均响应时间为目标提出改进算法,同时最大化资源利用率。Alhuidari等[3]利用轮询算法,根据时间量子平均值自适应更新,提高云计算系统吞吐量。然而,传统的先来先服务、短作业优先等确定性调度算法因时间开销大,可靠性低,通常无法获得最佳调度方案。
现有方法表明,启发式算法可通过预测获得时间复杂度低的近似最优解[4]。Liu等[5]针对云计算任务调度中普遍存在的资源利用率低这一缺点,提出基于不同信息颗粒的贪心调度策略,并针对不同特征的任务分配不同的调度策略。由于处理任务的成本和能耗较高,启发式算法不适用于处理云计算任务调度问题。而元启发式算法能够在不预先告知任务和资源的条件下直接获得最优解,且结果优于启发式算法,因此被广泛用于求解云计算任务调度问题,包括鲸鱼优化算法[6]、遗传算法[7-9]、人工蜂群算法[10-11]以及粒子群优化算法[12-14](particle swarm optimization,PSO)等。其中,PSO算法是Kennedy和Eberhart于1995年提出的基于群体协作的随机搜索算法,具有原理简单、收敛速度快等特点,被认为是求解云计算任务调度问题最具潜力的方法之一。
从已有的研究成果中可以发现,传统PSO算法在求解云计算任务调度问题中存在收敛速度慢、精度低等缺陷[15]。Dubey等[16]受化学反应优化算法启发,通过迭代算子保存具有高适应度值的次优解,并用于下一次迭代,以提高PSO算法解的质量,加快粒子收敛速度。张思豪等[17]引入资源状态指标,分批处理任务寻求最优解,缩短任务完工时间。Nanjappan等[18]通过冠状模糊均值算法对独立任务进行聚类并调度至各虚拟机中执行,最后通过PSO算法计算特征值,有效提高结果精度。马学森等[19]提出一种多策略融合的改进PSO算法,首先引入非线性惯性权重策略提高粒子寻优能力,接着通过花朵授粉算法平衡算法的探索与开发,最后利用萤火虫算法产生“精英解”对粒子位置进行扰动,跳出局部收敛,改进算法在收敛速度和精度上都获得明显提升,但存在寻优效率低等问题。因此孙长亚等[20]利用动态更新惯性权重策略提高PSO算法的自适应搜索能力,同时引入微生物遗传算法,在算法前期缩小目标搜索空间,并在算法后期利用PSO算法快速收敛,获得全局最优解,提高算法寻优效率。
此外,为降低算法陷入局部极值的概率,Nabi等[21]基于线性递减自适应惯性权重策略提出一种自适应粒子群优化算法,以平衡算法的局部搜索和全局搜索能力,避免算法陷入局部极值。朱琳等[22]采用非线性递减惯性权重更新策略提高算法后期收敛能力。谭鹤毅等[23]利用天牛须搜索算法实现多个个体同步计算,提高种群间信息交互能力,帮助粒子跳出局部极值。尽管众多学者针对PSO算法在求解云计算任务调度问题中存在的收敛速度慢、精度低、易陷入局部极值等缺陷,分别开展了大量的研究工作并且提出了相应的改进算法。然而,针对PSO算法存在的以上3种缺陷进行同时改进,并将其应用于求解云计算任务调度问题,仍将是一个极富挑战的任务。
综上,针对PSO算法在求解云计算任务调度问题上的缺陷,综合考虑最大完成时间最少、任务执行总时间最优两个优化目标,在PSO算法中融合模拟退火算法[24](simulated annealing, SA)、饥饿游戏搜索[25](hungary games search,HGS)及双重变异限制策略[26](double restrictions),现提出一种融合多种策略的粒子群优化算法(multi-strategy particle swarm optimization, MSPSO)。引入模拟退火算法动态更新粒子惯性权重,平衡算法的探索和开发,避免算法陷入局部极值。引入饥饿游戏搜索算法优化粒子位置更新策略,加快粒子收敛速度,提高结果精度(更优数量级)。引入双重变异限制策略同时限制粒子速度和位置,避免粒子发生越界,提高算法寻优效率。将所提算法MSPSO应用于求解云计算任务调度问题,在不同任务量下进行对比实验,以验证MSPSO算法在实际应用中的可靠性和实用性。
1 云计算任务调度描述
云计算是一种全新的、基于并高度依赖Internet、自助式使用远程计算资源的技术,具有按需服务、动态可拓展、虚拟化等特点,它主要包括3种服务模式:基础设施即服务(IaaS)、平台即服务(PaaS)和软件即服务(SaaS)。通常在云计算环境中,一个用户任务被切分成n个不同大小、相互独立的子任务,子任务集合可以用字母N表示为:N={n1,n2,…,nn},假设所有的子任务被分配到m个虚拟机上执行,虚拟机拥有CPU、内存、存储等资源,用VM表示为:VM={vm1,vm2,…,vmm}。其中,n>m,ni(1≤i≤n)表示第i个任务,vmj(1≤j≤m)表示第j个虚拟机。任务调度即将n个子任务调配到m个虚拟机中执行,并获得最佳调度方案,实现任务执行的最大完成时间最小、任务执行总时间最优等目标。云计算任务调度的框架可简化为图1。
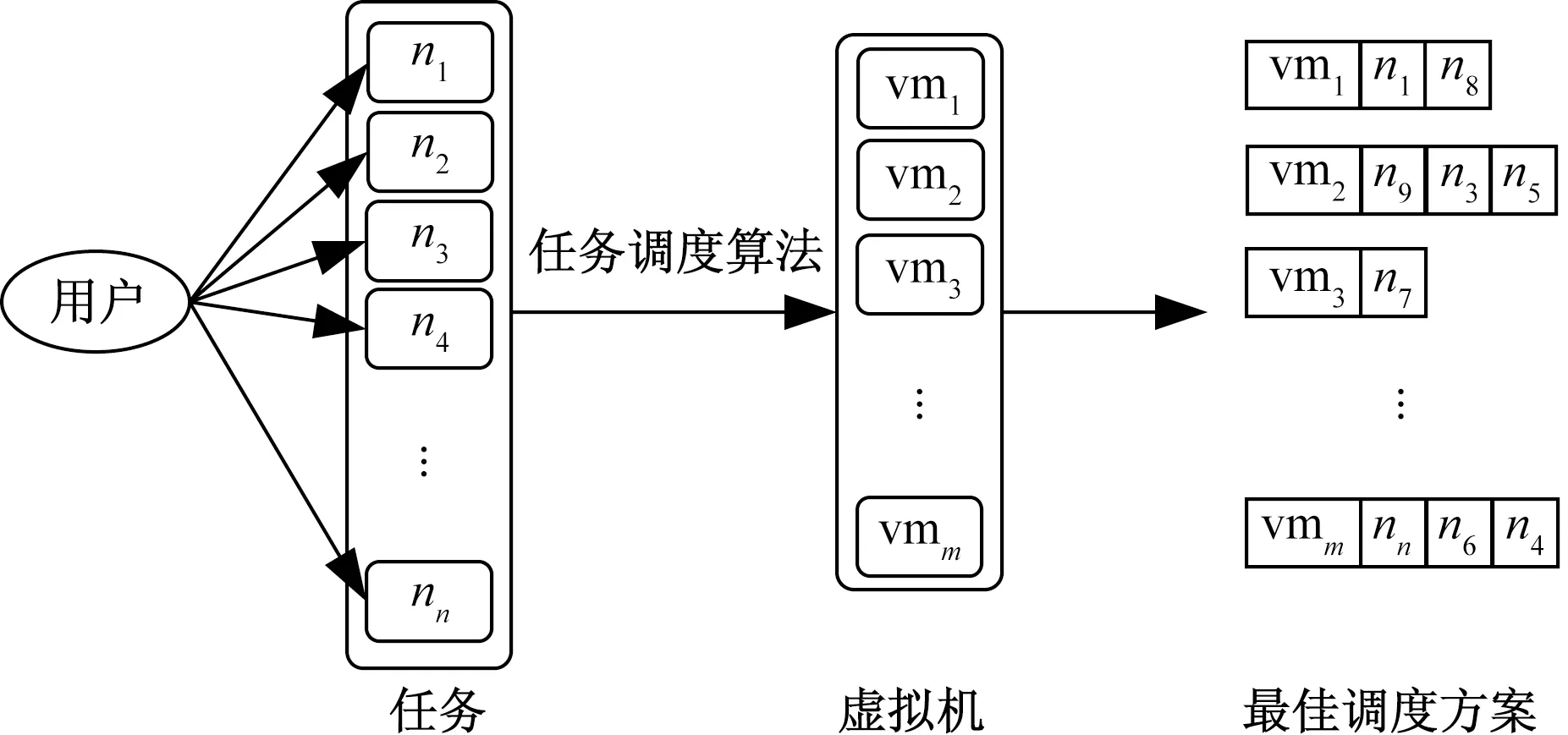
图1 云计算任务调度框架Fig.1 Cloud computing task scheduling framework
为了便于计算每个任务完成调度所需要的时间,分别定义一个n×m的矩阵E,T。其中,E为子任务在各虚拟机上的执行时间矩阵,如式(1)所示。T为将子任务数据传输到各虚拟机上的传输时间矩阵,如式(2)所示。

(1)

(2)

2 多策略融合的粒子群优化算法
2.1 粒子群优化算法
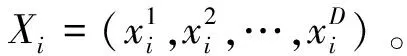
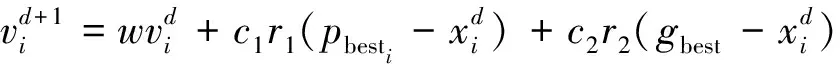
(3)

(4)

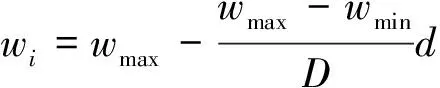
(5)
式(5)中:wmax为最大惯性权重;wmin为最小惯性权重。
2.2 改进的粒子群优化算法
为克服PSO算法在求解云计算任务调度问题中存在的早熟收敛、易陷入局部极值等缺陷,基于PSO算法,融合饥饿游戏搜索、模拟退火算法和双重变异限制策略,提出了一种多策略融合的粒子群优化算法MSPSO,运行机制如图2所示。首先使用模拟退火算法动态更新惯性权重,平衡算法的探索与开发;其次通过饥饿游戏搜索优化粒子的位置更新策略,加快粒子收敛速度,提高结果精度;最后采用双重变异限制策略防止粒子越界,提高算法寻优效率。

图2 MSPSO算法的运行机制Fig.2 The operation mechanism of MSPSO algorithm
2.2.1 惯性权重更新策略
在MSPSO中,首先随机初始化粒子的位置和速度,通过计算粒子适应度值,获得全局最佳位置gbest和局部最佳位置pbest。惯性权重w是PSO算法的重要参数之一,当w较大时,算法的全局寻优能力增强,粒子更容易跳出局部极值,但同时会降低搜索效率,不易收敛;反之亦然。模拟退火算法[24]是一种基于概率的算法,通过设置模拟退火概率P来动态调整惯性权重。若当前迭代次数t是正整数k的整数倍时,调用模拟退火算法,惯性权重更新公式为
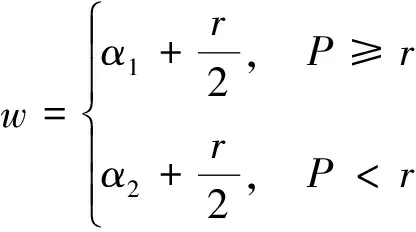
(6)
式(6)中:α1、α2为[0,1]内常数,且α1>α2;r为[0,1]内常数,模拟退火概率P公式为

(7)

2.2.2 位置更新策略
饥饿游戏搜索算法[25]受动物社会行为的影响,将个体的饥饿程度h作为个体饥饿特征进行数学模拟。将算法用于优化粒子位置更新策略,可以提高粒子间的信息交互能力,在算法后期加快粒子的收敛速度,改进后的粒子位置公式为

(8)

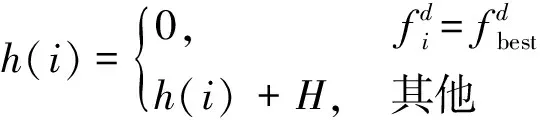
(9)
2.2.3 边界限制策略
PSO算法在搜索空间寻找最优解过程中,容易发生粒子越界。在已有研究中,大部分策略采用限定粒子位置、降低粒子飞行速度等方式限制粒子行为,然而当粒子飞出搜索空间且速度很大时,只限制粒子位置而不降低粒子速度,仍可能发生越界行为。采用双重变异限制策略[26],可同时限制粒子位置和速度,将粒子控制在搜索空间内,其限定因子χ公式为

(10)
式(10)中:φ=0.5。则χ被限制在[0,0.5]范围内,可有效解决算法由于加入过多随机性而导致的收敛速度过快和收敛精度不足的问题。
MSPSO的伪代码如表1所示。现对MSPSO的时间复杂度进行分析,标准粒子群优化算法的时间复杂度为O(M×Tmax×D),其中M为粒子总数,Tmax为最大迭代次数,D为维度。惯性权重更新策略、位置更新策略、边界限制策略为O(M×D),故MSPSO的时间复杂度约为O(M×Tmax×D)。

表1 MSPSO的伪代码
3 MSPSO算法性能对比
为验证所提算法的优越性,分别在30、50、100、1 000共4种维度下,将MSPSO算法与PSO、QUAPSO[27]、ADPSO[21]这3种算法进行对比实验,其参数设置为:粒子总数M=100、最大迭代次数Tmax=500。考虑到粒子群优化算法的随机行为,在运行100次后取平均值作为最终结果。
选取了13个基准测试函数验证所提算法的有效性,如表2所示,其中f1~f5为单模态函数,f6~f10为多模态函数,f11~f13为固定维数函数。

表2 基准函数
为了评估算法的效率和性能,分别从适应度平均值Avg、最小值Min、标准差SD 3个方面进行评估。表3为各算法在求解高维问题(D=1 000)时获得的适应度Avg、Min、SD。
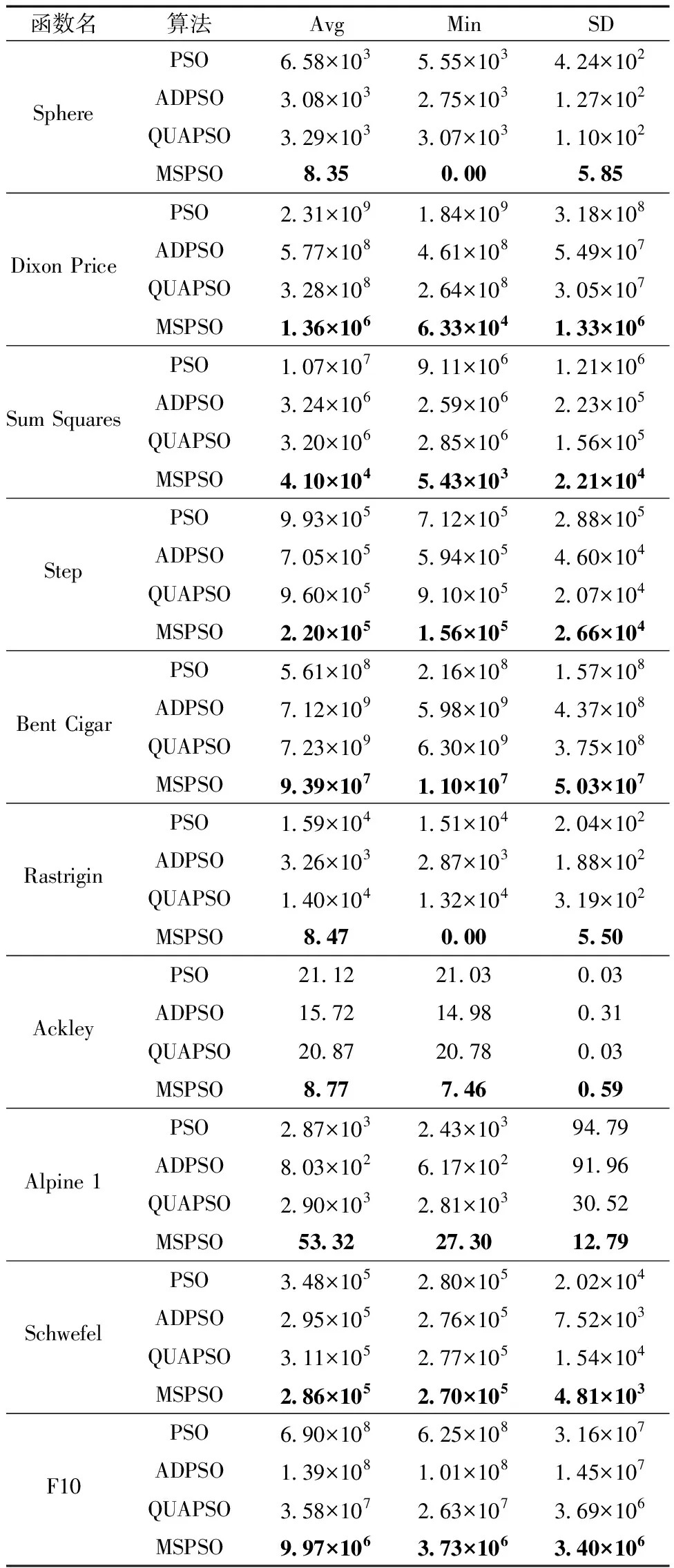
表3 各算法求解高维问题的最优值统计
如表3所示,在求解单模态问题f1~f5时,MSPSO算法相比其他算法,能够获得更优数量级的最优解。以Dixon Price函数为例,MSPSO适应度平均值分别比PSO、ADPSO、QUAPSO低99.94%、99.76%、99.58%,最小值低99.99%、99.98%、99.97%,标准差低99.58%、97.57%、95.63%。这得益于饥饿游戏搜索算法在MSPSO算法后期引导最优粒子快速靠近全局最优解,加快算法收敛速度,提高结果精度。在求解多模态问题f6~f10时,MSPSO相比其他算法,同样可以获得更优解,表明MSPSO算法中惯性权重更新策略在保持种群多样性,平衡算法的探索与开发方面效果显著。图3表示当维度D=1 000时,各算法在Sphere、Dixon Price、F10中的适应度平均值对比,可以看出MSPSO在收敛性、跳出局部极值等方面都明显优于其他算法。各算法求解低维(D为30、50、100)及固定维数问题获得的适应度Avg、Min、SD如表4所示。

表4 各算法求解低维及固定维数问题的最优值统计

图3 各算法在3个基准函数中的适应度平均值对比Fig.3 Comparison of the fitness of each algorithm in three benchmark functions
4 MSPSO用于云计算任务调度
4.1 粒子编码
PSO算法是一种解决连续问题的元启发式算法,将其应用于求解任务调度问题,首先需要构建有效的粒子编码方案。采用间接编码方式,设粒子位置编码长度为子任务个数,一个子任务对应一个虚拟机。举例说明,若子任务数N=10,虚拟机数VM=5,则粒子i的位置编码长度为10,可以表示为xi={2,4,5,1,3,4,2,5,1,4},其第1位编码表示子任务n1在虚拟机vm2上执行,第2位编码表示子任务n2在虚拟机vm4上执行,依此类推。其映射关系如表5所示。

表5 子任务与虚拟机间映射关系
4.2 适应度函数设计
综合考虑最大完成时间最小、任务执行总时间最优两个优化目标,MSPSO的数学模型描述如下。
定义1任务执行总时间。
任务执行总时间Tsum指按调度方案,各虚拟机完成其分配子任务的总时间,Tj表示虚拟机VMj完成分配子任务的总时间,公式如下。

(11)
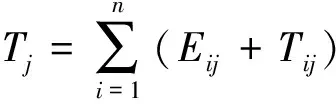
(12)
定义2最大完成时间。
任务的最大完成时间Tmax表示最后一个子任务的完成时间,公式为
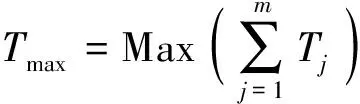
(13)
适应度函数由式(14)获得。
Fitness=αTsum+(1-α)Tmax
(14)
式(14)中:α为优化目标对适应度函数的影响权重。将云计算任务调度问题转变为找到适应度最小值的任务调度方案。
4.3 任务调度流程
融合多策略粒子群优化算法的云计算任务调度部署流程如下。
步骤1初始化云计算数据中心的物理主机列表和虚拟机列表。
步骤2初始化算法参数,设置惯性权重w、最大迭代次数Tmax、常数l等。
步骤3粒子编码,初始化粒子位置和速度。
步骤4迭代次数t=t+1。
步骤5根据式(14)计算粒子适应度值,更新gbest和pbest。
步骤6维度d=d+1。
步骤7判断当前迭代次数t是否为正整数k的整数倍,若是,则调用随机惯性权重策略根据式(6)动态更新惯性权重w,否则根据式(5)更新。
步骤8根据式(3)更新粒子速度。
步骤9判断当前维度d是否为整数z的整数倍,若是,则调用饥饿游戏搜索算法,根据式(8)更新粒子位置;否则调用式(4)。
步骤10更新后,粒子的编码序列范围可能超出设定阈值,此时调用双重变异限制策略,同时限定粒子位置和速度,防止粒子发生越界。
步骤11若当前维度d 步骤12若当前迭代次数t 使用Cloudsim模拟云计算环境,包括数据中心、物理主机、虚拟机及云服务代理等。实验环境:Eclipse Kepler Release、Intel(R) Core(TM) i5-7200U CPU @ 2.50 GHz 2.71 GHz处理器,4 GB内存。实验环境的配置如表6所示。 表6 实验环境配置 为确保实验结果的公平性,所有算法的参数设置都相同:种群规模为25,最大迭代次数为2 000,任务数分别设置为40、60、80和100,实验结果在算法运行100次后取平均值作为最终结果。详细参数设置如表7所示。 表7 参数设置 任务调度的性能指标由总成本C来衡量,即各子任务在虚拟机上的执行时间Eij与云计算资源中任务的执行成本c的乘积之和。其计算公式为 (15) 为验证MSPSO在求解云计算任务调度问题中的有效性,分别从适应度值、总成本两个角度,将所提算法MSPSO与LWPSO[28]、GWOPSO[29]及EEAPSO[30]3种改进粒子群优化算法进行比较。 为测试本文算法在总成本上的优劣,分别将MSPSO与LWPSO、GWOPSO、EEAPSO在任务数为40、60、80、100的条件进行实验对比,对比结果如图4所示。可以看出,对于所有测试用例,MSPSO的总成本均远低于其他3种对比算法。这是因为MSPSO中引入了饥饿游戏搜索算法,通过粒子的“饥饿程度”(它们对寻找最优解的影响)动态选择位置更新策略,可以提高粒子间信息交互能力,加快粒子收敛速度。同时,引入双重变异限制策略提高了算法寻优效率,有效降低任务执行时间,实现总成本最小化。当任务数为40时,MSPSO总成本比LWPSO、GWOPSO、EEAPSO低14.4%、15.3%、11.2%。随着任务数逐渐增多,各算法的总成本差额有所减小,当任务达到100时,MSPSO总成本比LWPSO、GWOPSO、EEAPSO低13.5%、12.8%、10.6%。 图4 不同算法在不同任务量下的成本比较Fig.4 Cost comparison of different algorithms for different task volumes 此外,综合考虑最大完成时间最少、任务执行总时间最优两个目标,将寻找最佳调度方案问题转化为寻找适应度最小值问题。通过比较MSPSO与其他3种算法在适应度值方面的表现来进一步评价算法性能,在不同任务量下的对比实验结果如图5所示。对于所有测试用例,MSPSO的适应度值均远低于其他对比算法,且随着迭代次数的增加,MSPSO与其他对比算法的适应度差值逐渐增加,验证了MSPSO在求解云计算任务调度问题中的有效性。原因在于算法中引入了模拟退火算法,在调度过程中动态更新粒子惯性权重,有效平衡了算法的全局搜索和局部搜索能力,避免粒子在算法后期陷入局部极值。在图5 (a)中,MSPSO的适应度值分别比LWPSO、GWOPSO、EEAPSO低10.5%、10.6%、7.6%。随着任务数逐渐增多,各算法间的适应度差值有所减小。在图5 (d)中,MSPSO的适应度值分别比LWPSO、GWOPSO、EEAPSO低9.9%、8.3%、6.5%。 图5 不同算法在不同任务量下的适应度值比较Fig.5 Comparison of fitness values of different algorithms under different tasks 综合以上分析,MSPSO相比其他3种对比算法,在适应度值、总成本两个方面均表现出明显优势,适用于求解云计算任务调度问题。 针对粒子群优化算法在求解云计算任务调度问题中存在的不足,提出一种新的融合模拟退火算法、饥饿游戏搜索和双重变异限制策略的多策略粒子群优化算法(MSPSO)。模拟退火算法依概率动态更新惯性权重,平衡算法的探索与开发;饥饿游戏搜索算法根据粒子的“饥饿程度”(对寻找最优解的影响)优化粒子位置公式,加快粒子收敛;双重变异限制策略同时约束粒子位置和速度,避免粒子越界。通过与其他3种粒子群算法进行对比实验,在求解单模态问题时,MSPSO在适应度平均值、最小值、标准差3个方面能够获得更优数量级最优解,在求解多模态和固定维数问题时,MSPSO同样能获得更优值。此外,在求解云计算任务调度问题时,在总成本、适应度值最小化两方面MSPSO均表现出明显优势。当任务数为40时,MSPSO总成本比LWPSO、GWOPSO、EEAPSO低14.4%、15.3%、11.2%,这得益于动态的位置更新策略提高了粒子间信息交互能力,加快算法寻优效率,缩短任务执行时间。MSPSO适应度值分别低10.5%、10.6%、7.6%,这表明模拟退火算法在平衡算法探索与开发、避免陷入局部极值的有效性。在其他维度中,MSPSO在适应度值、总成本两个方面也表现出明显优势,验证了MSPSO在求解云计算任务调度问题中的有效性。 然而,随着任务数的增加,MSPSO在执行任务总成本方面的优越性有所降低。在未来工作中将考虑在负载均衡、资源利用率等方面进行改进,进一步优化算法性能,使其能够在大规模任务的场景中也表现出明显的优势。4.4 实验设置


4.5 性能指标

4.6 结果分析


5 结论
