基于阿基米德混沌精英鲸鱼算法的微电网优化

2023-11-04王骏玮岳云涛李炳华

科学技术与工程 2023年29期

王骏玮, 岳云涛*, 李炳华

(1.北京建筑大学电气与信息工程学院, 北京 100044; 2.悉地(北京)国际建筑设计顾问有限公司, 北京 100013)

随着清洁能源的不断发展,越来越环保经济的发电方式不断引入传统电力系统如光伏发电、风力发电等技术,为未来的能源问题提供新的解决思路。越来越多的企业工厂也拥有自己的微网系统以保障当供电系统出现问题时工厂仍可以全时段生产,并且合理利用清洁能源降低生产成本。文献[1]通过天鹰座优化算法改进算数优化算法提高算法性能,以埃及的微电网系统进行仿真。文献[2]通过分析印度境内多领域内的微网模型,通过仿真实验推断一种具有普遍使用价值的光伏设计模型,以实现环境和经济双重最优目标。文献[3]以可移动阻尼波算法作为框架,探究不同类型分布式电源所组成的微电网的设计问题。文献[4]提出了一种新型综合能源微网系统以经济和环保为目标,通过仿真结果验证其实用性和有效性。文献[5]选取植物传播算法,针对微电网中柴油发电机的大小和位置进行优化。文献[6]利用微分演化算法和其他算法,对埃及农村计划建造的微电网进行了可行性与经济性分析。文献[7]提出了一种动态控制的鲸鱼算法,优化各分布式电源的输出。文献[8]针对多能源的冷热电联供型微网的能量优化问题,使用长短期记忆网络预测负荷和可再生能源出力,提前进行规划,并采用改进鲸鱼算法优化其分布式电源输出,应用于楼宇系统中证明其有效性。文献[9]针对负荷需求和智能家居问题建立了三目标优化框架的微电网能源管理模型。文献[10]在经济性分析和可靠性约束上构建微网优化配置框架,以医院为对象进行优化配置,证明其方法具有适用性和有效性。文献[11]选用非支配排序的多目标差分进化算法对综合能源系统的多维可靠区间进行优化,研究供需响应对系统可靠性的影响,实际应用价值较高。

上述研究中,其研究重点大多在于微网建模方向,对于优化算法的理论研究较浅。鲸鱼优化算法具有结构简练、收敛速度快、精准度较高等特点,广泛应用于众多领域。但其存在容易陷入局部最优解,收敛速度过快导致无法广泛搜索解空间等问题。针对算法进行深入分析,现采用阿基米德螺线替换对数螺旋曲线,增加其局部搜索能力,通过tent映射提高初始种群随机性,加强其对解空间的覆盖,引入改进精英反向学习,提升算法跳出局部最优解的能力,并引入自适应参数调节其优化策略选择倾向,对算法进行全面改进。采用鲸鱼算法的7个基准函数对算法进行性能测试,然后建立微电网模型以经济性和环境治理费用最低为目标进行微网优化,经过仿真实验对比其他算法证明其有效性和实用性。

1 改进的鲸鱼优化算法

鲸鱼优化算法通过观察座头鲸多种捕食行为模式总结出数学模型,鲸鱼优化算法共有3种搜索解的方式,通过不同参数选择不同的策略进行寻优。

1.1 算法改进策略

1.1.1 阿基米德螺旋曲线

鲸鱼算法发泡网攻击模式选取的数学模型是对数螺旋曲线。通过图1所示可得对数螺旋曲线的螺距是不断变窄的,当面对具有众多局部最优解的问题时,这种搜索路径可能会错失有效信息的搜索导致较低的遍历性[12]。

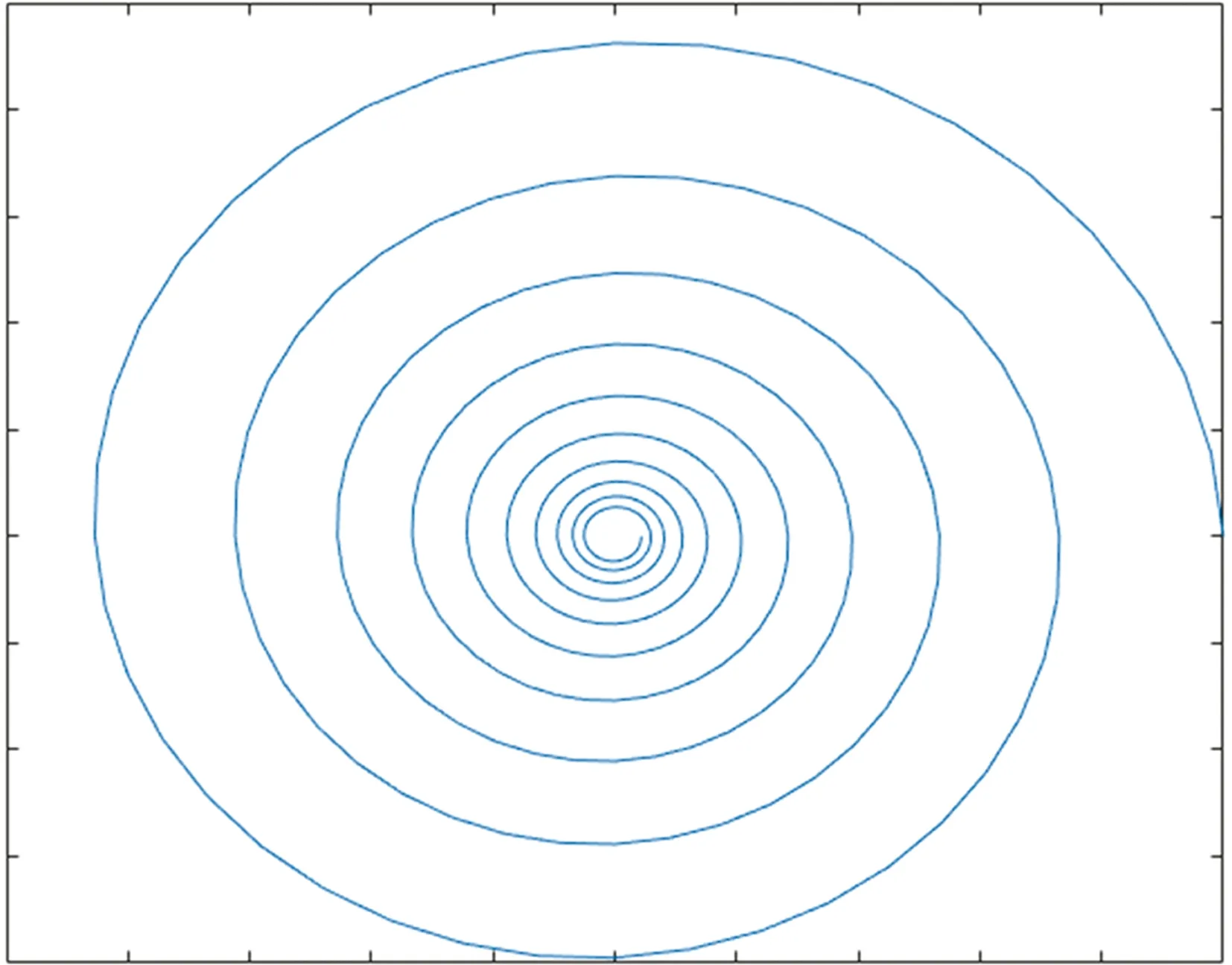
图1 鲸鱼算法对数螺旋搜索路径Fig.1 Whale algorithm logarithmic spiral search path

阿基米德螺线具有更均匀和更密集的搜索路径,如图2所示,可以充分地搜索附近的空间。其运动轨迹为一点以固定的角速度围绕这个点移动而产生的轨迹,其螺距为不变的常数,参数b参与对螺线螺距的控制[13]。

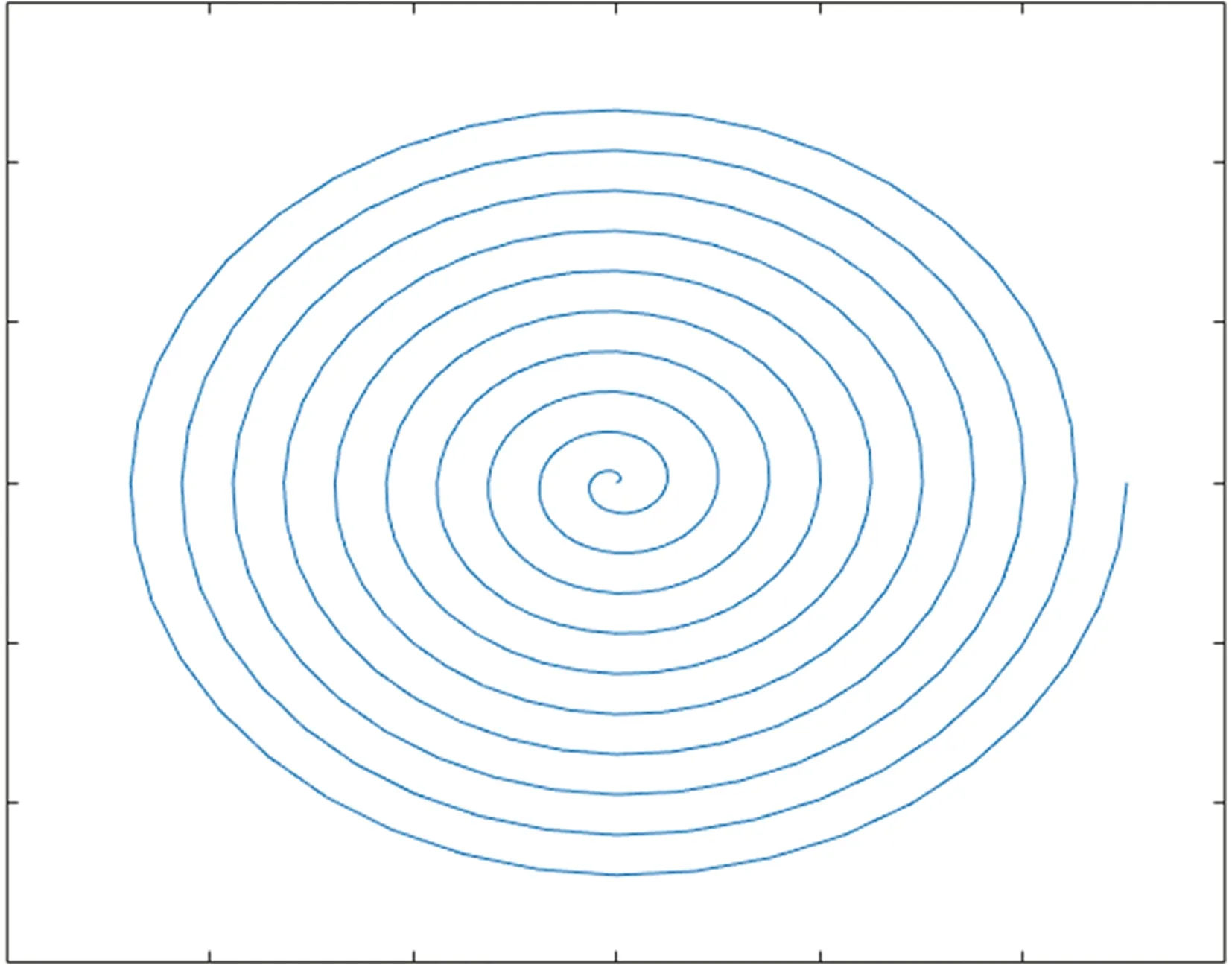
图2 二维等距阿基米德螺旋曲线图Fig.2 2D equidistant Archimedean spiral curve

(1)

X(t+1)=(D′bl)4lsin(2πl)+X*(t)

(2)

式中:a、b、l为螺旋母线参数;D为种群移动距离;X(t)为t最优解;X*(t)为t的代解。

1.1.2 改进精英反向学习

众多算法存在的另一个通病是容易陷入局部最优解。通过引入精英反向学习,当算法收到局部最优解的吸引时,增加了当前代的种群丰富性,传统的精英反向学习同样存在局限性,反向解的获得只与该种群的上下界有关系,当算法迭代至后期时,一味地选择远离背离局部最优解的反向可能会增加算法的优化负担。改进后的精英反向学习将传统反向学习中的上下界替换为当前算法迭代的种群中的最优与最差,保留了算法迭代过程中的经验,并且通过Ksd扰动因子增强反向学习的比重,更具有针对性。

Ksd=ln[1.2+(1.5T)/Tmax]

(3)

XT.BEST=Ksd(XT.BEST+XT.WORST)-XT.BEST

(4)

式中:Ksd为扰动参数;Tmax为最大迭代数字;T为当且迭代数;XT.BEST为T代最优解;XT.WORTS为T代最差解。

1.1.3 Tent映射

另一个影响算法性能的因素就是初始种群的质量。初始种群更随机,更均匀地分布在搜索空间中就可以更快找寻到全局最优解。tent映射是混沌映射的一种,相对于其他的混沌映射,tent映射的分布函数更为均匀,其产生的混沌序列更具有全局遍历性。

(5)

式(5)中:k为当前的种群数;Zk为第k个种群,其初始值为0.4;β为混沌参数,初始值选取为0.152,具有较好的随机性并且可以避免产生发散序列。

1.1.4 自适应参数

参数a作为控制算法下一步搜索策略的两个重要参数之一,通过调整a的取值倾向在算法中后期改变随机搜索的概率可以增强算法跳脱局部最优解的能力,由于鲸鱼算法较优秀的收敛速度和能力,适当减少螺旋收缩的方式不会对算法的收敛能力造成太大影响。改进后a的绝对值在大于1的部分相较于原始算法更多,加强搜索猎物倾向。

(6)

式(6)中:amax、amin分别为参数a的最大值和最小值。

2 微网成本模型和目标函数

2.1 微型燃气轮机发电成本模型

微型燃气轮机在高购电成本的情况下对降低运行成本有很大的影响[14-15]。微型燃气轮机的运行成本分为两部分。其中一个部分为污染成本,成本的另一部分是MT运营成本。污染气体排放指数和治理成本如表1所示[16-17]。

表1 MT和DT污染气体排放指数和治理费用Table 1 MT and DT pollution gas emission index and treatment cost

(7)

(8)

(9)

(10)

CMT=CMT_FUEL+CMT_OM+CMT_POL

(11)

式中:ηMT为MT的效率;PMT为微型燃气轮机功率;PMT_MAX为微型燃气轮机最大功率;CMT_ON为燃气轮机运行费用;KMT_ON为燃气轮机运行成本系数;CMT_FUEL为燃气轮机燃料费用;CMT_POL为燃气轮机污染治理费用;Dy、Hy为主要污染物治理成本系数;C为天然气价格,取值2.5 元/m3;LHV为低热值,选择9.7 kW·h/m3;KMT_ON为维护成本,0.012 kW/元;CMT为微型燃气轮机的总成本。

2.2 柴油发电机发电成本模型

仿真中柴油发电机的成本模型也分为运营成本和污染治理成本。

(12)

(13)

(14)

CDT=CDT_FUEL+CDT_OM+CDT_POL

(15)

式中:c1、c2、c3为柴油发电机的燃烧成本指数,c1=6,c2=0.12,c3=0.000 85;KDT_ON为柴油发电机的维护成本系数,其值为0.007 kW/元;CDT_ON为柴油发电机的维护成本;CDT_POL为柴油发电机的污染治理成本;CDT为柴油发电机的总成本。柴油发电机污染排放指数及治理费用如表1所示[16-17]。

2.3 能源存储装置

仿真试验中选择的储能装置为蓄电池组,操作成本为

(16)

式(16)中:KBT_ON为管理电池组费用的指标,选择0.005 kW/元;PBT(t)为t时刻蓄电池组输出功率;CBT_ON为蓄电池组运营成本。

2.4 光伏及风能发电成本

光伏及风电具有污染少、发电成本低等特点,仿真实验选取二者运营成本作为发电成本,其运营成本系数KPV、KWT分别为0.009 6 元/(kW·h)和0.45 元/(kW·h)。

(17)

(18)

式中:KPV、KWT分别为光伏、风机发电的运营成本系数;PPV(t)、PWT(t)分别为t时刻光伏、风机的输出值;CPV、CWT分别为光伏、风机发电成本。

2.5 目标函数及约束条件

为使运行成本和污染控制成本最小,将以上各模型的污染治理成本和运营成本求和即为目标函数。

PLOAD=PPV+PWT+PDT+PMT+PBT+PGRID

(19)

式(19)中:PGRID为微网与电网交互功率;PLOAD为负荷。

通过引入分时电价机制,及时选择合适的能源处理方式降低运营成本和购电成本。

(20)

F(t)=min(CPV+CWT+CMT+CDT+CBT+

CGRID)

(21)

式中:CGRID为向电力系统购买或出售电力的总价格;GGRID为分时电价。

根据每个设备的状态,每个设备的输出都有一个极限值,如表2所示,并为此设置约束条件。

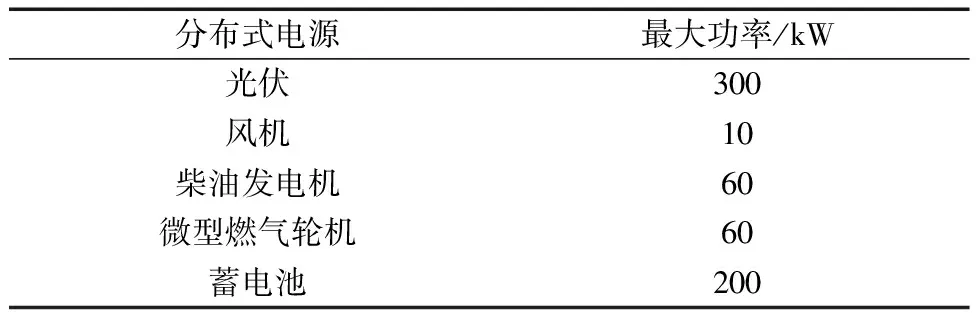
表2 分布式电源最大功率图Table 2 Maximum power diagram of distributed power supply

PN,min≤PN(t)≤PN,max

(22)

式(22)中:N为电源类型。

在保证储能单元及时消耗的前提下,还应保证储能元件的使用寿命,使电池不会完全充放电。每一次储能单元输出能源供给微网使用时,其剩余电量还需计算进下次的运算过程中,合理的积累和输出储能单元的能源也是提高能源利用率和降低运营成本的重要方法之一。

CSOC_min≤CSOC≤CSOC_max

(23)

CSOC(t+1)=CSOC(t)+BT_consume

(24)

式中:CSOC为当前时刻储能单元容量;CSOC_min为最大充电容量的0.3倍,CSOC_max为最大充电能力的0.95倍;BT_consume为储能单元消耗电量。

3 算法性能测试及微网优化仿真结果

3.1 算法性能测试

为了测试改进后的算法性能,采用文献[13]中鲸鱼算法的7个基准函数对算法性能进行对比,其中包括单峰基准函数和多峰基准函数,固定维多模基准函数,可以测试算法多方面性能,并探究测试其改进后的性能与原算法的差别,其表达式和最优值可以由表3可知。

表3 测试基准函数信息[13]Table 3 Test benchmark function information[13]

通过使用鲸鱼算法的基准函数不难发现,鲸鱼优化算法(whale optimization algorithm,WOA)在收敛精度和收敛速度上都优于原算法。在对图3、图4单峰函数的多次测试中,改进后的算法每次都可以快速地找到比初始算法更优解。在图5、图6测试中,算法初期出现了算法初期收敛速度和精度慢于原算法的情况,F3拥有非常多的局部最优解,算法在优化过程中极易陷入局部最优解中,改进后的鲸鱼算法后半程中因为精英反向学习的存在多次跳脱局部最优解从而寻找到更优解,证明其在多局部最优解问题中的能力。当面对图7～图9的固定位多模基准函数时,改进后的鲸鱼函数通过阿基米德螺线搜索路径在全优化周期中都表现出了更强的搜索强度,优于原始鲸鱼算法。

图3 F1目标函数及目标函数优化值Fig.3 Optimization value of objective function and objective function F1

图4 F2目标函数及目标函数优化值Fig.4 Optimization value of objective function and objective function F2

图5 F3目标函数及目标函数优化值Fig.5 Optimization value of objective function and objective function F3

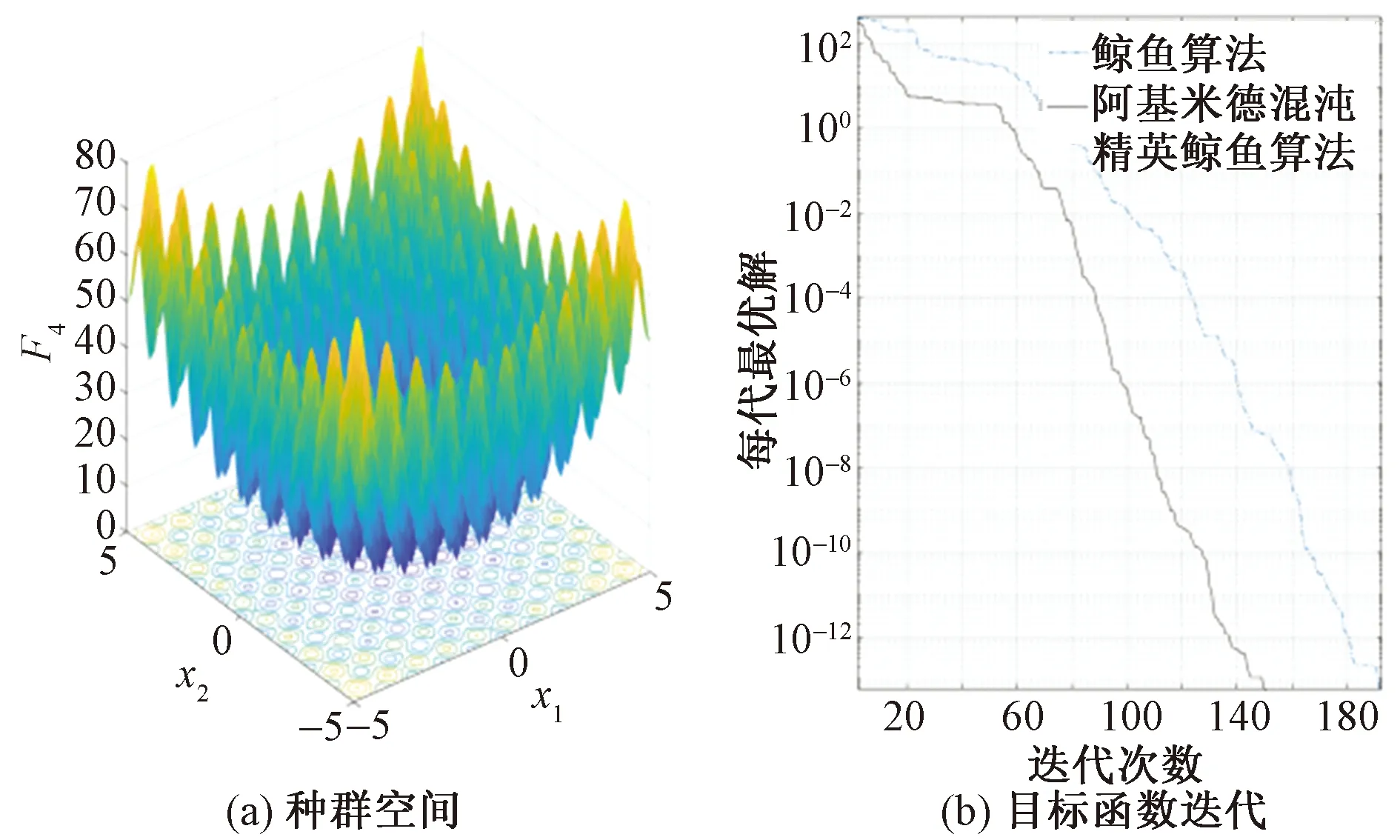
图6 F4目标函数及目标函数优化值Fig.6 Optimization value of objective function and objective function F4

3.2 微网仿真

该仿真实验基于某微电网的每日数据优化微电网各分布式电源的输出。清洁能源的产量和日负荷如图10所示。

图10 清洁能源输出与日负荷Fig.10 Clean energy output and daily load

选择了3种算法进行仿真实验,与改进的WOA进行比较,分别是鲸鱼优化算法(whale optimization algorithm,WOA)、粒子群优化算法(particle swarm optimization,PSO)和灰狼算法(grey wolf optimizer,GWO)。其中粒子群算法的最大速度为6,惯性常数最大值为0.9,最小值为0.2,加速常数c1、c2取值都为2。算法最大迭代次数为500次,初始种群规模规定为30个。

如图11、图12所示,仿真以1 h为优化节点,以第24小时优化结果为例进行分析。改进后的鲸鱼优化算法采用tent映射后首次迭代计算的目标函数值低于采用普通随机选取初始种群方法的其他算法的目标函数值,以最少的迭代次数进入较低的目标函数值。为快速地找到全局最优解提供有力支持,WOA通过随机选取的方法首次计算得出的目标函数值都相对较大。影响了收敛速度。在多次仿真试验中,发现WOA在本问题中表现不佳,极易陷入局部最优解中,PSO、GWO在多次迭代中也存在陷入局部最优解的问题。改进后的鲸鱼算法在初期通过阿基米德螺旋模型使算法具有更快的局部搜索能力,在初始种群质量较高的情况下能快速锁定收缩方向,在算法优化结束时改进的鲸鱼优化算法优化的目标函数值优于其他的算法。该算法具有较强的跳脱局部最优解的能力,在迭代初期就可以较快地搜索到全局最优解,收敛速度快,迭代次数优于其他算法,其结果也显著优于其他算法。

图11 第24小时优化结果初始种群优化值Fig.11 Initial population optimization value of optimization results in the 24th hour

图12 第24小时优化结果Fig.12 Optimization results in the 24th hour

通过改进算法优化后各电源输出如图13所示,在凌晨时间段,由于光伏和风能产能较少,系统主要通过购入较低的电网能源和相对廉价的柴油发电机完成负荷的供给,并且购入多余能源存入储能单元为后续高负荷时间段做准备。当9:00之后获得大量光伏能源后,系统在完成基本符合需求的情况下大量兜售多余的清洁能源实现盈利,并且降低柴油发电机和燃气轮机的输出,丰富的清洁能源也可以及时消纳并且存储少量部分以作备用。表4中4种算法日优化结果对比突出本文算法的优越性和有效性。