改进的多端柔性直流系统多点直流电压无差协调控制策略

2023-11-04李从善张晓伟和萍武小鹏赵琛

科学技术与工程 2023年29期

李从善, 张晓伟, 和萍, 武小鹏, 赵琛

(郑州轻工业大学电气信息工程学院, 郑州 450053)

随着能源结构的不断调整,大容量电力电子器件在电网中的渗透率逐步提高,在源、网、荷、储4个领域都呈现出电力电子化趋势。在输电系统方面,基于电压源换流器的多端柔性直流输电系统(voltage source converter based multi-terminal high voltage direct current, VSC-MTDC)是未来远距离输电技术的重要发展方向之一,逐渐成为新能源并网的最佳选择[1-3]。

目前,应用于VSC-MTDC系统的站间控制策略大致分为3种:主从控制、裕度控制和直流电压下垂控制[4-6]。其中下垂控制利用多个换流站的功率调节能力,实现不平衡功率的快速分配,直流电压响应特性较好,但是存在直流电压偏差较大的问题。

针对换流站采用下垂控制消纳不平衡功率时固有的直流电压偏差问题,国内外学者进行了大量研究,目前主要分为以下3种控制方法。

第一种方法是通过改进下垂系数,实现不平衡功率的合理分配,减小直流电压的偏差。文献[7-10]通过自适应调整下垂系数,有效减小了直流电压的偏差。然而,换流站实际有功功率传输值与参考值之间的偏差持续存在,直流电压偏差也一直存在,不利于系统的稳定运行。

第二种方法是通过改变换流站的运行方式来实现直流电压的无差调节。文献[11]提出将直流电压误差通过比例-积分(proportion-integration,PI)控制器叠加到有功功率环上,利用PI控制器的无静差特性,实现直流电压的无差调节。文献[12]提出一种结合主从控制和下垂控制的联合控制策略,通过切换控制方式,实现直流电压的无差调节。文献[13]提出一种多点电压协调控制策略,最小化换流站动态功率偏差的同时,提升了直流电压的性能。然而,上述控制策略的本质是将下垂站转变为定直流电压控制站,丧失了下垂控制多站协同消纳不平衡功率的优势。

第三种方法是通过调整有功功率参考值,达到直流电压无差调节的目的。文献[14]通过采集直流系统的不平衡功率,叠加到有功功率参考值上,实现下垂曲线的平移。文献[15]证明了在直流系统受到功率扰动后,各换流站保持输出功率不变的同时,无法将直流电压恢复至额定值。进而提出一种兼具换流站功率变化最小以及直流电压偏差最小的协调控制策略,实现直流电压的“伪”无差调节。

针对换流站采用传统下垂控制消纳不平衡功率时固有的直流电压偏差问题,现基于第三种方法,提出一种优化协调控制策略,将直流网络不平衡功率作为前馈补偿量注入传统下垂控制中,通过平移下垂曲线来实现直流电压的准无差调节。同时将偏差下垂控制引入定有功功率换流站,避免不平衡功率过大导致下垂站满载而失去控制直流电压的能力。最后,通过PSCAD/EMTDC建立五端VSC-MTDC仿真模型,仿真结果验证所提控制策略的有效性。

1 传统下垂控制电压偏差分析

1.1 VSC-MTDC系统模型

五端VSC-MTDC系统结构如图1所示。VSC1～VSC5代表5个电压源型换流站,直流侧通过直流网络并联,交流侧与各自的交流电网连接。

图1 VSC-MTDC系统结构图Fig.1 VSC-MTDC system structure diagram

单个VSC结构的拓扑结构如图2所示。

在三相坐标系下,Us为交流电网电压;Ua、Ub、Uc分别为交流电网电压;R、X分别为VSC交流侧等效电阻和电抗;C为直流侧电容;Udc为直流侧电压

在两相旋转dq坐标系下,VSC的数学模型为

(1)

式(1)中:L为交流侧等效电感;Usd、Usq分别为电网电压的d、q轴分量;Ud、Uq分别为 VSC交流侧电压的d、q轴分量;isd、isq分别电网电流的d、q轴分量;ω为电网电压矢量同步旋转角速度。

1.2 传统下垂控制电压偏差分析

类比传统发电机一次调频特性,下垂控制无需站间通信,利用直流电压与有功功率特性曲线,实现不平衡功率的快速分配和直流电压的稳定控制。直流电压-有功功率(Udc-Ps)控制器结构和特性曲线如图3和图4所示。

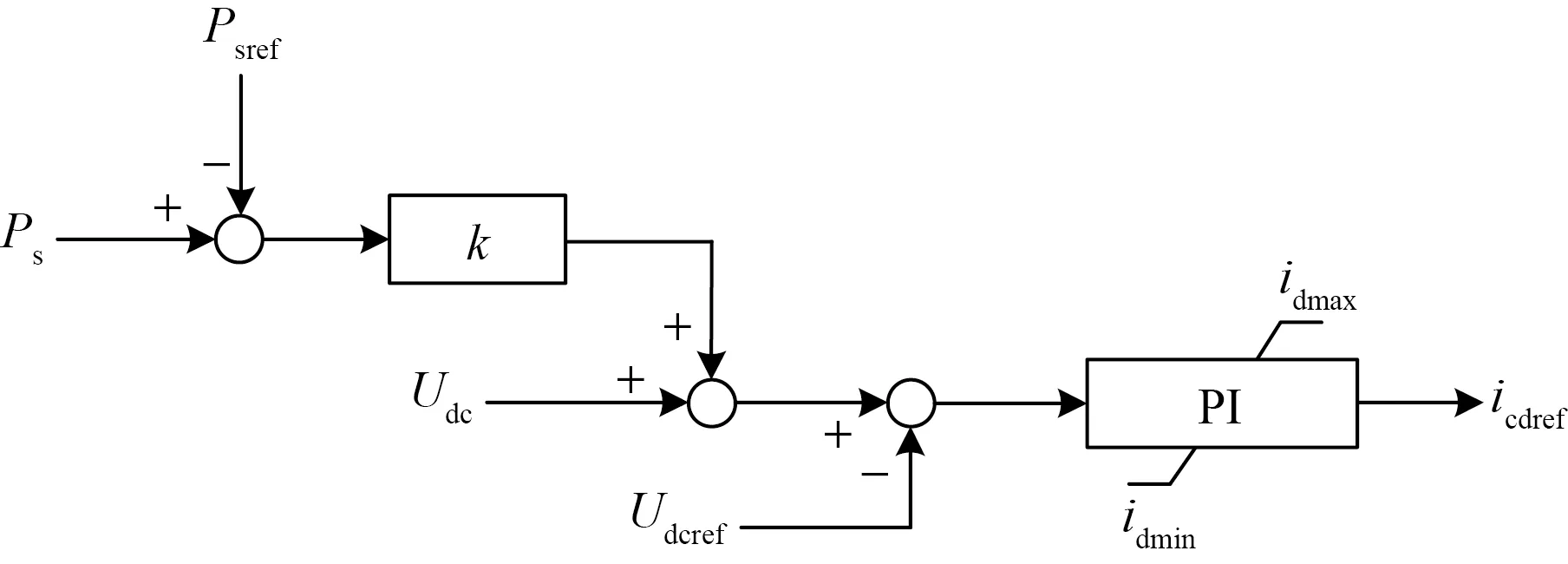
Udc和Udcref分别为直流侧电压实测值和参考值;Ps、Psref和Psmax分别为换流站有功功率实测值、参考值和额定容量;k为下垂系数

图4 直流电压下垂控制特性图Fig.4 DC voltage droop control characteristic diagram

在稳态情况下,由图3可得换流站直流电压与有功功率的关系为

Udc=Udcref+k(Ps-Psref)

(2)

假设直流系统有N个换流站,其中1～m个换流站采用传统下垂控制;m+1～n个换流站采用定有功功率控制,n+1～N个换流站采用定交流电压控制。

1～m个下垂站有功功率参考值之和Pr为

(3)

式(3)中:1≤i≤m。

m+1～n个定功率站有功功率之和Pt为

(4)

式(4)中:m+1≤b≤n。

n+1～N个定交流电压换流站有功功率之和Pw为

(5)

式(5)中:n+1≤j≤N。

根据图4,设初始稳态时,系统运行在状态1,当直流系统出现功率扰动ΔP时,m个下垂站利用自身下垂特性消纳不平衡功率的同时,系统稳定运行点也会随之移动。当再次达到稳态时,设系统运行在状态2,此时直流电压偏差为ΔUdc。由图4可知,下垂站i所承担的不平衡功率ΔPi与直流电压偏差ΔUdc存在以下关系

(6)

根据能量守恒,各个下垂站有功功率变化量之和应等于ΔP,即

(7)

联立式(6)与式(7),可得

(8)

(9)

由式(8)可以看出,ΔUdc与ΔP成正比,与m个下垂站的下垂系数倒数之和成反比。这说明,当直流系统功率发生波动后,所有下垂站会根据自身下垂曲线,协同消纳不平衡功率[18]。

由式(9)可以看出,下垂系数决定了下垂站在动态调节过程中所承担的不平衡功率的多少。若各换流站采用相同的下垂系数,则所有换流站均分不平衡功率;若各换流站采用不同的下垂系数,则下垂系数较小的换流站将承担较多的不平衡功率,下垂系数较大的换流站将承担较少的不平衡功率[19]。

2 改进的多点直流电压协调控制策略

2.1 改进下垂控制

针对换流站采用传统下垂控制消纳不平衡功率固有的直流电压偏差问题,提出一种改进的VSC-MTDC系统多点直流电压优化协调控制策略,将不平衡功率作为前馈补偿量注入下垂控制中,通过平移下垂曲线来实现直流电压的准无差调节。优化协调控制策略的特性曲线如图5所示。

图5 优化协调控制原理图Fig.5 Optimization of coordinated control schematic diagram

设初始稳态时,系统运行在状态1,当直流系统出现功率扰动ΔP时,给各个下垂站一个前馈补偿量,大小为ΔPi。此时系统稳定运行点从Ai变为Di,实现下垂曲线的平移。Pisref和P″i分别为换流站调整前后的有功功率参考值,满足

P″i=Pisref-ΔPi

(10)

而后换流站根据下垂特性消纳不平衡功率,最终系统稳定运行在Ci点附近,实现直流电压的准无差调节。与传统下垂控制相比,换流站传输的有功功率并没有发生改变,而直流电压偏差近似为零,系统的稳定性得到大幅提高。

2.2 功率平衡分配方案

为了将直流系统中的不平衡功率合理分配给各个下垂站,将换流站的可用功率裕度引入功率分配系数上,快速调整有功功率参考值[20]。

P″i=Pisref-(Pimax-Pisref)×

(11)

式(11)中:Δt为系统采样时间。在该功率平衡分配方案下,控制系统只需采集非下垂站的有功功率值,当且仅当直流系统潮流发生变化时,才向下垂站更新有功功率参考值。其余情况下,下垂站只需根据最近一次更新的有功功率参考值稳定运行。同时该功率平衡分配方案对站间通信要求极低,即使当各换流站通信中断时,仍能按传统下垂控制方式正常运行。

2.3 直流电压偏差下垂控制

(12)

式(12)中:kb为直流电压偏差下垂系数;Pbmax为定功率站的最大容量。

定功率站采用偏差下垂控制,在直流电压超过设定的运行范围时,设直流系统中余下的不平衡功率为ΔP*。当系统再次达到平衡时,采用偏差控制换流站的有功功率为

(13)

式(13)中:P′b为系统稳定后采用偏差控制换流站的有功功率。

对于图1所示的五端系统,VSC1和VSC2采用优化下垂控制,VSC3和VSC4采用直流电压偏差下垂控制,VSC5采用定交流电压控制。系统控制特性曲线如图6所示。

图6 系统控制特性曲线Fig.6 The overall control characteristic curve of the system

3 仿真与分析

基于PSCAD/EMTDC仿真软件搭建了如图1所示的五端VSC-MTDC系统,具体仿真参数见表1。通过3个仿真算例,利用3种控制方法对比,验证所提控制策略的有效性。

表1 系统仿真参数Table 1 System simulation parameters

控制方法1(CM1):传统下垂控制。

控制方法2(CM2):优化协调控制。

控制方法3(CM3):优化协调控制+偏差下垂控制。

3.1 直流网络出现功率盈余

t=3 s时,VSC3有功功率指令值由115 MW增至185 MW,仿真结果如图7所示。

图7 系统功率增加仿真Fig.7 System power increase simulation

由图7可以看出,由于系统存在损耗,所以换流站有功功率、系统直流电压实际值与参考值之间略有差别。设ΔP1～ΔP5为VSC1～VSC5有功功率变化量。t=3 s时,直流系统出现功率盈余,在CM1作用下,VSC1和VSC2按照传统下垂控制消纳不平衡功率,当系统达到稳态时,ΔP1和ΔP2分别为23.5 MW和46.5 MW,ΔUdc为7.09 kV,直流电压偏差率为1.77%。在CM2作用下,ΔP1和ΔP2分别为16 MW和54 MW,ΔUdc为0.14 kV,直流电压偏差率为0.035%,实现了直流电压的准无差调节;同时系统将较多的不平衡功率分配给功率裕度较大的换流站,所以VSC2承担的不平衡功率多于VSC1,避免VSC1满载。由于直流电压未超过系统设定的运行范围,所以CM3作用下的仿真结果与CM2相同。

3.2 直流网络出现功率缺损

t=3 s时,VSC3有功功率指令值由115 MW降至45 MW,仿真结果如图8所示。

图8 系统功率减小仿真Fig.8 System power decrease simulation

t=3 s时,直流系统出现功率缺损,由图8可以看出,在CM1作用下,ΔP1和ΔP2分别为23.5 MW和46.5 MW,ΔUdc为7.03 kV,直流电压偏差率为1.76%。在CM2作用下,ΔP1和ΔP2分别为42 MW和28 MW,ΔUdc为0.11 kV,直流电压偏差率为0.028%。此时VSC1的功率裕度多于VSC2,所以VSC1承担的不平衡功率多于VSC2。

3.3 换流站退出

t=3 s时,VSC2退出运行,仿真结果如图9所示。可以看出,在CM1作用下,VSC1作为唯一的功率平衡点,很快达到满载并切换成定有功功率运行,失去了控制直流电压的能力,直流电压将继续下降。在CM2作用下,由于VSC3和VSC4控制方式仍然为定有功功率,并不参与系统功率的调节,所以ΔP3和ΔP4都为0 MW。在CM3作用下,在直流电压下降至390 kV时,VSC3和VSC4由定有功功率控制转变为下垂控制,协同VSC1消纳不平衡功率,承担起稳定直流电压的任务。在系统进入稳态后,ΔP1、ΔP3和ΔP4分别为26、41和33 MW,ΔUdc为14.49 kV,直流电压偏差率为3.62%。同时VSC1并没有达到满载,还具备稳定直流电压的能力,系统的稳定性得到了较大的提高。