基于FOA-BP 神经网络的悬点示功图反演技术
2023-11-03卢玉
卢玉
辽河油田分公司钻采工艺研究院
抽油机井示功图代表着悬点载荷与位移在一个冲次内的关系,能够实时反映井下抽油杆、抽油泵的运行情况以及油井的工况状态[1]。目前,抽油机井示功图大多采用示功仪获得,存在投资成本高、维护成本高、数据易漂移失真等问题,制约了油井智能化管理的发展。电参数是抽油机井运行最基本的参数,具有普及率高、采集成本低、数据稳定等优点,应用电参数进行抽油机井示功图转化,可以取代示功仪,实现油井数字化、智能化管理[2]。
目前基于电参数反演示功图的方法分为扭矩系数法和智能学习法。S.G.GIBBS[3]提出了一种通过测量电动机转速从而间接获取抽油机井悬点示功图的方法计算出悬点载荷。杨敏嘉[4]根据电动机的电磁转矩计算方法,采用扭矩系数法建立了电参数和悬点载荷的对应关系,进而求出悬点载荷。张世荣[5]采用滤波和平滑处理技术对电动机功率曲线进行处理,并对上下死点附近的悬点示功图曲线再次进行平滑处理,从而得到修正数据。王卫江[6]等人提出了一种基于神经网络的抽油机悬点载荷反演算法,实现电动机输入电功率到悬点载荷之间的非线性拟合,间接获得悬点示功图。孙金根[7]提出了将悬点位移、电动机功率、电动机电枢电流和电动机转速作为神经网络的输入,间接预测出了悬点示功图。ZHANG[8]等人提出一种基于深度学习技术的电参数间接预测悬点示功图的新方法,将实测电动机功率曲线作为智能学习模型的输入参数,改善了电动机功率与光杆负载之间的一一对应关系。WEI[9]等人提出一种基于混合建模的电参数间接获取悬点示功图的方法,通过机构模型初步计算出悬点载荷并求出与实测载荷之间的误差,通过误差获得近似真实载荷的悬点载荷。武勇[10]将GA 遗传算法中遗传操作引入到PSO 粒子群算法中,建立了基于GAPSO-ELM 的示功图反演模型。利用扭矩系数法时在上下死点位置量级较小甚至为零,将其作为除数时误差较大,而基于智能学习方法时则难以考虑抽油机结构参数及平衡对学习模型的影响。
针对以上问题,提出一种基于果蝇(FOA)算法优化的BP 神经网络模型的电参数反演示功图的方法,将光杆功率与抽油机的扭矩因素相结合,消除了抽油机机型及平衡状态对示功图反演的影响,实现更高效、准确的悬点示功图反演。
1 悬点载荷与电动机功率关系
抽油机工作时,悬点载荷及平衡重力在曲柄轴上造成的扭矩与电动机传递至曲柄的扭矩相平衡。因此,基于抽油机结构参数可以建立悬点载荷及平衡与曲柄轴扭矩及电动机功率的关系模型。
由图1 可看出,以曲柄为研究对象,克服抽油杆柱和油柱载荷,减速箱曲柄轴净扭矩、曲柄平衡块重力与曲柄自重的等效载荷所产生的扭矩以及连杆拉力的切向力所产生的扭矩,由曲柄平衡条件得到[11-13]:
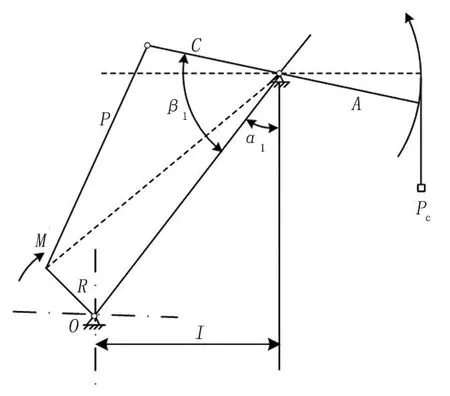
图1 游梁式抽油机运动简图Fig.1 Motion diagram of beam pumping unit
式中:M为减速箱曲柄轴净扭矩,kN·M;Qe为曲柄平衡块重力与曲柄自重的等效载荷,kN;T为曲柄平衡块重力,kN;R为曲柄平衡块重心到曲柄旋转中心的距离,m;θ为—曲柄转角,rad。
式中:Pc为悬点载荷,kN;A为游梁前臂长度,m;C为游梁后臂长度,m;α1为游梁前臂与旋转中心夹角,rad;β1为游梁后臂与连杆之间的夹角,rad。
由公式(1)~(3)组合可得
考虑四连杆传动效率η3,任意曲柄转角θ,曲柄轴净功率为
式中:Nq为曲柄轴净功率,kW;K1为系数,上冲程时取1,下冲程时取-1;η3为抽油机四连杆机构的传动效率;ω为曲柄角速度,rad/s[14]。
则电动机瞬时输出功率Ndc为
式中:Ndc为电动机瞬时输出功率,kW;K2为系数,M≥0 时取1,M <0 时取-1。
组合公式(4)~(6)即可得到悬点载荷与电动机输出功率的关系模型,可以看出由电动机功率反演悬点示功图时,如忽略扭矩因素及平衡参数的作用,模型难以适用于不同机型及不同平衡参数。
2 输入数据处理
为考虑抽油机机型、平衡参数对悬点示功图的影响,提高示功图的反演精度,通过一次训练实现不同机型及平衡参数下电动机功率到悬点示功图的反演,首先通过抽油机的平衡参数,即平衡重扭矩特征,将电动机功率转化为光杆功率,转化关系为
式中:Pg为光杆功率,kW;N为抽油机冲速,min-1;η1、η2、η3分别代表电动机效率、传动皮带效率、减速器效率,%。
通过公式(7)的转换,避免了抽油机平衡重对功图的影响。为了使建立的反演功图模型具有普适性,还需进一步考虑不同游梁式抽油机的结构参数。通过上述理论分析,抽油机的结构参数特征主要体现在抽油机的扭矩因数上。在电参反演示功图的输入参数中,结合抽油机的结构参数、平衡参数等,在示功图反演的过程中,将光杆功率与扭矩因数通过神经网络进行训练,将其作为网络模型的输入,通过模型训练得到输出载荷Pc与冲程的关系,完成示功图的反演。
3 神经网络模型的建立
BP 神经网络通过梯度下降法调整权重的大小,该方法沿着局部最优的方式进行调整,初始权值阈值的设置一般是根据经验或随机确定,增加了算法的求解时间,收敛速度慢,并且很容易出现局部寻优能力强,而全局寻优能力差的情况。因此,提出基于FOA 优化BP 神经网络算法,改进网络的求解速度和精确性。
FOA 优化BP 神经网络的原理如下:根据FOA迭代寻优中个体位置的变化对应BP 神经网络中的权值与阈值的更新值,个体位置的最佳值即对应于权值与阈值的初始最佳值,可以消除因为经验试凑所带来的影响,从而达到优化BP 神经网络的学习能力和运行速度[15-16]。
本文FOA-BP 神经网络模型主要构建过程:
(1)将需要优化的初始权值和初始阈值作为果蝇个体位置坐标,迭代次数,种群中个体数量进行初始化。
(2)将神经网络模型中载荷实测值和计算值的均方误差作为味道浓度判定函数F,根据FOA 优化算法步骤迭代更新最优位置坐标,其中F为:
式中:Pi′为载荷的实测值;Pi为载荷的计算值。
(3)不断更新调整权值,减小输出与期望间的误差,直到达到最大迭代次数或满足收敛条件。
通过收集抽油机井的历史电功率和实测悬点示功图数据,把所采集的电功率曲线转化为光杆功率曲线,将光杆功率曲线和悬点载荷作为训练样本集,采用果蝇(FOA)算法优化BP 神经网络的权值参数和阈值参数,并在此基础上建立基于FOABP 神经网络的示功图反演模型。通过小波变换[17]对神经网络模型的载荷预测值进行后处理,对悬点载荷进行预测,实现示功图的反演。示功图反演流程如图2 所示。

图2 神经网络示功图反演流程Fig.2 Neural network indicator diagram inversion process
4 建模和验证
根据神经网络及抽油机扭矩因数相关理论,建立FOA-BP 神经网络,神经网络的输入为光杆功率Pg与扭矩因数TF;网络的输出为悬点载荷Pc;隐含层节点个数设定为25。
经过多次训练试验的对比,BP 神经网络的训练参数设定为:输入层到隐含层的传递函数使用tan-sigmoid 函数;隐含层到输出层的传递函数使用linear 函数;最大训练次数1 000;学习速率0.3;动量因子0.15;目标误差0.01。FOA 果蝇算法中,设定种群规模为50,最大迭代次数为200。
采集不同机型抽油机的800 组电参数据,其中640 组作为训练样本建立训练的网络模型,其余160 组作为测试样本测试反演结果的精度,通过640 组训练样本,利用设定好的训练参数,获得训练好的基于FOA-BP 网络的反演模型,模型的寻优迭代路径如图3 所示。

图3 FOA-BP 网络迭代寻优路径Fig.3 FOA-BP network iterative optimization path
由图3 可知,模型在68 次迭代后达到最优,曲线趋于平稳,此时FOA-BP 网络反演模型趋于收敛,均方误差稳定在0.00752,能够用来反演示功图。为了分析反演模型预测结果的精度以及不同机型反演的普适性,可通过下面3 个指标对悬点示功图计算精度进行分析。
(1)最大悬点载荷的相对误差
式中:PMmax为实测示功图最大载荷值,kN;PCmax为计算示功图最大载荷值,kN。
(2)最小悬点载荷的相对误差
式中:PMmin为实测功图最小载荷值,kN;PCmin为计算功图最小载荷值,kN。
(3)悬点载荷均值的相对误差
式中:PMA为实测示功图悬点载荷平均值,kN;PCA为计算示功图悬点载荷平均值,kN。
通过对160 组测试数据的计算,悬点最大载荷的精度为95.23%,悬点最小载荷精度为94.59%,悬点载荷平均值精度为95.71%,基于FOA-BP 网络建立的模型反演的平均精度为95.18%,高于当前扭矩系数法不大于90%、智能学习算法低于95%的精度[16-18],验证了模型的准确性与适用性。
5 实例计算
利用所建立的FOA-BP 网络反演模型,选取现场5 口油井,在获得原始油井功率数据、平衡重参数的条件下,分别以各油井的扭矩因数和光杆功率作为模型的输入条件,得到1-26-4 井(机型CYJY8-3-37HB)、2-231-231 井(机型CYJY10-3-53HB)、1-40-1 井(机型CYJ10-3-37HB)、2-16-26 井(机型CYJ6-2.5-26HB)和1-16-x4 井(机型CYJY8-3-37HB)反演示功图,并与实测示功图进行对比分析,如图4~图8 所示:

图4 1-26-4 井实测与计算数据示功图对比Fig.4 Comparison of measured and calculated data indicator diagrams of Well 1-26-4
(1)1-26-4井(N=3.76 min-1)计算结果如图4所示,最大载荷误差4.92%,最小载荷误差5.09%,平均误差5.01%。
(2)2-231-231 井(N=4.3 min-1)计算结果如图5 所示,最大载荷误差7.93%,最小载荷误差8.24%,平均误差8.09%。

图5 2-231-231 井实测与计算数据示功图对比Fig.5 Comparison of measured and calculated data indicator diagrams of Well 2-231-231
(3)1-40-1井(N=4.28 min-1)计算结果如图6所示,最大载荷误差2.59%,最小载荷误差2.77%,平均误差2.68%。
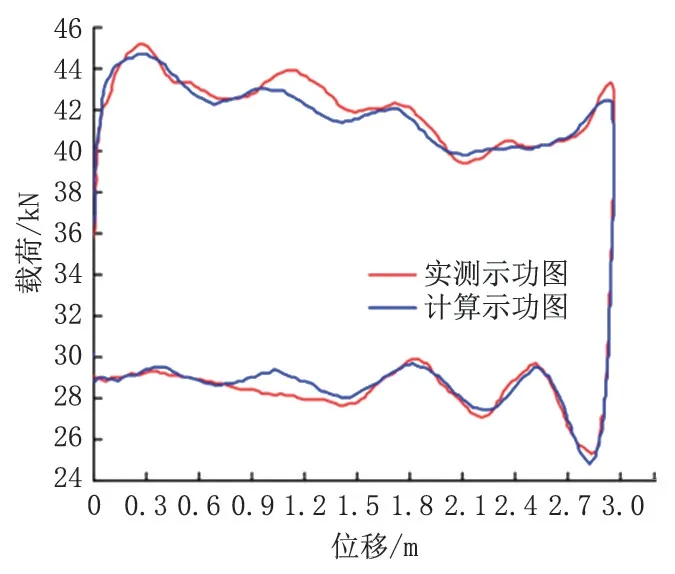
图6 1-40-1 井实测与计算数据示功图对比Fig.6 Comparison of measured and calculated data indicator diagrams of Well 1-40-1
(4)2-16-26 井(N=2.13 min-1)计算结果如图7 所示,最大载荷误差3.66%,最小载荷误差4.89%,平均误差4.28%。

图7 2-16-26 井实测与计算数据示功图对比Fig.7 Comparison of measured and calculated data indicator diagrams of Well 2-16-26
(5)1-16-x4井(N=3.8 min-1)计算结果如图8所示,最大载荷误差4.78%,最小载荷误差7.66%,平均误差5.25%。
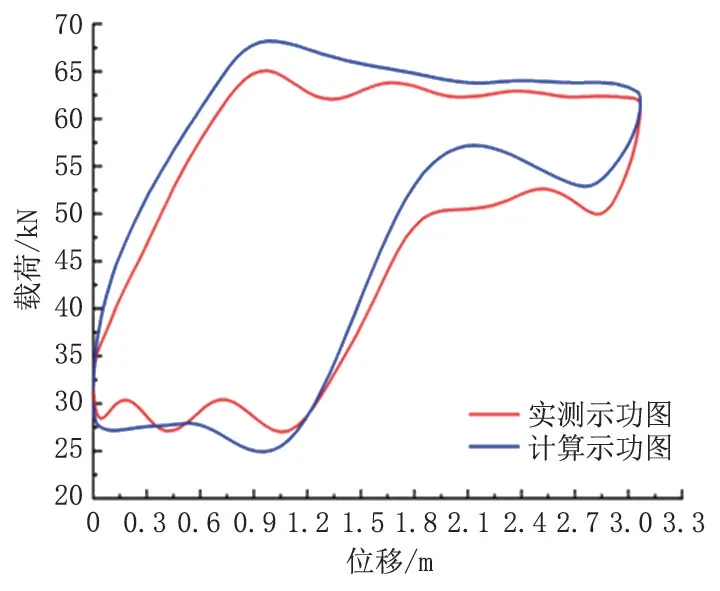
图8 1-16-X4 井实测与计算数据示功图对比Fig.8 Comparison of measured and calculated data indicator diagrams of Well 1-16-X4
6 结论
针对现阶段游梁式抽油机悬点示功图测量难度大、精度低等问题,提出了一种基于果蝇(FOA)算法优化BP 神经网络模型的电参数反演示功图的方法,实现了由实测电动机功率到悬点示功图的反演:
(1)由游梁式抽油机结构及平衡参数,建立了抽油机悬点载荷与电动机功率计算模型。
(2)基于电参数与输出悬点载荷之间存在的非线性关系,提出了一种基于FOA-BP 神经网络的悬点示功图计算方法,将光杆功率与扭矩因数作为输入参数,消除了抽油机结构、平衡参数的影响。
(3)利用800 组不同机型实测电动机功率开展了模型训练与测试,悬点载荷计算平均相对误差为95.18%,验证了模型的可行性。
