改进FCOS算法正样本选择的交通标志检测

崔港涛，马社祥

(天津理工大学 电气电子工程学院，天津 300382)

0 引 言

交通标志检测和识别(TSD&R)是必不可少的交通标志检测或现代自动车辆驾驶技术。作为车辆行驶的指引标志，交通标志被设计成不同的形状、颜色和独特的象形图，方便辨认和最大化。尽管这样设计，但是提出算法检测时用到的交通标志形状信息很少。近些年，由于深度学习检测速度快的同时能够保证精度，大量的算法出现并用在交通检测系统中[1]。

早期基于深度学习的目标检测器是两阶段的，建议框生成后回归框分类的方法如Faster-RCNN[2]，在第一阶段，生成一组感兴趣区域，并在第二阶段由卷积神经网络对它们进行回归分类。后来，单阶段的端到端检测算法得到了越来越多的关注[3，4]，其中建议框被预定义的anchor所取代，结构更简单速度更快，但是anchor必须密集地覆盖图像，其位置和尺度都需要手动调整，以最大化召回率；单阶段算法在训练中还存在产生的正负样本不平衡性问题。针对anchor的缺点，已经提出了几种方法来改变anchor的分配和提高其质量[5，6]，以避免一些极端的前景背景不平衡。近些年也提出了一阶段anchor-free方法，来避免anchor设置复杂的问题，有两组突出方法，第一组是基于关键点的自下而上的方法，在CornerNet[7]的开创性工作之后得到推广，这组算法通过检测目标的关键点(如角点、中心点和极值点)，然后对它们进行回归预测从而达到目标的检测；第二组anchor-free物体检测器遵循自上而下的方法[8]，直接对提取后的特征图中每个位置进行类和边界框坐标的预测。

FCOS算法作为一种自上而下的anchor-free物体检测器，在输入图像通过特征提取网络提取特征和FPN[9]特征融合之后，在其检测图像上落在真值框内的特征被标记为正，其它特征被标记为负，但在这些正面标记的特征中并不是每一个都有助于损失函数进行计算训练。因为这些正标签中的一些可能是完全错误的或者质量很差，由于交通标志目标小形状类似并且只有标志的中心位置具有分辨信息，所以这个问题在交通标志的检测中被放大[10]，这会在训练过程中注入了大量的标签噪声，影响最后模型的检测精度值。FCOS算法中的回归位置的选取方法使得正样本标签的质量差，导致检测器性能不高，本文基于FCOS算法设计一种融合交通标志形状特点的正样本标签选择策略，去除大量的正样本标签噪声，最终的在TT100K(tsinghua-tencent 100K)数据集的检测效果比改进前FCOS算法效果好。

1 FCOS算法

FCOS算法是anchor-free的单阶段目标检测算法，是在基于anchor的目标检测方法上分析提出的。此前提出的基于anchor的检测器，取得了不错效果，但是注意到基于anchor的检测器存在一些不足，检测性能对anchor的大小、纵横比和数量很敏感。例如，在RetiaNet[11]中，改变上述的超参数在coco数据集中的map降低4%[11]，鉴于此，FCOS算法去除anchor的设置，去除了大量不确定的超参数，因此比一些基于anchor的检测器检测效果要好，图1是FCOS算法整体结构。

图1 FCOS整体结构

FCOS算法通过特征提取网络进行特征提取，对相对原图缩放尺寸为1/8、1/16和1/32特征图进行类似FPN自下往上的特征融合，融合后分成5部分，缩放尺寸分别为1/8、1/16、1/32、1/64和1/128。对预测这5个不同级特征图上的位置特征进行目标类别和目标框的预测，每级缩放尺度不同，预测不同大小的目标，通过这样多级预测来提高召回率和解决由重叠包围盒引起的歧义。与基于anchor的检测器不同，基于anchor的检测器将输入图像上的位置视为多个anchor框的中心，并以这些anchor框进行回归目标边界框，FCOS算法直接在该位置进行正负样本选择训练回归目标边界框。预测模块对目标的分类预测时，预测数目大小为H×W×C，H和W分别为特征图的长和宽，C为预测的种类。对目标回归部分预测数目大小为H×W×4， 每个回归位置点的4个值l*，t*，r*，b*分别表示目标框内回归位置点离框的左边、上边、右边、下边的距离。设位置坐标为 (x，y)， 则该位置训练的回归目标可以表示为

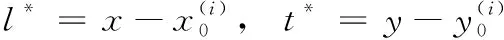
(1)

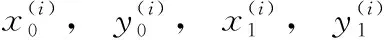
除了对分类和目标框预测，对特征图上每个位置预测Center-ness值，这个简单的方法能够用来抑制低质量的检测到的边界框，并且不用引入其它超参数，公式为

(2)

式中：centerness*的范围是0～1，通过将预测的centerness*值乘以相应的分类分数来计算最终分数。

训练损失函数为

(3)

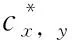
类别损失是对每个类别作二分类，用focal loss[12]方法计算

(4)

式中：γ因子使得减少易分类样本的损失，使得模型更关注于困难的、错分的样本，因子∂用来平衡正负样本本身的数量比例不均。

回归损失用GIoU计算[13]。公式为

(5)

式中：D和F分别为两个预测对象框，V为包住它们的最小方框。V(D∪F) 的面积为V的面积减去D∪F的面积。

2 算法设计

数据集真实框中目标特征分布在框中的位置是随机的，FCOS中直接将其真实框的中心作为目标特征的中心，这样显然会影响检测效果，目前还没有很好的方法确定目标的中心特征点。但是由于交通标志形状特点是固定的，在算法中，可以结合其特点设计新的正样本选择方法，更加合理设置目标中心点，同时提出与交通标志类别形状相对应的收缩方法进行交通标志正样本选择。

2.1 交通标志形状特点

交通标志种类多，每类交通标志有固定的形状信息。按照交通标志的功能，我国把交通标志分为三大类：警告、禁止和指示。

警告标志：具备对驾驶员的警告作用，标志颜色是以黄色为背景，外框被黑色包围，内部标志内容也是黑色。在形状特点上，将其设计成正三角形，如图2(c)部分。禁令标志：具备禁止作用，用于规范驾驶员的交通行为。标志颜色是以白色为背景，外框被红色包围，内部所标识的内容由黑色和红色线条组成，标志形状特征主要有圆形，如图2(a)部分；指示标志：具备指示行驶人员行进作用，用于改善交通情况。标志颜色是以蓝色为背景，内部标志内容是白色。在形状特点上，主要将其设计成圆形、矩形，如图2(b)部分。

图2 交通标志示例

上述对我国交通标志的形状信息分析，可以得到不同的交通标志有不同的形状。目标检测网络训练时这些信息是已知的，依据真实框目标的类别可以判断出其形状是三角形、圆形和矩形等的哪一种，利用获得的这些形状的特点信息，可以对目标的特征中心点重新设置，并且数据集信息的不同，正样本设置时的尺度放缩也不是矩形的时候最好，在交通标志数据集中，根据不同类别的形状特点进行放缩更加合理。

2.2 结合特点的正样本选择策略

上节中分析了交通标志形状特点，根据交通标志的类别能够判断出对应交通标志的形状。在原算法中，对于图3中的真实目标，无论是三角、矩形和圆形都按照矩形处理。本节设计将正样本标签选择与交通标志的形状特点相结合的更合理正样本标签选择策略。由于交通标志圆形和三角形居多，下面对这两类交通标志正样本选择策略设计说明。

图3 圆形交通标志真实框

圆形特点的交通标志，在原算法中，直接按照矩形框进行处理，但是为了获得更高质量的特征点，需要取目标特征中心点附近的位置点为正样本标签。基于圆形交通标志的目标特征中心点与真实框中心点正好吻合，中心位置选择不用进行处理，但是原算法样本选择时对应的是矩形收缩，根据圆形交通标志的结构特点，将矩形放缩变成圆形放缩更加合理。首先设置一个缩放因子[14]，但是放缩后不是直接按照放缩后的矩形区域作为正样本区域，而是根据圆形的交通标志的形状特点做一个内切圆，其内区域代替原来的矩形框区域为正样本选择区域，如图4所示。

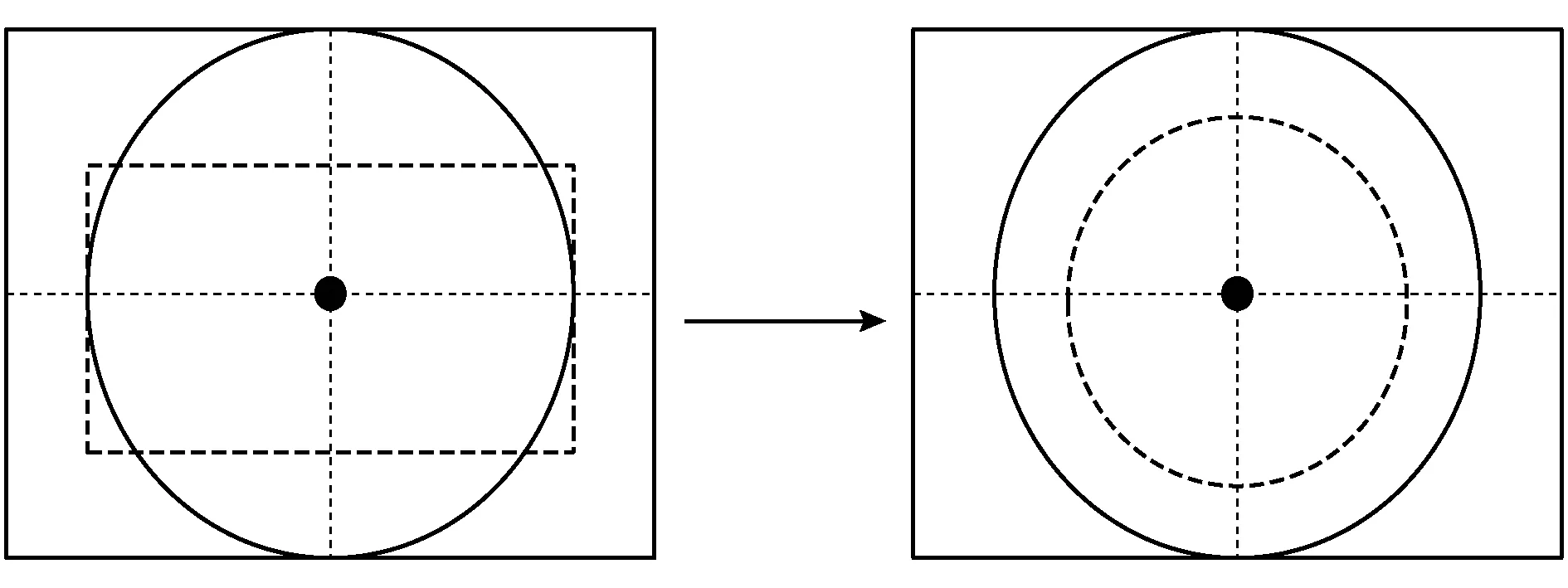
图4 结合圆形交通标志正样本选择

图4中前后真实框和圆形交通标志的中心点吻合，但是由于圆形交通标志的特征信息是包含在圆内的，所以将矩形正样本区域更换成圆形区域更加合理。本文设计对应正样本选择策略，当真实目标框不收缩时，将内切圆作为正样本区域能够去除对应的噪声信息，对应图中的实线内切圆。此时的目标特征中心点是圆心即图中的实心黑点，当以其为中心按照圆形收缩时，对应右图的虚线圆，以获得更高质量的正样本。

三角形特点的交通标志如图5所示，原算法中也直接按照矩形框进行处理，但是三角形交通标志面积只占真实目标矩形框的1/3左右，设置矩形框作为正样本区域会引入大量的噪声信息，而且从图6中可以观察到，相比圆形交通标志，接近矩形框的中心位置存在更多噪声信息。除此之外，在图中实心圆点为真实目标矩形框中心点，空心圆点为三角形交通标志特征中心点，两点不是同一个点，而算法中将矩形目标真实框中心作为正样本区域中心点显然不合理。当真实目标框不收缩时，将内接三角形作为正样本区域能够去除对应的噪声信息，对应图中的黑色三角形。此时的目标特征中心点是三角形中心点，对应右图中的空心圆点，当以其为中心按照三角形收缩时，对应右图的虚线三角形，以获得更高质量的正样本。下面对三角形特征中心点进行计算。

图5 三角形交通标志真实框

设目标真实框的按顺时针顺序4个顶点坐标分别为 (m1，n1)，(m2，n2)，(m3，n3)，(m4，n4)， 则3个顶点坐标分别为：((m1+n2)/2，(m1+n2)/2))，(m3，n3)，(m4，n4)。 对应的中心点坐标 (m，n) 为

(6)

位置点是否在圆和矩形框中很好判断，现在具体讨论判断一个点是否在三角形正样本区域内中。设点M在三角形ABC内，可以利用点M与点C在边AB同侧、点M与点B在边AC同侧和点M与点A在边BC同侧这个条件确定。当符合这个条件时，则判断点M在三角形ABC内。因为叉乘可以判断一个点在直线的那一侧，本文通过叉乘计算对3个条件进行判断。对应叉乘公式为

(7)

从图7仿真结果可以看到通过叉乘能够准确判断出位置点是否在三角形正样本区域内，此方法能够作为三角形交通标志正样本区域内位置点的选取方法。

图7 仿真结果

改进后的FCOS算法正标签选择策略是将提出的真实框收缩正样本选择策略与原算法中Center-ness策略相结合，共同提取高质量正样本标签。其中三角形形状特点的交通标志目标特征点不是原来的真实框中心点，所有Center-ness需要重新计算。计算方法与原算法保持一致，只是改变了特征中心点位置，三角形交通标志计算Center-ness公式为

(8)

式中：4个值l*，r*，t*，b*， 分别表示目标框内回归位置点离矩形框左边、右边、上边、下边的距离。Δα表示三角形交通标志目标特征中心点到真实框中心点的距离。

圆形交通标志和三角形交通标志在改进算法后的Center-ness值仿真结果图如图8所示，从图中得Center-ness的大小与检测目标特征中心值相关，当位置点与特征点重合时最大，然后随位置点到特征中心点的位置距离线性减小。

图8 圆形和三角形交通标志Centerness值仿真对比

3 实 验

本文算法使用小目标占多数的TT100K交通标志数据集进行训练预测。该数据集是由腾讯公司发布，平均尺寸为2048×2048，该数据集统计得到大多数目标尺寸都是在16-60像数点之内，对目标的检测模型要求很高。该数据集的训练集的图片有6105张，测试集图片有3071张。按照上文提到的交通标志的分类规则，将该数据集目标为3类：Prohibitory、Mandatory和Danger进行标注。对应的目标数量分布图为图9。

图9 数据集目标分布

实验平台硬件配备了两个TITANXp GPU(显存大小20 GB)，Intel(R)Core(TM)i7-7800X CPU，32 GB RAM；软件搭建Ubuntu16.04 操作系统，Python3.6，以下实验训练测试全部是在该平台上完成。实验训练过程中，使用PyTorch框架对不同算法网络模型进行搭建，特征提取网络ResNet50[15]初始权重在ImageNet上预训练得到。训练超参数设置，见表1。

3.1 结果评价指标

本文使用目标检测常见的精度评价指标mAP(mean average precision)对实验结构进行分析。由于mAP是数据集中所有类别AP值求平均，所以要计算mAP，首先得知道某一类别的AP值怎么求。不同数据集的某类别的AP计算方法大同小异，主要分为3种，本文将VOC2010及以后的方法作为评价标准，根据每一个不同的Recall值选择Precision值，然后根据PR曲线计算AP值。数据集中每张图片中这一类别的Precision和Recall由下列公式计算

(9)

式中：TP表示准确检测出的正样本，FP表示检测失败的正样本，FN表示检测错误的负样本。

平均精度AP近似等于精确率和召回率曲线下面积，计算公式为

(10)

式中：p(k) 对应召回率在k点对应的精确率，指任何召回率在大于k点时的最大准确率。 Δr(k) 表示k点变化时对应召回率的变化量。N表示检索出的目标集数目。不同类别的AP分开计算，i表示不同类别的索引值。

3.2 实验结果和分析

实验首先为确定改进算法选择正标签的最佳的收缩因子，将原正样本收缩算法与新设计的结合交通标志形状特点的正样本策略分别进行消融实验，确定最佳收缩因子后，然后与原算法进行实验对比，最后对预测结果进行非极大值抑制(NMS)[17]分析，验证新的正样本选择策略的有效性。

为确定改进后正标签策略的最佳正标签的收缩因子，首先做消融实验，将结果最好的正标签的收缩因子确定为最佳收缩因子。实验中，通过将真实框宽度和高度乘以一个收缩因子来调整正样本区域的大小。在相同的实验环境下，分别对收缩因子1.0、0.8、0.6和0.4做实验，其它参数保持一致。性能结果见表2。

表2 不同收缩因子消融实验

从表2不同收缩因子对比实验结果得到，收缩因子减少到0.8，检测精度提高，验证了一些远离目标中心的正标签的消除对算法的训练有好处，即远离目标中心的正标签训练时会引入噪声，影响检验精度。将新的融合交通标志形状的正标签选择策略与原收缩策略检测对比，得到融合交通标志正标签选择策略性能更好，当收缩因子为0.8时，mAP最高达到83.2%，验证了融合交通标志正标签选择策略的合理性。由上述实验确定了最佳收缩因子为0.8，下面的对比实验中将收缩因子设置为0.8。

确定收缩因子为0.8后，从损失函数值的变化进一步分析使用交通标志形状特点的正样本标签选择对改进算法的性能提升的原因。从图10的损失函数图看出，使用改进后融合交通标志形状特点的正样本选择策略去除大量噪声正样本标签，损失曲线收敛更快，拟合效果更好。

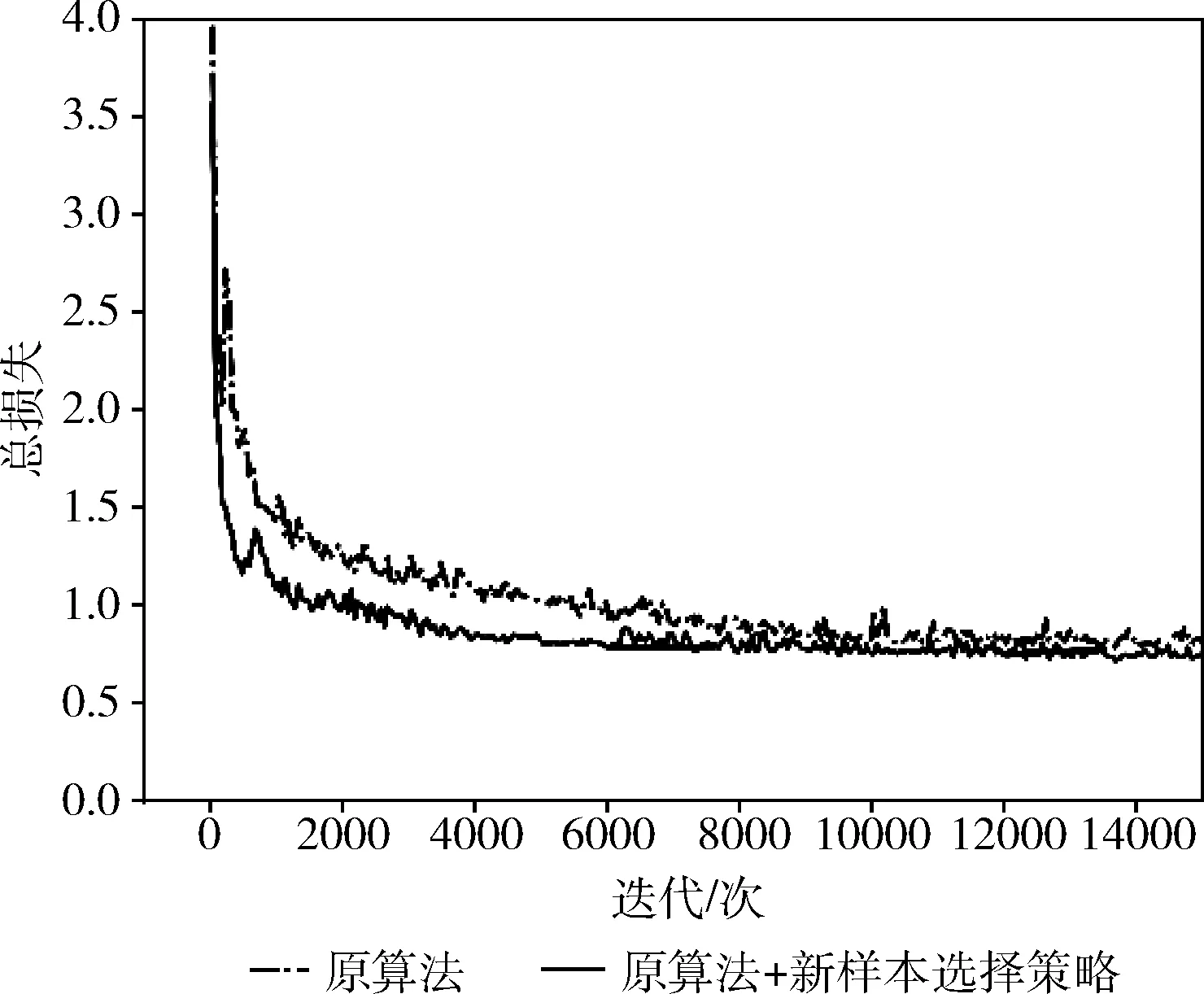
图10 损失曲线对比

与原算法进行对比实验，对比结果表3中得到对算法应用改进后的正样本标签策略后检测精度得到提升，由于Danger类中交通标志三角形形状居多，训练时改变了目标特征中心点位置，相比其它类检测精度提升最大，进而分析得到并不是每一个样本都有助于损失函数进行计算训练，因为正标签中的一些样本可能是完全错误的或者质量很差，造成训练干扰。由于交通标志目标小形状类似并且只有标志的中心位置附近具有分辨信息，在训练过程中注入了大量的标签噪声，影响最后的检测精度。实验验证了新的正样本选择策略能有效去除噪声标签，有助于交通标志的检测识别，提高检测器性能。与其它算法实验结果对比见表4。

表3 实验结果对比

表4 与其它算法实验结果对比

由上表实验结果可以看出，在数据集的3种类别Prohibitory、Mandatory和Danger上与其它检测算法对比，改进后的算法精度上优势明显。最后对上面实验结果综合分析得到，本文对FCOS算法正标签选择策略进行改进，改进后的正标签的选择策略对原算法的检测精度提高明显，与其它算法相比，在交通标志数据集TT100K中，该算法对交通标志检测效果性能上有很大提高，由表5检测速度结果对比得出改进后与其它算法检测速度相差不大，分析改进后算法如图11实验效果图得到改进后算法可以较好检测出交通标志目标。

4 结束语

为获得更高质量的正样本标签对交通标志进行检测识别，分析得到基于anchor-free正样本位置点的选取并不是根据目标特征中心点，而是直接将真实框的中心点作为特征中心点。基于交通标志独特的形状特点，圆形、三角形和正方形等，设计新的正样本选择策略，更好去除噪声标签、低质量标签并且选择更加合理的特征中心，实验验证其有效性。提出的基于交通标志形状特点的正样本标签选择，虽然能够进一步提高正样本标签的质量，但是基于交通标志独特的特点来确定检测目标的特征中心点，遇到特征中心点没有规律的检测图像，如何设计算法准确预测目标特征中心点，选择高质量正样本标签是下一步研究的关键。