基于改进有效信噪比的混合自动重传请求算法

刘庆利，曹 娜，李梦倩，王美恩，商佳乐

(大连大学 通信与网络重点实验室，辽宁 大连 116622)

0 引 言

卫星的空间通信具有长时延、高误码、间断性的特点[1]。为了克服卫星通信的缺陷，降低卫星通信高误码率所带来的影响，高级在轨系统(advanced orbiting system，AOS)引入差错控制技术来保证系统的数据传输，然而引入差错控制技术虽然能保证数据的传输，却牺牲了系统的时延和传输效率。

混合自动重传请求(hybrid automatic repeat request，HARQ)是差错控制技术的一种，这种方法虽然降低了误码率，但同时也牺牲了信道编码的码率导致系统的传输效率也随之降低。近年来，为了改善传统HARQ的缺陷，国内外学者对HARQ进行了深入的研究，文献[2]提出一种安全可靠的认知混合自动重传请求方案，通过隐藏马尔可夫模型(hidden Markov model，HMM)对主用户信道进行建模，但无法精确表示信道的特性。文献[3]建立了基于HAQR重传机制的AMC散射通信模型，阐述了3种HARQ传输机制的特点。文献[4]提出了通过机器学习技术增强的早期混合重传请求的反馈方案，通过使用机器学习的方法来在传输结束之前预测解码过程的结果，体现出了机器学习方案的优势。文献[5]分析了车联网中基于有效信噪比的HARQ的信道增益监测系统性能研究。虽然上述文献降低了无线传输过程的误码率，但因AOS系统长时延、间断性的特点导致的传输过程中的信道状态难以获取的问题还没有得到解决。

为了进一步保证AOS系统误码率的同时提升无线传输过程的吞吐率和降低AOS系统的重传次数，本文提出一种基于改进有效信噪比(improve effective SNR，IESNR)的HARQ算法，联合LSTM和HMM构建混合模型，预测信道传输过程中信道状态的变化趋势，结合LSTM改善HMM预测过程中受时延影响的缺陷，减少冗余的预测步骤，根据预测不同时刻的ESNR动态调节汉明码监督码元数量，通过调整信道编码的码率进而提高AOS系统数据传输效率，降低系统的重传次数。

1 无线信道ESNR预测模型

1.1 LSTM和HMM混合预测模型

在无线通信系统中，一般会采用交织和扩频技术来削弱发送数据之间的关联性，那么这样的无线通信的衰落信道可以被认为是没有记忆的。然而，现在无线通信的数据传输效率越来越高，相邻数据帧之间的关联性就不可忽视了。由于HMM可以很好描述信道的记忆性，可以采用HMM来对有记忆性的无线信道进行建模。在AOS中，很多系统状态是难以观测的，因此，需要将原来难以捕捉的信道状态由可以产生可观测序列的随机过程来描述，这种可观测序列由HMM的隐含状态决定，本文以ESNR为HMM的观测序列。

HMM是通过观测序列上一时刻的隐含状态迭代计算预测出下一时刻的隐含状态，然而，若信道的突发错误较长时，由于HMM通过反复迭代来计算数据的丢包情况，会导致数据传输的延迟增大。因此，如果将HMM的状态转移和LSTM联系起来，将LSTM的输出作为预测结果，则利用LSTM可以改善HMM信道长时依赖的特性，通过将HMM的反复迭代进行预测的过程交由LSTM完成，减少HMM冗余的预测过程。因此，需要建立联合HMM和LSTM的混合预测模型。LSTM-HMM预测过程如图1所示。

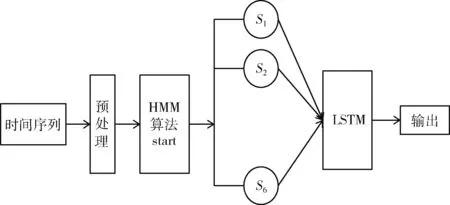
图1 LSTM-HMM预测过程

上述组合模型的整个流程可以分为两个阶段，第一阶段使用HMM算法将AOS通信链路状态划分为不同的状态序列集；第二阶段对每个状态分别使用LSTM模型进行处理，最终输出预测结果。针对HMM对AOS链路的不同状态的LSTM模型学习有如下优势：

(1)相同状态的输入数据具有一定的相似性，有助于模型的收敛。

(2)针对下一时刻的预测，可以使用HMM进行状态概率估计结合LSTM模型预测，充分发挥二者的可解释性和高精度优势。其中不同阶段的算法和模型的细节实现会在后面分别介绍。

HMM可分别由以下5种元素来表示：

(1)隐含状态S，它的状态集合可表示为S={S1，S2，…，S6}， 表示AOS系统的通信链路在某一时刻的信道状态。二状态的HMM模型如图2所示。

图2 二状态HMM模型

(2)观测序列O，观测序列集合可表示为O={O1，O2，…，OM}。 观测序列表示AOS通信链路的传输情况。

(3)状态转移矩阵A，可表示为A={aij}N*N， 其中aij=p{qt+1=Sj|qt=Si}，1≤i，j≤N， 即表示AOS系统通信链路的信道状态从Si变化为Sj。

(4)观测序列分布矩阵B={bjk}N*M， 其中bjk={Ok|qt=Sj}，1≤j≤N，1≤k≤M， 即表示AOS系统通信链路在信道状态为状态Sj时，其对应的观测序列Ok的概率。

(5)初始状态分布D，D={Di}， 其中，Di={q1=Si}，1≤i≤N， 即表示信道的初始状态为Si。

因此，一个完整的HMM模型可以由隐含状态、观测序列、初始状态决定。可以使用λ=(A，B，D) 来表示完整的HMM模型，HMM如图3所示。

图3 HMM

其中，HMM的状态S除了能从一个状态转移到其它状态，也有可能从自身转移到自身。例如：某一时刻的状态为S2， 可能下一时刻的状态是S5或者是S2。 具体的HMM状态转移过程如图4所示。

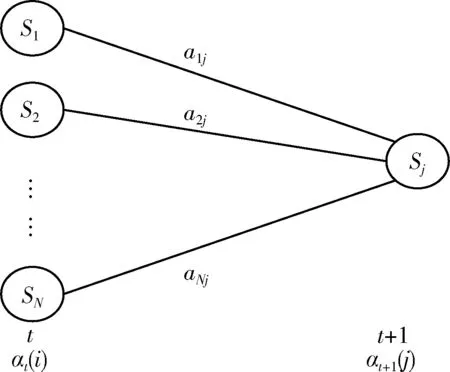
图4 HMM状态转移

其中，Sj表示HMM的隐含状态即AOS链路的信道状态，aij表示从状态i转移到状态j的转移向量即信道状态的变化，αt(i) 是HMM预测过程中前向变量，Ok表示HMM的观测序列。如图4所示，AOS系统的通信链路的信道状态在t时刻可能为S1至SN中的某一个，到下一个时刻t+1，可能从t时刻的Si变化为Sj。 使用HMM算法根据系统的通信链路的初始信道状态以最高信道状态的转移概率P(O|λ) 为原则求解信道状态的变化关系。将原HMM的训练序列状态作为LSTM的输入层，则可以将原先由HMM通过迭代计算来完成的预测过程交由LSTM来完成，以改善HMM长时依赖的缺陷。

有效信噪比，即系统的接收端数据的单位比特的能量和系统通信链路的信道的噪声功率密度的比值[6]。相比于传统信噪比，有效信噪比更真实地反映了为达到目标误码率AOS信道所需的实际能耗情况。设L表示AOS通信系统通过混合自动重传请求成功接收一个码字的传输次数，则E[L] 可以表示系统数据传输的平均传输次数，将其定义为AOS通信系统发送码字的次数与接收端接收码字的次数的比值。假设AOS系统的数据在传输过程成功传输的概率为p。 则成功接收一个码字所需平均传输次数[7]为

(1)

由式(1)可知，系统在传输数据过程中的平均传输次数与其成功传输一次的概率p存在反比关系。那么，在设置系统的最高重传次数为M的情况下，E[L] 可如下式表示

(2)

从式(2)中可以看出，AOS系统成功接收一个码字所需的平均传输次数与重传次数的上限M无关，仅与接收概率p有关。而瑞利衰落信道下的信噪比

(3)

(4)

LSTM采用了LSTM层替代传统的隐藏层，并且拥有3个门：输入门、遗忘门和输出门，这使得LSTM可以更好地处理长时依赖的问题。LSTM网络结构如图5所示。

如图5所示，从左到右依次为LSTM的遗忘门、输入门、输出门。故整个LSTM可以分为以下3步。

(1)计算遗忘门的输出值

ft=σ(wf[ht-1，xt]+bf)

(5)

(2)计算输入门的值

it=σ(wi[ht-1，xt]+bi)

(6)

c′t=σ(wc[ht-1，xt]+bc)

(7)

ct=ft⊗ct-1+it⊗c′t

(8)

(3)计算输出门的值

ot=σ(wo[ht-1，xt]+bo)

(9)

ht=ot⊗tanh(ct)

(10)

其中，wf，wi，wc，wo分别是遗忘门、输入门、细胞状态和输出门的权重矩阵，bf，bi，bc，bo分别为遗忘门、输入门、细胞状态和输出门的偏置项。c′t为LSTM在t时刻数据的处理状态，ht为t时刻的LSTM神经网络的输出，σ为sigmoid激活函数，xt为t时刻的输入，tanh为双曲正切函数，⊗表示矩阵元素相乘。

1.2 混合预测模型对ESNR的预测

采用六状态的HMM来描述AOS系统的通信链路的信道状态的变化情况，并根据系统信道的SNR将AOS系统的信道状态划分S1至S6。具体的隐含状态与SNR对应关系见表1。

表1 隐含状态与SNR对应关系

在混合预测模型中，可以直接将ESNR与观测符号联系起来，减少冗余的预测步骤。假设HMM的观测符号序列O={O1，O2，…O15，O16}。 首先初始化样本得到最初的初始化状态S1，固定的状态序列为Q=q1q2…qt。 则AOS系统的ESNR的观测序列O的传输概率可以通过上述的状态变化关系求解，具体如下式所示

(11)

对于上述公式，初始时刻的状态为q1， 概率为πq1， 并且以概率bq1(o1) 产生观测符号O1， 到下一时刻时，状态q1以aq1q2的概率转换为q2， 并且状态q2产生观测符号O2的概率为bq2(o2)， 依此类推，直至最后一刻qt为止。

定义前向变量如下式所示

αt(i)=p(o1o2…ot，qt=Si|λ)

(12)

αt表示的是从开始到t时刻，观测序列为O1O2…Ot的概率，将其作为LSTM的输入。则上述式子可以如下所示

(13)

基于LSTM-HMM的混合预测模型的主要流程可以分为两个阶段，分别为两个训练流程以及预测流程。首先通过初始化HMM参数λ， 结合观测序列O，得到隐藏状态序列S和状态概率转移矩阵A，最后通过HMM求解AOS通信链路的传输概率p。然后根据HMM对信道状态的划分情况，结合LSTM对AOS通信链路的SNR进行预测，最后根据LSTM的预测结果进而实现对AOS通信链路的ESNR的预测。预测效果如下所示：

本文以LSTM和HMM的混合模型为基础对通信链路的ESNR状态变化进行预测，整个过程分为两步进行，首先利用HMM求解系统的传输概率，然后通过SNR的数据集对LSTM进行训练。最后，与只使用LSTM预测的结果进行对比。由于只考虑对通信链路的ESNR这一个特征进行处理，因此设置LSTM网络选择rmsprop作为预测优化器，以均方误差MSE为损失函数。其中网络结构为3层，隐藏层单元数为32，dropout为0.2，通过python的kears完成编译仿真过程。采用长度为40 500时间戳的数据，横轴为ESNR的条数，纵轴为ESNR，前12 000个数据作为测试集，后28 500个数据作为训练集。LSTM-HMM混合模型在预测ESNR的性能方面的对比如图6所示。

从图6中可以看出，随着SNR不断变化，得出LSTM-HMM在预测中表现略优于只使用LSTM的预测效果。但由于数据波动幅度大，看不清其中细节。为分析所提算法的预测性能，放大预测结果中3600到5000时间戳的数据如图7所示。在图7中，LSTM-HMM在面对快速下降的信道状态，所预测结果更符合现实情况。这是因为在时间戳4200到4500期间的预测结果使用时间戳3600到3900期间数据训练的网络，而时间戳3600到3900期间的SNR波动很大。当使用3900到4200时间戳中数据进行训练网络时，预测结果在时间戳4500到4800期间有所改善。在整个期间，因为HMM预先对信道状态的进行划分，然后再使用LSTM对SNR进行预测，最后，根据预测的结果得到ESNR，因而预测结果大幅提升。由此可以得出LSTM预测模型不能应变复杂、多变的信道状态，而LSTM-HMM混合模型预测出的ESNR的变化趋势是吻合通信链路的ESNR的变化趋势的，因此，系统可以根据混合模型的预测值来进行下一步操作。

图7 ESNR的预测效果放大

2 基于改进ESNR预测的混合自动请求算法

ESNR表示在整个重传过程中对系统的通信链路的传输能力的间接表现，ESNR的变化的同时也反映出了信道状态的变化。基于IESNR的HARQ算法通过融合HMM和LSTM所组成的混合预测模型，预测系统数据在传输过程中的链路信道的ESNR变化关系以此来调整系统的信道编码的纠错能力，进而从整体上提升系统的传输性能。以汉明码为例，对于汉明码，r个监督元，可以传输m+r+1位数据，其中m是指传输的信息位数，具体如下式所示

2r≥m+r+1

(14)

第t秒与第t+1秒观测符号比值为

(15)

如果δ的值逐渐减小，说明系统的ESNR在逐渐降低，表明数据重传的开销在增加，信道状态正在恶化，则此时可以适度增加监督码元的数量以求增加系统的可靠传输。反之，如果δ增大，则说明信道的状态正在改善，则此时应该适度增加信息码元的数量以求数据的传输效率。假设t秒时汉明码监督元数量为ut， 则t+1秒时汉明码监督元数量为

(16)

设定最大及最小监督元数目，如果ut+1超过最大监督元数目，则以最大监督元数目作为编码方案，如果ut+1小于最小监督元数目则以最小监督元数目作为编码方案。同时，设定最大传输次数，若接收端译码失败，则由反馈信道传输否定信号，编码器下一次传输则增加一定量的监督元数目。此时，如果监督元数量超过上限，则采用最大监督元数目方案。

基于IESNR的HARQ算法具体步骤如下。

(1)由系统的通信链路的初始信道状态对HMM进行初始化并得到对应参数，将系统的通信链路的传输情况变化关系所构成的时间序列作为观测序列O，通过过去时间段内的前向变量αt得到观测序列o1o2…ot的样本，结合状态转移矩阵A求解系统的传输概率P。

(2)在系统此时刻的信道状态为Sj的条件下，通过过去一段时间的SNR的变化数据的训练，利用LSTM预测下一个时刻的信道的ESNR的变化趋势。

(3)根据预测的ESNR变化趋势调整汉明码的校验位并完成数据的传输过程。

(4)系统的接收端进行译码并判断译码是否成功，若译码成功则继续传输。若译码失败则系统进行重传，并重复执行以上步骤，继续判断译码是否成功，如果不成功且系统的重传次数没有达到上限值，则系统继续重传该数据。如果在传输过程中，监督码元的数量超过其上限值或低于其下限值，则以监督码元的上限值或下限值为准。

IESNR算法的流程如图8所示。

图8 IESNR算法流程

3 实验结果与分析

3.1 仿真参数设置

本文通过matlab仿真软件，搭建仿真系统，对提出的基于改进ESNR预测的混合自动重传请求算法进行仿真验证并与其它两种HARQ算法进行对比，其具体仿真参数设置见表2。

表2 仿真参数设置

3.2 仿真结果分析

利用matlab仿真工具对该算法进行仿真，并与II型HARQ算法，基于ESNR的HARQ算法进行比较。编码方式采用汉明码，调制采用bpsk，信道采用瑞利信道。关于3种HARQ算法的误码率对比如图9所示。

图9 3种HARQ算法误码率仿真对比

由图9可知，由于最初信道的SNR很低，即此时系统的通信链路的信道状态并不适合传输数据，故此时3种HARQ算法的误码率都较高，随着SNR的增加即信道条件的改善，3种HARQ的算法的误码率整体上呈降低趋势。但是由于基于改进ESNR的HARQ算法可以通过预测信道的ESNR变化调整信道编码的监督码元，强化其纠错能力，所以整体上，II型HARQ算法的误码率最高，基于ESNR的HARQ算法其次，基于IESNR的HARQ算法的误码率最低，表明了相较于前两种HARQ算法，基于IESNR的HARQ算法降低了系统的误码率。

为了验证基于IESNR的HARQ算法在传输过程中的传输效率，与II型HARQ算法、基于ESNR的HARQ算法在传输次数的对比如图10所示。

图10 3种HARQ算法传输次数仿真对比

由图10可知，在最初的SNR较低的情况下，即此时的信道的数据传输发生错误的可能性较高，此时在系统的接收端进行译码时，由于超出HARQ的纠错能力，故此时只能选择重传来确保数据传输，因此3种HARQ算法的传输次数都较高，随着信道状态朝着利于数据传输的方向的不断变化，在传输过程中发生错误的可能性也随之逐步降低，故3种HARQ算法的传输次数也随之降低，当信道的SNR高于10 dB时，此时的信道的传输状况良好，数据传输时发生错误的概率已经较低且接收端在译码时通过HARQ能够完成自我纠错，此时不需要通过重传来保证数据传输，因此，传输次数将较低。在整体趋势上，3种HARQ降低系统数据传输的能力各不相同，其中II型HARQ能力较差，其次是基于ESNR的HARQ算法，由于基于IESNR的HARQ算法通过预测可以及时调整传输过程中的码率，故相较于其它两种HARQ算法，有效降低了系统的传输次数。

吞吐率为AOS接收端接收且译码成功的比特数与AOS发送端发送的比特数的总值相比，因而能反映系统传输效率。基于IESNR的HARQ算法与II型HARQ算法、基于ESNR的HARQ算法在吞吐率的对比如图11所示。

图11 3种HARQ算法吞吐率仿真对比

由图11可知，随着信道状况的不断改善，3种HARQ算法的传输的吞吐率也会随之不断增加，然而，从整体趋势可以发现，基于IESNR的HARQ算法传输数据的能力要优于其余两种HARQ算法，表明，相较于其余的两种HARQ算法，基于IESNR的HARQ算法提升了数据传输效率。

4 结束语

针对传统的HARQ在传输过程中保证AOS系统数据传输的同时也带来了传输时延的问题，本文提出了一种基于IESNR的HARQ算法。该算法在基于ESNR的HARQ算法的基础上，结合LSTM和HMM改进引入HARQ所带来的低传输效率的问题，根据不同时刻ESNR的比值关系动态调节汉明码的监督元数量。仿真结果表明，在改进预测结构的基础上，通过自适应调节汉明码编码冗余量，能够达到降低系统误码率的效果，同时也有效地降低系统的传输次数，提高了系统的吞吐率。