融合多维属性相似度的云制造服务谱聚类算法

黄 雯，胡 强，任志考

(青岛科技大学 信息科学技术学院，山东 青岛 266061)

0 引 言

随着云计算、大数据等新一代信息技术与先进制造技术的融合，云制造作为一种新的模式应运而生[1]。在云制造环境下，资源提供方将自身拥有的加工设备资源或制造能力通过虚拟化、服务化的方式发布到云制造平台[2]。用户可以在平台中寻找所需要的云制造服务，通过租用这些云制造服务来实现超出自身制造能力的业务需求，以一种低成本代价的方式弥补业务制造能力的不足，从而提高企业竞争力。

相比普通云服务，云制造服务的属性参数数量更多，参数的取值类型较为丰富，不仅有短文本类型的功能描述，也有数值型的工艺属性参数。在同一类云制造服务中，不同属性的取值通常也会跨越多个数量级。在查找云制造服务时，不仅要考虑服务的功能描述，也要同时兼顾制造工艺参数属性值的约束，因此，从大量功能相似的云制造服务中发现适合用户需求的云制造服务难度大、效率低。

服务聚类可将服务按照功能的相似性划分为若干个簇，缩减搜索空间，有效提高服务查找速度[3]。目前，直接以云制造服务作为聚类对象相关研究成果仍然较少，有关工作主要关注制造设备或资源的聚类，例如，高新勤等对k-means算法进行改进，提出了基于相似度的加工设备云服务聚类方法，利用可拓论建立了服务请求与云服务类簇的物元模型，实现服务供给与服务请求的快速匹配[4]。辜振谱等将马氏距离引入到密度峰值聚类算法的密度中心测定中，基于改进密度峰值聚类算法实现航空发动机故障诊断，所提出算法在故障特征的分类与识别上均优于K均值聚类和模糊C均值聚类[5]。郝予实等提出基于场景识别的云制造服务推荐模型，该模型重构服务组合描述的功能信息，对服务组合进行应用场景的服务聚类，为各场景建立加权库进行服务推荐，该方法在推荐效果上有很大提升[6]。

以K-means++、层次聚类等为代表的聚类方法因实现简单且聚类效果良好而得到广泛应用，但这些方法多适用于线性分布的数据样本空间。云制造服务存在多个维度的功能和属性特征描述，且这些特征描述所采用的数据类型种类较多，数据取值差异大，因此，云制造服务在聚类时构成非线性数据样本空间，上述聚类算法在对云制造服务聚类时效果不理想，算法容易陷入局部最优。为了更高质量地实现云制造服务聚类，选取能够识别任意形状样本空间且能快速收敛于全局最优解的谱聚类算法作为云制造服务聚类算法。

为了充分利用云制造服务所拥有的多维属性约束信息来提高聚类质量，本文提出一种基于改进谱聚类的云制造服务聚类算法。针对文本型和数值型服务属性参数，分别构建相似度计算方法，并提出一种适用于文本型和数值型相似度矩阵融合函数，实现云制造服务多维属性相似度的融合计算，引入服务相似矩阵的本征间隙确定聚类个数，提高谱聚类的聚类数量确定的合理性，进而实现高质量的云制造服务聚类。

1 云制造服务的相似度计算

云制造服务S定义为三元组S={n，SF，SQ}， 其中，n为服务的名称，SF表示服务的功能属性集合，SQ表示服务的非功能属性集合。

不同类型的云制造服务在工艺流程、制造参数和性能上存在差异，难以统一给出SF和SQ的具体属性参数组成，通常情况下，有关工艺流程和制造参数方面的属性在SF中刻画，SQ则由云制造服务性能层面的属性组成，以某服务商提供的轮胎结构加工服务为例，SF和SQ的构成参数见表1。

表1 轮胎结构加工服务信息

1.1 文本型属性相似度计算

云制造服务描述中，各类属性的取值通常可以划分为文本型和数值型两类。文本型属性主要包含加工对象、功能描述、类别、隶属行业、材质等信息的描述，这些属性值中既有段落级别的短文本，也有单个名词或词组。为精确地获取服务的功能语义，本文采用GSDMM对段落级短文本信息提取主题向量，对于单个名词或词组，则采用Word2Vec生成对应的文本向量，然后利用上述向量求解对应属性的相似度，将所有文本型属性相似度的平均值作为两个服务之间的文本型属性的最终相似度。

对于属性值为单词或组词的文本属性，利用Word2vec生成词向量。Word2vec分为两种模型：CBOW和Skip-Gram，本文采用Skip-Gram模型，Skip-Gram模型是通过特定词来预测上下文，生成词向量[7]。Skip-Gram模型定义词出现概率p(wo|wc)， 其计算方法参见式(1)

(1)

式中：wo，wc分别代表上下文词和中心词，vc表示中心词的词向量，uo代表上下文词的词向量，ui表示除中心词以外第i个单词的词向量，V表示全体词库。Skip-Gram模型训练函数如式(2)所示

(2)

此处，c是上下文窗口大小。

对于段落级别短文本描述的属性值，采用GSDMM生成描述文本的主题向量。GSDMM模型是一种无监督主题概率模型，该模型基于狄利克雷混合模型(DMM)生成文档，然后采用吉布斯采样(Gibbs Sampling)求解模型[8]，能够快速获取文本集中每个文本的潜在主题。GSDMM模型中由文档得到主题的概率为式(3)

(3)

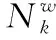
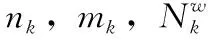
(3)对文档集中的所有文档初始化完成后，得到K个属于不同主题的集合，且每个文档只属于一个主题。

(5)重复步骤(4)，直到i大于最大迭代次数。

在为段落级文本属性值生成向量时，首先借助Python工具包对文本进行分词、去停用词、还原词干等操作，通过GSDMM为每个段落级别的短文本属性值生成一个主题向量。再利用Word2Vec和GSDMM将全部文本类型的属性值生成对应的向量后，可通过余弦夹角公式计算两个服务对应属性文本值之间的相似度，两个服务最终的文本属性值相似度定义为所有服务所有文本属性值相似度的均值，具体参见定义1。

定义1TA={t1，t2，…，tn} 和VTA={vt1，vt2，…，vtn} 分别是云制造服务si和sj的文本属性集合与属性值对应的文本向量集合，即∀ti∈TA，vti为ti对应的属性文本值生成的向量，si和sj的文本属性值相似度定义为

(4)

表2给出5个云制造服务的文本型属性，在依据文本类型的属性值生成对应的向量后，参考定义1计算两个服务的文本型属性相似度，构建了云制造服务的文本型相似度矩阵SM_T

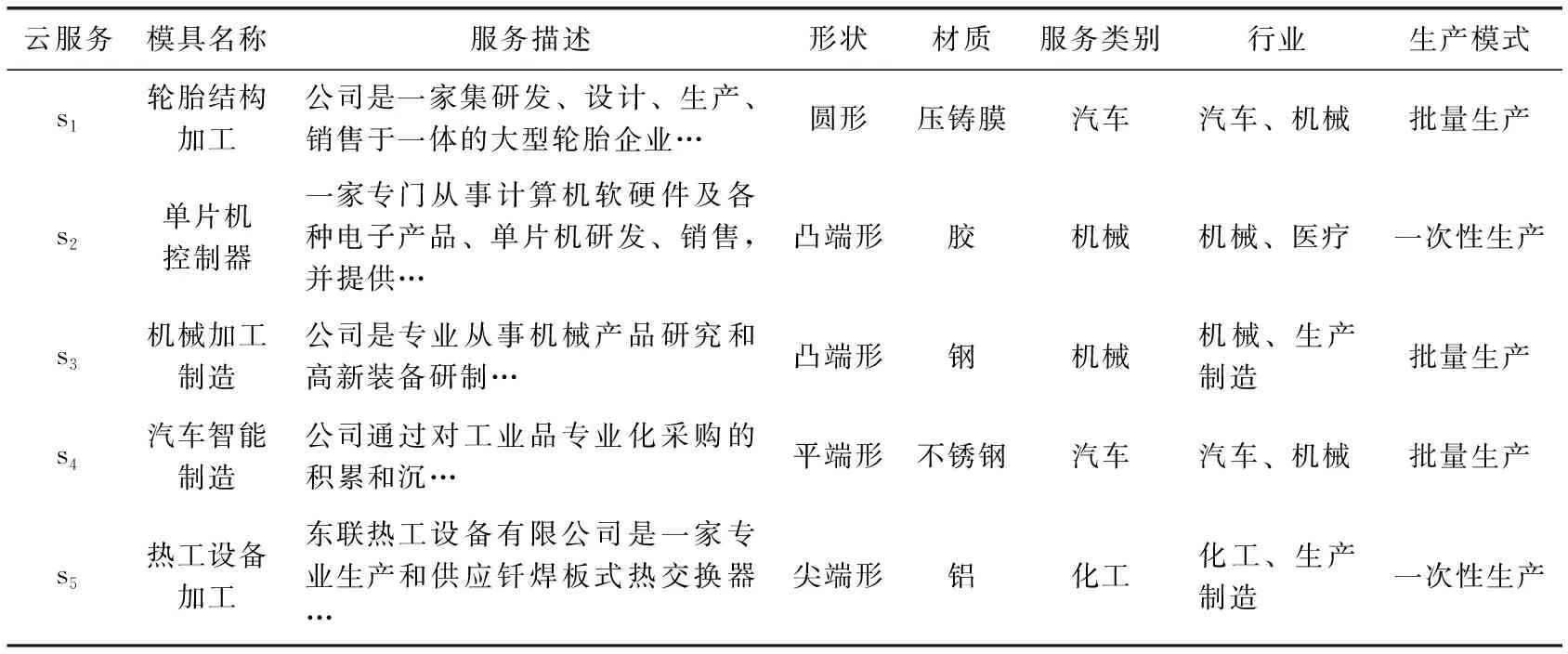
表2 云制造服务文本型属性信息

1.2 数值型属性相似度计算

表3给出表2中5个云制造服务所对应的数值型属性，为了能够使用这些参数进行服务聚类，首先对这些参数按照类别采用“最大-最小标准化”方式进行归一化。归一化后的各个属性参数值均在区间[0，1]内，两个服务的数值型属性相似度计算方法参见定义2。

表3 云制造服务数值型属性信息

定义2si和sj是一组云制造服务中的两个服务，NA={t1，t2，…，tn} 和NNA={nt1，nt2，…，ntn} 分别是服务si和sj的数值型属性集合与属性值对应的归一化数值集合，即∀ti∈NA，nti为ti对应的归一化后的属性值，si和sj的数值型属性值相似度定义为

(5)

从定义2可知，两个服务的数值型属性之间的相似度通过融合幂指函数的欧式距离计算得到。在计算时，首先将属性值进行了归一化，然后将归一化后的属性值作为样本数据，利用欧式距离公式计算两个服务的欧式距离。由于欧氏距离的值越小，样本数据越相似，因此引入幂指函数将欧式距离正向映射为服务之间的数值型属性相似度。

利用表3中的5个服务的数值型属性，构建了服务s1～s5的服务-数值型属性矩阵(SNA_M)，将其归一化后可得矩阵SNA_NM，利用定义2可以计算获得服务s1～s5的数值型属性相似度矩阵SM_N

1.3 云制造服务相似度计算

为了能够使用谱聚类算法对云制造服务进行聚类，需要将云制造服务的文本型属性相似度矩阵SM_T与数值型属性相似度矩阵SM_N进行融合，构建云制造服务相似度矩阵SM。本文构建如式(6)所示的矩阵融合函数实现SM_T与SM_N的融合

(6)

算法1给出了如何求解云制造服务集合中两个服务相似度的算法。第(1)行获取集合S中的服务个数，以及该服务集合中服务的属性数量。算法(2)至(8)行，分别获取服务的每一个属性，通过valtype()函数判定属性的类型。若属性值为短文本类型则采用GSDMM为其训练文本向量，若属性值为单词或词组，则采用Word2Vec生成单词的向量；若属性值为数值型，则对该集合中所有服务进行属性值的归一化。算法第(9)至(14)行用于构建服务的文本型属性相似度矩阵SM_T和数值型服务相似度矩阵SM_N。对于给定服务si和sj，在进行文本型属性相似度和数值型属性相似度计算时，分别采用定义1中的TS(si，sj) 和定义2中的NS(si，sj)。 算法第(15)行利用式(6)实现文本型属性相似度矩阵SM_T和数值型服务相似度矩阵SM_N的融合，最终返回集合S中服务的相似度矩阵SM。

算法1：CAL_ServiceSim

输入：the set of Cloud serviceS

输出：Service similarity matrixSM

(1)m=|S|,n=|S.TA|+|S.NA|;

(2)fori=1 tom

(3)fori=1 ton

(4)ifthe valtype(ti) is a word or phrase, trainvtiby Word2Vec;

(5)ifthe valtype(ti) is short text, trainvtiby GSDMM;

(6)ifthe valtype(ti) is numerical value, normalized it to getnti;

(7)endfor

(8)endfor

(9)fori=1 tom

(10)forj=1 tom

(11) compute theTS(si,sj) and build the similarity matrix for text-type attributesSM_T;

(12) compute the NS(si,sj) and build the similarity matrix for numeric attributesSM_N;

(13)endfor

(14)endfor

(15)generate service similarity matrixSMbased onSM_TandSM_Nby formula (6);

(16)returnSM;

本节为云制造服务中文本型和数值型属性分别建立了相似度计算方法，在此基础上设计了一种多维度属性相似度融合策略，实现了云制造服务相似度的计算，全面有效刻画云制造服务资源间的差异性，从而更精确地实现聚类。

2 基于本征间隙的云制造服务谱聚类算法

谱聚类算法是从谱图划分理论演化而来的，谱聚类算法可以归纳为以下3个步骤：①构造数据集的相似矩阵；②计算矩阵的特征值和特征向量；③利用聚类算法对特征向量进行聚类。

分布式能源行业能效高、低排放、技术密集决定了其投资高，再加上承担园区供热管网建设，以及主要设备燃机属高端制造业，国产化进程有待时日，行业投资高于燃煤发电。

传统的谱聚类算法能够对数据进行较为精确的聚类，但仍有很多不足之处[9]。例如，在第(1)步构造相似矩阵时，通常采用高斯核函数来确定相似矩阵，相关参数需要人为设置，并需反复调试才能确定最优值。在第(3)步中需要人为指定聚类个数，造成聚类数量受人为主观因素影响较大。

针对上述问题，在算法1中提出了一个多维属性相似度计算与融合方法，提出了一种适用于云制造服务的相似度矩阵构建方法，解决了传统高斯核函数在计算云制造服务相似度时的不足。本节引入本征间隙来确定聚类的个数，弥补传统谱聚类算法中人为确定聚类数量的不足。根据矩阵的扰动理论，计算数据之间的本征间隙，自动计算聚类个数。

在云制造服务相似矩阵SM基础上构建度矩阵D，在度矩阵D中，对角线元素的值为相对应行的元素值总和，非对角线元素上的值为0。在度矩阵的基础上参照文献[16]中的式(11)构造规范型拉普拉斯矩阵L

假设规范型拉普拉斯矩阵L存在n个特征值λ=[λ1，λ2…λn]， 对上述求得的特征值按由大到小进行排序，排序后的特征值为λsort=[λ1≥λ2≥…≥λn]， 上述L对应的λ和λsort分别为

λ=[0，0.789 626 48，0.887 051 8，0.858 900 5，0.848 123 38]
λsort=[0.887 051 8，0.858 900 5，0.848 123 38，0.789 626 48，0]

本征间隙序列定义为 {g1，g2，…，gn-1|gi=λi-λi+1}， 在序列中寻找第一个极大值gi，该值的索引i为聚类的个数k[10]

g=[0.028 151 3，0.010 777 12，0.058 496 9，0.789 626 48]

上述序列中第一个极大值为g3，g3-g1>0，g3-g2>0，g3-g4<0，第一个极大值所对应的索引为3，所以聚类个数k为3。在此基础上，构建融合多维属性相似度的云制造服务谱聚类算法，具体参见算法2。

算法2：FMA_SC

输入：Cloud manufacturing service similarity matrixSM；

(1) construct degree matrixDforSM

(2) compute canonical Laplace matrixL

(3) obtain the eigenvalues of normalized Laplacian matrix

(4) sort the eigenvalues byλ1≥λ2≥…≥λn

(5)fori=1 ton-1

(6) compute eigengap sequencegi=λi-λi+1

(7)endfor

(8)fori=1 ton

(9) find the first argmin {gi-gj,j0&gi-gi+1<0}

(10)endfor

(11) assign the number of clusterskasi

(12) calculate the firstkmaximum eigenvectors [Xi,X2,…,Xk]

(13) cluster eigenvectors [Xi,X2,…,Xk] by K-means++

(14) returnkservice clusters

算法2中第(1)行计算云制造服务相似度矩阵SM的度矩阵D。度矩阵D对角线上元素的值D(i，i) 为服务相似度矩阵SM第i行元素之和，其余元素设置为0。第(2)行到第(3)行构建规范拉普拉斯矩阵并计算出该矩阵的特征值。第(4)行将特征值按由大到小进行排序。第(5)行到第(7)行，计算本征间隙序列 {g1，g2，…，gn-1|gi=λi-λi+1}。 第(8)行到第(11)行在本征间隙序列中寻找第一个极大值gi，该值所对应的索引i为聚类的个数k。第(12)行计算前k个特征值对应的特征向量，构造特征向量矩阵。第(13)到第(14)行对向量矩阵采用K-Means++算法进行聚类，得到k个服务类簇。

3 实验与分析

从航天云网、卡奥斯工业互联网平台等知名云服务平台爬取有关制造加工类服务2215条，从中选择1892条数据描述较为完备的云制造服务用于实验验证，实验机器配置采用i7-8750H处理器，Windows10操作系统，16 GB内存，利用PyCharm程序进行编写。采用聚类评价中的常用指标CH、SC、NMI、FMI作为本文服务聚类实验的性能评估指标，相关指标定义参见文献[11]。所有实验均开展10轮次，取所有轮次实验的平均值作为最终聚类效果的对比值[12]。

本文方法FMA-SC对比了4种近年来发表的谱聚类改进算法，在构建的数据集上进行聚类，通过上述4种指标对比算法的性能。

(1)NHASC算法[13]：一种适用于非线性高维数据的谱聚类算法，将数据映射到随机特征空间，把非线性数据映射为非线性数据，然后使用谱聚类算法进行聚类，解决非线性高维数据的聚类问题。

(2)SC_SD算法[14]：一种自适应谱聚类算法，避免样本点的局部尺度参数受噪音点的影响，将样本的邻域标准差作为谱聚类的局部尺度参数，构建服务相似矩阵进行聚类。

(3)SCTSCI算法[15]：提出了一种混合型数据的度量方式，构造尺度参数自适应的核函数来构建相似矩阵，并在谱聚类中运用集成K-means算法增加算法稳定性。

(4)FITS-MSC算法[16]：设计了一种细粒度相似性融合策略来获得最终的一致性亲和矩阵。在融合过程中，探索了局部视图间和全局视图内的权重关系，采用稀疏子空间聚类来构造初始相似矩阵。

图1中的CH指标和图2中SC指标是聚类内部评价指标，从聚类的中心点距离、内部结构凝聚度等层面对服务聚类的质量进行评价。从图1中数据可以看出，本文算法FMA-SC的CH指标得分值显著优于NHASC、SC_SD和FITS-MSC算法，文献[15]中的SCTSCI算法得分值略高于FMA-SC算法。此外，从图2中的数据可以看出，本文方法在SC评价指标获取的分数得到大幅提高，从分值上看，文献[16]中的FITS-MSC算法的得分值最高，略优于本文方法。此外，本文算法SCTSCI性能优于NHASC、SC_SD和STSCI算法，相比其它指标提升幅度均超过40%。因此，从聚类质量的内部评价指标看，本文所提出的FMA-SC方法显著优于已有谱聚类算法。

图1 谱聚类类型算法的CH指标对比

图2 谱聚类类型算法的SC指标对比

图3和图4所示数据对比为聚类外部评价指标NMI和FMI在不同方法中的评分，可以看出本文方法FMA-SC均优于其它方法，相比其它4种方法，本文方法在NMI和FMI性能分别平均提升了约37%和55.8%。

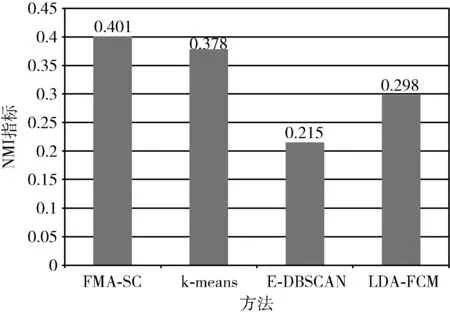
图3 谱聚类类型算法的NMI指标对比

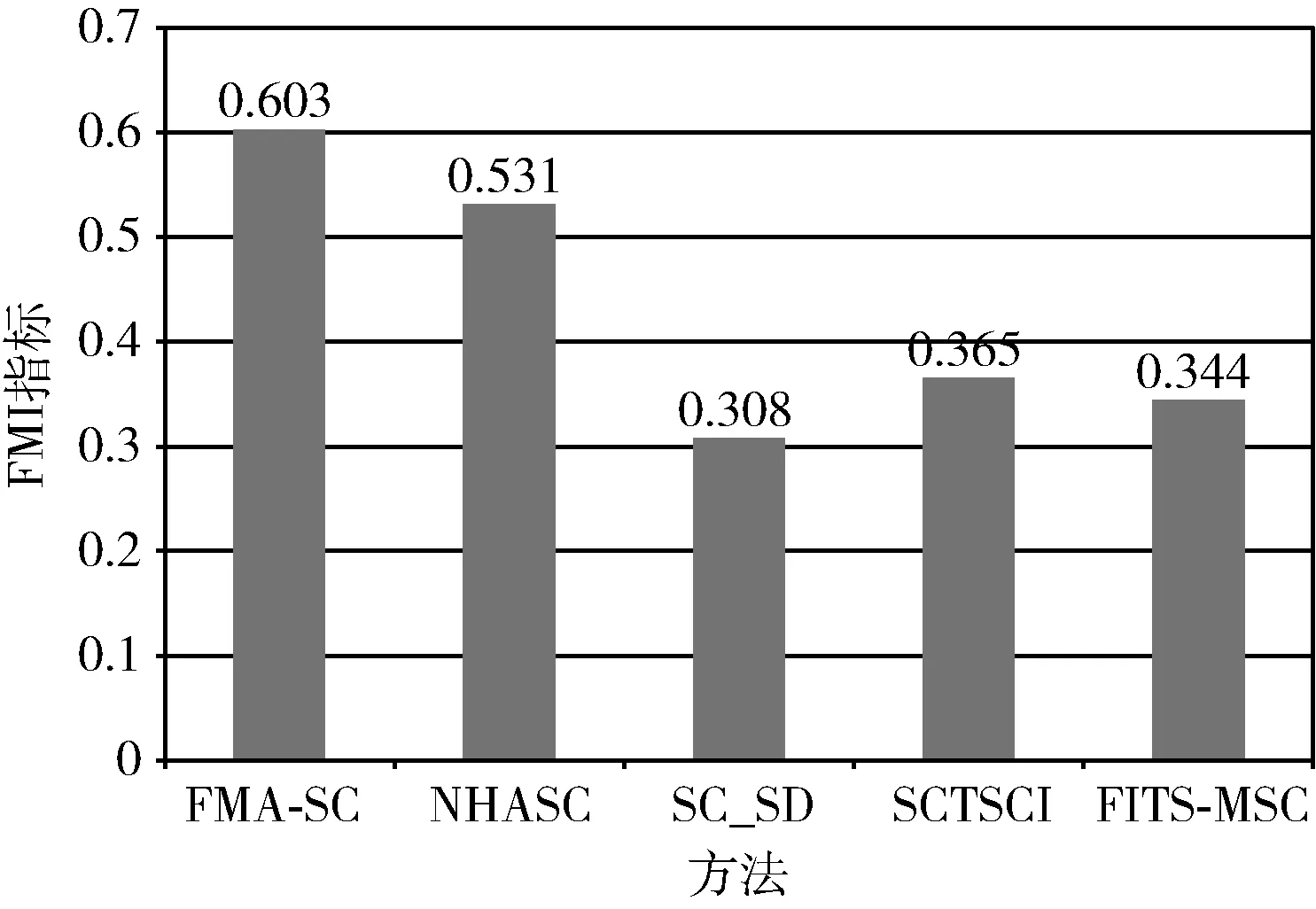
图4 谱聚类类型算法的FMI指标对比

除与改进谱聚类算法进行对比，FMA-SC算法还与其它非谱聚类型算法进行了对比，主要对比算法如下：

(1)K-means算法[4]：该算法对加工设备的制造属性进行描述，改进了K-means算法随机选取初始聚类中心和聚类数目的不足，提出一种基于相似度的加工设备云服务K-means聚类方法。

(2)E-DBSCAN算法[17]：采用LDA-DBSCAN算法进行聚类，首先基于改进的LDA算法挖掘发现隐含数据，提取数据资源特征，解决数据资源无法映射到一个向量空间问题，采用DBSCAN算法进行聚类。

(3)LDA-FCM算法[18]：提出一种基于LDA-FCM方法的Web服务发现聚类方法，该算法使用LDA模型进行Web服务资源数据的重组和自适应调度，以提取web服务数据资源特征，依据数据资源特征确定其相似度，在FCM算法中，通过相似度计算隶属度，实现web服务聚类。

各个指标的对比结果如图5～图8所示。从图5中数据可以看出，本文算法FMA-SC的CH指标得分值显著优于K-means、E-DBSCAN和LDA-FCM算法，在CH评价指标获取的分数得到大幅提高，平均提升了35%。此外，从图6的数据中SC指标可以看出，E-DBSCAN算法的得分值最高，其次是本文FMA-SC算法，FMA-SC算法在SC指标上优于K-means算法和LDA-FCM算法，本文FMA-SC算法与 K-means、E-DBSCAN、LDA-FCM算法相比，在SC性能上平均提升了31%。从聚类质量的内部评价指标看，本文所提出的FMA-SC方法显著优于已有的聚类算法。

图5 非谱聚类类型算法的CH指标对比

图6 非谱聚类类型算法的SC指标对比

从算法运行的时间复杂度来看，NHASC算法时间复杂度为O(n×D)， 其中n为数据个数，D为数据空间维度。SC_SD算法时间复杂度为O(n2)， SCTSCI算法时间复杂度为O(n3)， FITS-MSC算法的时间复杂度为O(t(dmaxn2+n3))，dmax表示数据维度，t表示迭代次数。本文算法FMA-SC的时间复杂度为O(n2)， 在5个算法中并列排名第二，时间复杂度较低。

从图7和图8中的数据可以看出，FMA-SC算法在NMI和FMI指标上均优于K-means、E-DBSCAN、LDA-FCM聚类方法，在NMI和FMI性能上，本文提出的方法与文献[17]中的方法在评分上较为接近。相比于其它3种方法，本文方法在NMI和FMI性能上分别平均提升了31%和36%。因此，从聚类质量的外部评价指标看，本文所提出的FMA-SC方法显著优于已有的其它聚类算法。

图7 非谱聚类类型算法的NMI指标对比

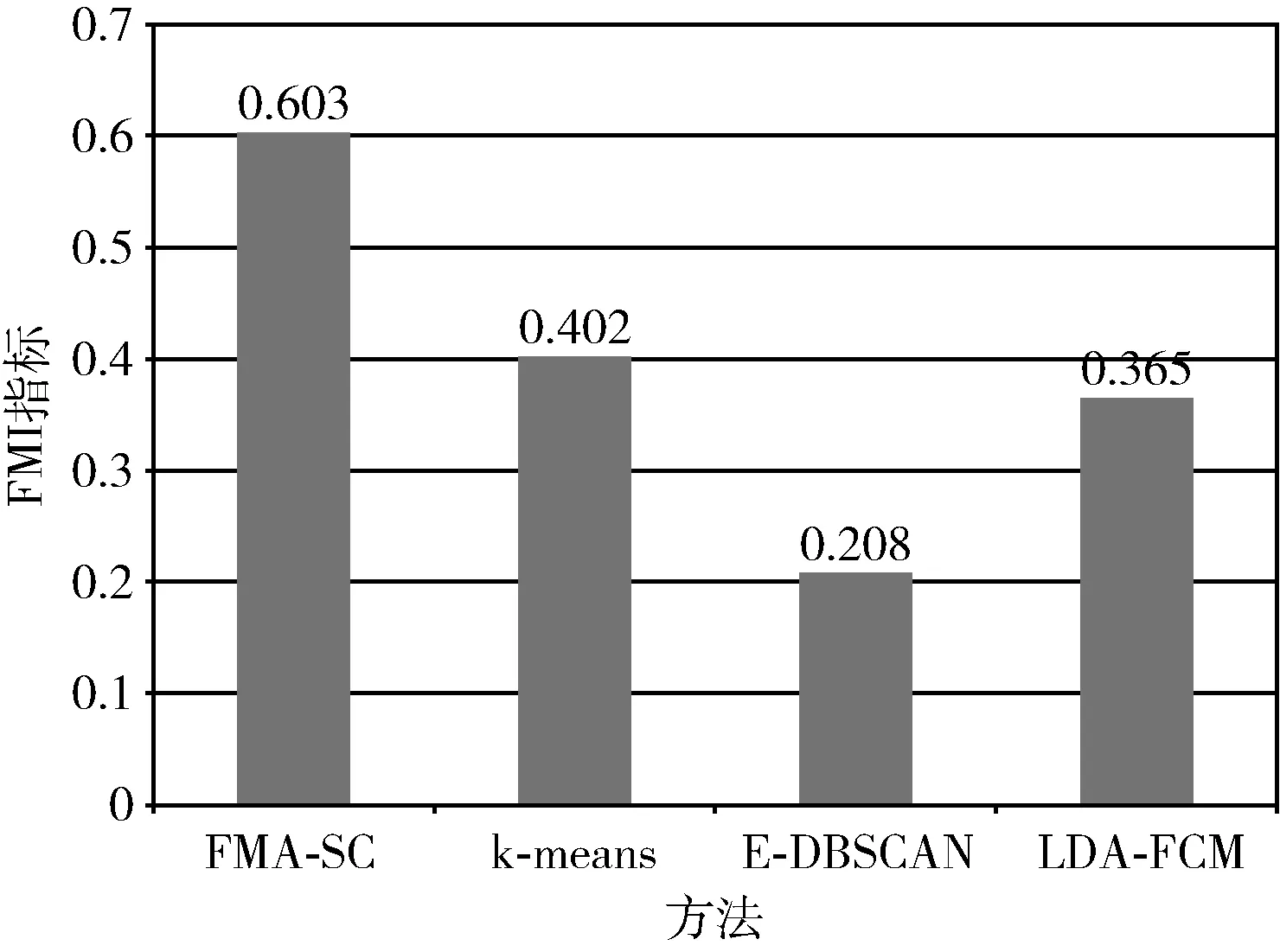
图8 非谱聚类类型算法的FMI指标对比

K-means算法计算云服务之间的综合相似度，构造服务相似矩阵的时间复杂度为O(n2)，n为数据个数，对数据进行处理的时间复杂度为O(nm)，m表示云服务属性个数，获取最佳聚类个数的时间复杂度为O(q2)，q代表类簇个数，该算法综合时间复杂度为O(n2)。 E-DBSCAN算法对数据集的每个对象进行考察，通过检查检查每个点的邻域进行聚类，该算法时间复杂度为O(n×logn)。 LDA-FCM算法提取数据特征、初始化隶属度函数、确定聚类中心时间复杂度为O(n2)， 优化隶属度函数的时间复杂度为O(tn)，t为迭代次数，该算法综合时间复杂度为O(n2)。 本文算法与上述算法相比，时间复杂度处于同一个级别。

从聚类内外部评价指标评分可以得到：本文方法所构建的云制造服务聚类的质量显著优于其它聚类方法，因此，本文所提出的融合多维相似度的云制造服务聚类方法可以有效提升云制造服务聚类的质量。

4 结束语

本文提出一种融合多维属性相似度的云制造服务谱聚类算法。分别构建了云制造服务的文本型和数值型属性相似度矩阵，设计了一种相似度矩阵融合函数，将上述两种矩阵融合，通过融合多维度信息提升了云制造服务的相似度计算精度。引入本征间隙法确定聚类个数，采用的谱聚类算法可以高质量地实现具有非线性样本特征的云制造服务聚类。实验验证，本文方法的聚类质量明显优于当前流行的谱聚类改进算法和其它类型的服务聚类算法。

未来工作主要是结合服务描述文本的语境权重进一步提高文本型属性相似度的计算精度，并在服务聚类的基础上研究相关推荐方法，以进一步提高服务发现的准确度和效率。