基于哈希挑战和随机翻转的WSN通信安全

康 明，席子淳，周 兰，陈 文+

(1.四川大学 网络空间安全学院，四川 成都 610207；2.山东工程职业技术大学 人工智能学院，山东 济南 250200)

0 引 言

无线传感器网络(wireless sensor network，WSN)中，传感器通常通过开放的无线信道向合法融合中心(ally fusion center，AFC)报告本地测量数据，与传统的有线连接相比，无线传感器网络的通信更容易受到数据窃听和其它类型的网络攻击[1，2]。在资源受限的情况下，WSN无法长期承担复杂的加密成本，且因缺乏CA/PKI中心，密钥的可靠交换也是一个挑战[3]。因此，我们需要高效的轻量级的无线传感器网络安全机制。

7、拆卸旧阀门时，最下部一条螺栓不能拆掉，在旧阀门不离开法兰的情况下安装新阀门，待新阀门能够固定在法兰上时，再将旧阀门拆除，防止抽真空过程中突然漏油，新旧阀门都不在法兰上，造成大量绝缘油泄漏。

(1)根据单孔三次定流量抽水试验数据，运用裘布依公式计算渗透系数，新化县孟公集镇泥盆系棋子桥组(D2q)灰岩含水层渗透系数为0.22 m/d。

近年来，一些研究人员[4-11]根据物理层在不同链路上的随机特性和信道的独立性，利用信息论的方法来实现安全通信。在文献[12]中通过聚类方法实现基于信道质量的比特翻转，该聚类方法将传感器节点分组为协作集群以降低能量消耗，减少传感器数据的传输时间。在文献[13]中，研究者对翻转门限进行了优化，并根据传感器的局部检测置信度水平进行传感器之间的交互以节省传输能量。在我们前期的工作[14]中，将安全传输方案扩展到具有多个量化尺度的场景，并使用差分进化算法来优化检测门限。在文献[15]中，将随机数据翻转方案与信息隐藏相结合，以确保高度的数据机密性，只要加密数据的一个比特没有被正确恢复，EFC就不能从捕获的数据中提取真实的测量值。这些新提出的安全方案保证了WSN具有良好的数据保密性。

当前，WSN数据安全性研究很少有安全方案同时考虑了数据的机密性和数据的可信性，以防止窃听和中间人攻击。本文提出了一种轻量级WSN安全数据传输方案加以解决。

1 安全模型

1.1 系统架构

如图1所示，在我们的模型中，n个传感器节点部署在目标区域中，以分布式的方式监视目标的物理状态，在每个传感器si和AFC的两侧预先部署伪随机函数rand(t)。同时，位于AFC附近的敌对融合中心EFC(enemy fusion center)试图捕捉传感器向AFC端发送的传感数据，或对AFC端发起中间人攻击，包括伪造或重传si端发向AFC的数据。

(3)施用“苗壮素”生物复菌剂在一定程度上提高了土壤中速效氮、速效磷、速效钾及有机质的含量。另外，对黄瓜品质和产量也有一定影响，VC、可溶性糖、可溶性固形物含量分别提高16.4%、16%和5%，亚硝酸盐含量显著下降。

智和智拓营销咨询公司总经理颜东从宏观、原材料等多方面对肥料行业近期及未来发展进行了分析。据他介绍，尿素后势企稳，或有阶段性上涨；磷铵涨势已起；钾肥需结合国际大合同结果，呈上涨趋势。他表示，整体而言，化肥行业持续推进供给侧改革，安全、环保持续高压，能源和原料市场高位运行，复合肥的成本压力因此在不断扩大，拥有原料和品质优势的生产企业将会形成明显的竞争优势。

在每一传输周期开始时，AFC首先向传感器发送导频信号 {v，τ1，τ2，τ3，m1，m2，r1} 以开启传感数据的传输，其中v用于测量合法链路上的信道状态信息CSI，如信道增益等，m1，m2是两个随机字符串，r1是一个实数值，τ1，τ2，τ3为翻转阈值，m1，r1，m2共同构成哈希挑战 “hash(m1，r1)=hash(m2，？)”。

在接收到导频信号之后，传感器si将局部测量值mi转换成二进制字符串ai=[ai1，ai2，…aij…ain]，aij∈{0，1}。 随后，si使用当前的信道增益作为rand(t) 的初始种子生成随机序列φi(t)， 根据φi(t)的值控制每个二进制位aij的翻转。传感器和AFC共享变色龙哈希函数的秘密陷门xi。传感器计算应答r2， 使得 和 满足哈希挑战要求。最后，传感器si将 发送到AFC，其中zi是ai的翻转值，sigi是zi的对应签名。

AFC可以利用相同的伪随机函数rand(t) 和初始种子产生随机数序列以恢复ai中翻转过的比特，并检查签名sigi和哈希应答r2以检测可能由EFC发起的中间人攻击。如果签名和应答响应都是合法的，则AFC从合法的zi中提取原始的测量值ai， 从而获得目标的真实状态。而EFC由于其窃密信道与AFC到si的主信道之间的信道独立性，无法侦查得知主信道上的CSI信息。因此即使EFC获取了伪随机函数rand(t)， 也无法生成与si端相同的随机数序列，从而难以恢复出被si翻转了的二进制位。此外，基于翻转的签名和哈希挑战应答能够有效防御EFC端在无线网络发起的中间人攻击，从而本文所提出的安全模型在无线传感网络中同时实现了对传感数据机密性和可靠性的保护。

我国体育教师教育培训主要由职前教育系统和在职培训系统两大系统组成。体育专业院校和师范院校的体育院系主要承担体育教师的职前教育，各级各类的教育学院和教师进修学校主要承担体育教师的在职培训。目前，我国高校中体育教师的培养还存在着诸多问题，其中“训练”比“教育”重要的思想使得体育教师职前教育的课程体系缺乏“师范性”。而体育教师正要通过体育教育学类的课程来学习、掌握和运用来实现其专业的垄断性和不可替代性。因此，建立和完善体育教育学科的课程体系是提高体育教师教育质量、保障体育教师专业地位的重要条件。

1.2 基于翻转加密的数据机密性保护

伪随机函数被预先部署在传感器和AFC的两侧，由于φi(t) 是伪随机函数生成的随机序列，只要在两侧使用相同的初始种子seed，AFC和每个传感器si可以同步产生相同的随机序列。因此，seed由主信道(AFC到传感器)状态信息CSI决定，如信道增益。EFC只能测量其自身到传感器的窃听信道状态，由于信道物理层的独立性，EFC无法测量主信道的状态。

为了旅游电商的快速发展，需加快复合型人才培养速度。 转变传统的人才培养模式，明确培养目标，根据社会实际人才需要，合理安排课程教学，建立旅游电子商务实验室、旅游电子商务实践基地等。将理论知识与校外实践结合起来，培养出更多的旅游电子商务发展的复合型人才，为旅游电子商务的发展提供良好的人才基础。

本文分为如下四个部分：首先对五年规划领域相关的研究与文献进行归纳整理，其次介绍数据库收集及计算方法，再次对实证结果描述与分析，最后对研究结果与发现进行讨论与展望。

如式(1)所示，传感器在每个传输周期t产生一个随机序列φi(t)， AFC使用伪随机函数rand() 和seedi同步产生φi(t)

(1)

在数据传输之前，传感器si本地测量值mi被转换成其二进制格式ai=[ai1，ai2，…aij…ain]，aij∈{0，1}。 并使用式(2)进行概率翻转，即如果φi(t)∈[τ3，τ2]， 则相应位被翻转

(2)

假设φi(t) 遵循均匀分布，λ=(τ2-τ3)/(τ1-τ3) 表示aij的翻转概率，由于WSN的广播性质，EFC可以窃听AFC接收的数据，但它不能区分翻转的位和原始的未翻转位，也无法从窃听的数据中提取有用的信息。而AFC可以使用相同的随机序列轻松恢复翻转的比特：如果接收到的二进制为zi=[zi1，zi2，…zij…zin]， 那么它将以1⊕zij，ifτ3<φi(t)<τ2进行翻转zij， 以恢复原始测量数据。

1.3 基于变色龙哈希挑战的数据可靠性保护

传统上，WSN数据安全研究关注的主要是无线传感器网络中的数据机密性，但我们不能忽视EFC在无法获取原始测量值的情况下，可以通过数据拦截向AFC端发动中间人攻击。例如，它可以向AFC重放捕获的(或伪造的)数据。为了保护WSN传输免受中间人攻击，本文在安全机制中加入了变色龙哈希挑战。

如1.1节所述，在每个传输周期的开始，AFC首先向传感器发送导频信号 {v，τ1，τ2，τ3，m1，m2，r1}， 其中m1，m2是两个随机串，r1是一个实数值，它们构成变色龙挑战 “hash(m1，r1)=hash(m2，？)”。 传感器需要对挑战做出响应：如果它已经找到r2， 并满足hash(m1，r1)=hash(m2，r2)。 变色龙散列的设计如式(3)和式(4)所示

hash(m1，r1)=gm1yr1modp

(3)

hash(m2，r2)=gm2yr2modp

(4)

gm1yr1modp=gm2yr2modp

(5)

从式(5)中我们可以看出，如果gm1+xr1=gm2+xr2， 则可以很容易地利用式(6)中的陷门x轻松计算r2

(6)

为防止EFC窃听，传感器和AFC不会通过开放的无线信道协商陷门x。在本文中，陷门x在主信道的两侧使用式(1)的伪随机函数的输出来进行同步，使得x=gφi(t)modp。 因此，EFC不能通过数据窃听获得陷门，也就难以完成哈希应答挑战。

1.4 基于翻转签名的数据完整性保护

同时为了防止攻击者非法篡改截获的传感数据zi为z′i， 然后转发z′i到AFC以破坏数据的完整性，模型中引入数据签名机制对传感数据的完整性进行保护。由于传统的RSA、DSA、ECDSA等签名算法时间代价较高，较难直接应用于WSN的资源受限环境。本文利用传感器端与AFC端同步产生的伪随机数据序列，设计了翻转签名方法。

最后，传感器si将传感数据zi， 签名sigi， 哈希挑战的应答r2组合成最终的结果 ， 并发送给AFC。

如式(7)所示，传感器si基于伪随机函数产生的随机数序列，对待发送的数据zi=[zi1，zi2，…zij…zin] 生成对应的翻转签名

对于电气自动化控制设备，在设计时我们要充分的研究和分析电气自动化控制设备各部件的技术要求、数据参数等信息，确保其设计科学合理性；对于市场上多种多样的元器件，要对其质量的稳定性以及可靠性进行对比，选择质量优、价格合理的零件。

(7)

其中，sigij是sigi的第j位。

爸爸一直在门口等着，妈妈早已经把饭做好，说了好几次让爸爸先吃着，可爸爸就是不肯，说孩子没回来这饭咋吃啊!

1.5 效率分析

由于数据加密和签名保护过程都只需要进行最基本的比特翻转操作，避免了传统加密算法中迭代进行的复杂的移位、异或、模加等运算，因此，本文提出的数据机密性和完整性保护方法计算效率更高，适用于资源受限的WSN网络环境。

如图2～图3所示，我们给出了本文数据翻转加密和签名过程与传统的加密算法和签名过程的效率对比。

图2 加密过程时间代价

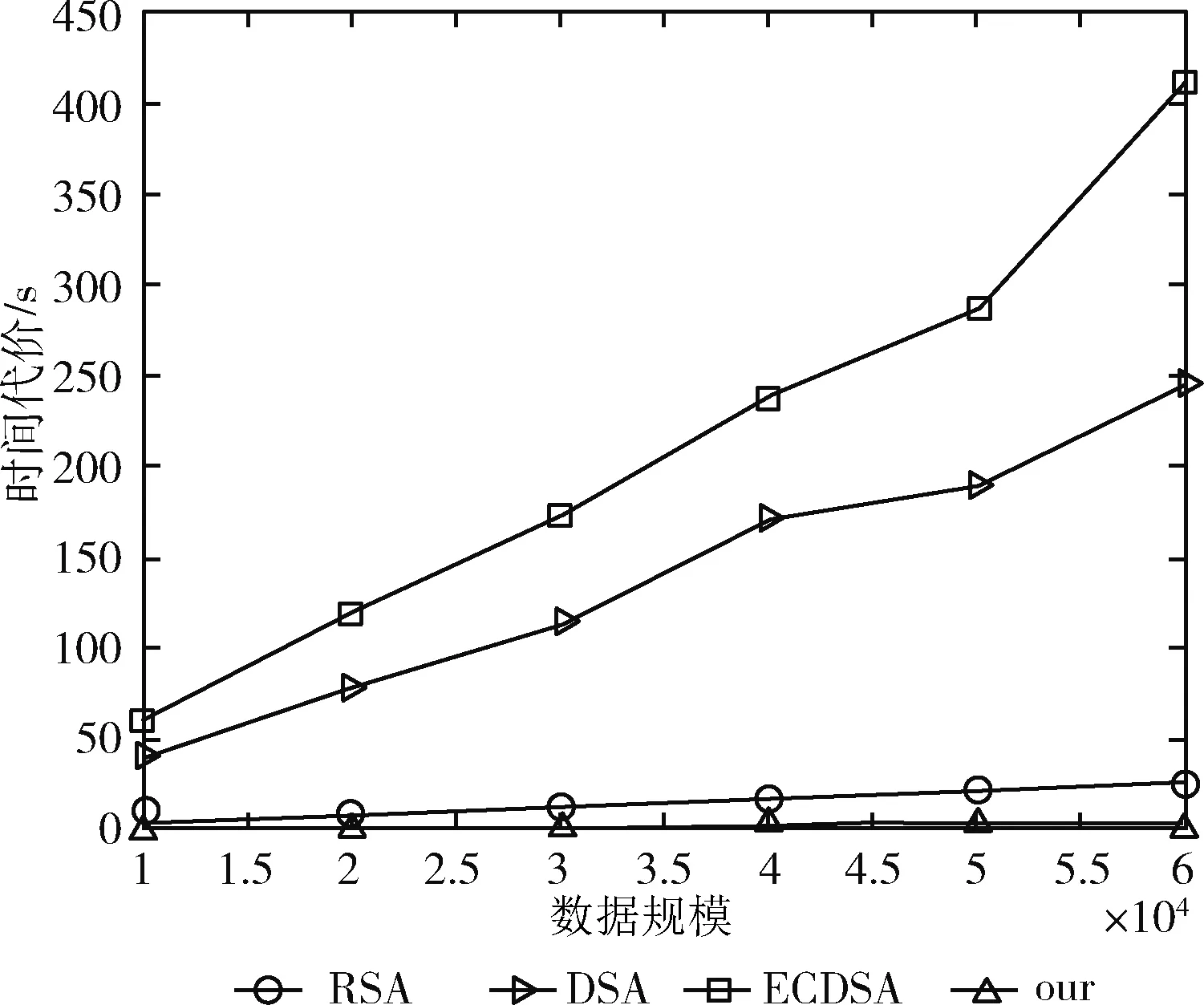
图3 签名过程时间代价

同样，我们通过式(12)计算f(ziE|θ0)

随着卫生改革的深入发展,从单纯的生理服务转向生理、心理、社会的全面服务,从单纯的技术服务转向社会性服务。体现健康促进与健康教育重要性和必要性。成立健教专家库,发挥志愿者的作用,进学校、工地、社区、老年公寓、福利院、农村举办健康教育大课堂、义诊宣传、免费送医送药送健康等活动,使百姓足不出户,就能享受到医疗专家的服务,并举办全国庆三八大型公益活动,关爱女性健康从防治两癌开始健康教育大课堂及义诊、咨询活动,每年为100名低收入女性免费宫颈癌筛查;连续三年荣获了中国癌症基金会健康教育“公益活动三等奖”和“社会公益奖”奖杯。

2 安全性分析

在这一节中，我们分析了所提出的方案的安全性，主要关注的是EFC可以从传感器和AFC之间的通信中窃听获得多少有效信息，以及EFC能否成功发动中间人攻击。

2.1 数据保密的安全性

假设被窃听的传感器数据是zE=z1E…ziE…znE， EFC必须判断ziE是否已经翻转。如式(8)所示，θ1代表ziE没有翻转，而θ2恰恰相反。如果L大于阈值，则结果为θ1， 否则为θ2

(8)

从式(8)可知，数据机密性可以通过推导f(ziE|θ1) 等于f(ziE|θ0) 来实现，这使得在EFC的LLR结果总是等于零。当L=0时，EFC不能区分翻转的比特和原始的比特，必须忽略窃听到的数据。通过用式(9)来分析f(ziE|θ1)

(9)

其中，m1、r1和r2是椭圆曲线上的点。使用陷门x，传感器和AFC可以很容易地计算r2。 但是，在不掌握陷门x的条件下，EFC不可能在多项式时间内找到合法的r2。

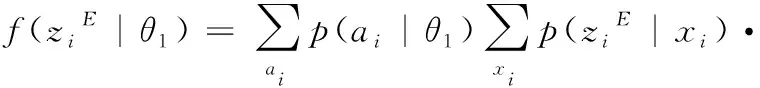
(10)

传统课堂上往往先由教师讲解中药的性状特征，然后让学生观察中药实物标本进行印证，没有充分发挥标本的作用。笔者设计了“链条式应用标本”课例，让学生真正围绕标本自主参与到教学中来。课例各环节设计如下。

f(ziE|θ1)=f(ziE|xi=1)·p(1|θ1)·λ1+
f(ziE|xi=1)·p(0|θ1)·λ2+f(ziE|xi=0)·
p(1|θ1)·λ1+f(ziE|xi=0)·p(0|θ1)·λ2

(11)

在图2～图3中，Simon、Speck是轻量级分组加密算法，其加密效率较高，被应用于WSN数据安全性保护过程。RSA、DSA、ECDSA是当前广泛采用的数据签名算法。随机生成1万～6万规模的8*100位二进制位串，代表受保护的传感器数据。从图2～图3中可以看出，在相同的数据规模下，本文所提出的方法时间代价远低于传统的算法。这是由于本文提出的方法利用了伪随机函数同步控制下的比特位高效翻转过程实现了加密与签名过程，相较于传统的移位循环移位、异或加密处理流程，数据位翻转的计算复杂度和时间代价更低。此外，本文提出的方法通过伪随机数序列自动实现了加密数据恢复，减少了对密钥安全分发过程的依赖，因此更适用于WSN的开放式且资源受限环境下的数据安全保护过程。

f(ziE|θ0)=f(ziE|xi=1)·p(1|θ0)·λ1+
f(ziE|xi=1)·p(0|θ0)·λ2+f(ziE|xi=0)·
p(1|θ0)·λ1+f(ziE|xi=0)·p(0|θ0)·λ2

(12)

通常，出现在二进制字符串中的比特“1”或比特“0”的概率是相同的，可以假设p(1|θ1)=p(0|θ1)=p(0|θ0)=p(1|θ0)=0.5， 这意味着式(11)与式(12)相同。因此，等式(8)中L是0，EFC由于不能区分翻转的比特和未翻转的比特，只能完全忽略捕获到的数据。

2.2 抗中间人攻击分析

如1.3节所述，为了防御重放攻击，在每个传输周期开始时，AFC向传感器发起新的挑战：为m1、m2和r1找到r2以满足hash(m1，r1)=hash(m2，r2)。 AFC接收到传感数据后，首先检查其中的哈希应答响应r2是否满足本轮传输周期开始时发送给传感器端的哈希挑战。

传感器和AFC具有相同的陷门x=gφi(t)modp， 其中φi(t) 由式(1)同步计算。EFC无法感知x，也就无法计算出合法的r2， 因此，它只能通过式(13)穷举搜索x

gm2yr2modp=gm1yr1modp

(13)

其中，φi表示式(1)中伪随机函数的值，f(φi) 表示其概率密度函数，ai和xi分别表示第i个传感器si的原始比特和最终输出比特。当xi已知时，ziE条件独立于ai、φi和θ1， 当φi和ai已知时，xi条件独立于θ1。 根据式(2)，如果φi∈[τ2，τ1]， 则该位不翻转，否则该位翻转。因此，我们可以得到式(10)

在每个传输周期开始时，AFC首先向传感器发送导频信号 {v，τ1，τ2，τ3，m1，m2，r1}， 以发起新一轮的数据传输，其中 {τ1>τ2>τ3} 是翻转阈值，v为评估信道状态的参数，m1，m2和r1代表用于防御重放攻击的变色龙哈希挑战的参数。传感器向AFC报告 {v，ack}， 以确认收到导频信号。

一旦AFC从传感器si接收到响应 ， 它将验证r2是否等于 (m1-m2)/x。 如果r2≠(m1-m2)/x， AFC放弃zi， 否则它使用式(14)生成签名sig′i， 并进一步检查签名sig′i是否与sigi相同

(14)

只有当r2满足哈希挑战应答，且sig′i=sigi时，AFC端才接受zi为合法的传感数据，否则将丢弃zi， 并开启新的发送周期，要求传感器si重传数据。

如前所述，只有传感器和AFC知道φi(t) 及其初始种子，从而确保了EFC不能将zi修改为z′i并将其与新的合法签名sig′i一起发送给AFC。如果EFC只是在同一个传输周期内将捕获的数据重放给AFC，对AFC的数据融合没有影响；如果EFC重放的数据跨越不同的周期，AFC可以发现得到的哈希响应r2与 (m1，r1) 不匹配，重放的攻击数据将被丢弃。

3 实 验

在这一部分中，我们将本文的方案与Zhou等[15]、Jeon等[16]和Chen等[17]提出的安全机制进行了比较，以测试其抵御窃听和中间人攻击的性能。在文献[15]中，传感器的测量值根据预先部署的Rand随机翻转，且翻转的数据通过信息隐藏技术进行编码以增强保密性。在文献[16]中，传感器的测量数据基于主信道的瞬时信道增益动态地进行翻转。文献[17]中提出了优化的融合规则Optimum-LLR，在对比实验中用于衡量融合中心的错误概率下界，然而Optimum-LLR没有采取任何安全策略来防止来自EFC的攻击。

为了便于比较，我们采用了类似文献[16]中的实验环境设置，其中传感器被部署成星形拓扑，主信道增益被假设为遵循瑞利分布，传感器的本地检测性能相同：传感器的本地错误检测率Pf_local=0.2， 本地真实检测率Pd_local=0.9。 在设计任何安全方案或技术后，必须执行的最重要步骤之一是使用合适的指标正确评估和量化其保密性能，性能评估必须反映所提议的方案或方法可以提供多少保密性。本文以加权误差概率Pweight=Δ(1-Pd)+(1-Δ)Pf作为融合性能的衡量标准，其中Pd和Pf分别为融合中心的检测概率和虚警概率，Δ=0.5为加权因子，我们在式(11)、式(12)中设置翻转参数λ1=λ2=λ。 通过描述AFC和EFC之间加权误差概率的差异作为安全吞吐量，与保密信道容量相关联，从而执行基于SINR(signal to interference plus noise ratio)的保密性能指标[18]。

在第一轮模拟中，我们只考虑了EFC试图从公开信道窃听传感器数据的情况。在窃听期间，EFC不向AFC重放或注入伪造的数据。图4～图7中描绘了不同信噪比SNR和传感器数量下AFC和EFC的加权误差概率。

从图4和图6中我们可以看到Optimum-LLR达到了最低的错误概率(下限)。然而，Optimum-LLR没有采取任何安全机制来防止窃听，因此EFC也可以获得与AFC相同的低错误率。对比结果表明，本文的方法和Zhou在AFC端的错误概率接近Optimum-LLR的错误概率，并且明显优于Jeon的方法。这是因为AFC采用与传感器发送端相同的伪随机序列，可以使用反向翻转完全恢复原始测量数据。另一方面，从图5和图7中我们可以看到，即使在高信噪比和大量传感器的情况下，EFC的错误概率也总是接近50%，因为它无法区分翻转的比特和原始比特，这使得敌方的数据融合完全受到干扰。上述方法除Optimum-LLR，均实现了信息论上的理想保密，防止了EFC得到正确的融合结果。

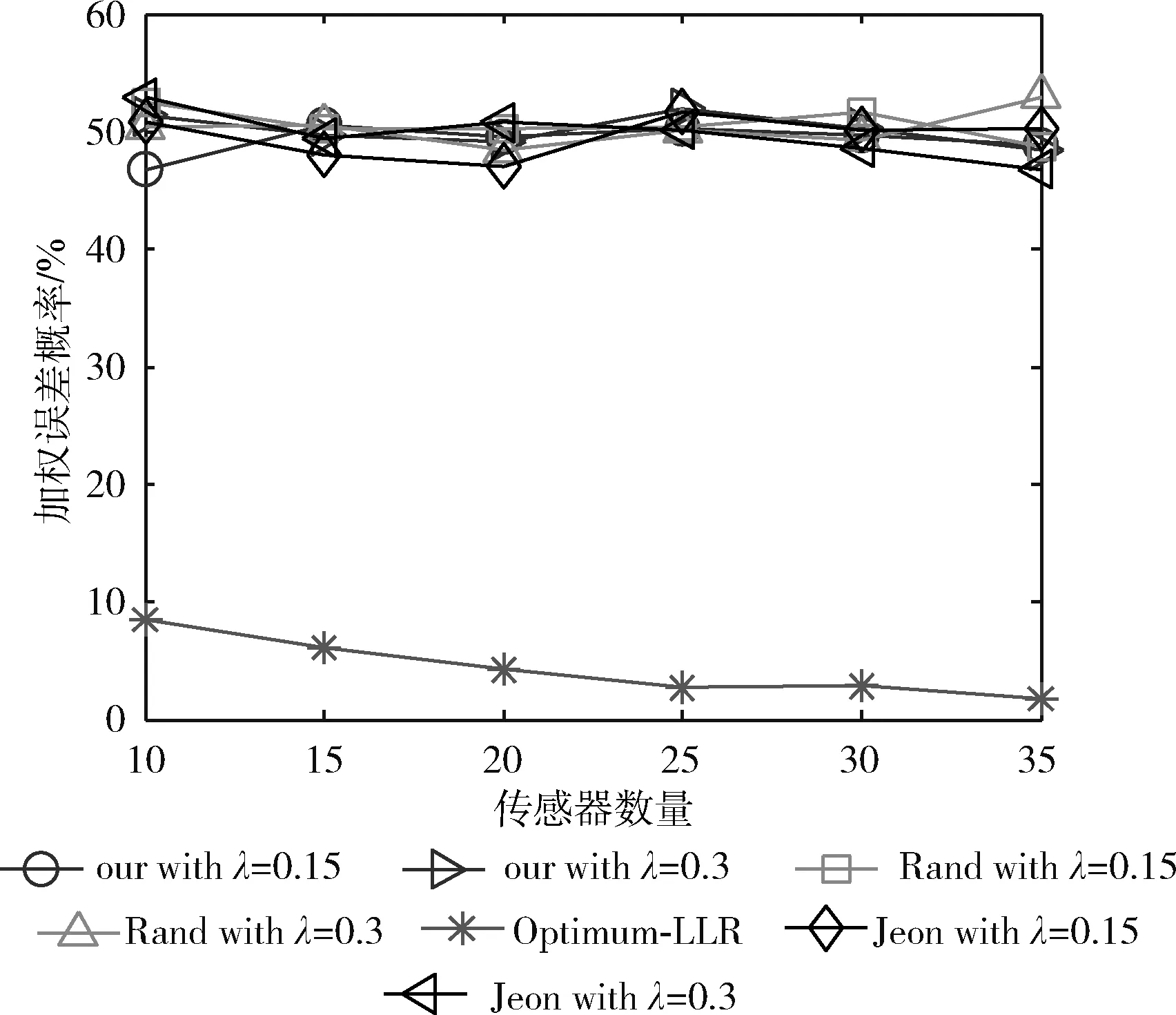
图5 理想环境下EFC在不同数量的传感器下的Pweight

图6 理想环境下AFC在不同信噪比下的Pweight

图7 理想环境下EFC在不同信噪比下的Pweight

然后，我们设计了另一组模拟更真实的网络环境的对比实验：在20%的传感器数据被重放或伪造的数据随机干扰的情况下进行窃听和中间人攻击，实验结果如图8～图11所示。

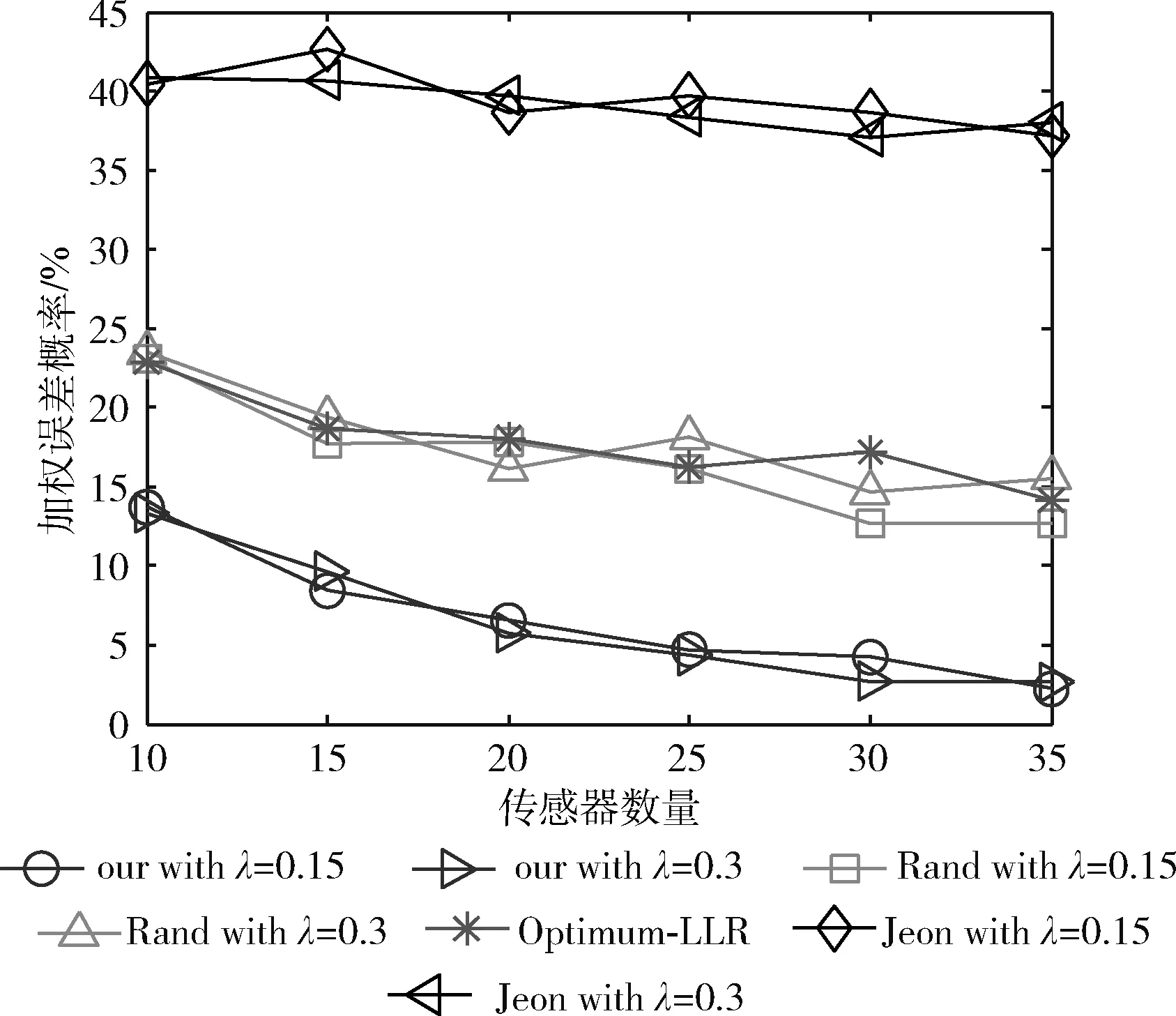
图8 非理想环境下AFC在不同数量的传感器下的Pweight

图9 非理想环境下EFC在不同数量的传感器下的Pweight

图8～图11的结果表明，对于我们的方法，在AFC端，Pweight随着SNR和传感器数量的增加而降低，而在EFC处，Pweight始终接近50%。值得注意的是，与第一轮比较的结果相比，由于Zhou和Jeon将所有接收信号作为数据融合的合法输入，EFC端的重放或伪造数据干扰了AFC的数据融合，降低了其数据融合精度，AFC的错误概率明显增加。本文方法的AFC错误概率与其相比降低了10%到25%。从图8和图10可以看出，本文方法的AFC的错误概率明显低于20%(被攻击数据率)。如1.3节所述，来自传感器的响应包含3项：， 其中sigi是基于预先部署的随机函数的数据zi的签名，r2是对挑战的响应。EFC不知道哈希陷门x，无法通过式(6)计算r2。 此外，传感器响应zi与其签名sigi一起发送，由于EFC在缺失φi(t) 的情况下难以伪造合法的签名sig′i， 从而确保了EFC不能伪造对AFC的回复 。 因此，通过验证数据签名和挑战应答机制，AFC可以容易地检测到中间人攻击。虽然AFC丢失了20%的传感器数据，这些数据被EFC使用重放(或伪造)数据用来模拟中间人攻击所取代，但丢失的数据可以通过来自其它未修改数据的合法响应来补偿。结果表明，本文的方法能够有效地保护AFC免受窃听攻击和中间人攻击。

对UPS的运行状态进行实时监测管理，但不对UPS进行控制。通过UPS自带的智能通讯接口和相应的通讯协议内容，实时显示并保存UPS的运行参数、运行状态，储能电池soc参数及报警信息进行实时监测；能用直观的图形来指示UPS的运行状态。实时判断UPS的部件是否发生报警，当UPS的某部件发生故障或越限时，监控主系统发出报警。

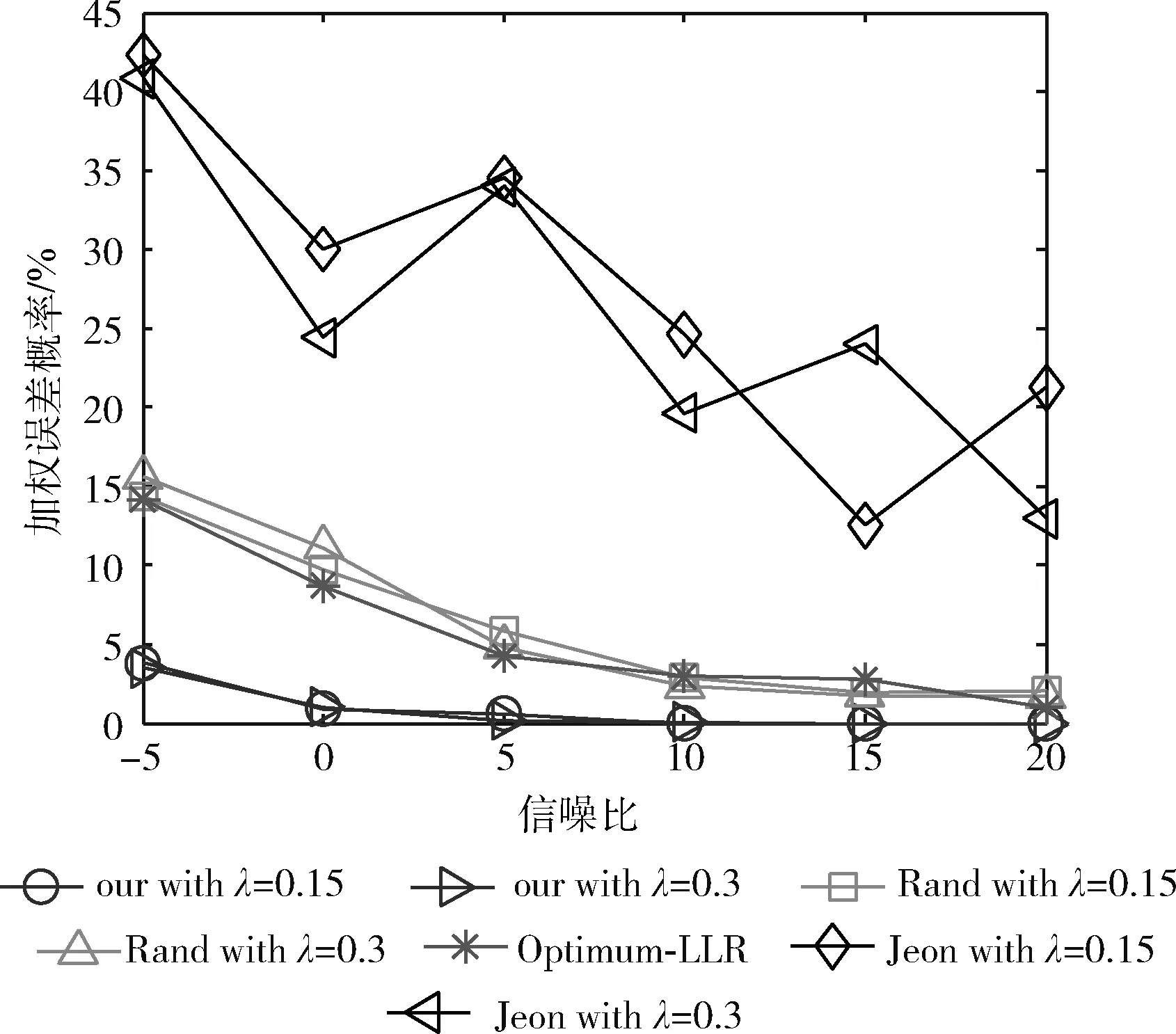
图10 非理想环境下AFC在不同信噪比下的Pweight

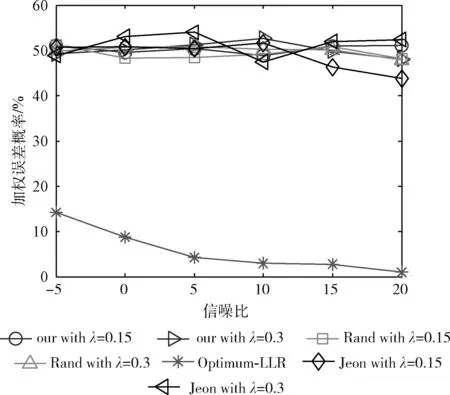
图11 非理想环境下EFC在不同信噪比下的Pweight

4 结束语

本文针对无线传感器网络中的数据安全传输问题，提出了一种基于哈希挑战和随机翻转的WSN通信安全方案，并完成了与传统方案在效率、数据的机密性和防范中间人攻击上的对比验证。实验结果表明，本方案实现了信息论上的理想保密，且计算效率更高，当20%的传感器数据被攻击者利用中间人攻击进行干扰时，本文方法的AFC的数据融合错误概率能够保持在5%到10%，AFC的错误概率明显低于20%(被攻击数据率)，而窃听者的错误概率始终接近50%。

本文所提出的方案同时考虑了数据的机密性和数据的可信性，并且传感器付出代价较低，适用于WSN资源有限的情况。在未来的工作中，我们将继续提高WSN通信抗中间人攻击的能力。