冻融条件下岩石动态损伤本构模型

张慧梅,赵 洁,陈世官,申艳军,路亚妮,刘 慧

(1.西安科技大学理学院,西安 710054;2. 西安科技大学 建筑与土木工程学院,西安 710054;3. 湖北工程学院土木工程学院,湖北 孝感 432000)

随着国家“一带一路”战略的实施及基础设施建设的发展,寒区蕴藏的矿产、森林、土地及旅游等资源越来越受到重视,大量的基础建设正在或将在寒区建设。但受赋存环境的影响,寒区岩石由于长期受冻融循环影响,内部缺陷不断萌发、扩展,损伤持续累积,导致岩石力学性能劣化。此外,岩石承受的荷载类型越来越复杂,不但包括自重、上部建筑物等静态荷载,还包括冲击、爆破、地震及滑坡等动态荷载[1],例如矿山开采、大型机械掘进、岩爆等动力工程以及地震、滑坡等自然灾害的防治中,越来越多地涉及动荷载作用。在动荷载条件下,岩石由于承受快速变化的外荷载,表现出明显的动态力学特性,与静态力学特性存在显著区别,破坏模式也随之变化。所以,寒区岩石受冻融与动荷载2种损伤因子的共同作用,其变形破坏正是2种损伤耦合扩展效应的累积,必须从损伤的本质特性出发,对冻融条件下岩石的动态损伤破坏问题进行研究。

近年来,关于动荷载条件下冻融岩石的损伤破坏及力学特性方面,国内外众多学者取得以下研究成果。Bo Ke等[2]研究不同冻融条件及轴向应力下砂岩的动态力学特性;Luo Y等[3]对不同冻融次数下砂岩静动态力学参数的变化规律及破坏模式进行研究;Ma Q Y等[4]基于不同冻融次数下软岩的SHPB试验,研究冻融循环对能量比吸收率、反射率及透射率等能量分布参数的影响;Li J L等[5-6]研究冻融循环对岩石孔隙结构和动态力学特性的影响;Wang P等[7-10]开展不同冻融次数下岩石的动力学特性试验,研究冻融岩石的动态力学特性及损伤破坏过程;刘少赫等[11]开展SHPB试验研究冻融红砂岩的动力学特性,并通过扫描电镜分析冻融作用下红砂岩的细观损伤;闻磊等[12]通过室内试验数据与数值模拟结果,对动荷载条件下冻融岩石的强度特性进行研究;宾峰[13]对冻融条件下岩石的静、动态力学特性进行对比,研究冻融循环与轴压共同作用下岩石的动态力学特性,分析岩石的动态损伤演化过程;柳森昊[14]研究砂岩在静态与动态两种荷载下力学参数的变化规律,并通过扫描电镜试验分析冻融砂岩的损伤破坏特征。

以上研究皆从试验层面对冻融岩石的动态力学特性进行研讨,较少通过建立理论模型,研究其变形破坏的力学行为,揭示冻融损伤与动荷载损伤的耦合效应,反映损伤的本质特性。因此,在充分考虑冻融损伤的影响的基础上,运用Mises破坏准则,构建冻融条件下岩石的动态损伤本构模型,确定模型参数的理论表达式;描述其变形破坏过程,刻画冻融与动荷载损伤的耦合效应,反映冻融次数及应变率对岩石总损伤、模型参数和变形破坏特性的影响。

1 岩石动态变形破坏过程

文献[3,11]通过岩石SHPB冲击压缩试验对岩石动态力学行为进行充分研究,认为岩石的变形破坏经历5个阶段(见图1)。

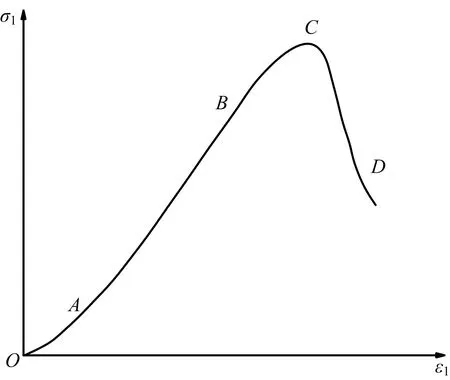
图 1 岩石动态变形破坏过程Fig.1 The dynamic deformation and failure process of rock

1)压密阶段(OA段)。动荷载作用下,岩石内部原有的微孔隙、微裂隙发生压密闭合,曲线呈上凹形;但高应变率下,荷载持续效应太短,岩石内部缺陷来不及闭合,压密阶段并不明显。

2)弹性变形阶段(AB段)。随应变的增加,σ-ε曲线近似线性发展,动弹性模量基本不变,卸荷后应变形态可以恢复;整个变形破坏过程中,此阶段岩石抵抗冲击变形的能力最强。

3)塑性变形阶段(BC段)。此阶段曲线斜率减小,至峰值点(C点)时斜率为0,呈上凸形;此时岩石处于非线性变形阶段,损伤持续累积,抵抗变形能力减弱。

4)应变软化阶段(CD段)。该阶段曲线应变缓慢增加,应力迅速下降,未出现回弹现象,说明岩石内部缺陷扩展、贯通,并形成贯通区,产生断裂面,造成不可逆的损伤、破坏。

5)损伤破坏阶段(D点以后)。此阶段岩石变形继续增加,内部断裂面之间的黏聚力丧失,承载能力不足,岩石发生宏观破坏。

此外,冲击荷载作用下,由加载速率不同而产生的应变率效应问题是岩石静力学与动力学的本质区别,随着应变率的增加,岩石内部微结构变形导致的“惯性力”不容忽视[1]。“惯性力”将导致岩体内部颗粒处于相对运动状态,其内摩擦力产生黏滞阻抗效应,表现为黏滞特性。

综上所述,岩石动态变形破坏过程表现出了明显的弹塑性特征、应变软化特性及黏滞性。

2 冻融岩石动态损伤本构模型

2.1 力学模型

一般来说,本构模型应具有简单的数学表达式、较少且易于确定的模型参数,且能够反映材料的主要特性。所以,必须选择合适的数学描述方法对岩石的损伤进行合理表征,尽可能满足本构模型的理论严谨性和工程实用性。

根据岩石动态变形破坏过程分析,岩石在动荷载作用下能够表现出较为明显的弹性、塑性及应变软化等力学特性。事实上,岩石材料在受力状态下的破坏是从随机分布的细观缺陷到宏观破坏的非线性演化过程,是损伤的持续累积。所以,将以上力学特性概化为损伤特性是一种简洁有效的研究手段。

因此,本模型考虑利用损伤体描述岩石材料所具有的弹塑性变形特征、应变软化特性,利用黏性体表达岩石材料的黏性特征。为了能够同时体现岩石的损伤特性和黏滞性,将岩石内部微元体视为理想化的损伤体与黏性体的并联组合体,如图2所示。

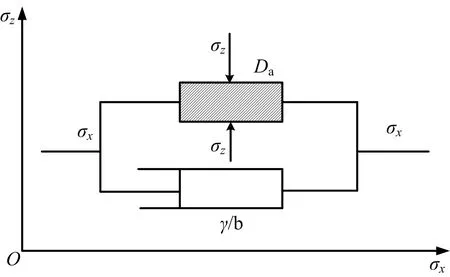
图2 岩石微单元体模型Fig.2 Rock microelement model

假设岩石在x方向承受冲击荷载,由损伤体与黏性体并联关系可知

(1)

式中:εa为损伤体应变;εb为黏性体应变;σa为损伤体应力;σb为黏性体应力。

2.2 损伤本构方程

冻融循环作用下损伤演化的力学效果可以通过材料宏观基准量的劣化来表达。选用弹性模量的劣化度量不同冻融次数下岩石的受损程度,将冻融损伤变量Dn表示为

(2)

式中:E0为未冻融岩石的动弹性模量;En为不同冻融次数下岩石的动弹性模量。

假设岩石由若干具有不同缺陷的微元体组成,从宏观角度出发,根据连续介质力学理论,该微元体的尺寸足够小,能够作为一个质点来考虑;从细观角度来看,该微元体的尺寸足够大,包含足够多的微裂纹、微空洞等细观缺陷[15]。

基于岩石内部结构的非均匀性质及受荷过程中内部微元破坏的随机性,假定岩石微元强度服从Weibull统计分布,其概率密度函数为

(3)

式中:F*为岩体微元强度随机分布的分布变量;m和F0为Weibull分布参数。

岩石的变形破坏是材料内部微元体损伤破坏的累积效应,对式(3)进行积分可将岩石的受荷损伤变量表示为

(4)

以岩石的冻融损伤为第一损伤状态,冻融岩石的受荷损伤为第二损伤状态,根据推广后的应变等价性假设[16],冻融岩石的受荷损伤本构关系可表示为

σx=En(1-Ds)εx+2μσz

(5)

σz=En(1-Ds)εz+μ(σx+σz)

(6)

根据式(2)及式(5)、式(6),可得冻融循环作用下受荷岩石的损伤本构关系为

σx=E0(1-D)εx+2μσz

(7)

σz=E0(1-D)εz+μ(σx+σz)

(8)

其中,

D=Ds+Dn-DsDn

(9)

式(9)为冻融-动荷载耦合下岩石的总损伤变量。可以看出,冻融-动荷载的共同作用加剧了岩石的总损伤,但两者的耦合效应在一定程度上又使得岩石的受损程度有所减弱,并呈非线性关系。分析认为,冻融循环作用导致岩石产生冻融损伤,但岩石内部晶粒在荷载的作用下发生错动、滑移又对孔隙水冻结成冰时所产生的体积膨胀有所限制,表现为冻融与动荷载的耦合作用对总损伤产生的弱化效应。

将式(2)与式(4)代入式(9),可将冻融受荷岩石的总损伤变量表示为

(10)

联立式(7)、式(8)与式(10)可得损伤体的本构关系为

(11)

对于黏性体而言,在外荷载作用下遵循黏滞定律,应力与应变率呈线性关系,其本构关系为

(12)

将式(11)与式(12)联立,代入式(1),可得冻融岩石的动态损伤本构关系为

(13)

(14)

假定岩石的损伤破坏准则服从Mises强度理论,则式(13)～(14)中的分布变量F*可表示为

(15)

式中:J2*为有效应力偏量的第二不变量,其表达式为

(16)

根据损伤的定义,有

(17)

式中:σi为名义应力;σi*为对应的有效应力。

联立式(15)、式(17),可得F*的表达式为

(18)

式中:

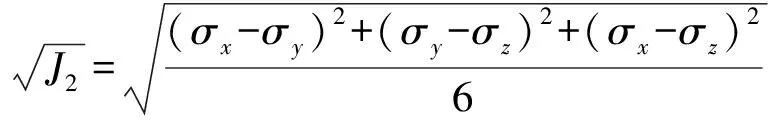
(19)

2.3 模型参数的确定

模型参数m和F0可通过应力-应变曲线峰值点(σc,εc)处满足的几何条件获得其理论表达式。

①εx=εcn时,σx=σcn;

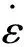
(20)

(21)

对式(13)～(14)两边取全微分有

(22)

(23)

(24)

(25)

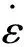
(26)

(27)

将式(24)～(27)代入式(22)～(23)中可得

(28)

(29)

式中

联立式(28)～(29)消去dσz,可得到dσx的表达式,再与式(20)比较,并根据极值条件②,有

(30)

化简式(30)可得

(31)

根据式(13)和极值条件①得

(32)

联立式(31)和式(32)可得模型参数m和F0的理论表达式为

(33)

(34)

3 模型参数讨论

为明确模型参数的物理意义,现引用文献[14]冻融砂岩力学特性试验结果进行分析讨论。

3.1 冻融砂岩动态力学特性试验结果

文献[14]以高径比为1:2的圆柱形砂岩为研究对象,对烘干、饱水处理后的试样进行温度变化周期为+20 ℃～-20 ℃～+20 ℃的冻融循环试验,随后对经历不同冻融循环次数(0、1、5、10、15、20次)的试样进行5组不同应变率下的SHPB冲击试验,探究冻融条件下砂岩的动态力学特性。具体力学参数[14]如表1所示。

表1 不同冻融次数及应变率下岩石的力学参数

3.2 模型参数的物理意义

利用表1试验数据代入式(33)～式(34)进行计算,可绘制冻融次数为20次、应变率为65.1 s-1时模型参数不同取值的σ-ε曲线(见图3),从而可讨论模型参数对曲线形态的影响,揭示其物理意义。

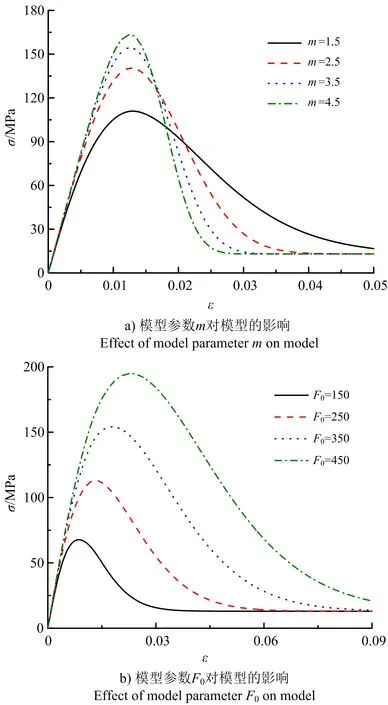
图3 模型参数对模型曲线的影响Fig.3 Effect of model parameters on model curves

由图3a可知,随参数m的递增,曲线峰前塑性屈服段及峰后软化段坡度越来越陡,峰后应力降低速度不断增加,说明岩石延性特征减弱,脆性特征增加。因此,参数m反映了岩石的延脆性特征,表征岩石内部微元强度分布的集中程度。

由图3b可知,随参数F0的递增,曲线峰前阶段的弹性变形部分基本一致,但塑性屈服阶段之后的部分表现为整体右移,依次平行排列,最终近似趋于水平直线。参数F0对σ-ε曲线的改变主要体现为曲线的峰值强度依次增加,反映了岩石微元宏观平均强度的大小。

4 冻融岩石动态损伤力学特性分析

4.1 物理力学特性分析

4.1.1 抗冻性分析

文献[17]利用抗冻系数Rd来表示岩石抵抗冻融破坏能力的强弱,表达式为

(35)

式中:σc为未冻融岩石的动态抗压强度;σcn为不同冻融次数下岩石的动态抗压强度。

根据表1及式(35),可绘制不同冻融次数n及应变率下岩石抗冻系数Rd的变化曲线(见图4)。

图4 抗冻系数变化Fig.4 Change of frost resistance coefficient

从图4可以看出,随冻融次数的增加,岩石的抗冻系数呈减小趋势,且冻融前期降低幅度最大,之后下降趋势变缓。说明岩石的抗冻性能随冻融次数的增加而减弱。当应变率分别为65.02、75.07、84.87 s-1时,对应的抗冻系数分别减小13.49%、10.71%、10.33%。这是由于岩石内部水-冰相变及多种矿物成分的不均匀收缩膨胀作用导致微缺陷萌发、扩展,并随冻融次数的增加而扩大,各项基本力学性能逐渐衰减,抵抗冻融破坏的能力降低,但冻融前期岩石内部结构和连结受到的破坏严重,所以抗冻系数显著降低。

从图4还可以看出,冻融前期,抗冻系数随应变率的增大而降低,但随冻融次数的增加,不同应变率下抗冻系数曲线相继相交,相交后抗冻系数随应变率的增大而增加。这是因为冲击荷载产生的惯性力作用限制了岩石的侧向变形,且限制作用随冻融循环及应变率的增大而增强,由此岩石的应力状态近似于被动围压状态,表现出了应变率强化效应[18],所以抗冻系数有所增加。

4.1.2 动载强度分析

依据表1中的力学参数,绘制动态抗压强度随冻融次数和应变率的变化曲线(见图5)。

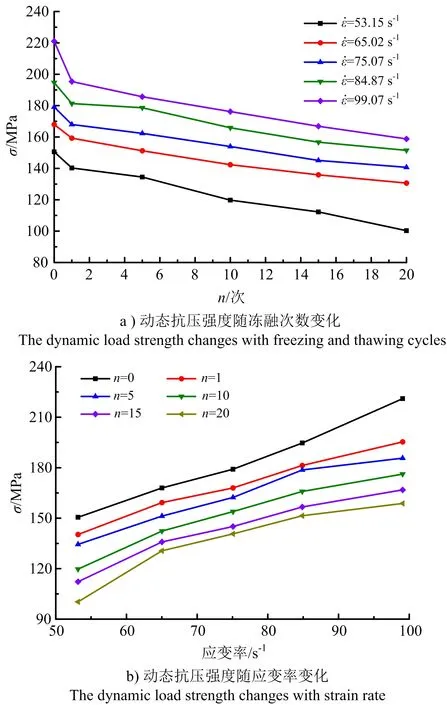
图5 动态抗压强度随冻融次数、应变率变化Fig.5 The dynamic load strength changes with freezing and thawing cycles and strain rate

分析认为,在冻融循环作用下,岩石内部水-冰相变产生的冻胀力克服黏聚力,促进微观缺陷进一步扩展,物理力学性质劣化,所以动态抗压强度减小;但由于水-冰相变导致的微裂隙扩展在冻融初期表现最显著,且可以容纳冻融后期水-冰相变的体积膨胀,所以冻融初期动态抗压强度显著降低,而后期下降幅度减缓。说明此时岩石内部基本达到新的平衡状态,力学性质的变化逐渐稳定。

由图5b可知,岩石动态抗压强度与应变率呈正相关,变化速率先快后慢。当冻融次数为1,应变率为53.15 s-1时,岩石的动态抗压强度为140.28 MPa,应变率为65.02 s-1时,动态抗压强度增加至159.27 MPa,增加幅度为13.54%;应变率为75.07 s-1时,动态抗压强度增加至167.99 MPa,增加幅度为5.47%;应变率为84.87 s-1时,动态抗压强度增加至181.34 MPa,增加幅度为7.95%;应变率为99.07 s-1时,动态抗压强度增加至195.36 MPa,增加幅度为7.73%。

分析认为,岩石的变形破坏是内部缺陷萌生与扩展的最终结果,而缺陷产生所需的应力远大于缺陷扩展所需的应力,因此岩石需要足够的应变率作用持续产生新的缺陷使其完全破坏,表现为动态抗压强度随应变率的增加而增强,但由于冻融循环的劣化作用,增长速率有所减缓。

综合图5可以看出,冻融岩石的动态抗压强度受冻融因子与应变率因子的共同控制,但两者导致的效应相反。

4.1.3 动力变形分析

依据表1绘制不同冻融次数和应变率下岩石动弹性模量的变化曲线,结果如图6所示。

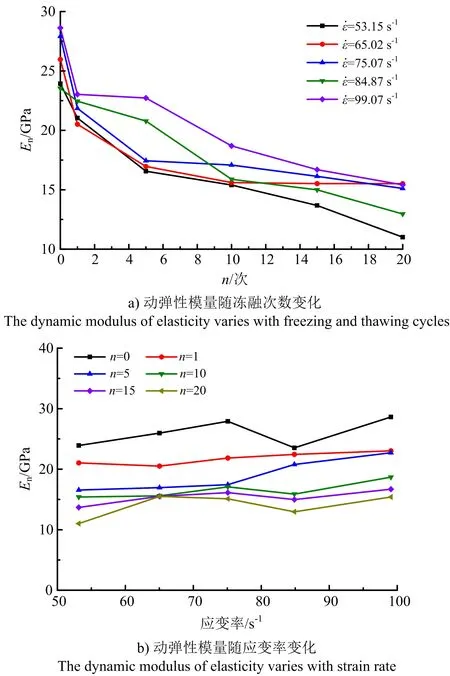
图6 动弹性模量随冻融次数、应变率变化Fig.6 The dynamic modulus of elasticity varies with freezing and thawing cycles and strain rate

由图6a可知,随冻融次数的增加,岩石的动弹性模量总体降低,变化速率先快后慢。应变率为75.07 s-1时,冻融次数由0增加至5次过程中,动弹性模量下降60.03%;冻融次数由5次增加至20次过程中,动弹性模量下降15.42%。这是因为,冻融次数的增加使得岩石内部冻融损伤加剧,原有的微观缺陷扩展、贯通,岩石力学性能劣化,抵抗冲击变形的能力减弱。

由图6b可知,随应变率的增加,动弹性模量整体呈增加趋势,但变化幅度较小。例如,应变率由53.15 s-1增加至99.07 s-1过程中,冻融次数为0时,动弹性模量增加幅度约为16.42%;冻融次数为10时,动弹性模量增加幅度约为17.61%。分析认为,冲击荷载作用下,产生惯性力,岩石内部矿物颗粒界面快速滑移,使得岩石未能充分变形而发生破坏,导致动弹性模量变化幅度较小。

因此,岩石的动态弹性模量受冻融作用和应变率作用的共同影响,但两者导致的结果不同,且动弹性模量的应变率敏感性较小。

4.2 损伤演化特性分析

为分析岩石的损伤演化特性,明确冻融损伤与动荷载损伤的耦合效应,根据表1及式(10)绘制冻融岩石的动态损伤演化曲线,结果如图7和图8所示。

图7 不同冻融次数下岩石的损伤演化Fig.7 Damage evolution of rock at different freezing and thawing cycles

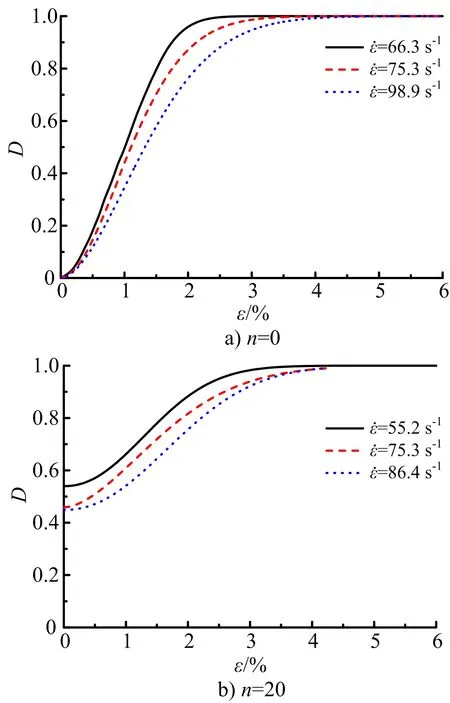
图8 不同应变率下岩石的损伤演化Fig.8 Damage evolution of rock at different strain rates

从图7和图8还可以看出,随着应变的增加,总损伤值逐渐增大,从初始值趋于临界值1,损伤曲线近似呈“S”型演化,能够反映岩石动态变形破坏全过程:①初始损伤阶段,对应压密及弹性变形阶段。曲线形态近似水平,此时岩石的变形以原始缺陷压密和闭合为主,无明显新生缺陷产生。②线性损伤阶段,对应塑性屈服阶段。随应变的增加,损伤演化曲线呈近似线性,说明此时岩石内部损伤稳定发展,产生不可恢复变形,总损伤值增加;③非线性损伤阶段,对应应变软化阶段。损伤演化曲线增长速率减缓,呈上凸形态,说明此时岩石内部裂纹、孔隙的聚合与贯通产生了新的宏观断裂面,承载能力降低。④损伤破坏阶段,损伤演化曲线逐渐平缓,总损伤值接近1,此时岩石承载能力丧失,应力瞬间释放,产生破坏。

图7显示,在变形初期,随冻融次数的增加,损伤曲线的演化速率逐渐变缓,总损伤值与冻融次数呈正相关。在变形中期,损伤曲线依次相交,相交后总损伤值与冻融次数呈负相关,图中表现为损伤值一定时,应变随冻融次数的增加而增大,发生破坏时所对应的应变也越来越大。说明岩石的冻融-动荷载的耦合作用对总损伤有所弱化,且弱化程度随着冻融循环次数的增加而增大。这是因为岩石在变形后期表现出了较为显著的塑性特征。

图8显示,相同应变时,总损伤值随应变率的增加依次减小,说明岩石抵抗动力变形破坏的能力有所增强。这是因为冲击荷载产生的惯性力导致岩石处于被动围压状态,内部微缺陷得到压密、闭合,力学性质有所改善,表现出应变率强化效应。此外,应变率增大,岩石损伤演化速率减缓,达到临界破坏的过程有所延长,表明此时岩石的塑性特征较为明显,岩石需要足够的冲击作用使其内部缺陷持续扩展、萌发,最终完全破坏。

5 模型验证

根据表1的试验数据,由式(13)及式(33)～式(34)进行计算,绘制不同冻融次数及应变率下岩石的σ-ε理论曲线(见图9),并与文献[14]的试验曲线进行对比。可以看出,冻融岩石动态损伤本构模型理论曲线与试验曲线能够较好地描述不同冻融次数及应变率下岩石的变形破坏过程,反映其动载强度和变形特征,验证了损伤变量、模型参数及本构方程的合理性。

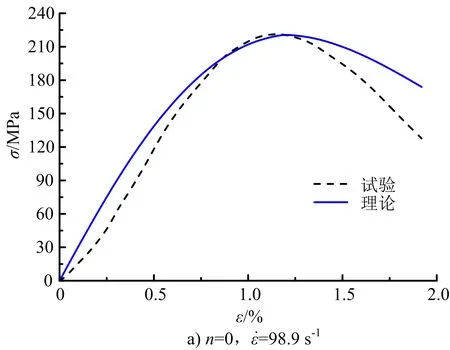
图9 砂岩损伤模型理论与试验比较Fig.9 Comparison between test and theoretical of constitutive model for sandstone

6 结论

1)基于岩石SHPB冲击压缩变形破坏全过程,考虑岩石材料的非均匀性质,基于统计损伤理论,将岩石弹塑性和应变软化特征概化为损伤特性,应变率效应描述为黏滞性,建立冻融岩石动态损伤本构模型,理论表征冻融损伤与荷载损伤的耦合效应及其诱发的宏观力学响应,并确定模型参数的理论表达式。

2)岩石抗冻系数随冻融次数的增加,呈减小趋势,冻融前期,抗冻系数随应变率的增大而降低,但随冻融次数的增加,不同应变率下抗冻系数曲线相继相交,相交后抗冻系数随应变率的增大而增加。岩石动态抗压强度与冻融次数呈负相关,冻融初期变化显著,之后变化幅度基本稳定;与应变率呈正相关,变化速率先快后慢。岩石动弹性模量随冻融次数增加而降低,随应变率增大整体呈增加趋势,变化幅度较小。所以,动态抗压强度与动弹性模量受冻融作用和应变率作用的共同影响,但两者导致的效应不同,且动弹性模量的应变率敏感性较小。

3)随应变的增加,损伤曲线近似“S”型演化,总损伤值从初始值趋于临界值1,较好地反映了冻融岩石动态变形破坏全过程。应变率一定时,总损伤值随冻融次数的增加而增大,但在变形的中后期,随冻融次数的增加而减小,表现出明显的塑性特征;冻融次数一定时,应变率的增加,导致岩石处于被动围压状态,力学性质有所改善,总损伤值依次减小,表现出了应变率强化效应。