爆炸荷载作用下不同形式采空区损伤模式研究
2023-11-02郭连军汪旭光李广尚徐振洋闫大洋
潘 博,郭连军,汪旭光,李广尚,徐振洋,闫大洋
(1.鞍钢集团北京研究院有限公司,北京 102209;2.辽宁科技大学矿业工程学院,辽宁 鞍山114051;3.沈阳工业大学建筑与土木工程学院,沈阳 110870;4.矿冶科技集团有限公司,北京 100160;5.鞍钢矿业爆破有限公司,辽宁 鞍山 114046)
由于历史原因,鞍钢集团矿业有限公司辖属齐大山、弓长岭等露天矿山、遗留了诸多采空区,加之区域矿产资源未集中整合前的不规范开采,进一步增加采空区的数量。采空区的塌陷、涌水和边坡失稳成为矿山主要地质灾害之一,给矿山设备和人员的安全带来严重的威胁,其处理方案的选择直接影响到矿山开采的经济效益和生产效率,因此,选用何种方式对采空区进行处理显得极为重要。解治宇等[1]对于多层采空区采取分层、分区爆破处理的技术方案,使弓长岭露天矿大砬子采场采空区得到了有效治理。黄英华等[2]基于模糊数学理论和层次分析法,建立了采空区稳定性评价指标体系,计算结果可为后期采空区治理及监测提供参考。解联库等[3]通过采用类比法、力学理论计算以及极限平衡法校核等,确定了隐伏空区预处理顶板安全厚度,形成了一种空区顶板安全厚度的综合判别法。辛文彬等[4]在充分调研矿山开采现状的基础上,通过调整起爆顺序,增加单位时间内的爆轰能量,实现了采空区与矿柱协同爆破治理,消除了采空区顶板垮塌风险。彭超等[5]通过采用类比法、力学理论计算以及极限平衡法校核等,确定了隐伏空区预处理顶板安全厚度,形成了一种空区顶板安全厚度的综合判别法,使采空区治理综合利用得到了极大改善。方翔等[6]借助钻孔式三维激光扫描技术,充分掌握地质信息,实施了无侧向自由面采空区爆破治理,消除了采空区的事故隐患。
结合露天矿山的生产特点,相对经济合理的采空区治理方案为爆破崩落处理。但由于实际采空区的分布形态各异,增加了该问题的研究难度,相似模型试验[7]可以很好地解决这个问题,但若以“一区一模”的方式进行分析,得到的结果适用范围有限。因此,本研究根据实测结果简化采空区形貌,依据岩体的性质制备相似模型并进行爆破试验,了解在爆炸作用下采空区顶板的整体响应特征,揭示在爆炸荷载作用下采空区的损伤破坏模式,损伤分布破坏关键区,为采空区爆破处理方案优化提供技术支撑。
1 相似模型原理及试件制备
1.1 采空区形态简化
露天矿既有采空区具有边界复杂、形态不规则的特点(见图1),相似模型的制作难度较大,而其稳定性问题属于概率范畴,引入蒙特卡罗方法[8]可以很好地解决模型制作难题。其特点是通过曲面间的布尔运算构建几何栅元,进而组成实体模型,可以处理绝大多数任意几何模型,即为构造几何实体过程。通过逻辑运算,利用基础几何体完成复杂曲面或者几何体的构建,因此,理论上露天矿山开采过程中涉及到的所有采空区,都可以通过基础几何体的构造运算完成其复杂呈现形态的构建。本文空间几何体的重组,采用长方体、圆柱体、三棱柱作为体元,使用布尔运算组合在一起,逻辑运算符包括交集、并集以及差集或补集,其以空区空间体左视某截面轮廓线为例进行演化组合,如图2所示。
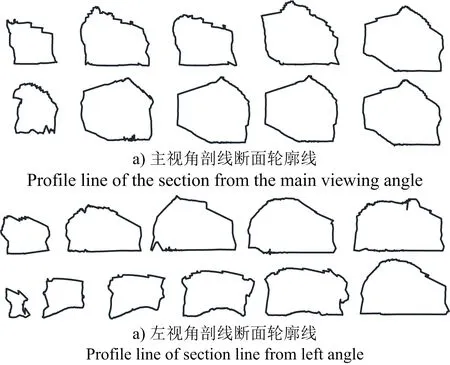
图1 采空区断面轮廓线Fig.1 Profile line of goaf section

图2 逻辑运算符及重组构线Fig.2 Logical operators and recombination constructs
通过几何体元的空间位置组合,可以实现对采空区的重构,但这里还需作一个假定,以解决结构的等效力学问题,即构成复杂空区体的基本几何体元受到荷载的响应效果与原空区近似相等,且原空区的宏观表征视作各组成部分宏观表征的组合。这里将预处理采空区近似看作与对应的体元具有自相似性,借鉴有限元思想,把复杂的采空区结构离散成有限个规则的体元空间,假定每一个体元在爆炸荷载下的应变具有独特性,然后通过体元的应力-应变状态来把握采空区整体变化趋势。基于上述假设,为方便讨论,本文验证某一局部空间区域可以通过体元运算构成。由于采空区具有自相似诸多学者已经有了大量的论证[9-10],基于此将二维平面拓展至三维体,那么以某部分采空区为例,进行空间体的三维重构如图3所示。经过多个基础空间体组合运算后,即可组成目标空间体,同样采空区的整体空间形态,也可以通过上述方法分解成多个相似单元体,这样复杂的空区体损伤问题则可转化为研究简化后单元体的损伤问题。
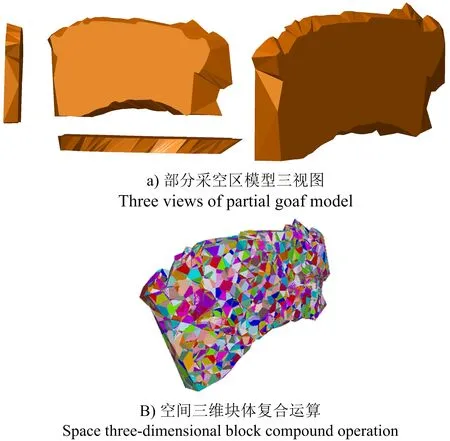
图3 空区三维形态重构Fig.3 Three-dimensional morphological reconstruction of goaf
1.2 相似理论分析及试件制备
1.2.1 材料相似性分析
将爆破试验中涉及影响因素进行整理,根据相似理论π定理,将n个的因素进行归一化,无量纲化处理,可得:
f(π1,π2,…,πn-k)=0
(1)
式中:π1、π2、…、πn-k为无量纲量。
根据国际计量大会建议[11],对于采空区爆破处理,选取力(F),长度(L),时间(T)为独立量纲。结合试验最终目的找寻在爆炸作用下,空区破坏的关键位置,为工程设计提供参照,力求在工程实际中处理空区达到顶板塌落程度高,且尽可能减少炸药使用,因此主要针对几何相似、材料相似和炸药性质相似进行分析,所选参数如下:
几何相似包括,空区的简化三向尺寸长A(m),宽B(m),高H(m),顶板厚度H1(m),隔板厚度H2(m),炮孔深度h(m)。材料相似包括,密度ρr(kg/m3),弹性模量E(GPa),波阻抗ρrC(kg/m2s),抗拉强度σ(MPa);炸药性质相似包括,密度ρe(kg/m3),炸药爆速D(m/s),炸药单耗Q(kg/m3)。关键位置点:(x,y)将以上物理量,用所选定的量纲表示,如表1所示。
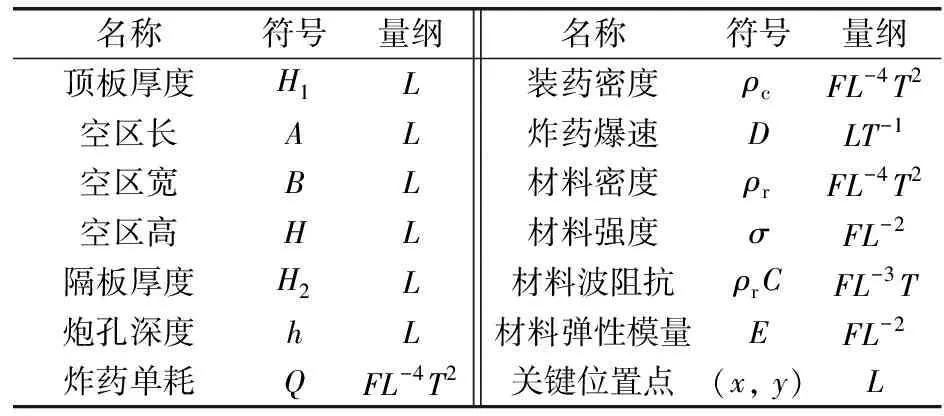
表1 模型参数及量纲
根据相似理论第二定理,将表1中所涉及的既有采空区爆破处理效果各参数表示成下式形式:
f(H1,A,B,H,H2,h,Q,ρc,D,ρr,σ,ρrc,E,(x,y))=0
(2)
设各模型参数的指数为a1,a2,…,a13,则指数与量纲关系如表2所示。

表2 参数指数与量纲关系
将h、ρc、D作为基本参数,即表2中a6,a8,a9,解该系数矩阵方程式,可得:
(3)
将其余a1,a2,a3,a4,a5,a7,a10,a11,a12,a13设为变量,当指定其中ai(i=1,2,…,5,7,10,11,12,13)为1,剩余9个变量为0,则各相似准数分别为
(4)
那么有:
(5)
由式(5)可知有10个影响空区爆破处理效果的因素,其中几何参数为π1、π2、π3、π4,这说明在处理方案上要充分考虑空区的几何特征,π5揭示了对于有隔板的空间平面投影重叠的多层采空区,炮孔深度对隔板的处理有一定影响,二者之间有一定关联,但实际中对于隔板进行钻孔,往往需要套筒作业,难度较大,因此可以考虑集中药包与钻孔相结合的方式,减少隔板的钻孔作业。π6、π8说明空区顶板物性特征及炮孔深度对处理方案的影响。一般来说,顶板的承载力好,有利于设备作业,当顶板承载力足够大,且不影响生产进度时,可以适当考虑延缓空区的处理,但需要对顶板实施长时监测,当强度临近破坏阈值时及时进行处理。需要指出的是炮孔的布设要充分结合地探资料,在炮孔布设时,避免非必要的顶板穿透。π7、π9、π10则说明被爆矿岩介质与炸药的波阻抗匹配情况对爆破效果的影响。应力波对矿岩的作用情况,直接影响着最终作用效果。根据以上分析可知,保证以上量纲中10个量纲一致,选用混凝土进行相似模型制作,则需满足相似比:
(6)
式中:角标1为模型,0为模拟参照对象。
由于模型尺寸远小于实际,为保证试验效果,参照以往经验,选择单质猛炸药进行试验,更有利于匹配被爆介质与炸药的波阻抗[12],文中采用导爆索(黑索金)开展研究。
1.2.2 试件制备
混凝土相似配比参照围岩静力学性质,根据文献[13]及工程经验进行3种配比试件与原岩对比,如图4所示。最终选用配比方案1,即水∶52.5R普通硅酸盐水泥∶硅粉∶砂石骨料为1∶4.2∶0.3∶10.5的比例进行配比,并加入水泥量3%的早强剂,并在常温条件下保水养护,得到最终的试验试件。
以1 m3为基准量,以等体积三棱柱、长方体为既定空区,具体设计如图5所示。双层空区模型保证隔层最小距离相等进行浇筑,单一三棱柱空区体积约为0.083 m3,长方体空区体积约为0.081 m3,预留顶板厚度为300 mm,炮孔位于试件上表面中心位置,炮孔深度为200 mm,炮孔直径46 mm,双层空区隔板厚度为100 mm。

图5 模型设计与试件实物Fig.5 Model design and physical specimen
2 三维数字图像原理及试验过程
由于爆破的瞬间都是高速作用,传统的手段很难监测劈裂的位置,因此需要高速相机去拍摄整个爆炸过程,持续时间仅为几秒钟,利用三维全场重建解算基于数字图像相关方法(3D-DIC),可通过追踪物体表面的散斑图像,实现被监测目标在变形过程中其表面三维坐标、位移及应变的动态测量。其原理是在被测目标选定基准子区域,其中心坐标为(x0,y0),当荷载作用过程中该区特征信息(如灰度值)不发生变化,基于此荷载作用结束后,在所拍摄的影像中根据找出这一基准子区域以及其中心坐标(x1,y1)即可得到该基准区域的位移量(见图6),这样对摄影视野内其余点进行上述计算便可获得被测目标整体变化信息,同理对其他变化指标进行分析,最终能够获得被测目标的全场位移和应变情况。
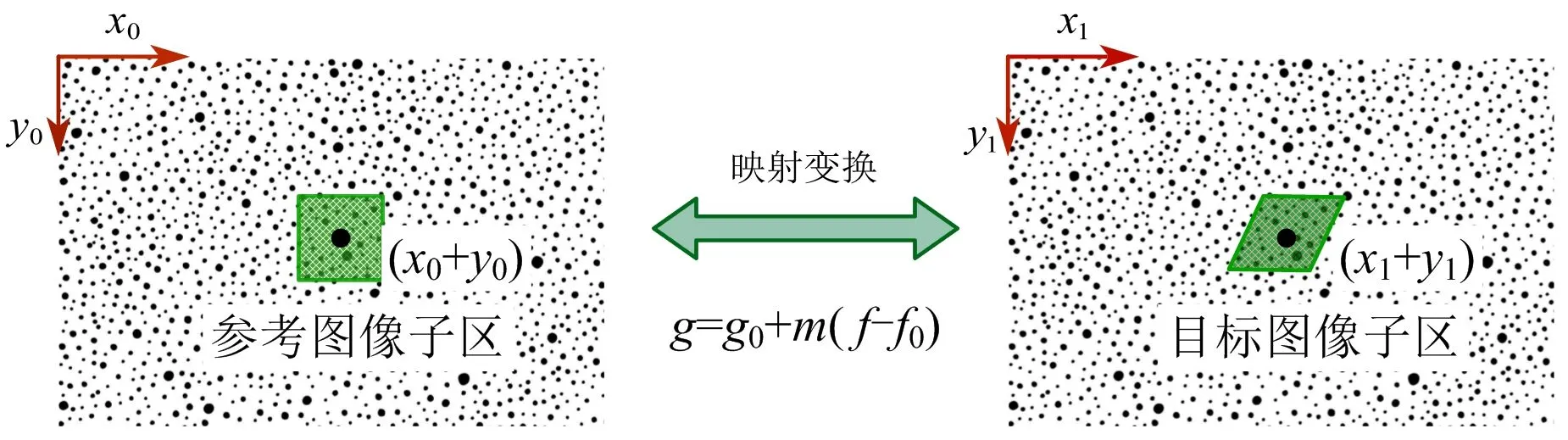
图6 种子点匹配Fig.6 Seed spot matching
2.1 相机自标定
自标定实际上是试验场标定的一种特殊情况,如果试验场内的控制点的数目为0,所有的物体点的坐标都是未知的。故需明确空间内某一点位信息,然后基于光束平差原理,经过换算即可得出同一三维坐标系中摄影机内、外参数以及被测目标的坐标信息,如图7所示。
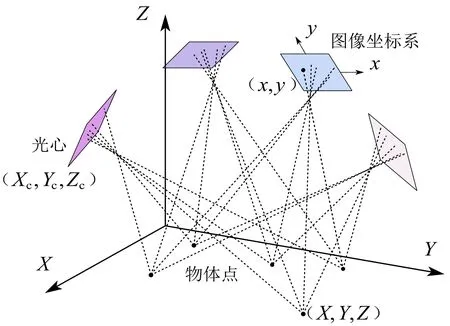
图7 摄影测量原理Fig.7 Photogrammetry principle
对于不同焦距的镜头拍摄图像所产生的畸变规律不同,直接导致最终标定精度的差异,基于此,提出参数畸变模型:
V=AX1+BX2+CX3-L
(7)
式中:V为像点坐标残差;X1,X2,X3分别为内方位参数、外方位参数和被拍摄物方位坐标的改正数;A,B分为内、外方位参数;C为被测体坐标所对应的偏导矩阵;L为图像点坐标。
对于上述方程,若已知内、外方位参数求被测目标体坐标,那么误差方程可简化为
V=CX3-L
(8)
同理,若已知被测目标体的点坐标及内方位参数求外方位参数,误差方程则可简化为
V=BX2-L
(9)
上述3种计算模型,求解过程是多参数非线性优化的过程,所涉及的内、外方位参数以及被测目标体的三维信息在被不断优化,直至达到较为理想的精度。
2.2 试验流程
2.2.1 喷涂散斑
以双层长方体模型为例,首先需对材料表面进行抛光处理,并粘贴散斑标记点,散斑点利用哑光黑自喷漆完成喷涂,喷涂密度为测量区域的70%,如图8所示。

图8 散斑标记点Fig.8 Speckle marking point
2.2.2 相关位置计算及标定
根据三角形成像原理,如图9所示,对高速相机位置定位及相关尺寸进行确定,具体可根据式(10)进行计算,可以求解出相机的摆放位置。
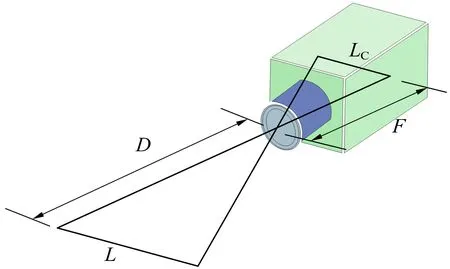
图9 三角形成像原理Fig.9 Principle of triangle imaging
D=FL/LC
(10)
式中:L为测量幅面;F为焦距;D为测量距离;LC为相机靶面尺寸。
试验相机分辨率为1 064×768,搭配50 mm固定焦距镜头,靶面尺寸为13.5 μm,测量幅面为1 000 mm×1 000 mm,解得D为3 496.5 mm,即相机摆放位置距试件的距离,如图10所示。

图10 相机布设Fig.10 Camera layout on site
对镜头焦距及光圈进行调节,确保各个标定点对象在采集观测窗口显示清晰,若出现图像不符合要求即图像拍摄不全或者编码点没有全部识别,可以在图像列表中对相应的图像点进行删除重新采集。所用的标定板如图11所示,各个标志点之间的距离为未知量,以对角线上一对编码点的距离作为比例尺。

图11 模型试验现场标定Fig.11 Field calibration of model test
2.2.3 装药起爆及数据采集处理
对被测试件进行装药,填塞。对照矿山炸药单耗0.22 kg/t核算,由于试验目的为观察爆炸作用下,裂纹发育及各个形态空区顶板的应力场变化,找寻应变关键区域,因此试验采用孔内双发8号雷管附10段10 cm导爆索,合计药量为11.7 g/m3,采用不耦合装药,炮泥填塞,如图12所示。

图12 装药及填塞Fig.12 Charging and packing
起爆时刻触发拍摄快门,两台相机实时拍摄爆破过程的二维图像。数据采集后,将爆炸过程中的图像序列导入软件内进行计算,创建散斑块即计算域,系统仅对散斑域内的点进行计算和三维显示。最终经过种子点创建后,计算出散斑标记点的三维坐标值,进而解算出应变场、位移场。
3 结果与讨论
对试验采集到的图像进行处理,可得出拍摄过程中每个试件在爆炸荷载作用下X、Y、Z3个方向的位移云图以及最大主应变的云图,为降低试件的边界效应影响,截取应力波传至拍摄面直到应力、应变最值时段进行分析。
3.1 双层长方体空区破坏过程分析
爆破开始前,试件表面基本处于稳态,炸药被引爆时由于爆炸振动作用,而发生位移沿Y向的位移(见图13)。随着应力波作用,当爆炸应力波传至信息面,顶板出现裂纹,随着应力波的持续作用,拍摄区域内散斑向右发生最大3.436 mm的位移,由于试件两边未施加约束,因此应力波在自由面会产生拉应力。同样由于裂纹的产生,增加了新的自由面,因此在整个破坏过程中会看到裂纹处会有碎块脱落。随着应力波作用,可以看到,在隔板处位移云图出现了集中高亮区。由裂纹产生至隔板发生位移,历时0.48 ms。

图13 双层长方体空区模型动态位移Fig.13 Dynamic displacement of double cuboid goaf model
在爆破作用下空区尖点处上方顶板区域,出现高应变区,说明该处为爆破作用关键点,裂纹起裂尖端也在这一区域。当顶板裂纹扩展至最大时,隔板出现应变高亮区,与顶板呈中心对称位。这说明此处为潜在断裂处,最终试件的破坏形式也验证了这一点,该过程历时0.54 ms(见图14)。对比未拍摄面的裂纹形式,可以看到隔板处出现双裂纹,与拍摄面的应变高亮区域位置对应。那么在对顶板进行爆破作业时,隔板装药设置合理的延时时间,针对裂隙区进行爆破作业,则可达到预期的崩落效果。

图14 双方体空区模型裂纹分布及应变Fig.14 Crack distribution and strain cloud of double cuboid goaf model
3.2 双三棱柱体空区破坏过程分析
从双三棱柱空区位移云图(见图15)中可以看出,顶板初始位移发生在拍摄面右侧,位移发生点处于炮孔中心片线位置。根据试验拍摄结果,可以得出,除顶板裂隙处发生明显位移外,在两空区隔板处位移云图有明显的界限,但并未出现可见裂纹,说明该处为潜在断裂区域,隔板处可能发生断裂滑移,该过程顶板裂纹处发生最大位移为3.965 mm,后续过程由于试件破碎程度较大,产生了大量烟尘导致图像无法清晰拍摄全过程,因此上述移位并非最终值。
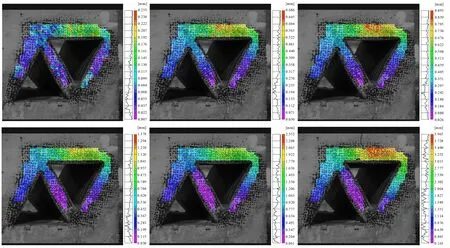
图15 双棱柱体空区模型位移Fig.15 Displacement of two-layer triangular prism goaf model
在起爆后应变由顶板两端尖点处向炮孔中心转移。爆炸应力波作用下,宏观裂纹产生时应变为1.613%。爆炸应力波持续作用下,裂纹开张程度增加,在顶板边缘尖点处及空区侧向靠近尖点处出现集中应变区。空区与空区之间的尖端连线处,将成为隔板断裂关键区域。对于侧向围岩,应变集中区随着隔板破坏关键区发生的应变变化向下方尖端转移,该过程历时0.24 ms(见图16a)可知,尽管由于烟尘原因未能捕获试件破碎全过程数据,但就目前可处理的部分数据分析来看,已充分说明该类型空区的应力关键作用区,可以得出破碎发生起始位置以及潜在的破碎区域,如图16b所示。因此在工程中若顶板结构中有较为集中的尖点分布,该区域的炮孔装药可相应减少,以达到低耗高效的作业目标。
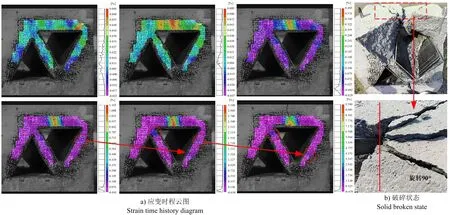
图16 双棱柱体空区模型应变云图及最终破碎状态Fig.16 Strain cloud image andfinal fracture state of double-layer tri-prism goaf model
4 结论
1)相同荷载作用下,预置的采空区结构不同其响应特征有明显差别,长方体空区试件的破坏程度远小于三棱柱体空区试件,但形成了明显的贯通裂纹。
2)采空区结构中尖点分布对裂纹的扩展有直接影响,裂纹扩展倾向于尖点区域附近,长方体空区试件顶板及隔板破裂位置均符合该特点,三棱柱体空区试件同样在结构尖点区域有明显破坏,隔板两端为结构尖点集中区域,因此破坏程度较大。
3)对工程实测的采空区,若存在投影面重合且两采空区之间有关联影响,对于处在下层的采空区顶板处理时,可设计一定延时使能量得到充分利用;若采空区顶板结构中有尖点,则该区域的炮孔装药量可适当进行调减,以达到低耗高效的处理效果。
