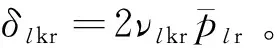刚构桥随机地震动响应的简明解析解及等效地震力计算
2023-11-02廖勇刚张梨荣葛新广
廖勇刚,张梨荣 ,葛新广
(1. 广西西江集团红花二线船闸有限公司,广西 柳州 545100; 2. 柳州工学院 土木建筑学院, 广西 柳州 545004)
0 引言
桥梁工程是各类交通工程的重要构成,其在地震过程中震害突出,影响巨大[1-3]。刚构桥适用于大跨高墩结构,广泛应用于市政、公路、铁路及轨道交通工程中[4]。为了获得更好的静力学特性,刚构桥构造上采用强梁弱墩的布置形式,与其他类型桥梁相比,因采用梁-墩固结,结构刚度大,自振频率较同跨度连续梁、简支梁高,动力响应显著。近年来,中国交通业的高速发展促进了刚构桥的工程应用,全国各地建造了众多刚构桥项目,特别在一些震区。对刚构桥地震动特性和动力响应分析是近年来工程界的研究热点[5-8]。单德山等[9]研究了断层距对大跨高墩连续刚构桥的响应特点,研究表明:不同断层距的大跨高墩连续刚构桥梁的地震响应具有明显差异,近断层地震响应明显强烈;闫晓宇等[10]基于振动台试验研究了近断层效应对刚构桥的动力响应,研究表明:近断层对刚构桥桥墩和主梁的跨中内力与位移具有显著影响。以上研究主要关注时程地震动激励下对刚构桥桥墩水平方向的动力响应分析,实际上地震动具有显著的随机性[11-12],且在顺桥向水平地震作用下,桥墩产生侧移使墩顶产生动弯矩进而引起梁跨结构的竖向震动和水平震动。因此,研究顺桥向水平随机地震动作用下,刚构桥顺桥向和竖向耦合地震效应,对于确保刚构桥抗震防灾具有理论意义。
工程上,利用功率谱密度函数描述地震激励的随机性是一种主要方法,如白噪声谱、Kanai-Tajimi谱、Clough-Pezien谱和欧进萍谱等[13-16]。基于功率谱模型的地震动响应分析,主要有时域法和频域法[17-18]。时域法中结构响应的协方差由地震激励协方差与脉冲响应函数在时域的二重积分来表示,对于白噪声激励易于获得响应的简明解,但对于其他复杂地震动谱则存在响应计算复杂的问题。频域法中,结构响应的功率谱密度函数表示为地震动功率谱密度函数与响应量频响函数模值平方的代数积,表达式简洁因而得到广泛应用,虚拟激励法是其典型代表[18]。然而结构安全评估和设计需要响应量的方差和谱矩,是基于响应量功率谱密度函数在频域上的积分。现行《公路桥梁抗震设计规范》(JTJ/T 2231-01-2020)[19]采用功率谱法计算桥梁随机地震动响应,应用时采用有效频率区间的数值积分法进行近似计算。近年来,张俊等[12]和葛新广等[21-22]针对传统方法无法获得封闭解的不足,提出了结构响应方差和谱矩计算的封闭解法,所提方法无需数值积分运算。
针对多跨刚构桥在顺桥向水平地震作用下,墩梁固结处的墩顶部产生动弯矩进而使相连的桥跨结构产生动弯矩,从而引起桥梁水平与竖向耦合振动的特征,提出了一种研究刚构桥在顺桥向随机地震动作用下,水平和竖向耦合振动位移谱矩和等效地震力的新解析解法。首先,建立刚构桥双向地震动方程,基于MIDAS有限元软件对刚构桥进行离散化建模并获得其竖向及顺桥向振动的振型、自振圆频率和节点集中质量的动力参数;其次,基于实模态解耦法,将整桥结构节点位移表示为实模态振型的线性组合;再次,基于功率谱密度函数的二次化法[21-22],获得了广义变量及节点位移响应谱矩和方差的解析解法;最后,基于动力学等效原则获得了刚构桥节点等效地震力计算式。
1 刚构桥地震动位移响应的频域解
连续刚构桥的结构形式为边墩与桥跨结构采用支座连接而中墩与桥跨结构采用刚性连接,动力学上常采用集中质量法进行结构离散化如图1所示。顺桥向地震动作用下桥墩的墩顶会产生动弯矩从而引起桥跨结构产生动弯矩,进而引起桥跨结构产生顺桥向及竖向振动。为此,考虑全桥结构顺桥向水平及竖向振动自由度建立其动力方程为:

图1 刚构桥动力学简图Fig. 1 Dynamic calculating diagram of rigid frame bridge
(1)
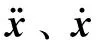
引入广义坐标向量q,则刚构桥节点位移向量表示为[23]:
x=φq
(2)
式中:q={q1,…,qN}T, φ为刚构桥结构前N阶振型,为n×N阶矩阵。
把式(2)带入式(1)并利用实模态振型分析法,则基于广义坐标地震动方程为:
(3)
由虚拟激励法[18],式(3)所表示的广义坐标的频域解为:
(4)
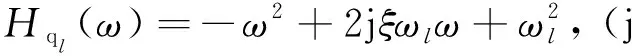
由式(2)及式(4),刚构桥i节点处位移xi的频域解为:
(5)
式中:φi,l为结构实模态振型φ的第i行和第l列元素。
2 刚构桥响应功率谱的二次分解式
由式(4)及虚拟激励法[18],广义坐标响应功率谱表示为:
(6)

由式(4)可知:对式(6)中的|Hql(ω)|2式进行二次式分解,即:
(7)
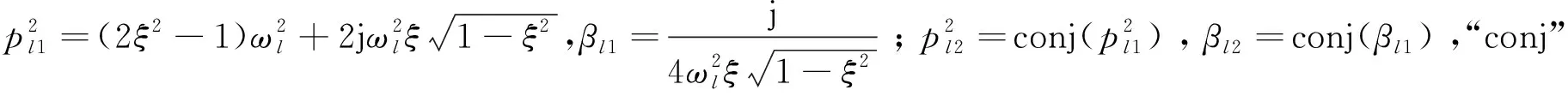
把式(7)带入式(6),则广义坐标的功率谱表示为:
(8)
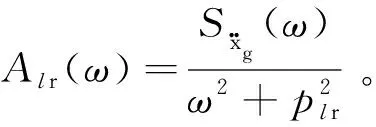
由式(5)及虚拟激励法[18],则位移响应的功率谱表示为:
(9)

对式(9)进行求和展开:
(10)
(11)
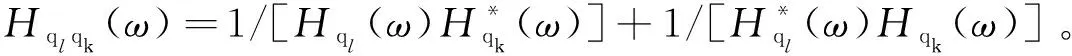
针对Hqlqk(ω)进行二次式化,具体见附录A,其二次式为:
(12)
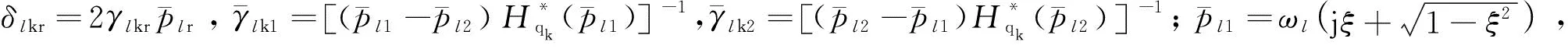
由式(11)和式(12),结构位移响应功率谱表示为:
(13)

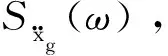
(14)
式中:ξf,ξg,ωf,ωg分别为场地土的振动特征值,S0为地震动强度系数。
由留数定理,对式(14)进行二次式分解为[23]:
(15)
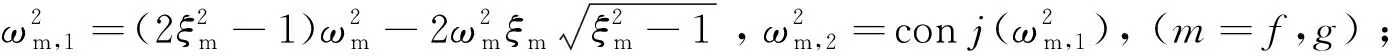
3 结构响应谱矩和方差的简明封闭解
由随机振动理论[17-18],刚构桥位移响应和广义变量的谱矩和方差表示为:

(16)
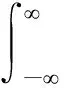
(17)
(18)
把式(8)带入式(16)及式(13)带入式(17)并进行积分,谱矩表示为:
(19)
(20)
式中:
(21)
(22)
对式(21)和式(22)进行积分,可获得其解析解为:[23],
(23)
(24)
(25)
(26)
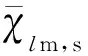
4 等效地震力的计算
工程设计常需要获得结构地震动作用下的内力,以便与静荷载工况结构内力进行荷载组合。在获得随机结构动位移方差的基础上,利用惯性力和动力学原理可获得等效的节点地震力,是一种拟静荷载,便于获得地震作用下结构的内力值。
由结构动力学可知[24]:线弹性结构实模态解耦时,满足下式:
(27)
基于式(27)、式(28)、式(29)和式(30),可获得结构体系无阻尼自振圆频率ω和实模态振型φ。
由随机振动理论[17-18],广义变量二阶导数标准差与广义变量标准差存在关系为:
(28)
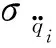
由式(2)和式(28)可知: 第i阶振型的节点位移标准差向量可表示为:
(29)
式中:σxi和φi分别为第i阶振型节点位移方差向量和第i阶振型。
惯性力可表示为质量与加速度的乘积,故节点惯性力向量可表示为:
(30)
在结构体系确定时,由结构力学的位移法可知,节点力可使结构体系产生确定性节点位移;反之,当确定性节点位移已知,可反推出确定的节点力,
σFi=Kσxi
(31)
由式(27)、式(30)及式(31),结构体系节点力标准差可表示为:
(32)
工程设计时,结构设计响应值取峰值因子与响应量标准差的乘积,故第i振型的刚构桥等效地震力可取:
(33)
式中,FE,i,cf为节点等效节点地震力向量,cf为峰值因子,《公路桥梁抗震设计》规范(JTJ/T 2231-01-2020)[19]取2.5。
利用式(33)可结构实模态振型对应的节点等效地震力,并利用有限元软件获得结构等效内力,可SRSS法获得多振型下的地震等效内力设计值。
5 算例
某3跨预应力混凝土连续刚构桥(跨度布置为60 m+110 m+60 m),采用变高度单箱单室截面,最大梁高7.0 m,最小梁高3.0 m,如图2所示。1#墩和4#墩采用矩形实心墩(2 m×9 m),高分别为16.5 m和17.5 m;2#墩和3#墩采用净距为1.3 m的双薄壁墩(1.3 m×9 m),高分别为20.5 m和21.0 m。按8度设防,场地土为中硬土,双过滤白噪声激励参数:ωg=15.71 rad/s,ωf=0.4ωg,ξg=ξf=0.72,S0=111.34×10-4m2s-3。
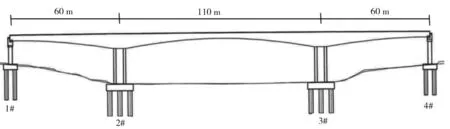
图2 刚构桥动力学简图Fig. 1 Dynamic calculating diagram of rigid frame bridge
利用Midas软件对刚构桥进行有限元离散化可获得刚构桥的实模态振型和圆频率。边墩1#墩和4#墩与桥跨结构采用球形橡胶支座进行连接,模拟时边墩与主梁采用弹性连接,侧向刚度取值为450 kN/m。刚构桥结构阻尼采用瑞雷阻尼,阻尼比取5%。
5.1 所提方法验证
虚拟激励法广泛应用于各类工程的随机动力响应分析[18],是目前分析随机激励下结构动力响应最常用的方法。该方法在计算结构响应0~2阶谱矩和方差时,需要数值积分。为了验证本文方法的正确性,利用虚拟激励法及数值积分进行验证。
图3-8为采用虚拟激励法和本文方法计算桥跨结构竖向地震动和桥墩结构水平向地震动的0~2阶谱的对比图。虚拟激励法的ωu经过试算取1000 rad/s,而Δω经过试算分别取2.5 rad/s,1.0 rad/s,和0.1 rad/s。
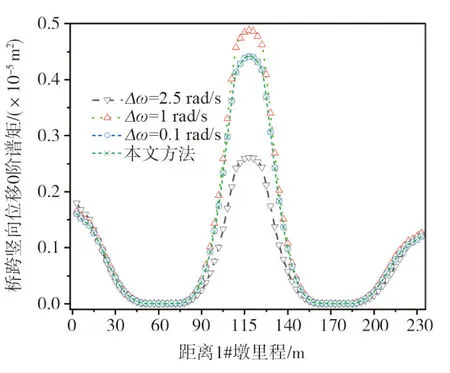
图3 桥跨结构竖向位移0阶谱Fig. 3 Zero-order spectral moments of bridge displacement in vertical direction
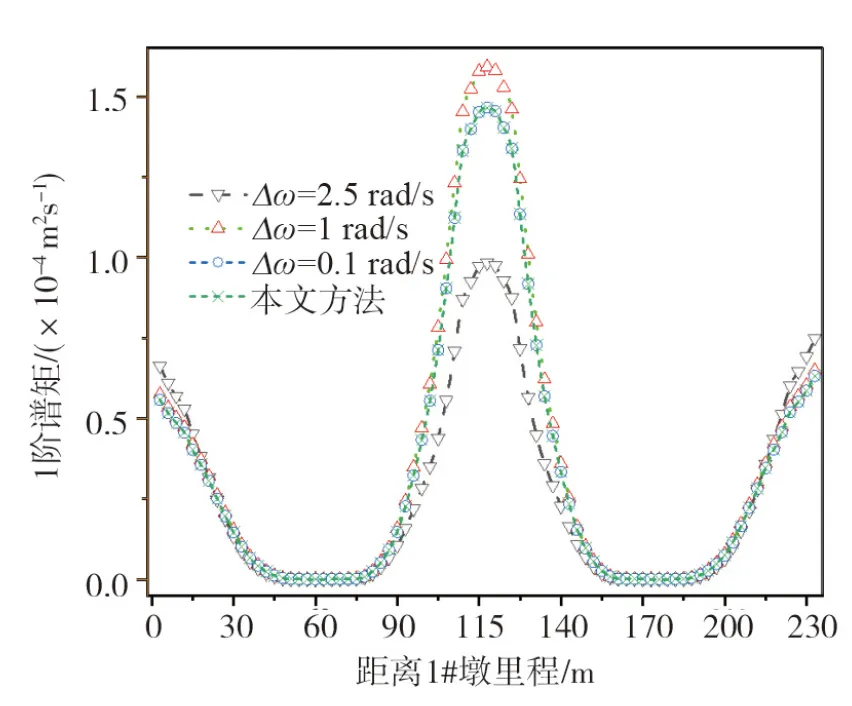
图4 桥跨结构竖向位移1阶谱Fig. 4 First-order spectral moments of bridge displacement in vertical direction
从图3-8可知:随着虚拟激励法中积分步长的变小,其计算结果越来越接近本文方法,从而说明了本文方法的正确性。虚拟激励法中Δω=0.1 rad/s与本文方法的结算结果十分吻合,在相同的计算机环境下,耗时为36.38 s;而本文方法耗时为1.06 s,说明本文方法无需试算且具有较高的效率。
从图3至图5可知:桥跨结构竖向地震动位移0~2谱矩,中跨的跨中最大;1#墩和4#墩处位移谱矩比边跨跨中位移谱矩大很多。

图5 桥跨结构竖向位移2阶谱>Fig. 5 Second-order spectral moments of bridge displacement in vertical direction
从图6至图8可知:2#和3#薄壁墩的两分支墩顺桥向位移谱基本相同,说明在桥墩构件高度相同时,可认为结构的地震动响应相同;对比0~2阶谱中边墩与中墩的位移谱矩关系,发现边墩0~1阶谱矩相对中墩较小,而2阶谱矩的边墩接近中墩,由于位移的2阶谱矩代表节点地震动速度响应量,说明边墩地震动位移较小,但其振动的速度可能会很大。
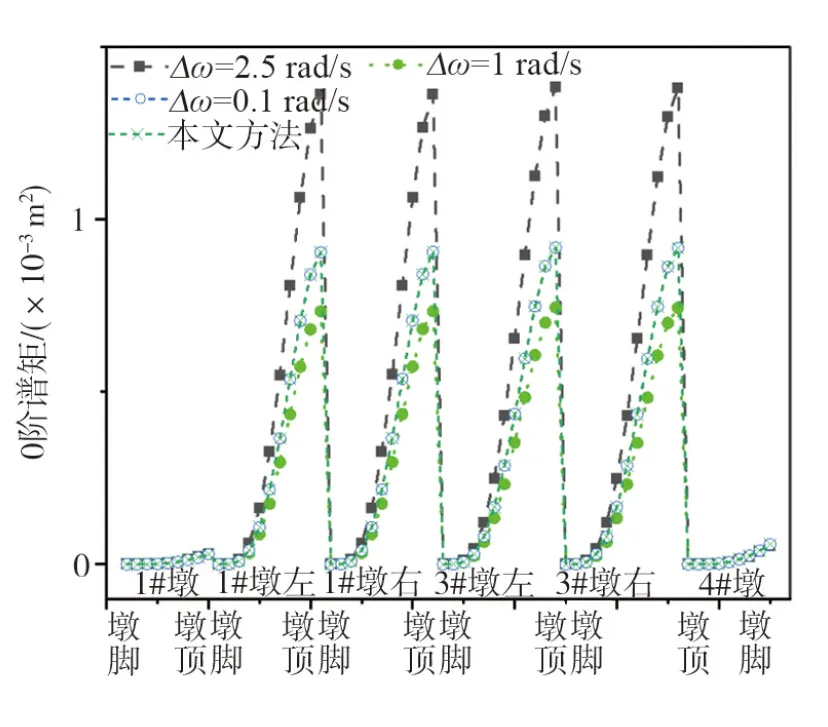
图6 桥墩结构顺桥向位移0阶谱Fig. 6 Zero-order spectral moments of longitudinal bridge displacement of piers
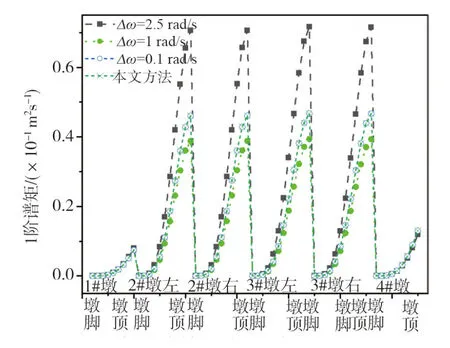
图7 桥墩结构顺桥向位移1阶谱Fig. 7 First-order spectral moments of longitudinal bridge displacement of piers
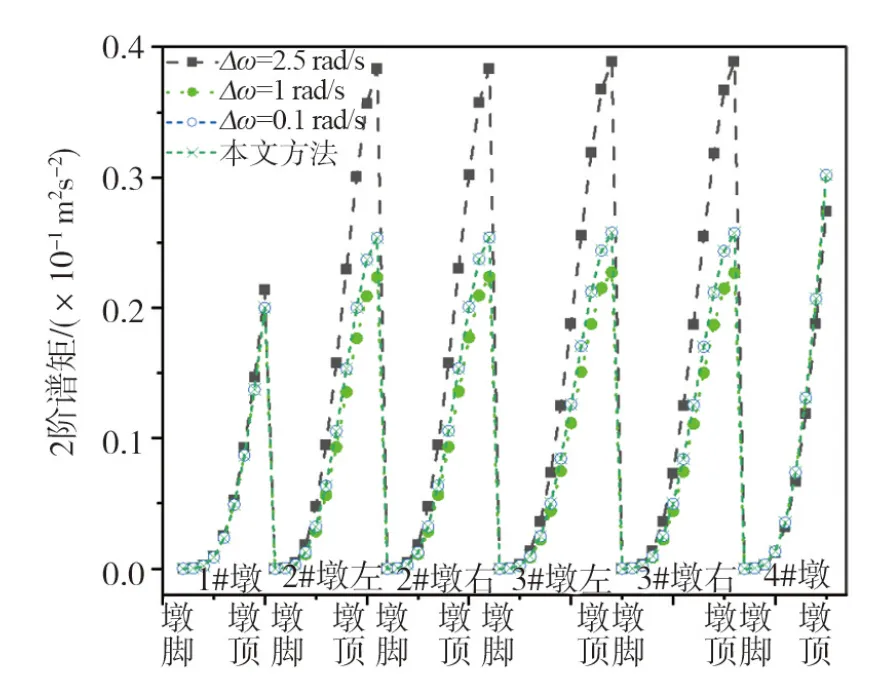
图8 桥墩结构顺桥向位移2阶谱Fig. 8 Second-order spectral moments of longitudinal bridge displacement of piers
5.2 等效地震力计算
利用式(33)计算刚构桥桥跨基于前50阶实模态振型的水平及竖向等效地震力,如图9-10所示。
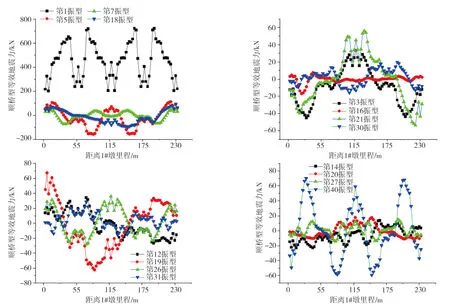
图9 基于实模态桥跨结构顺桥向等效地震力Fig. 9 Horizontal equivalent seismic forces of bridge span structure based on real model
图9及图10分别列出了对梁跨结构顺桥向震动起主导作用的16个实模态振型对应的等效地震力,顺桥向震动与水平向震动的主动振型各不相同,其中顺桥向最高阶主导振型为第40阶,竖向最高阶振型为第28阶,说明刚构桥桥跨结构地震动响应分析均需要考虑高阶振型。对比分析图10,桥梁结构竖向地震力数值较大,不能忽略。

图10 基于实模态的桥跨结构竖向等效地震力Fig. 10 Vertical equivalent seismic forces of bridge span structure based on real model
综上所述,针对刚构桥地震响应的分析,需考虑多振型的影响,且桥跨结构的竖向振动不能忽略。
6 结论
论文研究了大跨度刚构桥在顺桥向地震动作用下,双向地震动响应谱矩和方差的解析解及等效地震力的计算方法,取得了如下结论:
1)在获得各节点等效地震力方差后,利用结构力学的方法获得全桥结构的弯矩、剪力及轴力等内力,然后利用SRSS方法可获得刚构桥构件等效地震力作用下的内力值,并可与作用在桥梁上的其他荷载作用下的内力进行组合,从而可开展基于随机振动理论的桥梁结构抗震分析及动力可靠度分析。
2)针对刚构桥在顺桥向地震动作用下会产生顺桥向水平和竖向地震动效应,两种振动必须都要考虑;若采用实模态分解法进行地震动响应分析时,必须考虑多振型才能获得正确解。
附 录AHqlqk(ω)的二次式分解
针对Hqlqk(ω)进行整理:
(34)
由留数定理,式(34)可改写为:
(35)
(36)
由于pl1是Hql(pl1)的根,所以式(36)改写为:
(37)
对式(37)进一步简化为:
(38)
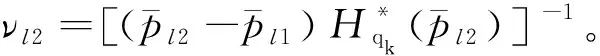
(39)
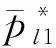
(40)
对式(40)进一步简化为:
(41)
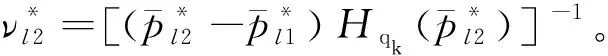
(42)
由式(42)及式(35)改写为:
(43)
对式(43)整理后,则式(35)的二次式表示为:
(44)