盾构隧道下穿河流段地震响应数值分析

2023-11-01张继清齐春雨郭景琢马庆伟

世界地震工程 2023年4期

周强,张继清,齐春雨,郭景琢,马庆伟

(1. 中国建设基础设施有限公司,北京 100089; 2. 中国铁路设计集团有限公司,天津 300308;3. 城市轨道交通数字化建设与测评技术国家工程实验室,天津 300308)

0 引言

近年来,随着城市化水平的提高,以及对地下空间开发及交通设施的需求增加,我国地下轨道交通迅猛发展;与此同时,在隧道工程的建设过程中,难免会遇到下穿河流湖泊的情况[1-2]。1985年的墨西哥Michoacán大地震以及1995年的阪神大地震,水下盾构隧道都出现了极大程度的损伤以及开裂[3-4]。

耿萍等[5]利用三维有限元手段建立了水下三维有限元模型,研究了隧道的纵向抗震性能;陈贵红[6]采用动力分析方法,对沉管隧道的动力响应进行了分析,发现地下水是地震作用增强的主要原因;然而两者研究均适用于浅埋隧道,且土层性质较为简单。

沙明元等[7]利用有限差分软件,选取了水下较为复杂的典型土层断面,模拟地震作用中盾构隧道及周围土体的地震响应,然而研究只考虑了单一地震波,同时并未指出盾构隧道中具体的加固方式;陈国兴等[8]以汕头海湾海底隧道为例,考虑了盾构隧道-竖井连接部位的三维非线性反应特性,从机理上解释了水下隧道发生震害的原因。

在以上研究基础上,本文以天津某地铁区间下穿河流段盾构隧道为例,采用Flac3D有限元分析方法[9],对盾构隧道在地震作用下的应力反应规律,相对水平位移以及加速度水平位移进行分析。在此基础上,对不同地震动幅值下的变形率进行验算。该研究成果可为盾构隧道下穿河流段的抗震设计提供有效依据。

1 三维有限元数值模型

1.1 模型建立

以天津地铁2号线某盾构隧道下穿河流段为研究对象,隧道衬砌外径6 m,内径5.4 m,衬砌厚度0.3 m,隧道上覆土厚度为7.6 m;为更好模拟该段盾构隧道在地震下响应,选取该段隧道附近一个具有代表性的天津软土场地土层作为数值计算土层分布,工程场地参数见表1。

表1 典型土体钻孔剖面参数Table 1 Typical borehole profile parameters of soil

数值计算采用有限差分法程序FLAC3D,其中模型宽度为80 m,岸坡高度为10 m,隧道顶面距河床表面7.6 m,隧道地面距模型底部30 m,模型长度共为150 m,其中穿越河道长度为90 m,双线隧道间距为25 m。地基土和隧道均采用六面体实体单元模拟,如图1所示。采用修正的 Davidenkov 黏弹性动力本构模型模拟土的动力特性;地铁盾构隧道模型采用弹性模型,结构采用C30混凝土[10-11],其弹性模量为30 GPa,泊松比0.25,重度25 kN/m3,纵向刚度等效比取0.65[12]。

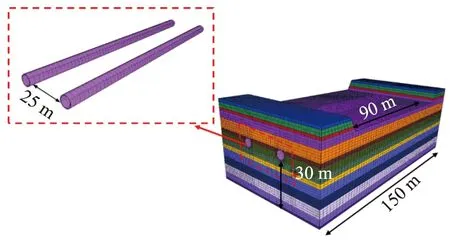
图1 盾构隧道三维数值分析模型Fig. 1 Three-dimensional numerical analysis model of shield tunnel

计算中使用了FLAC3D中的局部阻尼,其通过在振动循环中在节点上增加或者减小质量,由于增加的质量和减小的质量相同,因此整个系统质量守恒。

当节点速度符号改变时,质量增加,当速度达到最大值或者最小值时,质量减少。因此损失的能量ΔW是最大瞬时应变能W的一定比例(ΔW/W),此比例是率无关和加载频率无关的。ΔW/W是临界阻尼比D的函数:

aL=πD

式中:αL为局部阻尼系数,D为临界阻尼比,本文中阻尼比选取为5%,因此局部阻尼系数设置为0.1571(=0.05π)。

本文采用了模型底部固定,四周分别约束对应水平位移,上表面完全自由的边界条件;在动力分析计算中采用了底部黏性边界,模型四周设置为自由场边界,既防止了边界上波的反射,达到与无限场地相同的效果。通过土弹簧方式将土体的变形作用于隧道和竖井,以模拟土-结构相互作用[8]。

1.2 模型验证

为验证数值计算模型的适用性,采用时程分析方法,在FLAC3D中将模型底部视为基岩,将目标地震动(Kobe波)施加在基岩上,地震动经过传播施加到目标结构上。将结果与WANG[13]提出的评价隧道在地震作用下的最大弯矩的理论公式进行对比。

数值计算采用修正的Davidenkov黏弹性动力本构模型模拟土的动力特性,区间隧道结构弹性模量为3.45×104MPa,泊松比为0.18,轴心抗压强度35.5 MPa,轴心抗拉强度2.64 MPa,采用横向等效刚度比按照0.75进行计算。选取天津某软弱地基土层进行计算,厚度3 m,重度20 kN/m3,弹性模量12.28 MPa,泊松比0.44,黏聚力15.1 kPa。取自由场对应隧道埋深位置处最大剪应变带入理论公式计算分析。如图2所示,两者吻合的较好,证明了所建立数值模型的正确性与可靠性。

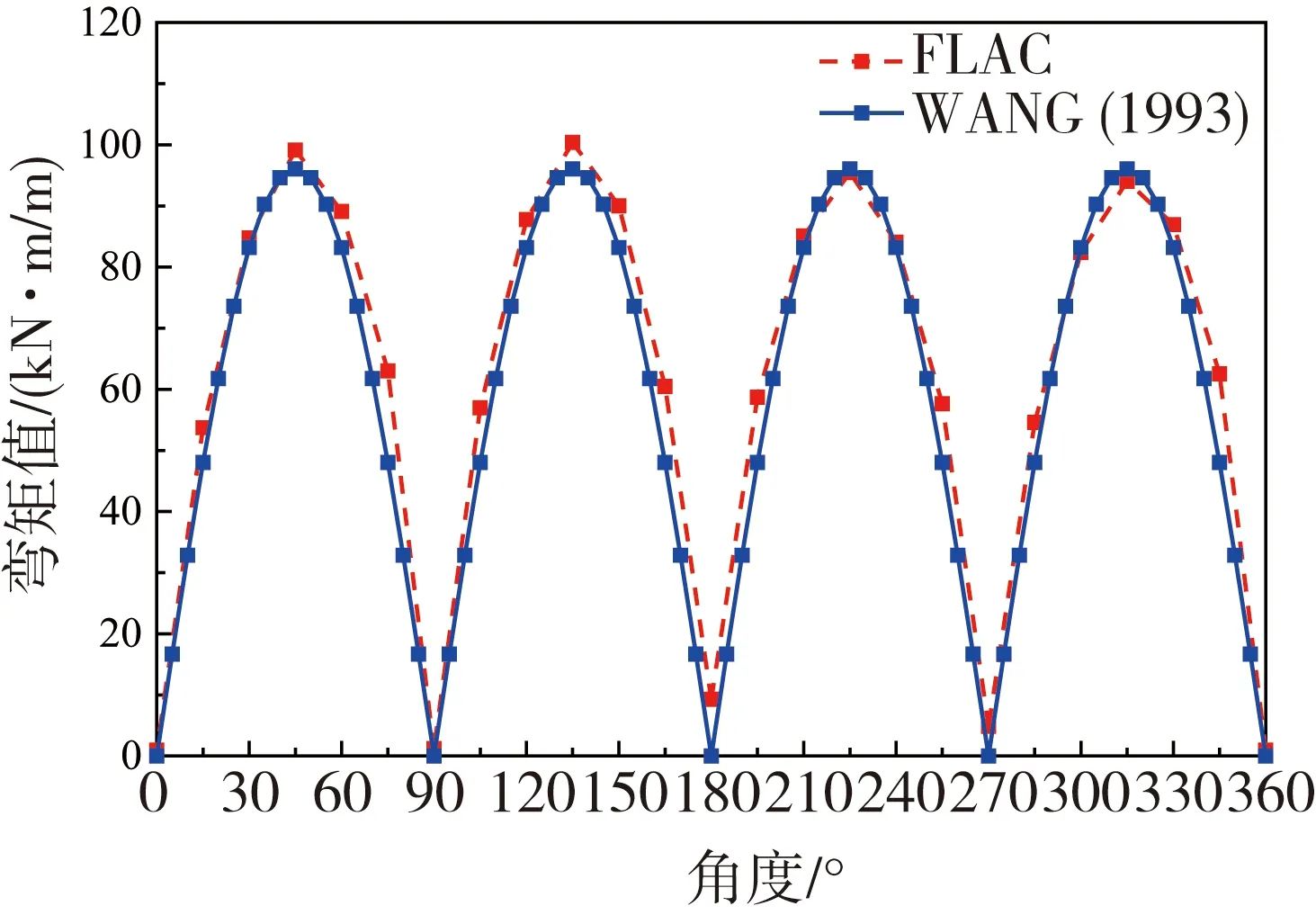
图2 数值结果与理论公式对比Fig. 2 Numerical results compared with theoretical formula

2 盾构隧道下穿河流段地震反应特性

2.1 下穿段盾构隧道在地震作用下应力反应规律

根据天津市该段隧道地震安全评测结果,基岩峰值加速度近似可取0.15、0.20和0.30 g,其中: g为重力加速度,分别对应小震、中震与大震。数值模型中采用时程分析方法,将模型底部视为基岩,将目标地震动(Kobe波,El-Centro波)施加在基岩上,地震动经过传播施加到隧道结构。本文中选取河道中心底部(S=75 m)以及河岸底部(S=25 m)的A隧道截面进行分析,如图3所示。

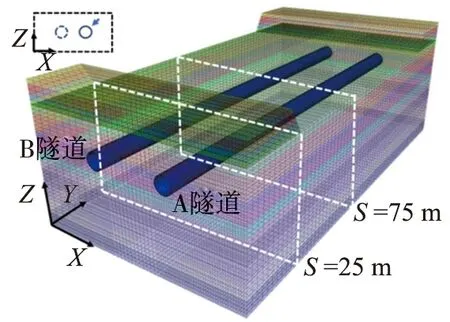
图3 选取的典型隧道截面位置示意图Fig. 3 Selected schematic diagram of typical tunnel section position

计算结果显示,隧道的最大主应力出现在河岸底部隧道环上(S=25 m),其截面最大主应力分布如图4所示,图中最大拉应力出现在左拱肩的位置,而最大压应力分布在右拱肩以及左拱腰部,分析结果表明盾构隧道的拱肩以及拱腰是地震作用下应力分布较大的位置。

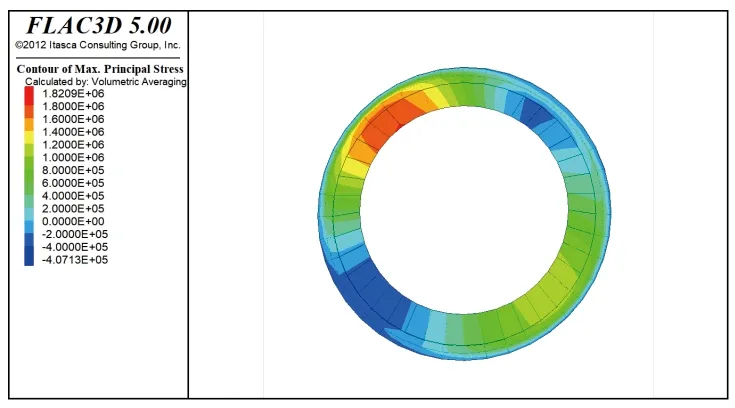
图4 隧道地震中典型最大主应力分布 (S=25 m)Fig. 4 Typical maximum principal stress distribution in tunnel (S=25 m)

通过分析盾构隧道在不同地震动下的最大最小主应力包络图,如图5所示。在El-Centro波作用下,河岸底部隧道截面(S=25 m)处出现了大拉应力,其中在基岩输入地震动为0.15、0.20和0.30 g时,最大拉应力分别为0.8、1.75和3.3 MPa,在此时混凝土有开裂的风险,而在河道底部 (S=75 m) 处则没有出现拉应力,0.30 g地震动作用下最大压应力为0.5 MPa,盾构隧道此时处于安全状态。在Kobe波作用下,河岸底部隧道截面出现了大拉应力,最大拉应力分别为0.5 MPa和0.6 MPa,隧道处于安全状态。在天津某下穿海河段工程地质条件下,盾构隧道的内力反应对El-Centro波较为敏感,在这种主频范围的地震动作用下,河岸底部盾构隧道截面有开裂的危险。

2.2 下穿段盾构隧道在地震作用下相对水平位移反应规律

对于沿海城市的软土地层,在强震动作用下会发生较大的变形,土的变形通过土-结构物相互作用效应,导致盾构隧道产生相应变形,结构可能由于局部变形过大而发生损伤,甚至会发生塑性变形而破坏[13-14]。将地震动作用下地铁区间隧道不同高度处的相对水平位移时程与隧道底部的相对水平位移时程之差定义为隧道相对侧向位移[15]。图6是地震作用中的盾构隧道的典型位移云图,从图中可以看出:河道下方隧道由于上部地应力相对河岸较小,导致河道下方隧道变形较大。

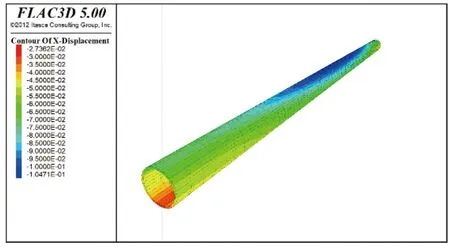
图6 地震中盾构隧道典型位移分布Fig. 6 Typical displacement distribution of shield tunnel in earthquake

周围土体变形是直接影响地下结构反应的主要因素,本文以基岩输入El-Centro波为例,探究下穿海河盾构隧道不同位置处(河道下,河岸下)的相对侧移反应,以及相同深度隧道附近土体和自由场土体位移反应。当区间隧道顶部与底部对应的土层深度处在相对位移绝对值最大时,分别给出了对应于隧道高度的自由场侧向土层水平相对位移反应值随隧道高度的变化曲线,如图7-8所示。

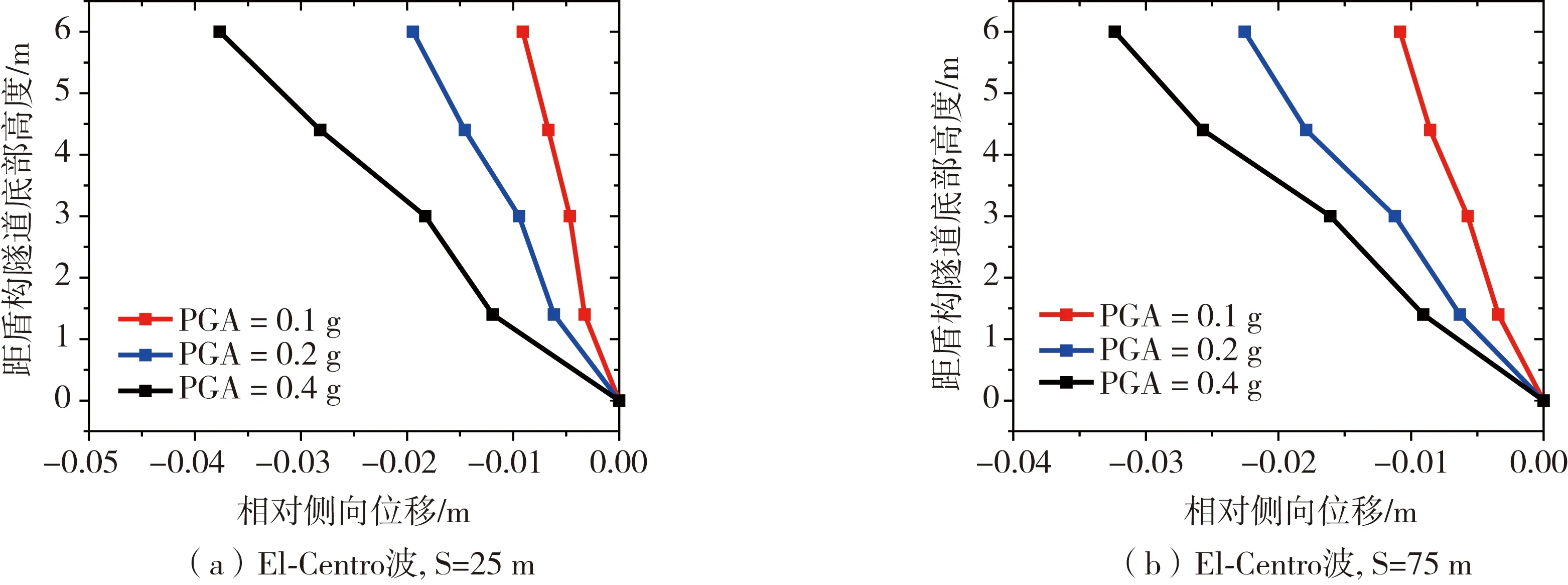
图7 El-Centro波作用下隧道产生的最大相对侧向位移Fig. 7 Maximum relative lateral displacement of tunnel under El-Centro wave

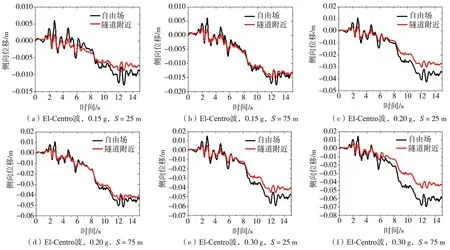
图8 El-Centro波作用下隧道附近土体与自由场位移时程对比Fig. 8 Time-history comparison of displacement of soil near the tunnel and that in the free field under the action of El-Centro wave

由隧道在地震过程中产生的最大相对侧移分布可以看出:随着基底输入加速度的增大,隧道及土体位移,以及隧道顶底的相对侧移增大。基岩输入El-Centro波时,隧道顶底最大侧移发生在12～13 s范围内;对于El-Centro波这类中低频成分较多的地震动,隧道相对侧移反应随着距隧道底部距离增大而增大,隧道相对侧向位移最大值出现在拱顶位置。河道下方的隧道相对侧移反应与河岸下方相差不大,相对侧移反应在1.5～2.5 cm之间;对不同烈度地震作用下,截面变形进行验算可以发现,在7度地震作用下,河道中间和坡脚下方隧道最大直径变形率分别为1.22‰和0.95‰,小于我国地铁设计规范限值4‰～6‰[16],满足规范要求;在8度地震作用下,河道中间隧道最大直径变形率为5.38‰,小于规范限值6‰,满足规范要求;而坡脚下方隧道最大直径变形率为6.45‰,大于规范限值,需要适当提高隧道构件强度[17]。