大跨度弦支穹顶结构多维多点随机地震响应分析

吕迎新,王 宇

(沈阳建筑大学 土木工程学院,辽宁 沈阳 110168)

0 引言

弦支穹顶结构是一种新型刚柔结合的空间结构体系,由上部单层网壳与下部索杆体系组成。由于预应力拉索的布置提高了结构的刚度与整体稳定性,弦支穹顶结构拥有较强的跨越能力,广泛应用于体育馆和展览馆等大跨度公共建筑。有关弦支穹顶结构抗震性能的研究,文献[1]考虑结构静力初始状态,对一大跨度椭球形弦支穹顶结构进行了模态分析;并采用时程分析法对其进行了地震响应分析,得到了弦支穹顶结构具有较高的整体刚度,考虑杆件的初始弯曲对结构响应的影响较小的结论。文献[2]以某弦支穹顶屋盖为研究对象,对结构进行了考虑行波效应的地震时程响应分析,研究结果表明:当相位差较大时,结构的内力与位移均相较一致输入有显著的增大。

文献研究表明:地震动多点激励对大跨度建筑结构有着不可忽视的影响,是抗震研究的重要内容之一,造成地震动空间变化的原因主要有行波效应、部分相干效应与场地效应。对结构进行多点输入响应分析方法主要有时程分析法、多点反应谱法与随机振动法,其中时程分析法应用最为成熟广泛,但其所得到的结果极其依赖于所采用地震动时程的特性;多点输入反应谱法由于计算量较大,无法保持传统反应谱法简化计算的特点,因此基于地震动概率统计特性的随机振动法被视为最为合理的方法。由林家浩等[3]提出的虚拟激励法,在保证足够计算精度的前提下,极大的降低了计算量;目前已有很多学者基于该方法进行了各类大跨度空间结构多点激励影响效应分析[4-6]。

基于以上研究背景,本文以一大跨度弦支穹顶结构—济南奥体中心体育馆为研究对象,考虑结构静力初始状态,采用虚拟激励算法,分析了行波效应、部分相干效应和二者耦合效应以及考虑多维地震输入对结构随机地震响应的影响,旨在为该类结构抗震设计提供一定参考。

1 结构多点输入下随机地震反应的虚拟激励法

地震动多点激励的运动方程为:

(1)

式中:M、C和K分别为质量矩阵、阻尼矩阵和刚度矩阵,下标ss、bb、sb和bs分别代表非支座节点自由度和支座节点自由度及二者间的耦合,Xb表示地震作用下支座处的地面强迫位移向量,Xs表示结构非约束自由度的绝对位移向量,Pb为支座所受的反力向量。

为求解式(1),将式中绝对位移项Xs分解为拟静力位移Ys和动态位移Yr之和,即:

(2)

同时考虑行波效应、部分相干效应与场地效应,n个支座处地震动加速度功率谱矩阵可以表示为:

S(ω)≡[B]*[J][R][J][B]

(3)

式中:

B=diag[exp(-iωT1),exp(-iωT2),…exp(-iωTn)]

(4)

(5)

(6)

式中:Sii(ω)(i=1,2,…,n)为各点的自功率谱密度,B为行波效应矩阵,J为相干矩阵;Ti为第i个支座节点相对坐标原点的运动时间差。

由于R为一非负定实对称矩阵,对其进行复特征值分解为m个非零实特征值aj及实特征值向量{φj},(m=rank(R))构造m个虚拟简谐加速度:

何牦将信纸举过头顶，摆动干树枝般的手臂，信纸如一面小红旗在舞动。橘红回信了，橘红回信了！何牦的声音仿佛在整条竹溪街回响。曾有邻居劝他，这是大海捞针，死了心吧，用这份心思找个女人好好过日子。他想幸亏没接受别人的好意，这不橘红回信了？

(7)

将式(7)与式(2)代入式(1),并假定采用集中质量矩阵且阻尼项与相对速度成正比可得结构的位移稳态响应为:

(8)

式中:H(ω)为频响函数矩阵,Φ为模态矩阵,式F=-[Kss]-1[Ksb]为影响矩阵,其力学意义为由支座节点发生单位位移所引起结构非支座节点的拟静力位移。

因此,结构的位移功率谱可以表达为:

(9)

根据结构虚拟位移响应通过有限元方法得到任意单元节点的虚拟内力,然后可求得对应的内力功率谱密度,根据功率谱密度可求得响应的各阶谱矩,进而根据随机振动理论计算响应的极值期望值[7-8]。

2 工程背景及有限元模型

表1 索杆结构截面规格Table 1 Section specification of cables and poles

图1 弦支穹顶结构平面图与剖面图 图2 索杆部分示意图Fig. 1 Structural sketch of suspen-dome structure Fig. 2 Diagram of cables and poles

利用通用有限元软件ANSYS建立结构模型,上部网壳杆件采用Beam188单元模拟,拉索采用设置只拉选项的Link10单元模拟,竖向撑杆采用Link8单元模拟,附加恒载采用Mass21单元模拟;假定上部网壳各杆件为刚接,拉索、撑杆与网壳间为铰接,结构周边节点为铰接,施加三向位移约束;阻尼采用Rayleigh阻尼模拟,阻尼比取0.02;环索的预应力通过设置单元初始应变模拟。

大跨度弦支穹顶结构具有较强的几何非线性,为考虑几何刚度效应的影响,应先进行结构在自重、恒载作用以及预应力共同作用下的非线性静力分析以获取结构的初始平衡态,存储刚度矩阵,在此基础上进行结构振动模态计算以及虚拟激励求解的复谐响应分析与静力分析。

根据以上总体思路,基于ANSYS平台的分析流程主要包括:结构建模及获取初始平衡态、结构质量矩阵与刚度矩阵提取及合成多点虚拟激励、进行各频率点包括Harmonic分析与Static分析的虚拟激励求解、对虚拟响应量进行后处理以计算结构响应的功率谱矩阵及相关量。

三维有限元模型建立后,利用子空间迭代法对结构进行自振模态计算,如图3所示,结构前40阶自振频率分布在1.63 Hz至2.6 Hz之间,各阶频率变化不大,可见该大跨度弦支穹顶结构自振频率分布密集特征极为显著。

图3 自振频率分布Fig. 3 Distribution of natural frequencies

3 随机地震响应

3.1 功率谱模型

(10)

式中:ω为角频率,S0为谱强度因子,ωg与ζg为覆盖土层卓越频率与阻尼比,ωf与ζf为与滤波特性相关的参数。

该工程按设防烈度8度,Ⅲ类场地,设计地震分组为第一组进行分析,参数S0、ωg、ωf、ζg、ζf为参考文献[6]建议进行取值,考虑地震动多维输入,水平X向、水平Y向与竖向的谱强度因子S0按1:0.85:0.65进行调整,各激励分量间相关性按地震主轴理论处理[10],积分区间为[0,200]rad/s,步长取0.1 rad/s。

3.2 行波效应

本节主要研究行波效应的影响,假定地震动传播方向如图4所示,结构支座最大间距为122 m,最小间距为0.93 m,地震波视波速实际是与频率有关的函数,但由于影响因素很多,在确定分析中的视波速时通常将其取为常数[11-12]。本文选取两种视波速分别为1000 m/s、2000 m/s以及视波速为无穷即一致激励,分别获各个激励点处的相位差,采用虚拟激励法,对上述三种情况下的动力响应进行了计算。由于弦支穹顶结构构件以承受轴向力为主,因此本文主要分析轴向地震内力响应情况,图5-6给出了结构第594号和339号单元在不同视波速下的轴力功率谱密度曲线对比,可见考虑行波效应,构件随机响应的功率谱密度在波峰处出现明显增大,且提升程度随着视波速的减小而增大,其中594号单元功率谱在低频范围内提升较大,由于拟静力响应具有主要影响结构低频响应的特点,因此该构件受拟静力影响程度较大。

图4 地震传播方向Fig. 4 Direction of earthquake propagation

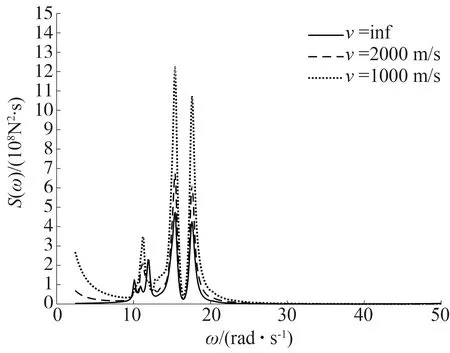
图5 594号单元轴力功率谱密度Fig. 5 Power spectral density of axial force in element 594

图6 339号单元轴力功率谱密度Fig. 6 Power spectral density of axial force in element 339

图7给出了在不同视波速作用下,各环径向杆、环向杆、拉索与竖向撑杆的轴力响应情况,所选单元编号如图2所示,本文轴力响应指的是在随机地震作用下轴力极值的数学期望。可见对于弦支穹顶上部网壳结构,在地震作用下,网壳径向杆件内力在靠近结构跨中位置处最大,向外环逐渐减小,在距离支座四分之一跨度处至支座位置逐渐增加;环向杆内力在第2环、第6环与第7环较大,除边缘特殊杆件,环向杆地震内力一般大于径向杆;同时可见相较普通单层网壳结构,弦支穹顶结构各环地震内力响应分布比较均匀,这是由于下部拉索的布置使结构受力更为合理。所选径向杆在波速为2000 m/s和1000 m/s时最大轴力响应分别为277.09 kN和366.31 kN,分别相较相应杆件一致输入时增大了23%和62%;环向杆在波速为2000 m/s和1000 m/s时最大轴力响应分别为330.57 kN和419.63 kN,分别相较相应杆件一致输入时增大了16%和47%;竖向撑杆在波速为2000 m/s和1000 m/s时最大轴力响应分别为6.39 kN和8.57 kN,分别相较相应杆件一致输入时增大了19%和59%。同时可见最外环环向杆在一致输入下引起的内力接近于0,但在行波输入下,其内力由于支座非一致运动所产生的拟静力响应直接作用而远大于一致输入下的地震内力。环索地震内力从内之外依次增大,一致输入下分别为77.25 kN、167.42 kN和216.89 kN,但考虑两种视波速其内力相比一致激励基本持平。

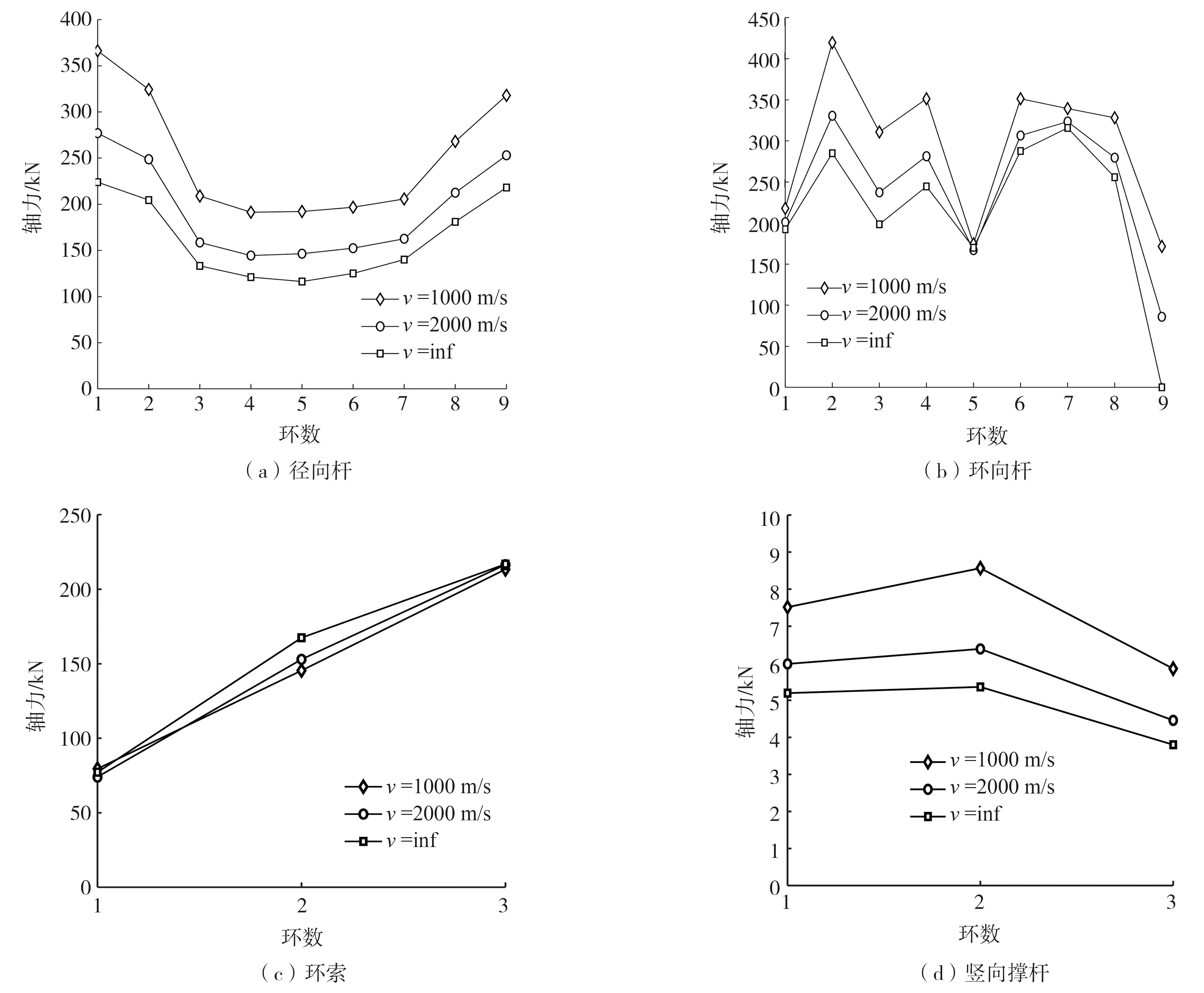
图7 不同视波速下构件轴力响应Fig. 7 Axial force of members due to different wave velocities

图8给出了两种不同视波速下上部网壳结构与下部索杆体系的俯视轴力云图。从以上结果可以看出:大跨度弦支穹顶结构受行波效应影响显著,结构重要构件内力出现明显提升且提升的程度随着视波速的减小而增大;同时可见:由于弦支穹顶结构具有对称性,在一致激励下,其内力分布也是对称的,但考虑行波效应后结构内力响应分布不再对称,产生这种情况的原因是在非一致输入下由于地震荷载空间分布的变化激起结构中反对称振型的振动。

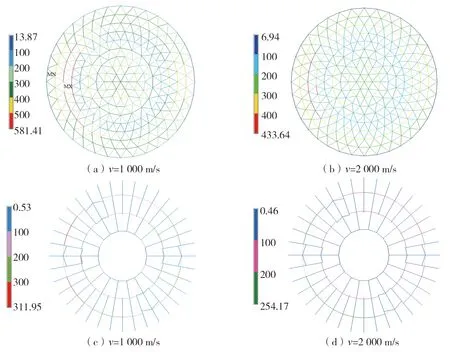
图8 不同视波速下结构轴力响应云图(kN)Fig. 8 Contour of axial force response of the structure due to different wave velocities(kN)

3.3 多点随机激励

地震波在传播过程中经过多次反射、折射及散射,会引起各激励点处的频散损失即部分相干效应,本节将研究部分相干效应、同时考虑行波效应与部分相干效应以及考虑地震动单维输入与多维输入对大跨度弦支穹顶随机地震响应的影响。目前的研究中相干函数经验模型一般以台阵记录的地震通过相干性分析得到,本文相干函数模型采用屈铁军-王君杰模型[13]:

|γ(ω,d)|=e-a(ω)db(ω)

(11)

式中:a(ω)=a1ω2+a2,b(ω)=b1ω+b2,d为两点间沿地震波传播方向的水平距离,参数:a1=0.00001678,a2=0.001219,b1=-0.0055,b2=0.7674。

为了使研究结果更好的对比,共选取五种工况进行对比分析:工况1为一致输入即相干性为完全相干和视波速为无穷;工况2为仅考虑部分相干效应;工况3为仅考虑行波效应输入(视波速2000 m/s);工况4为同时考虑行波效应与部分相干效应(视波速2000 m/s);工况5为多点输入下仅考虑单维(水平X向)地震激励,为将非一致输入与一致输入下计算所得结果进行比较,定义影响系数γ如下:

(12)

结构在不同工况作用下各类型地震内力最大杆件即控制杆件响应值及γ>1.2单元所占比例见表2,图9给出了工况2与工况4下上部网壳结构与下部索杆体系轴力俯视云图。

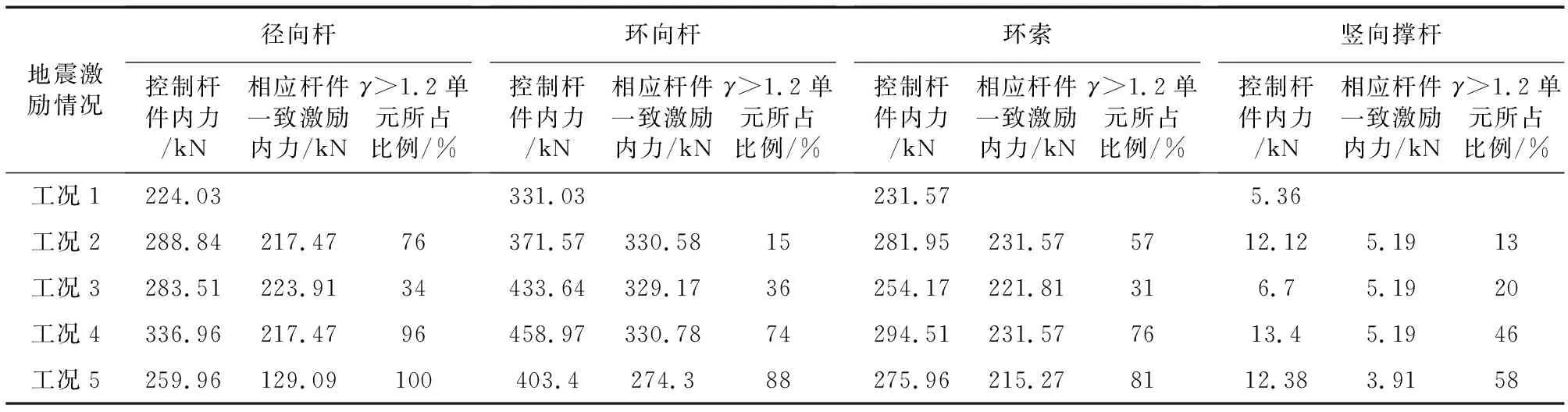
表2 不同工况下杆件统计分析表Table 2 Statistical table of rods under different seismic excitations

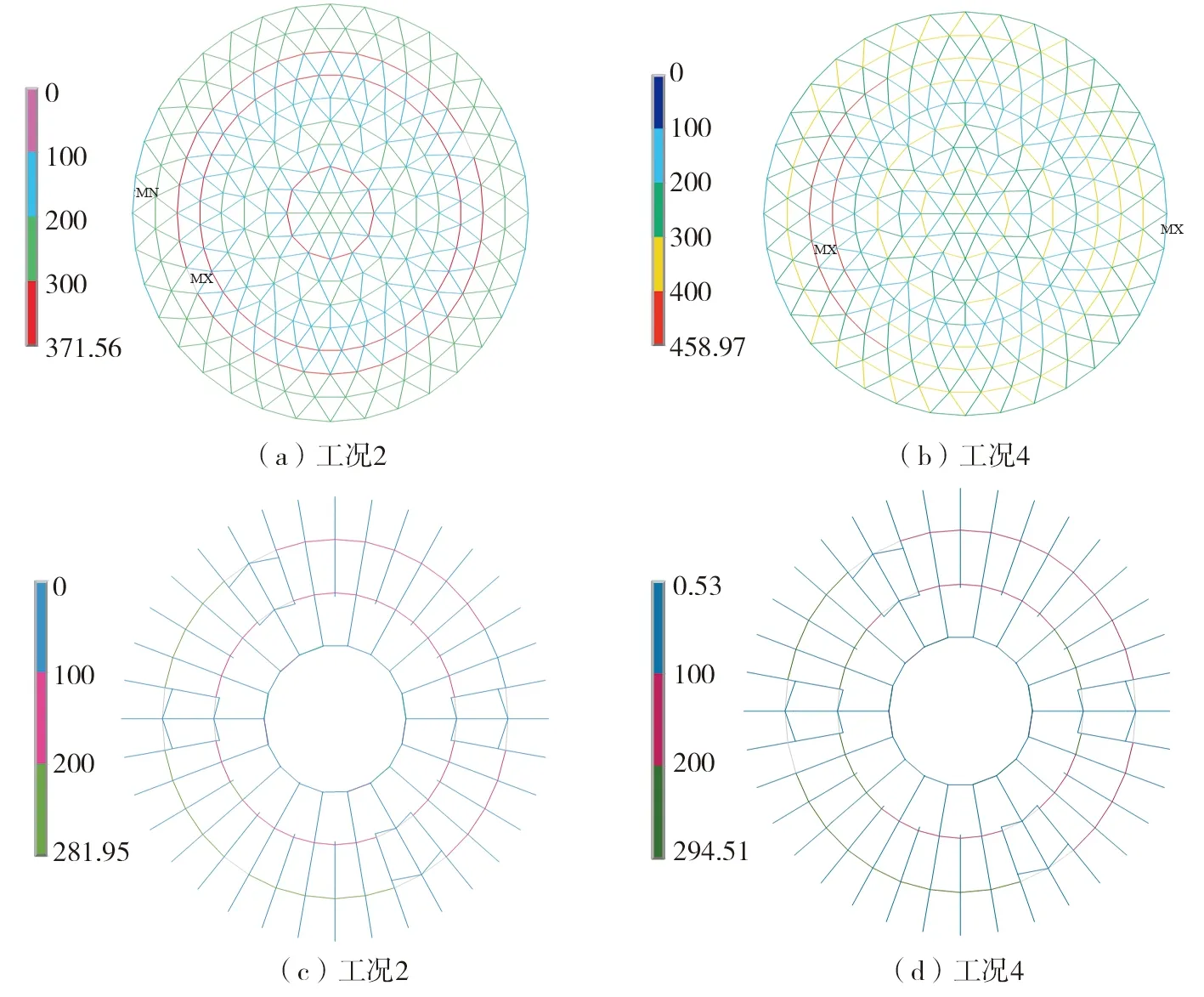
图9 不同工况下结构轴力响应云图(kN)Fig. 9 Contour of axial force response of the structure due to differentseismic excitations(kN)

仅考虑部分相干效应时,径向杆、环向杆、环索与竖向撑杆控制杆件地震内力增幅分别达到了29%、12%、22%及126%,可见考虑部分相干效应对结构地震响应影响显著,在视波速2000 m/s时,对于下部索杆体系,相干效应相比于行波效应对其内力放大作用更为明显。由于行波效应和部分相干效应均对弦支穹顶结构产生不利影响,各类构件控制杆件内力以及γ>1.2所占比例大多在工况4下出现最大值,即同时考虑行波效应和部分相干效应最为不利,径向杆、环向杆、环索与竖向撑杆控制杆件地震内力增幅分别达到了50%、39%、27%与150%,相比一致输入提升幅度大于20%的杆件占比达到96%、74%、76%与46%,因此为了对大跨度弦支穹顶结构进行合理的抗震分析,应当根据场地条件选取多种可能的地震波视波速,同时考虑部分相干效应进行计算,否则会低估结构的地震响应,以至造成设计错误;多点输入下上部网壳增大最为明显的构件主要集中在支座附近及1/4跨度处,径向杆的提升程度相比环向杆更为明显,下部索杆体系增大最为明显的构件主要位于最外环,设计时应注意多点输入对这部分杆件内力的影响,可采取适当增大这部分杆件截面以确保安全。对比工况4与工况5的结果可见:考虑地震动多维输入结构控制杆件内力相比仅考虑单维输入增幅达到了30%,对该类结构进行抗震分析应充分考虑地震动的多维性。考虑多维多点输入下各类构件最大应力均小于抗拉强度标准值,满足设计要求。

4 结论

本文基于虚拟激励法,以一大跨度弦支穹顶结构—济南奥体中心体育馆为工程背景,分析了行波效应、部分相干效应和二者耦合效应以及考虑多维地震输入对结构随机地震响应的影响,研究结果表明:

1) 大跨度弦支穹顶结构受行波效应影响显著,考虑行波效应后,重要构件内力响应出现较大幅度提升,提升的程度随着视波速的降低而增大,因此准确的评估视波速尤为重要;且考虑行波效应由于地震荷载空间分布的变化,结构内力分布与一致激励出现明显区别。

2) 考虑部分相干效应明显增大了结构内力响应,径向杆、环向杆、环索与竖向撑杆控制杆件内力相较一致激励分别增大29%、12%、22%及126%,部分相干效应对下部索杆结构内力影响相较行波效应更为明显。

3) 多点输入下,径向杆、环向杆、环索与竖向撑杆控制杆件地震内力增幅分别达到了50%、39%、27%及150%,单独考虑行波效应或部分相干效应不能得到结构的最不利响应;考虑地震动空间变化效应后,弦支穹顶结构不同类型,不同位置构件内力的变化程度存在较大差异,需对具体响应具体分析,其中上部网壳增大最为明显的构件主要集中在支座附近及1/4跨度处,径向杆的提升程度相比环向杆更为明显,下部索杆体系增大最为明显的构件主要位于最外环,设计时应注意多点输入对这部分杆件内力的影响;考虑地震动多维输入内力增幅达到30%。

本文对一大跨度弦支穹顶结构进行的多维多点地震响应分析对该类结构的抗震设计具有一定参考意义,但地震多点激励分析具有一定特殊性,在实际抗震设计中定量结果还需针对具体结构进行分析。