连梁刚度折减系数对剪力墙结构的影响研究
2023-11-01杨志勇乔保娟肖从真李志山
贾 苏,杨志勇,乔保娟,肖从真,李志山
(1. 中国建筑科学研究院有限公司, 北京 100013; 2. 广州建研数力建筑科技有限公司, 广州 510170)
0 引言
剪力墙结构是一种采用钢筋混凝土墙板承受竖向和水平力的结构体系,在高层和超高层房屋中被大量运用[1]。由于建筑使用功能和结构受力要求,在剪力墙上设置洞口会形成联系两片墙肢的连梁。连梁作为耗能构件,对剪力墙结构的内力和变形有很大的影响[2]。
在地震作用下,由于连梁受力集中,容易开裂,导致地震力降低。为了考虑连梁这种受力特点,《建筑抗震设计规范》(GB 50011—2010)[3]第6.2.13-2条规定,抗震墙地震内力计算时,连梁的刚度可折减,但折减系数不宜小于0.50。在剪力墙结构设计中,根据结构特点,一般取0.6~0.7的连梁刚度折减系数进行全楼统一计算[3-4]。但实际结构中不同部位连梁的内力和变形不同,实际所产生的刚度退化也差别很大,统一的连梁刚度折减系数会导致结构内力和变形计算存在一定误差。
文献[5-6]通过对连梁试验结果进行分析,给出连梁在往复荷载作用下的标准骨架曲线。文献[7]考虑连梁在小震和中震下的刚度退化情况,提出了一种基于非线性分析的较为准确地确定连梁刚度折减系数的计算方法。
在数值仿真中,连梁构件可采用平面应力条件下的混凝土弹塑性损伤模型进行模拟,可较为真实的反映连梁构件混凝土残余变形、拉压异性和静水压力等力学特性[8-9]。通过建立整体结构的弹塑性分析模型,进行弹塑性时程分析可得到连梁在不同设防烈度烈度下的刚度折减系数[10]。文献[11]采用弹塑性分析确定连梁刚度折减系数并在实际工程中获得了应用。
本文对9栋典型高层剪力墙结构进行非线性分析,确定其连梁刚度折减系数,并采用反应谱方法对连梁刚度弹塑性算法和常规全楼统一折减算法进行了对比,研究了两种连梁刚度折减计算方法对剪力墙结构响应的影响。
1 模型简介
9栋典型剪力墙结构抗震设防烈度分别为6度~8度(0.30 g),其中高烈度区8度(0.20 g)和8度(0.30 g)5栋,低烈度区(6度和7度)4栋,剪力墙平面形式包括工字形平面、矩形平面、多边形平面和T型平面等,各结构基本信息及结构布置见表1。
1.1 整体指标
设定不同全楼连梁刚度折减系数后,结构主要指标对比见表2-表4。
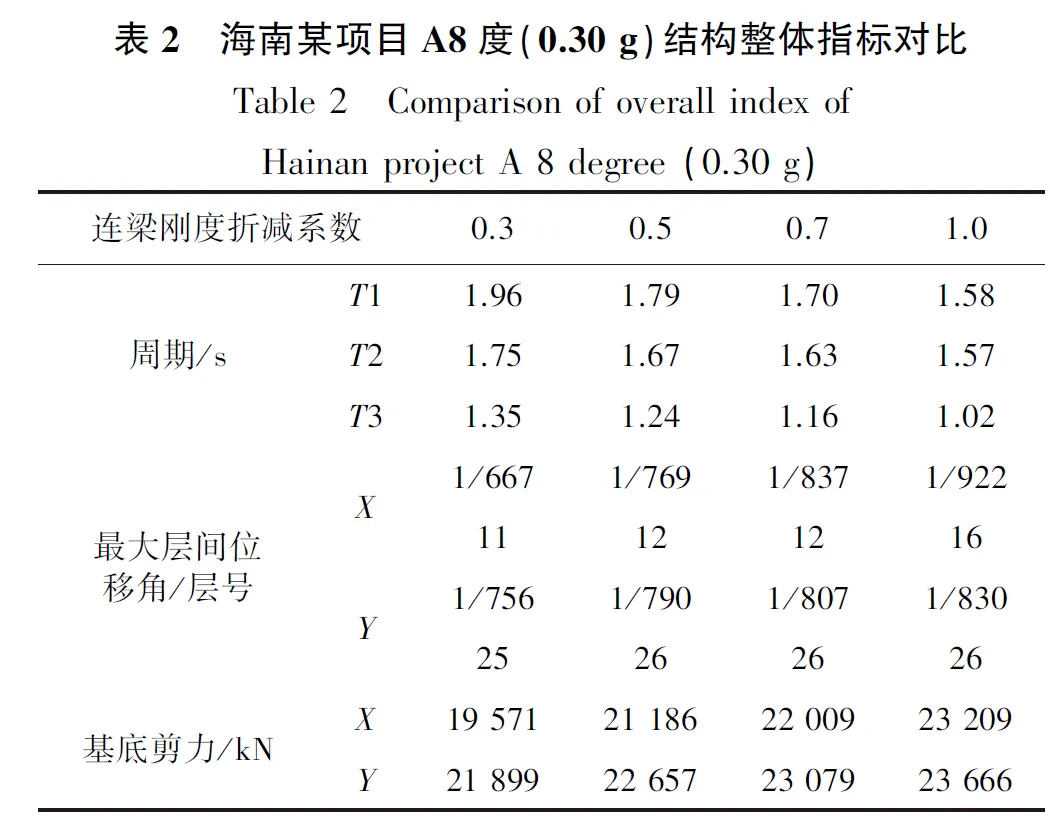
表2 海南某项目A8度(0.30 g)结构整体指标对比Table 2 Comparison of overall index of Hainan project A 8 degree (0.30 g) 连梁刚度折减系数0.30.50.71.0周期/sT11.961.791.701.58T21.751.671.631.57T31.351.241.161.02最大层间位移角/层号X1/6671/7691/8371/92211121216Y1/7561/7901/8071/83025262626基底剪力/kNX19 57121 18622 00923 209Y21 89922 65723 07923 666
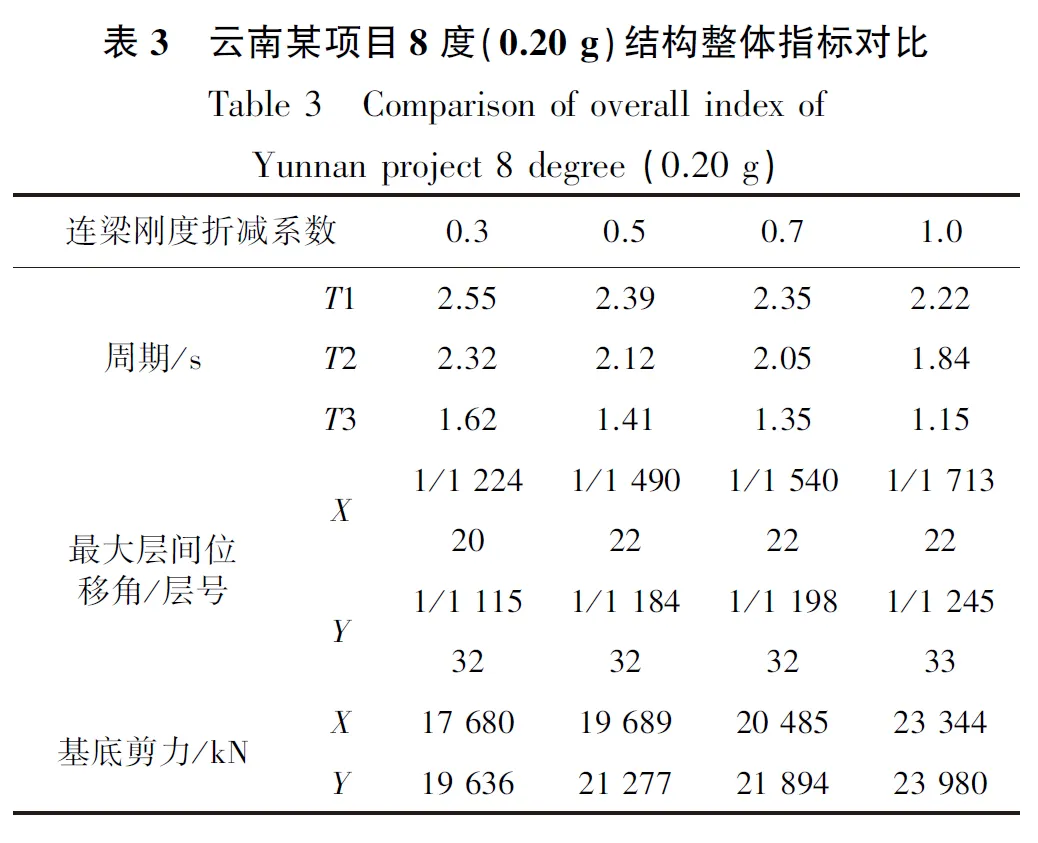
表3 云南某项目8度(0.20 g)结构整体指标对比Table 3 Comparison of overall index of Yunnan project 8 degree (0.20 g)连梁刚度折减系数0.30.50.71.0周期/sT12.552.392.352.22T22.322.122.051.84T31.621.411.351.15最大层间位移角/层号X1/1 2241/1 4901/1 5401/1 71320222222Y1/1 1151/1 1841/1 1981/1 24532323233基底剪力/kNX17 68019 68920 48523 344Y19 63621 27721 89423 980
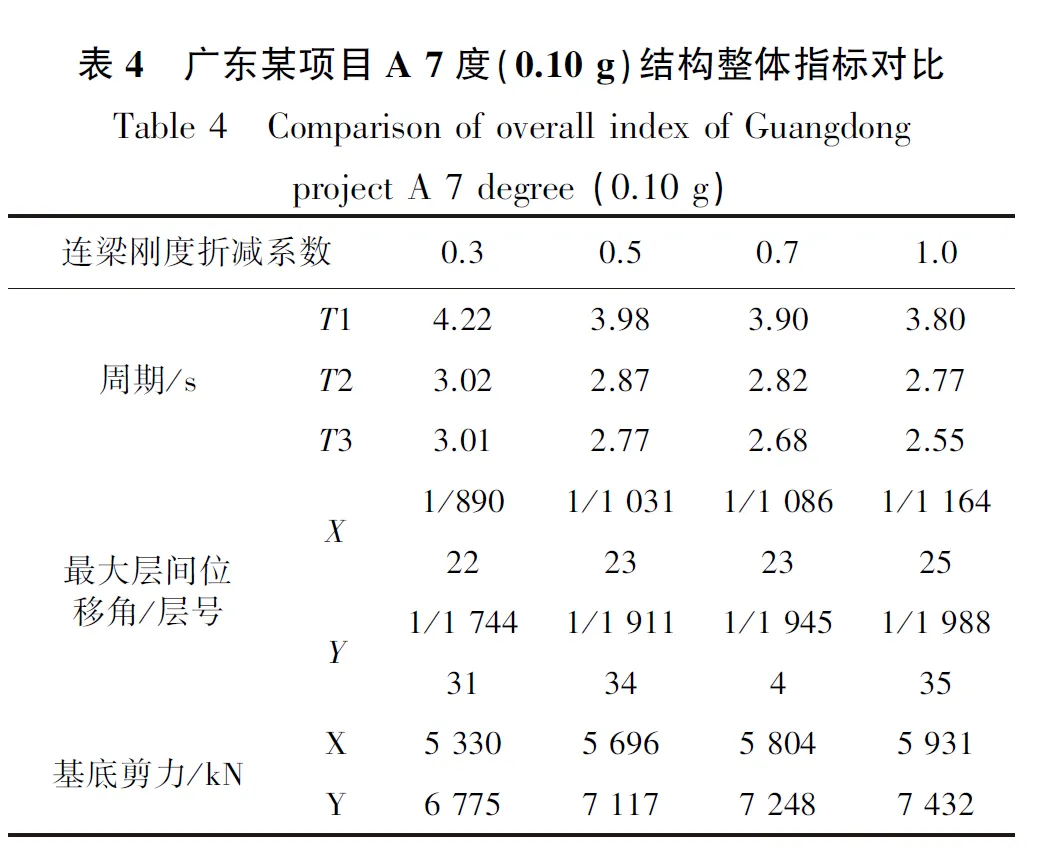
表4 广东某项目A 7度(0.10 g)结构整体指标对比Table 4 Comparison of overall index of Guangdong project A 7 degree (0.10 g)连梁刚度折减系数0.30.50.71.0周期/sT14.223.983.903.80T23.022.872.822.77T33.012.772.682.55最大层间位移角/层号X1/8901/1 0311/1 0861/1 16422232325Y1/1 7441/1 9111/1 9451/1 9883134435基底剪力/kNX5 3305 6965 8045 931Y6 7757 1177 2487 432
为便于对比,本文以连梁刚度折减系数0.7为基准,与规范下限0.5连梁刚度折减系数模型和上限1.0连梁刚度折减系数模型分别进行比较,结果见表5。可以看出:结构整体指标存在1.2%~14.8%的差别。
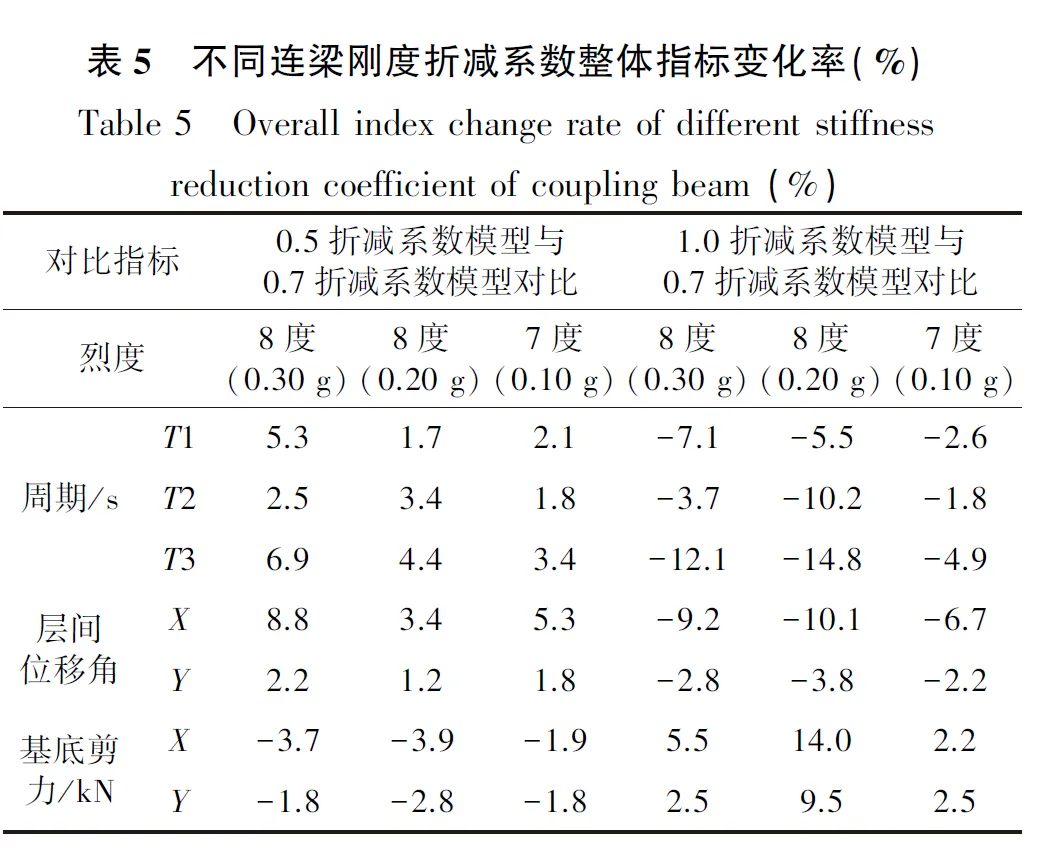
表5 不同连梁刚度折减系数整体指标变化率(%)Table 5 Overall index change rate of different stiffness reduction coefficient of coupling beam (%)对比指标0.5折减系数模型与0.7折减系数模型对比1.0折减系数模型与0.7折减系数模型对比烈度8度(0.30 g)8度(0.20 g)7度(0.10 g)8度(0.30 g)8度(0.20 g)7度(0.10 g)周期/sT15.31.72.1-7.1-5.5-2.6T22.53.41.8-3.7-10.2-1.8T36.94.43.4-12.1-14.8-4.9层间位移角X8.83.45.3-9.2-10.1-6.7Y2.21.21.8-2.8-3.8-2.2基底剪力/kNX-3.7-3.9-1.95.514.02.2Y-1.8-2.8-1.82.59.52.5
1.2 构件内力
以海南某项目A作为研究对象,选取两片典型剪力墙进行内力对比分析,结构标准层平面图与剪力墙位置如图1所示。
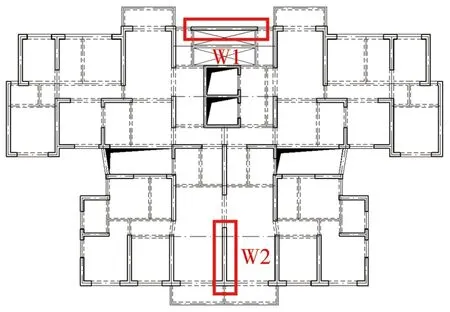
图1 模型标准层平面布置图Fig. 1 Layout plan of model standard floor
对于不同连梁刚度折减系数模型,W1和W2墙肢在地震工况下构件内力变化如图2-3所示。结果表明:剪力墙在连梁刚度折减系数分别取0.5和1.0下,剪力存在-4%~33%的差异,弯矩存在-36%~15%的差异,轴力存在-41%~13%的差异。
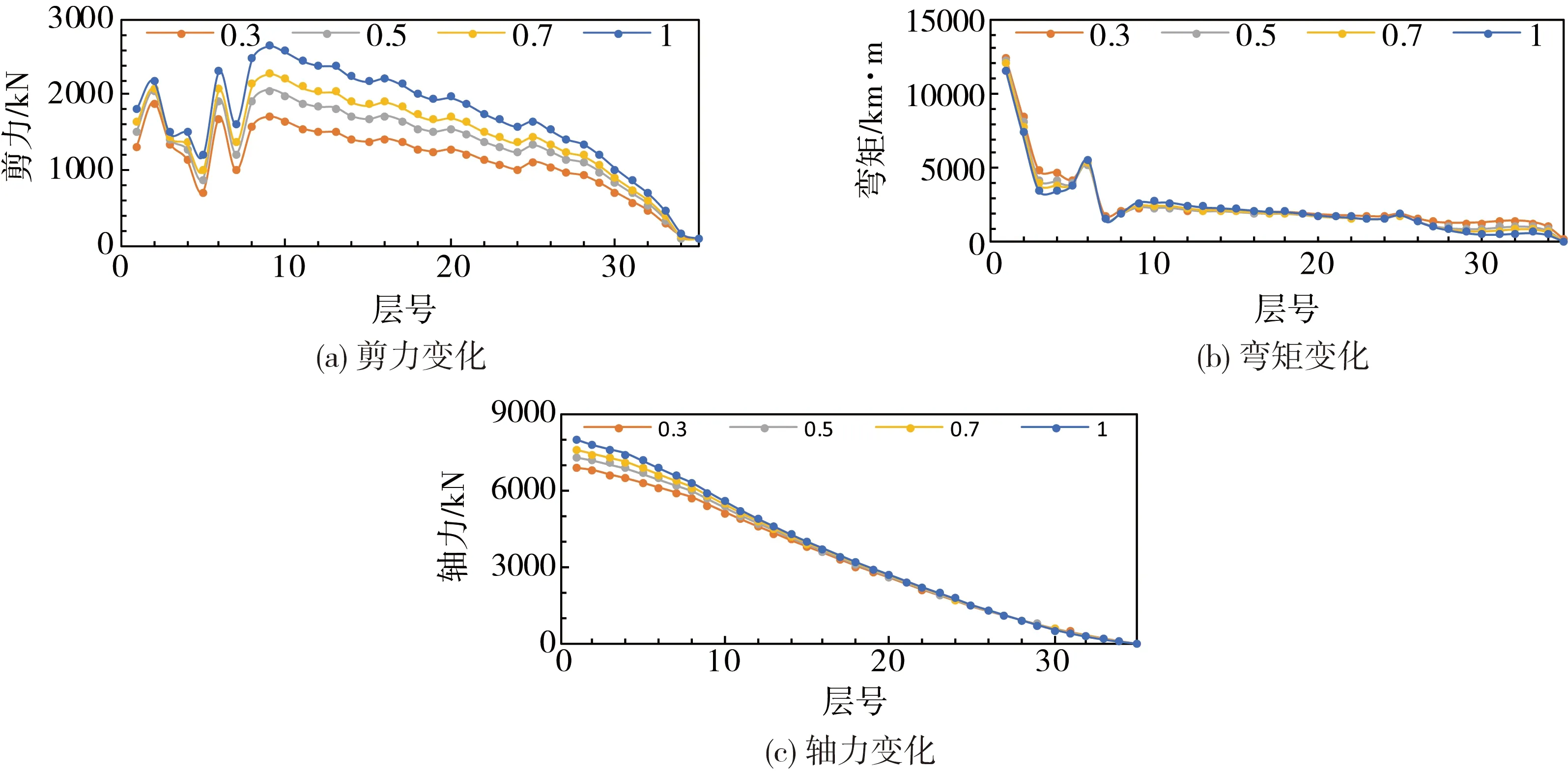
图2 W1剪力墙内力变化Fig. 2 Internal force change of shear wall W1
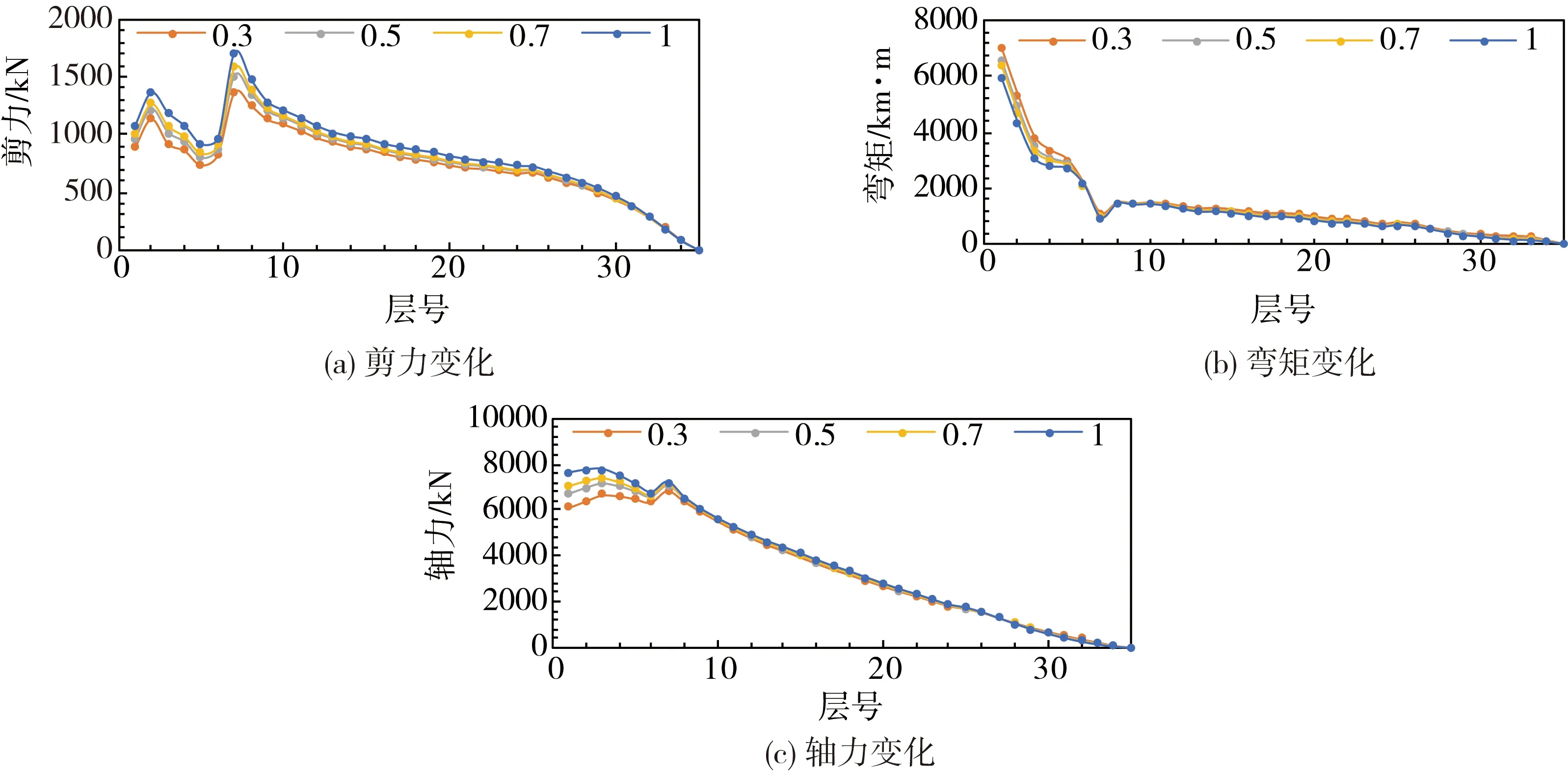
图3 W2剪力墙内力变化Fig. 3 Internal force change of shear wall W2
2 基于弹塑性分析的连梁刚度折减系数
2.1 分析方法
根据文献[11]计算方法,采用SAUSG-Design软件,对9栋剪力墙结构进行弹塑性时程分析,得到弹塑性算法下的连梁刚度折减系数。
弹塑性时程分析根据该结构所处场地类别和设计地震分组各生成一组有代表性的人工地震动进行,地震动峰值加速度根据文献[3]取设防地震对应的加速度值。计算结果见表1“连梁刚度折减系数”,设防地震作用下结构连梁刚度折减系数分布在0.1~1.0之间,离散性较大。
2.2 统计分析
为进一步了解结构基于弹塑性分析的连梁刚度折减系数分布规律,对表1中连梁刚度折减系数进行概率密度统计,得到其概率分布规律,见表1“连梁刚度折减系数概率密度统计”。表6中统计了连梁刚度>0.9、>0.7和<0.5的概率密度。
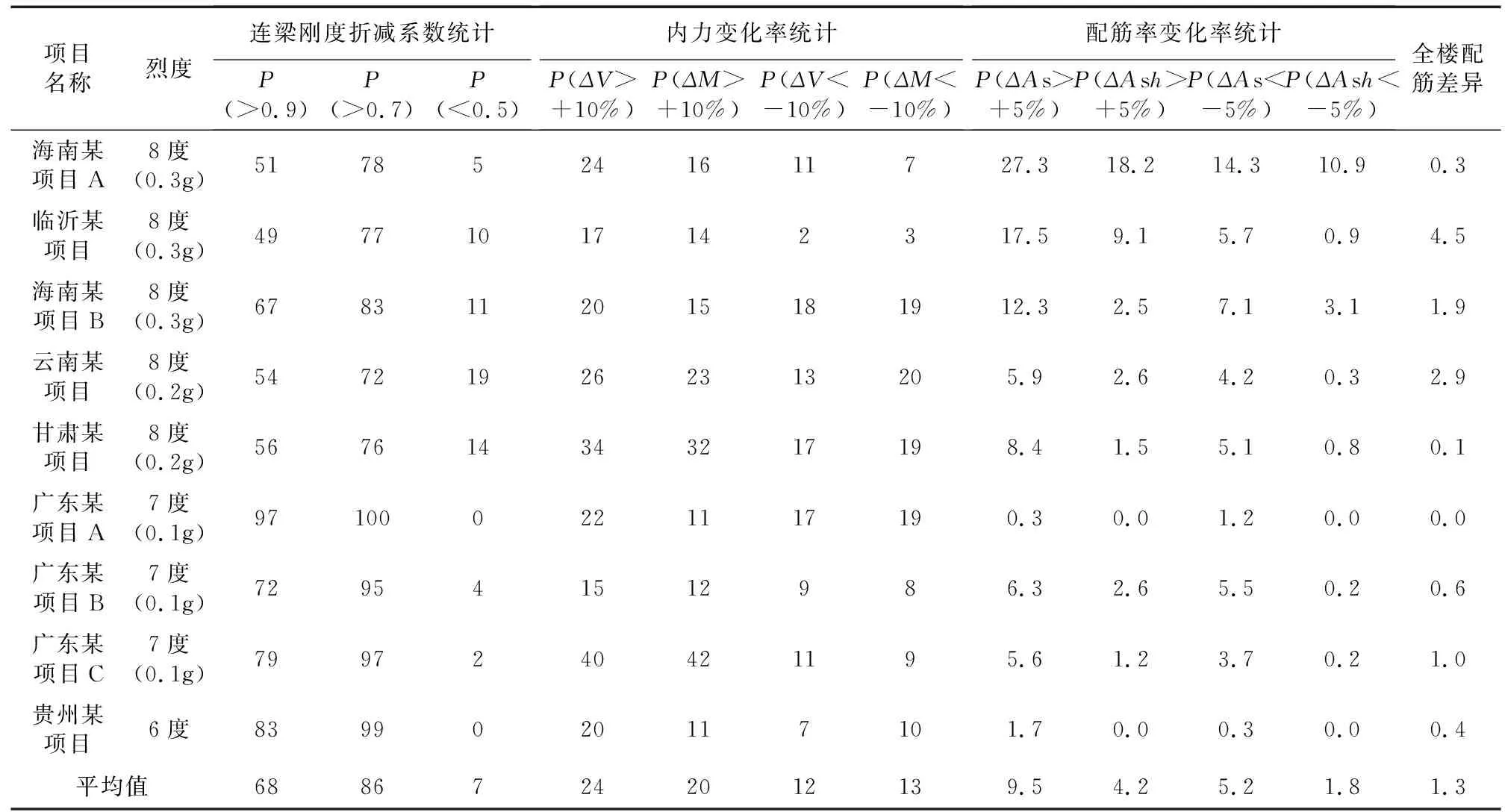
表6 基于弹塑性分析的连梁刚度折减系数模型与全楼统一0.7折减系数模型构件对比Table 6 Comparison of different coupling beam stiffness reduction coefficient model based on elasto-plastic analysis and unified 0.7 coefficient model %
从表6可以看出:不同结构连梁刚度折减系数离散性较大,但大部分处于0.5~1.0之间。对于低设防烈度结构统计结果与规范基本一致,95%以上的连梁刚度折减系数大于0.5;对于高设防烈度结构,存在10%左右的连梁,其刚度折减系数小于0.5,说明“抗规”0.5的连梁刚度折减系数下限基本合理。
当连梁刚度折减系数大于0.9时,说明连梁在设防烈度下处于基本无损坏状态。从表6可以看出:高设防烈度结构有50%左右的连梁处于无损坏或轻微损坏状态;而低设防烈度结构的比例接近70%~80%。可见:全楼设置统一的连梁刚度折减系数会低估50%以上的连梁刚度。
对于剪力墙结构,通常设计时连梁刚度折减系数全楼统一取为0.7。从表6可以看出:连梁刚度折减系数大于0.7的比例接近80%(高设防烈度)和95%左右(低设防烈度),说明全楼采用统一的连梁刚度折减系数,剪力墙结构的刚度模拟存在较大误差的。
3 对结构分析结果影响的统计分析
3.1 整体指标对比统计分析
本文针对上述9栋典型剪力墙结构,从结构基本周期、最大层间位移角和基底剪力等角度,对比分析全楼统一指定连梁刚度折减系数方法与基于弹塑性分析确定连梁刚度折减系数方法的结构整体指标变化情况,如图4所示。基于弹塑性分析的连梁刚度折减系数模型整体刚度变化较大,高烈度区结构接近或大于全楼统一0.7连梁刚度折减系数模型;低烈度区结构整体刚度接近于全楼统一1.0连梁刚度折减系数模型。
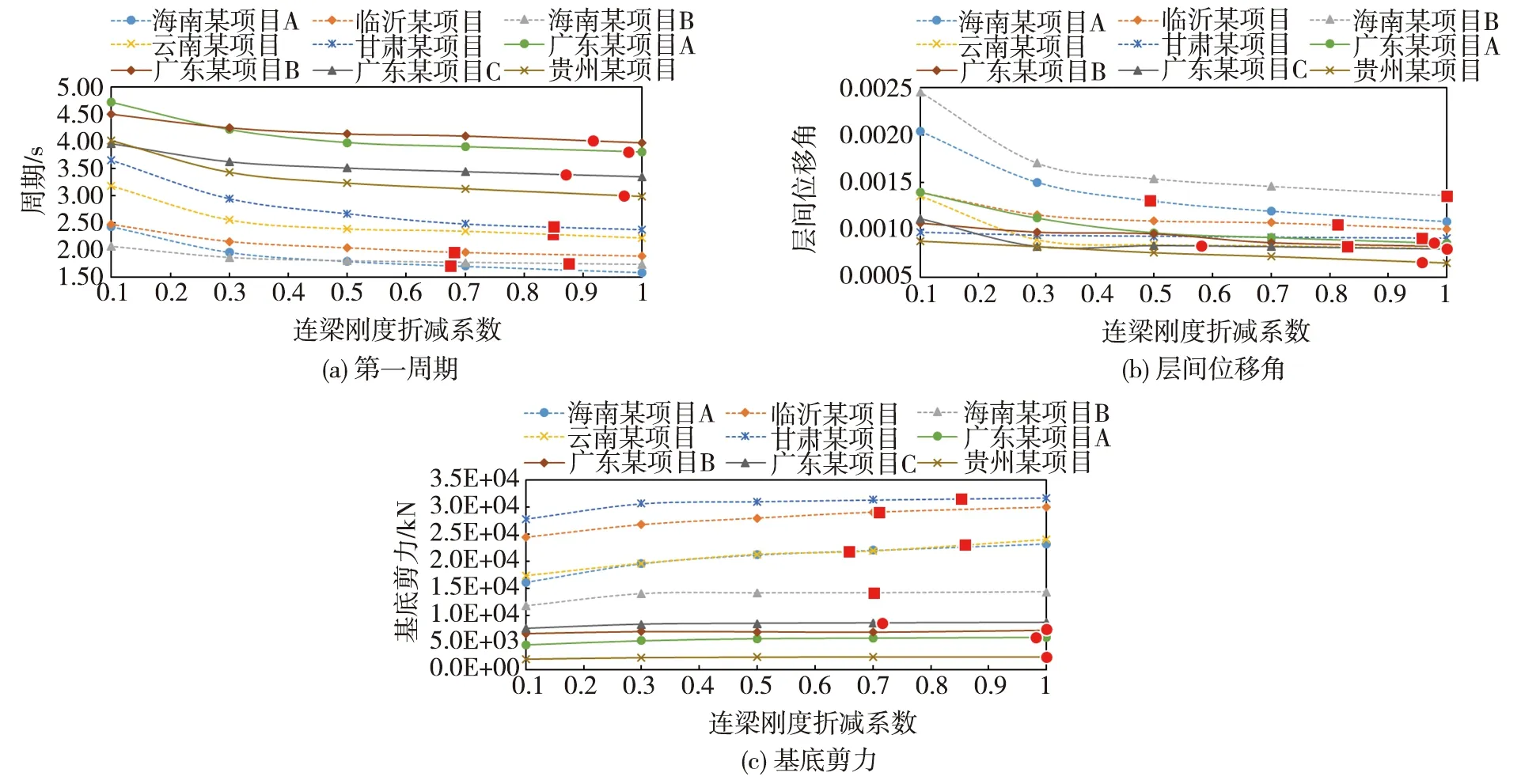
图4 连梁刚度折减系数对整体指标影响(红色点为基于弹塑性分析的连梁刚度折减系数模型计算结果)Fig. 4 Effect of coupling beam stiffness reduction coefficient on overall index (red point is the result of coupling beam stiffness reduction coefficient model based on elasto-plastic analysis)
实际工程结构设计时,普遍采用的全楼统一指定0.7连梁刚度折减系数会人为降低剪力墙结构刚度,使得层间位移角计算结果偏大。一方面由于结构整体平动抗侧刚度的降低导致;另一方面结构的扭转刚度下降也可能导致结构层间位移角偏大。例如,海南某项目B结构标准层基于弹塑性分析的连梁刚度折减系数分布如图5所示,结果表明结构内部连梁刚度折减系数为0.5~0.6,外边线连梁刚度折减系数为0.9~1.0,全楼统一指定0.7连梁刚度折减系数会显著降低结构外框的刚度,导致结构扭转刚度人为降低。

图5 海南某项目B标准层基于弹塑性方法的连梁刚度折减系数分布Fig. 5 Distribution of coupling beam stiffness reduction coefficient for standard floor of Hainan B
低设防烈度剪力墙结构全楼统一指定0.7连梁刚度折减系数时,得到的基本周期、层间位移角和基底剪力与基于弹塑性分析的连梁刚度折减系数方法结果差距较大。基于弹塑性分析的连梁刚度折减系数方法结果与全楼统一指定1.0连梁刚度折减系数结果更接近,即低设防烈度剪力墙结构连梁在设防烈度下基本处于弹性状态,不宜进行连梁刚度折减,否则会人为造成剪力墙结构计算刚度偏小。
3.2 构件内力对比统计分析
采用全楼统一指定连梁刚度折减系数和基于弹塑性分析确定连梁刚度折减系数两种方法,对海南某项目A第W1墙肢各层构件内力进行对比,如图6所示。可以看出:两种方法得到的剪力墙构件剪力差别较大,底部和顶部楼层差异在10%以上,部分楼层剪力差异达到50%。
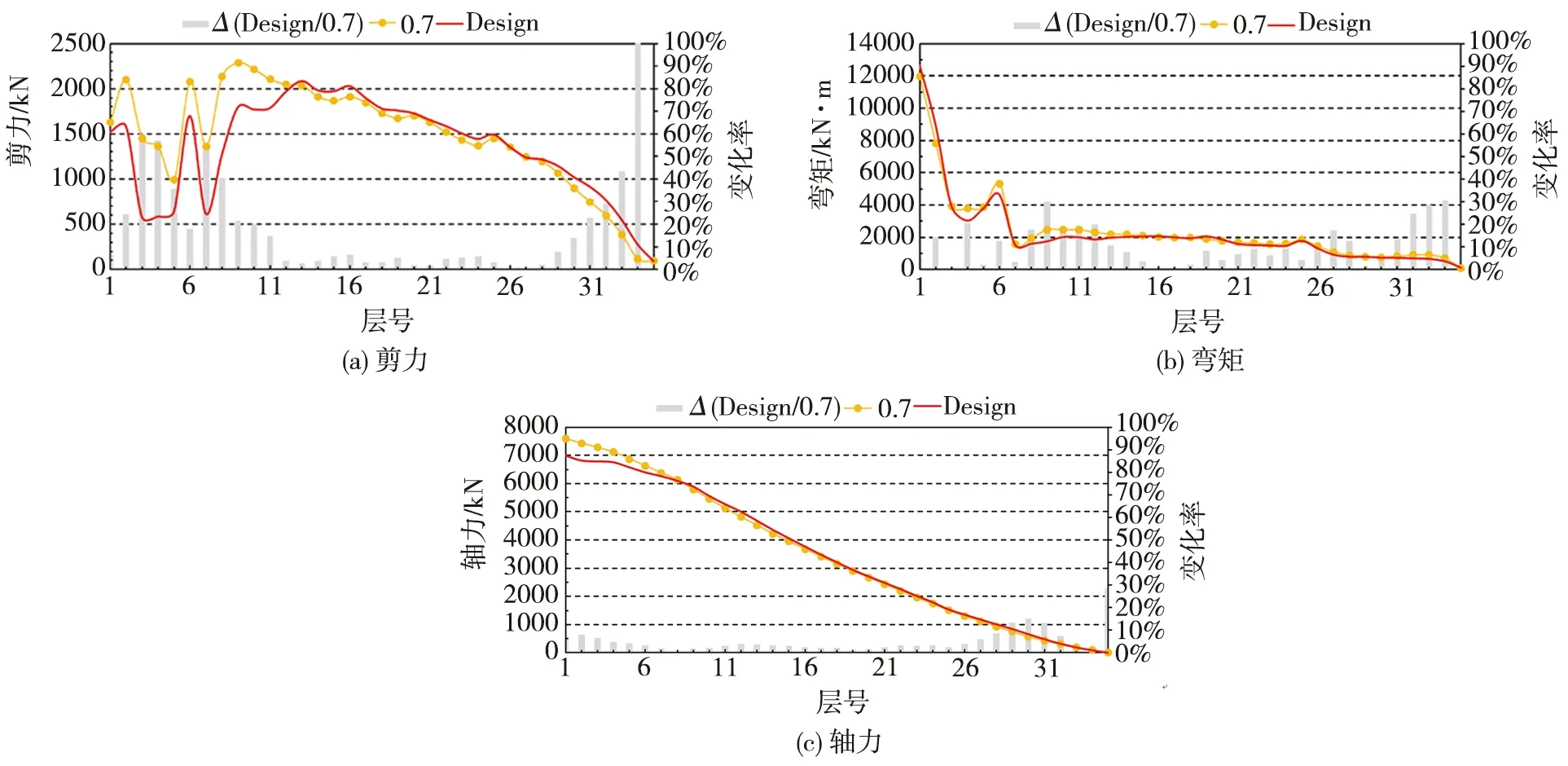
图6 海南某项目模型W1号墙肢内力对比Fig. 6 Internal force comparison of wall W1 of Hainan B
全楼剪力墙地震作用下单工况内力对比见表7,内力变化较大构件数量统计见表6“内力变化率”一列。从9栋剪力墙结构的构件内力分析结果平均值可以看出:结构中50%左右的构件内力变化大于10%,其中平均24%的构件剪力增大超过10%,20%的构件弯矩增大超过10%,同时,存在12%的构件剪力减小超过10%,13%的构件弯矩减小超过10%。说明通过弹塑性分析精确考虑连梁刚度折减系数后,构件内力计算结果会得到明显改善。
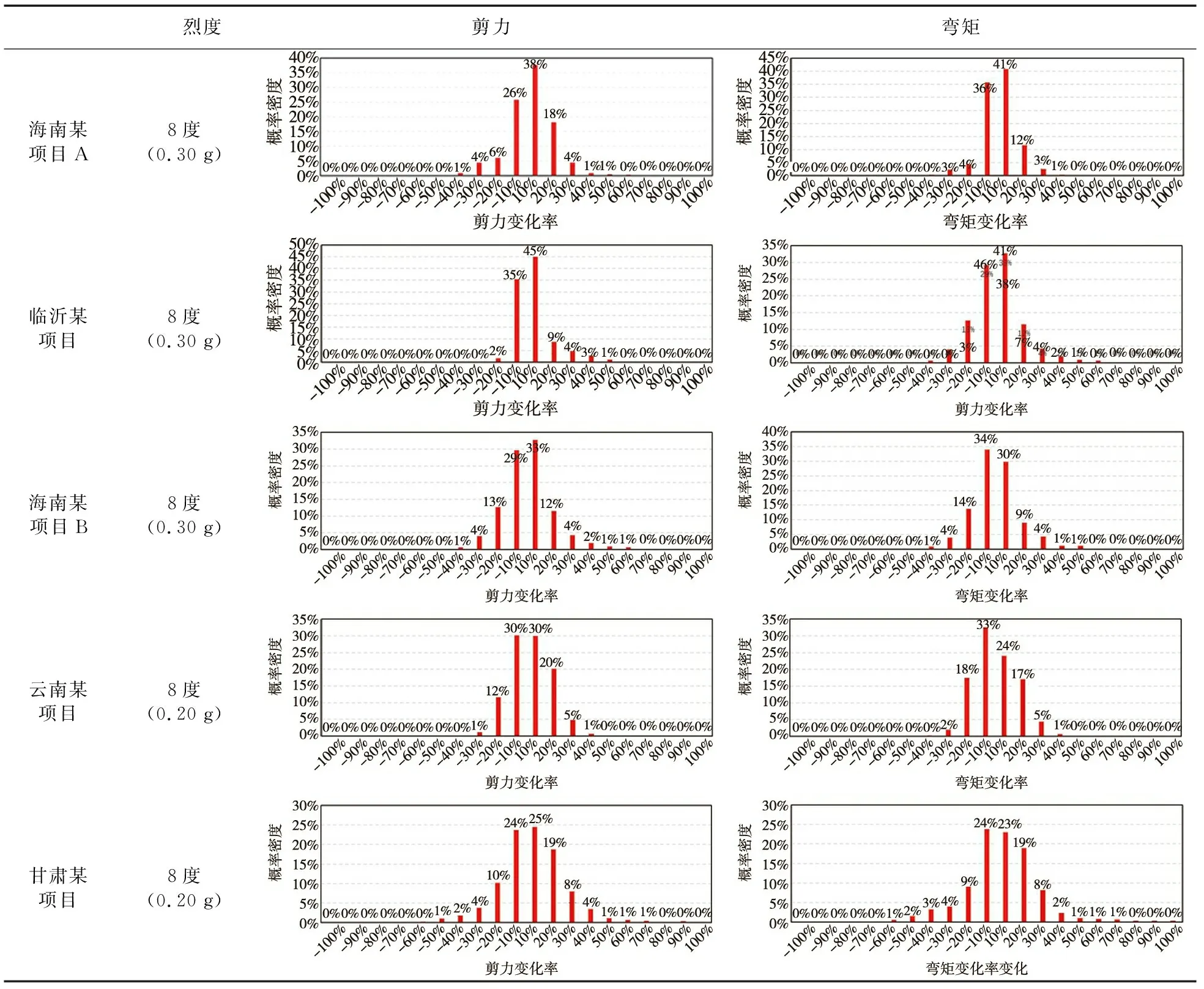
表7 剪力墙内力统计Table 7 Internal force statistics of shear Wall
3.3 构件配筋结果对比统计分析
全楼剪力墙设计配筋变化率对比见表8。结果表明:无论低设防烈度结构还是高设防烈度结构,均存在部分构件配筋变化超过5%情况,高设防烈度结构的构件配筋结果变化更加明显。
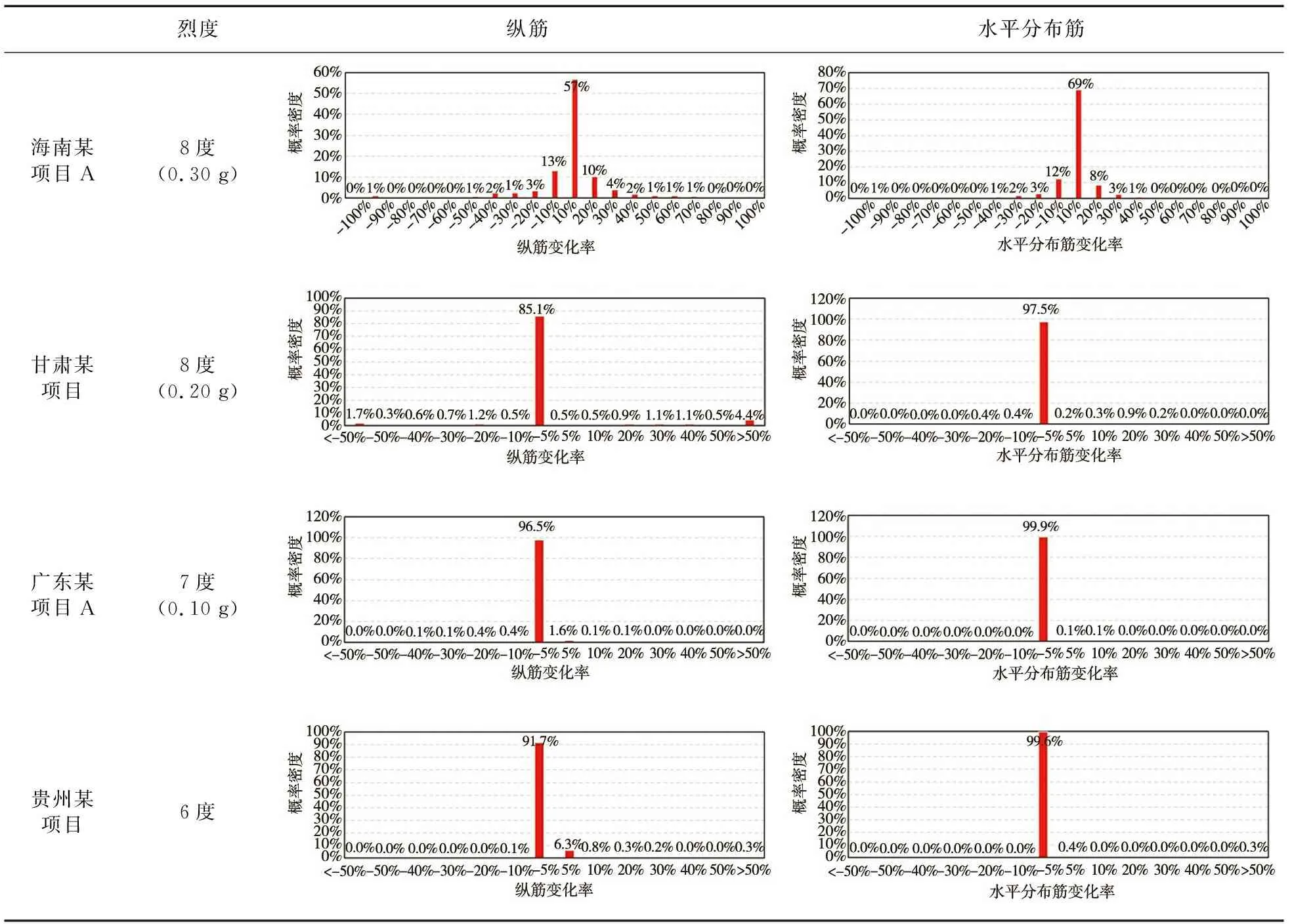
表8 剪力墙配筋变化率统计Table 8 Statistics on variation rate of shear wall reinforcement
对配筋结果变化超过5%的构件进行统计分析,结果见表6。可以看出:结构整体配筋量变化并不显著,但不同部位剪力墙构件配筋结果存在一定差异,配筋量提高的构件数量多于配筋量降低的构件数量。
4 结论
本文针对不同设防烈度的9栋典型高层剪力墙结构,采用全楼统一指定连梁刚度折减系数方法与基于弹塑性分析的连梁刚度折减系数方法进行了对比统计研究,得到以下结论:
1)设防烈度地震作用下,高设防烈度剪力墙结构50%以上和低设防烈度剪力墙结构70%~80%以上的连梁处于无损坏或轻微损坏状态,全楼统一进行连梁刚度折减会造成大量连梁计算刚度失真。
2)从结构基本周期、层间位移角、基底剪力等整体指标以及剪力墙构件内力和配筋等计算结果均可以看出:基于弹塑性分析的连梁刚度折减系数方法均明显优于全楼统一指定连梁刚度折减系数方法。
3)高层剪力墙结构地震响应较大,连梁刚度对结构动力响应影响明显。建议在高层剪力墙结构设计中采用基于弹塑性分析的方法确定结构连梁的刚度折减系数,计算结果更为准确。
4)若采取全楼统一连梁刚度折减系数方法计算,现行规范中“连梁刚度折减系数不宜小于0.50”的规定偏宽松,易造成地震作用计算值偏小。建议地震内力计算时,高烈度区结构(8度及以上),连梁刚度折减系数取值不小于0.70;低烈度区结构(8度以下),连梁刚度折减系数取值不小于0.8。
