深化概念理解 促进模型抽象——《点到直线的距离》素养进阶习题展评与教学建议

文| 陈金波

一、习题展评

●习题一

1.习题内容

（1）涂一涂：将表示点与点、点与线、线与线的“距离”的线段涂成红色。

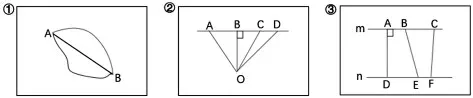
量一量：图①AB 两点的距离是（ ）毫米，图②点O 到直线AD的距离是（ ）毫米，图③两条平行线之间的距离是（ ）毫米。

（2）下图中线段OA 为4 厘米，线段OB 为3 厘米，线段OC为2 厘米，点O 到直线MN 的距离是（ ）。

A.小于2 厘米 B.2 厘米

C.大于2 厘米

2.能力指向

对“距离”的认识。通过涂一涂活动和判断点O 到直线MN 的距离，考查学生对点与点、点与线、线与线的“距离”的认识。

3.学情分析

对乡镇38 名学生进行后测，第（1）小题三个涂色全部正确的人数为34 人（占89.5%），第（2）小题正确的人数为38 人（ 占100%）。大多数学生都能找到点与点、点与线、线与线的“距离”，说明当线处于水平或垂直方向时，学生对距离有较好的认识。

●习题二

1.习题内容

人与高压线的安全距离为50米，“安全距离”我们可看作（ ）之间的距离，并在图中画出表示安全距离的线段。

A.点与点 B.点与线

C.线与线

2.能力指向

能根据现实问题，抽象出点到直线的问题，并抽象出“点”和“直线”。通过寻找人与高压线之间的“安全距离”，发现问题的本质是点到直线的问题。

3.学情分析

从后测情况来看，31.6%的学生选择了点与点之间的距离，63.2%的学生选择了点与线的距离。说明有部分学生无法在真实情境中抽象出点到直线的距离，无法利用点到直线的距离解决实际问题。

●习题三

1.习题内容

小明在四边形的游泳池里游泳，点O 是小明现在的位置。

（1）如果他想在AB 边上岸，请你画出他上岸的最短线路，并用OE 表示。

（2）如果他想在BC 边上岸，请你画出他上岸的最短线路，并用OF 表示。

（3）如果他想尽快上岸，请画出他上岸的最短线路。

2.能力指向

根据已知的点和线段，寻找点到直线的距离。通过画出点O到线段AB、线段BC、线段AD 的距离，考查学生对点到直线的距离的综合应用能力。

3.学情分析

从后测情况来看，点O 到线段AB、线段BC、线段AD 的距离都能正确画出的人数占65.8%。学生的错误集中在画点O 到线段BC 和线段AD 的距离，学生画的不是垂直线段，而是与AB 平行的线段。说明当线不是处于水平或垂直状态时，出错的学生明显增加，得出学生对“距离”的理解还不够。

二、教学建议

1.加强对“距离”的认识

点到直线的距离实质上是点到直线的所有连线中垂直线段最短，所以对“距离”的认识可以从“最短”“唯一” 这两个方面入手。从学生测试情况来看，当线不是处于水平或垂直方向时，学生的出错率较高。为此，在教学时要加强学生对“距离”的概念理解，也要设计相对应的变式练习，提高学生的能力水平。

2.加强对现实问题的模型抽象

点到直线的距离在生活中应用较为广泛，也是后期学习图形的高、轴对称等相关知识的基础。所以对点到直线的距离的认识要加强模型的抽象，能在简单的现实问题中或者在图形中抽象出点到直线的模型。从学生的测试情况来看，学生的抽象能力较弱，对点和线的抽象能力不够。为此，在教学时要加强学生对点和线的认识，提供丰富的素材，提升学生的抽象能力。