Disturbance observer-based fuzzy fault-tolerant control for high-speed trains with multiple disturbances

Qian-Ling Wang(王千龄), Cai-Qing Ma(马彩青), and Xue Lin(林雪),†

1School of Artificial Intelligence,Hebei University of Technology,Tianjin 300131,China

2College of Automation and Electronic Engineering,Qingdao University of Science and Technology,Qingdao 260061,China

Keywords: fault-tolerant control,high-speed trains,disturbance observer,fuzzy logic

1.Introduction

High-speed railway occupies an important position in modern transportation systems due to its advantages of large carrying capacity,fast running speed,high safety,and low energy consumption.At the same time, high-speed trains have become one of the preferred modes of transportation for people because of the comfortable seats, large room, better budget, and nice view outside the window.[1-3]With the continuous increase of the operating mileage of high-speed railways around the world,the safe operation of high-speed trains,which is the fundamental prerequisite and basic guarantee for the rapid development of high-speed railways, has become more and more prominent and poses a great challenge to the design of train driving strategies.[4-7]A very important and convenient way to develop train driving strategy is to establish train dynamics model and to conduct research on this basis.[8]The matching degree between the dynamics model and the actual operating characteristics of the train is a key factor affecting the effectiveness and reliability of the designed train driving strategy.

In order to obtain reasonable train dynamics models and design effective operation strategies, many scholars have carried out a lot of meaningful research.[9-20]Generally speaking, train dynamics models can be roughly divided into two categories: single-particle model and multiple-particle model.In the single-particle model, the train is considered as a rigid body and the elastic dynamics among adjacent carriages are ignored.Based on this method, the influence of external factors including random disturbance, time-varying running resistance and modeling uncertainty on train operation performance can be easily studied.[9-11]On the basis of the single-particle model,different control strategies,such as sliding mode control strategy,[9,12,13]approximation-based robust adaptive control strategy,[14]and backstepping adaptive driving strategy,[15,16]have been proposed to improve the control accuracy of trains.Meanwhile, the multiple-particle model treats each carriage as a particle, so the train can be described as a cascade of single-particles connected by flexible couplers.Compared with the single-particle model, it is more realistic and suitable for designing distributed train control strategies.[17]On the basis of the multiple-particle model,Songet al.[18]provided an advanced operation strategy for high-speed trains subject to traction/braking failures; Zhouet al.[19]considered uncertain parameters and designed a driving strategy based on multiple-model adaptive control with second-level adaptation; Donget al.[20]proposed a sliding mode fault-tolerant control strategy in the absence of actuator faults and bounded parameters.The control strategies based on the single-particle model or the multiple-particle model are proved to be effective and feasible,and can ensure good position and velocity tracking performance.

Based on the above analysis, we find that the singleparticle and multiple-particle models have played a certain positive role in research of high-speed train dynamics modeling and operation control, while there are still some deficiencies in accurately describing the actual dynamic characteristics of the train.They are mainly reflected in two aspects.One is that factors such as rotating mechanical resistance, aerodynamic resistance, external disturbances, and insulated gate bipolar transistor(IGBT)failures are neglected in the modeling process, which may affect the dynamics of the train.The other is that most of the dynamic parameters in the model are assumed to be fixed or time-varying values in a single mode, which makes it difficult to describe the complex and changeable line environment and frequent switching conditions.It is noted that the Takagi-Sugeno (T-S) fuzzy modeling method[21-24]can describe the models of a system in different forms at the same time,and when applied to highspeed trains,it can analyze the influence of different operating states on the train dynamics modeling.Therefore, it is possible to solve the above problems to some extent by modeling train dynamics based on fuzzy logic rules.

The modeling method based on fuzzy logic proposed by Takagi and Sugeno[21,25]has received extensive attention from different scholars all over the world, and has made great research progress in different fields in recent years.[26,27]Tsenget al.[26]proposed a fuzzy tracking control method for nonlinear dynamic systems described by the T-S fuzzy model.Through introducing a reference model, the tracking control problem of two-link robot systems is converted to the stabilization problem of the estimate errors,the reference state and the original state.Wuet al.[27]presented a compositeH2/H∞control to deal with the dynamics modeling problem of hypersonic vehicles.By defining the error between the output vector and the given command,a new function was introduced.The tracking control problem of hypersonic vehicles is also converted to a stabilization problem of the state variables in the overall fuzzy system.Similar techniques can also be found in Refs.[28-32].Although modeling methods based on fuzzy logic have been widely used, they are less common in highspeed train dynamics modeling.[33,34]

However,most of the existing research on automatic train driving technology for high-speed trains relies on the assumption of the single operating state.[35-37]In this case,the stabilization problem based on the fuzzy logic model can be addressed.However, for the tracking problem of high-speed trains, when the position and velocity are both regarded as state variables,the above stabilization method based on fuzzy logic is no longer applicable, and the stabilization problem is meaningless at all.In order to obtain the desired position tracking performances and velocity tracking performance of high-speed trains,the research in the existing literature can be divided into three parts: The first one is the stabilization problem of position tracking errors and velocity tracking errors,in which the desired position and velocity tracking curves are designed.[38]The second is the arrival problem of the sliding mode surface, which implies the stabilization problem of the position and velocity tracking errors.[9,12,20]The third is the stabilization problem of the equilibrium errors, where the position, velocity, and acceleration at the equilibrium are introduced.[35,39]However, these methods can only describe the dynamic characteristics of high-speed trains under a single operating condition, and cannot fully reflect the complex operating environment.Specifically, in the process of train dynamics modeling,the influence of different working conditions is ignored, and the coefficients of the dynamics expression are designed to be in a single scenario.Consequently, it is extraordinary meaningful to model the fuzzy dynamics for high-speed trains.

Through the above analysis, we notice that the research on train dynamics modeling and operation strategy design can be further improved from the following two aspects.First,the accuracy of train dynamics modeling and the degree of matching with the actual operating conditions need to be improved,because the existing models seldom consider the influence of different operating dynamic parameters and speed limit curves under complex operating conditions.Second,in terms of train operation strategy, most of the existing control strategies are based on a single operating parameter,while the fuzzy control strategy based on the T-S model is almost absent.Therefore,in this paper, the problems of dynamical model with fuzzy logic and tracking controller design for high-speed trains subject to actuator faults and multiple disturbances are addressed.According to defining new variables, the multi-mass point model of high-speed trains subject to actuator faults and multiple disturbances can be rearranged as a linear system.Then,the overall fuzzy system of high-speed trains can be obtained.For sake of describing the train operation state in more detail,T-S fuzzy rulers are applied to show the dynamical model under different running parameters.The parallel distributed compensation theory is applied to design the disturbance observer and the fuzzy fault-tolerant controller.The exogenous system is introduced to describe the modeled disturbance,and a disturbance observer is presented to estimate the modeled disturbance.By designing the linear sliding mode surface,the tracking control problem can be rearranged as the arrival problem of the sliding mode surface.Based on the disturbance observer,a fuzzy fault-tolerant control scheme for high-speed trains is presented.Then,the stability of the closed-loop system can be proved by the Lyapunov theory.Simulation results show that the proposed control strategy is feasible and effective.In general, the main contributions of this paper are as follows:

(i) A novel dynamical model with T-S fuzzy rulers is proposed, which can describe different running conditions of high-speed trains.

(ii) The parallel distributed compensation theory is used to design the disturbance observer and controller.Through the linear sliding mode surface with proportional and differential coefficients,the stabilization problem of the tracking error for high-speed trains is transformed to the arrival problem of the sliding mode surface.

(iii)A fuzzy logic-based sliding mode fault-tolerant drive strategy is proposed for high-speed trains subject to actuator faults and multiple disturbances,which can guarantee the desired position and velocity tracking performances.

The rest of the paper is organized as follows:In Section 2,the overall fuzzy system of high-speed trains subject to the interactive forces, the time-varying gusts, the basis running resistances, the aerodynamic resistances and actuator faults is reconstructed.In Section 3,a disturbance observer and a faulttolerant driving strategy are presented,which can be proved to be feasible and effective in Section 4.In Section 5, the conclusion is given.

2.Problem statement and some preliminaries

Without loss of generality,the longitudinal dynamics of a high-speed train withncarriages reads[20,35]

Remark 1 In this paper, the time-varying gusts and the basis running resistance are viewed as multiple disturbances,where the former is the modeled disturbance and the latter is the bounded disturbance.

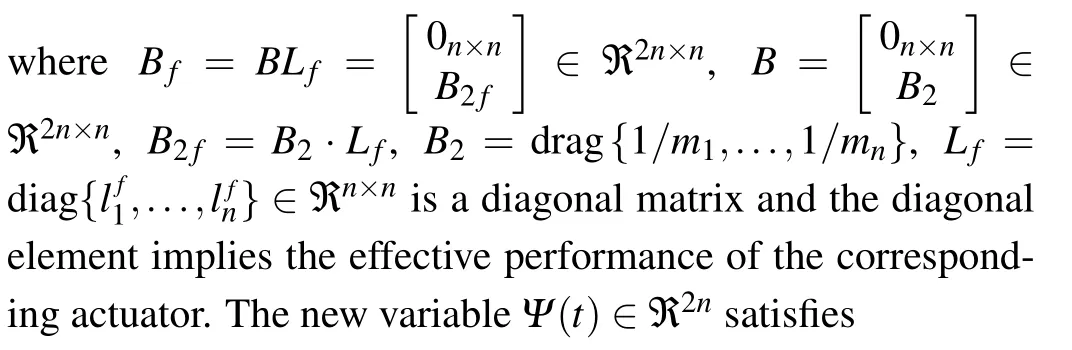
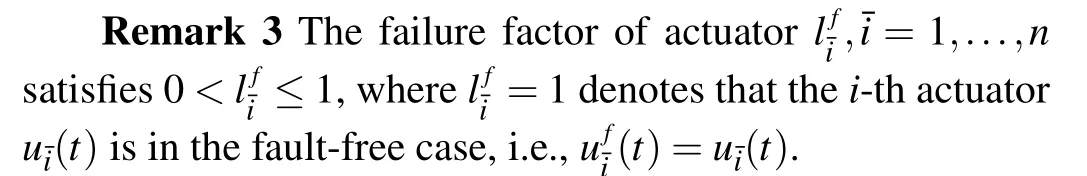
Remark 4 In the new system(2),d(t)can be viewed as the modeled disturbance.Moreover, its amplitude, frequency and phase are designed to be known.

Aiming at the system(2),our objective is to ensure good tracking and velocity tracking performances for high-speed trains subject actuator faults by designing an appropriate operation strategy.However,it is very hard to deal with the nonlinear termΨ(t)during designing the control scheme.Based on this, the system (2) is rearranged as a new linear system by combining with the extraordinary nature of the T-S fuzzy theory.[21,22]Thei-th fuzzy rule of the new linear model is as follows:

Plant rulei

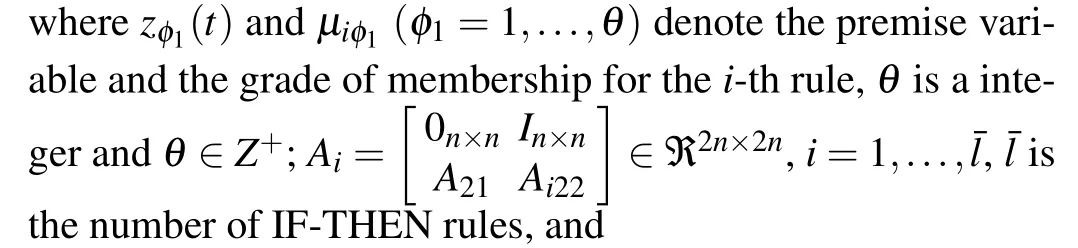
According to the above fuzzy rules,the overall fuzzy system can be written as

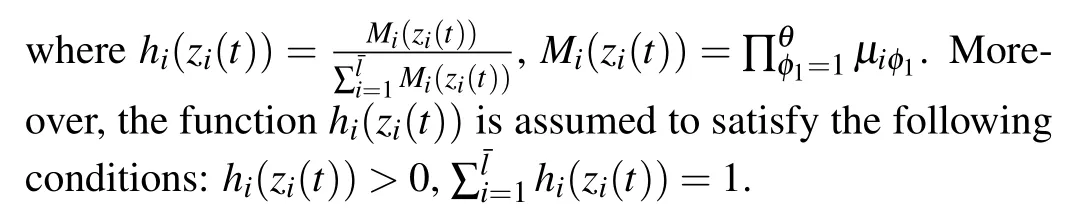
So far,the fault-tolerant controller design problem of the nonlinear system(2)has been transformed into the fuzzy faulttolerant controller design problem of the linear system(4).

To design a reasonable fault-tolerant controller for highspeed trains subject to actuator faults and multiple disturbances,the following assumption lemma can be necessary.

Lemma 1[35]For anyΘ1,Θ2andΘ3, ifΣ(t)ΣT(t)≤Iexists,then the sufficient and necessary condition of

is

whereε0＞0.

3.Main results

In this section, a sliding mode fault-tolerant control scheme which is based on a disturbance observer is proposed to ensure the desired tracking performances for high-speed trains subject to actuator faults.The system block diagram is shown in Fig.1.To guarantee the desired tracking performances for the overall fuzzy system, in this paper we apply the parallel distributed compensation theory[27]to design the control law.

3.1.Disturbance observer design

According to Refs.[40-43],it is reasonable that the modeled disturbanced(t)in the system(4)can be expressed by the following exogenous system:

whereEandFare known matrices;Σ(t) is a known timevarying matrix and satisfiesΣ(t)ΣT(t)≤I.For sake of utilizing disturbance-observer-based control formulation for the exogenous system with the unknown variablew(t),the following assumption is necessary.

Remark 5 In Eq.(6), the matricesWand ΔW(t)are the parameters related to the gust frequency.The latter ΔW(t)implies that the gust frequency is time-varying.

In order to compensate the modeled disturbanced(t)with the unknown state variablew(t),a disturbance observer which is based on Assumption 1 and Eq.(5)is constructed as follows:

where ˆd(t)and ˆw(t)are the estimates ofd(t)andw(t),respectively;Lis the gain matrix to be determined;ν(t) shows the internal state of the disturbance observer, which is generated by

Thus, by combining Eqs.(5), (7) and (8), the new error system can be inferred as

On account of theH∞theory, we can design the performance index function as follows:

whereγ0is a positive constant to be designed.

Aiming at the above exogenous system(5)and the disturbance observer(7),we can summarize the following theorem.

Theorem 1 Consider the error system(9)of the modeled disturbanced(t).The disturbance observer in the form of(7)is effective.If the following cases are guaranteed,For a given positive parameter ¯γ0, the error system(9)will be asymptotically stable withH∞performance index function(10).If there exist a constant ¯ε0＞0 and matricesQ0,P0＞0,the following inequality will holds:

with

Moreover,the gain of the disturbance observer can be calculated by

Proof In order to prove Theorem 1,the following appropriate Lyapunov function is selected for the error system subject tod(t):

which implies

Substituting Eqs.(12) and (13) into the performance index function in the form of(10)yields

with

In consideration of Schur complement and Lemma 1,substituting the inequality (11) into Eq.(14) yields ˘Qw ＜0, i.e.,J ＜0.Hence, the proof of Theorem 1 is completed.To sum up, the disturbance observer in the form of Eq.(11) is effective.

Remark 6 The unknown parameter ¯ε0＞0 and matricesQ0,P0＞0 in Theorem 1 are solved by linear matrices inequality,which can be viewed as known quantities during designing the controller.

3.2.Fault-tolerant driving strategy design

Meanwhile, for the sake of maintaining good robustness of the system, the following sliding mode surface can be designed:

Then,on the basis of the above disturbance observer(7),thei-th rule for the control algorithm can be inferred.

Controller rulej

wherezφ2(t)andµjφ2(φ2=1,..., ¯β)denote the premise variable and the grade of membership for thej-th rule, ¯βis an integer and ¯β ∈Z+;j=1,...,¯l, ¯lis the number of IF-THEN rules.Kjdenotes the controller gain.

Therefore,the T-S fuzzy controller can be rewritten as

Then,the following theorem can be concluded.

Theorem 2 Consider the T-S fuzzy controller (17) and the closed-loop system(16)with the disturbance observer(7).Given the parameter ¯ε0＞0,λ ＞0,if there exist the parameter ¯γsand matricesQj,P ＞0,then the following linear matrix inequalities hold:

with

Then, the closed-loop system is asymptotically stable and all signals of the closed-loop system converge to a ball.

Moreover, if the above conditions are feasible, then the gain of the controller(17)can be calculated by

Proof To verify the feasibility and effectiveness of the control strategy(17),an appropriate Lyapunov function is selected as

wherePis a positive definite matrices;P0＞0 can be defined in Theorem 1.Thus,along the trajectories of(16),substituting the disturbance observer(7)and the adaptive law(17)into the time derivative of(20)yields

where sym(·)=(·)+(·)T,the symbol(·)replaces any matrix.

with

whereζis a positive constant and satisfiesδT(t)δ(t)≤ζ/.

Hence,the solution of the inequation(23)can be derived as follows:

whereV(0)=ST(0)PS(0)+ ˜wT(0)P0˜w(0).

Combining Eqs.(20) and (24), we can have 0＜V(t)≤ζ/λ,which implies

where ¯λ(·) denotes the maximum eigenvalue of a matrix.Thus,we obtain that the signals of the closed-loop system converge to a ball,whose radii are decided by Eq.(25).The proof is completed.

Remark 7 According to Theorem 2 and Eq.(25), it is noted that the size of|S(t)|and|˜w(t)can be freely adjusted by the design parametersλ,ζand matricesP,P0.

Remark 8 Based on the proposed disturbance observer and the fuzzy fault-tolerant controller, the tracking control problem is transformed into the problem of solving inequalities.Moreover,if the parameterλ,the characteristic roots ofPandQbecome smaller,then the convergence performances of the closed loop system will be reduced.Conversely, if the parameterζbecomes smaller, then the convergence performances of the closed loop system will be improved.

Remark 9 From Refs.[35,36], the gusts can be calculated as a cosine function.Consequently,it is reasonable that the gusts are viewed as the harmonic signal.

Corollary 1 Given the dynamics of high-speed trains(1)without actuator faults and based on the following disturbance observer:

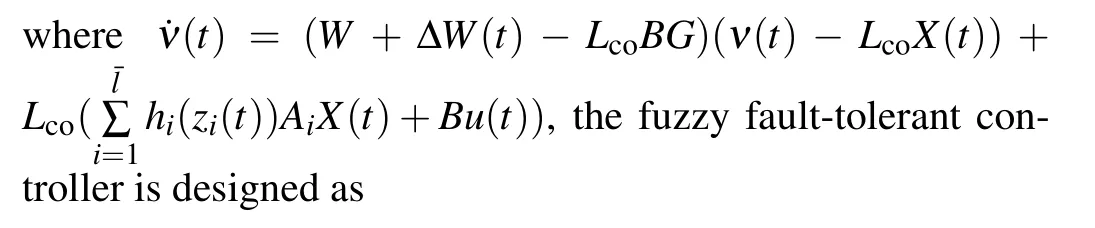
whereKjdenotes the controller gain.With given parameters¯ε0,co＞0,λco＞0,P0,co＞0, if there exist the parameter ¯γs,coand matricesQj,co,Pco＞0, then the following linear matrix inequalities hold:

with

Then, the closed-loop system is asymptotically stable and all signals of the closed-loop system converge to a ball.

Moreover, if the above conditions are feasible, then the gain of the controller(17)can be calculated by

The proof of Corollary 1 can refer to Theorem 2, which is omitted here.

4.Simulation results

Combining with the parallel distributed compensation theory, one can take the solutions of the inequality (11) in Theorem 1 as a known quantity and substitute them into the inequality(18)in Theorem 2.Then,one can obtain

Fig.2.Desired position and velocity tracking curves for high-speed trains.

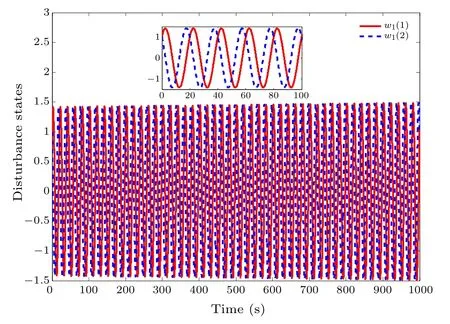
Fig.3.The modeled disturbance states.

On the basis of the above simulation conditions, the desired running curves and the modeled disturbance states are shown in Figs.2 and 3.We define the initial value of the system and the disturbance observer as 0.To compensate the modeled disturbance,the disturbance observer is designed,whose states can be described as shown Fig.4, which proves that the proposed disturbance observer in Eq.(7) can well estimate the harmonic interference signal, i.e., the proposed disturbance observer is feasible and effective.Figures 5-8 describe the running curves of high-speed strains with the proposed fault-tolerant control scheme.Here, Figs.5 and 6 demonstrate the position tracking errors of high-speed trains,and Figs.7 and 8 demonstrate the velocity tracking errors of high-speed trains,which imply that the actual position and velocity curves can track the desired position and velocity curves well, i.e., the presented control scheme is feasible and effective.Comparing Figs.5 and 6 with Figs.7 and 8,we can obtain that the convergence time of velocity tracking error is shorter than that of position tracking error of carriagei,i=1,2,...,8.

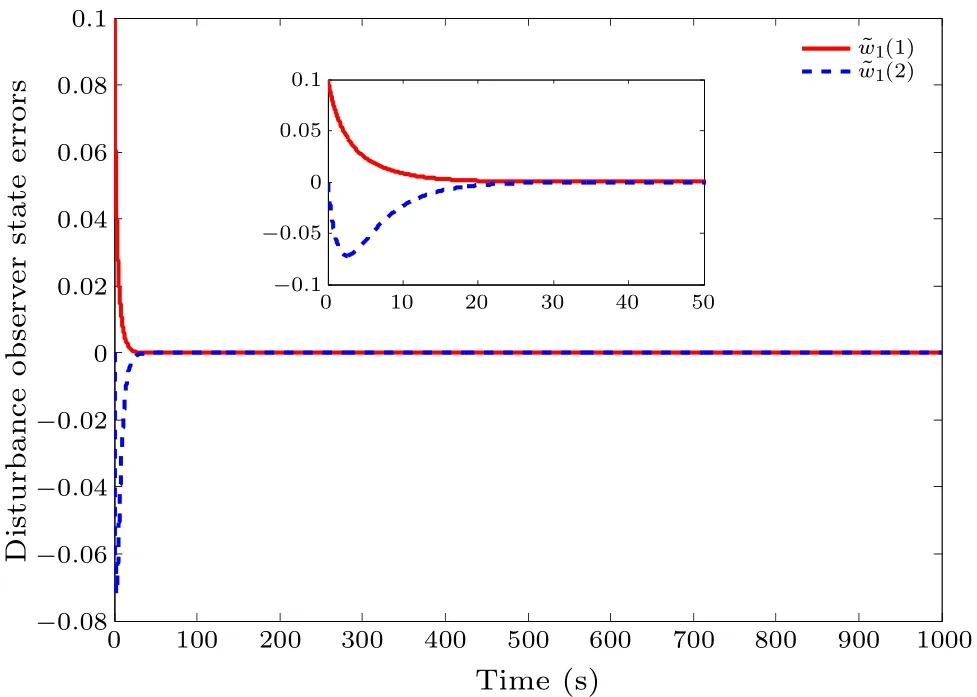
Fig.4.State estimate error curves for the disturbance observer.

Fig.5.Position error curves of the i-th carriage for high-speed trains,i=1,2,3,4.

Moreover, comparing the simulation results with the robust adaptive nonsingular terminal sliding mode control scheme in Ref.[9]for the same parameter settings,such as the total mass and Davis’ coefficients, we can obtain that in this paper the position tracking accuracy and the velocity racking accuracy can be increased to 10-5and 10-4.Consequently,we can reach the higher tracking accuracy of position and velocity by using the proposed fuzzy fault-tolerant driving strategy of high-speed trains.

Fig.6.Position error curves of the i-th carriage for high-speed trains,i=5,6,7,8.

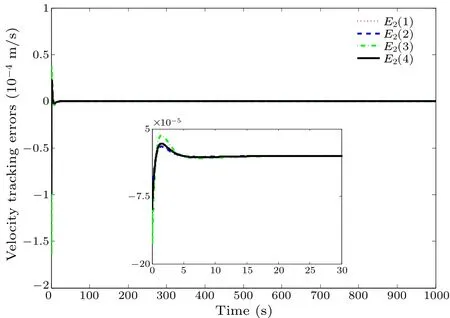
Fig.7.Velocity error curves of the i-th carriage for high-speed trains,i=1,2,3,4.

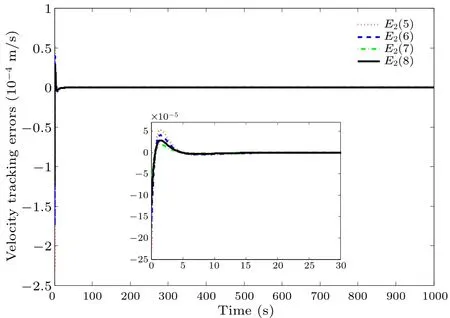
Fig.8.Velocity error curves of the i-th carriage for high-speed trains,i=5,6,7,8.

5.Conclusion

In this paper, a novel dynamical model with Takagi-Sugeno fuzzy rulers is proposed for high-speed trains subject to actuator faults and multiple disturbances, which is based on the traditional multi-mass point model.To compensate the modeling disturbance,the exogenous system whose states are unknown is introduced.The disturbance observer is designed to observe the unknown states.Combining the disturbance observer and the parallel distributed compensation theory,we propose a controller rulers-based T-S fuzzy fault-tolerant drive strategy for high-speed trains with actuator faults and multiple disturbances.The feasibility and effectiveness of the disturbance observer and the drive scheme can be proved by simulation results.In the near future, research of the cooperation fault-tolerant control for multiple high-speed trains will be conducted,based on the proposed fuzzy fault-tolerant control scheme.

Acknowledgment

Project supported by the National Natural Science Foundation of China (Grant Nos.62203246, 62003127, and 62003183).