Fully relativistic many-body perturbation energies,transition properties,and lifetimes of lithium-like iron Fe XXIV

Shuang Li(李双), Min Zhao(赵敏), Guo-Qing Liu(刘国庆),Chang-Bao Hu(胡昌宝), and Guo-Zhu Pan(潘国柱)

1School of Electrical and Opto-electronic Engineering,West Anhui University,Lu’an 237012,China

2College of Mechanical and Electronic Engineering,Fujian Agriculture and Forestry University,Fuzhou 350002,China

3Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

4Shanghai EBIT Laboratory,Institute of Modern Physics,Department of Nuclear Science and Technology,Fudan University,Shanghai 200433,China

Keywords: relativistic many-body perturbation,multi-reference configuration,radiative rates,lifetime

1.Introduction

In recent years, people have shown great interests in lithium-like (or Li-like) ions (with only three electrons outside the nucleus).[1-5]Studying these ions can aid in the exploration of fundamental physics,such as QED effects.[1,2,4,5]Additionally, due to the simplicity of the electronic structure of the ions thus the relatively accurate spectral data,the spectral lines of lithium-like ions can be used for spectral calibration.Furthermore, they can also be used for spectral line identification,[6]as well as for electron temperature, density,and chemical composition diagnostics.[7-9]

The spectra of lithium-like ions have been widely observed in astrophysical and laboratory plasmas, as noted in Refs.[7-9].For example, the spectra of the lithium-like iron have been observed in the solar corona,[10,11]laserproduced plasmas,[12]tokamaks,[13]and electron-beam ion traps.[14,15]Furthermore, the spectra of the lithium-like iron have been observed up to high levels withn=6, as reported in Refs.[11,12,15].

Due to the importance of lithium-like ions, there have been many studies on the ions.[3,6-9,16-30]

In particular, Naharet al.[28](hereafter referred to as Nahar1999) used the quasi-relativistic Breit-PauliR-matrix method (BPRM) to calculate E1 transition radiative rates between energy levels up ton= 10 for lithium-like iron.In their calculations, they just added one-body relativistic correction terms to the non-relativistic Hamiltonian,[31]which included the one-body mass correction, the one-body Darwin term, and the spin-orbit term, they did not even include the two-body interactions in the Breit-Pauli approximation(such as the spin-other orbit, spin-spin, orbit-orbit, two-body Darwin, and spin-contact terms).[32,33]However, when considering the iron ion, it is crucial to incorporate relativistic effects right from the beginning,[34]and the fully relativistic Dirac formalism, which is employed in the present research,is essential.[35]Aggarwalet al.[8](denoted as Aggarwal2012)used the GRASP0 program originally developed by Grantet al.[36]and revised by Norrington to calculate the E1,M1,E2,and M2 transition radiative rates between the lowest 24 energy levels withn ≤5 for lithium-like ions (Z= 21-28, including iron ion).However, the findings of Aggarwal2012 were insufficient in identifying or synthesizing the observed spectra involving then=6 energy levels.Therefore, it is crucial to enhance the results of Aggarwal2012 by further incorporating then=6 energy levels in the calculations, as demonstrated in the present study.In 2016, El-Maaref[24](denoted as El-Maaref2016)provided lifetimes of 1s2nlconfigurations(wheren=2-6 andl=0,...,n-1)for lithium-like iron,but did not report the results for 6f7/2,6g9/2,6h9/2,and 6h11/2levels.El-Maaref used the fully relativistic multi-configuration Dirac-Hartree-Fock(MCDHF)method,[37]which was implemented in the fully relativistic atomic structure program package GRASP2K.[37]Through the procedure of configuration interaction(CI),the relativistic effects such as Breit Hamiltonian and quantum electrodynamics effects (QED) were included,and the considered configuration state functions(CSFs)were from all single-(S) and double-(D) excitations (or substitutions)up to 7l,and single-(S),double-(D),and triple-(T)excitations up to the 6lorbitals.

However, unfortunately, although El-Maaref2016 employed an advanced fully relativistic method (MCDHF),the lifetimes of El-Maaref2016 in the “Table 3”[24]are significantly different from the fully relativistic lifetimes of Aggarwal2012[8]and the quasi-relativistic ones of Nahar1999.[28,38]For example,among the 30 reported lifetime values,20,14,10,and 7 have differences with Nahar1999 exceeding 2%, 5%, 10%, and 20%, respectively.The lifetime differences for the 1s24f5/2and 1s26s1/2levels are even up to one order of magnitude, which is quite astonishing! On the other hand,the lifetime values from Aggarwal2012 are almost identical to Nahar1999 ones, with most lifetimes agreeing within 1%,and all within 2%.

Although a fully relativistic method was used in Aggarwal2012, however, the employed program was an early version of GRASP0,[36]besides, the configuration interactions were only limited to withinn ≤5 levels.Thus the lifetime values maybe have some deviations.On the other hand,El-Maaref2016 utilized the latest version of GRASP, called GRASP2K,[37]which is an advanced fully relativistic implementation.Furthermore, larger configuration interactions up to withinn ≤7 levels were considered in El-Maaref2016.Therefore,the newly reported fully relativistic lifetime values from El-Maaref2016 are possibly even the most accurate ones.However, the significant differences between El-Maaref’s results and the ones from both Aggarwal2012 and Nahar1999 cannot be disregarded.

To address the larger discrepancies of El-Maaref2016,here,we employ the advanced relativistic configuration interaction (RCI) combined with many-body perturbation theory(MBPT) method (RMBPT for short), which has been implemented in the FAC code,[39]we provide energies and lifetime values for the lowest 35 energy levels from the 1s2nlconfigurations (wheren ≤6 andl=0,...,n-1) of Li-like iron Fe XXIV, as well as complete data on the transition wavelengths, radiative rates, absorption oscillator strengths, and line strengths between the levels.The transitions include both allowed (E1) and forbidden (magnetic dipole M1, magnetic quadrupole M2,and electric quadrupole E2)ones.

Furthermore, to delve deeper into the evaluation of the present RMBPT results, we additionally utilize the multireference configuration Dirac-Hartree-Fock (MCDHF) combined with the RCI method (MCDHF/RCI for short) as implemented in the GRASP2K code (version 2018[40]).In recent years,we have successfully applied both the RMBPT and MCDHF/RCI methods to the highly accuracy studies of Nilike,O-like,F-like,and Ne-like ions.[41-44]

2.Calculations

For the RMBPT calculations,we employ the widely used flexible atomic code (FAC),[39]elaborate descriptions of the RMBPT method can be found in references.[27,45-47]Therefore,we will not delve into the theoretical aspects in great detail here.Instead, we will offer an overview of the parameter settings for the present RMBPT computations.The Hilbert space is divided into two subspaces: the model space M (CI effects are exactly treated)and the orthogonal space N(CI effects are treated in the second-order perturbation way).The M space contains all the levels from the(1s2)nlconfigurations(where the principal quantum numbern=2-8 and the angular quantum numberl=0,...,n-1).The orthogonal space N consists of single-(S)and double-(D)substitutions from the M space,with the highest S-substitutions up ton=200,and the highest first and second electrons of the D-substitutions up ton=200 andn＇=80,respectively.

To further evaluate the accuracy of present RMBPT results, we also perform MCDHF/RCI calculations for the ion using the GRASP2K package(version 2018[40]).After carrying on the relativistic self-consistent field procedure,we determine both the radial parts of the Dirac orbitals and the expansion coefficients of thej j-coupled configuration state functions(CSFs)expansions,and then in the following RCI calculation,the Breit interaction is considered in the low-frequency limit by multiplying the frequency with a scale factor of 10-6.In the present RMCDHF/RCI calculations,the multi-reference(MR) configuration sets are from (1s2)nlwithn=2-6 andl=0,...,(n-1),namely,for even parity,the MR sets include 2s,3s,3d,4s,4d,5s,5d,5g,6s,6d,and 6g,while for odd parity,the MR sets include 2p,3p,4p,4f,5p,5f,6p,6f,and 6h.For Li-like ions with just one electron outside the 1s closed shell, consequently there is no outer correlation.[48]The correlation corrections to the Dirac-Fock results can therefore be categorized as core-valence (CV) and core-core (CC) types(i.e.both the S-and D-substitutions are allowed).[48]Both the CV and CC correlations are important for highly accurate radiative parameters.[48,49]For instance, it has been shown that the CC correlations can enhance the line strength of the 2s-2p resonance line in the lithium atom by approximately 0.6%.[48]In the present case, our tests show that the CV and CC correlations indeed contribute to line strength corrections of up to 0.7%for the 2p1/2-6d3/2transition and up to 1.3%for the 2p1/2-6s1/2transition, respectively.However, the impact of CV and CC correlations becomes prominent for certain Δn=0 transition rates with low transition energies.For instance,the CV and CC correlations contribute to corrections of approximately one order of magnitude for the 5f7/2-5g7/2transition and around two orders of magnitude for the 6g9/2-6h9/2transition, respectively.However, it should be noted that these Δn=0 transitions are not the primary radiative decay channels for the upper levels.Hence, the impact of both CV and CC correlations on the lifetimes are limited, with maximum impacts of 1.7% for the CV correlation and of 0.8% for the CC correlation,both for the 2p1/2level.For this simple Li-like atomic system with only three electrons,as did in the previous studies,[48,50]we can further include the second-order correlations effects[51]by relaxing the substitution rules to generate all possible CSFs,which means all the three electrons can be substituted in the present case (i.e.all the S-, D-, and Tsubstitutions are permitted),the calculation is said to be a complete active space(CAS)calculation.[34]In our final CAS calculation, by allowing all the S-, D-, and T-substitutions from the MR configurations to active sets up ton=7, andjup to 9/2 and 11/2 for even and odd parities, respectively, which produces 101767 and 123182 CSFs expansions.

3.Results and discussion

3.1.Energies

Table 1 provides the energy values from both present RMBPT and MCDHF/RCI calculations, as well as other theoretical and NIST (National Institute of Standards and Technology) values.The NIST team has meticulously compiled and evaluated energies and other atomic data, and their recommended results can be accessed for free on their website at https://physics.nist.gov/PhysRefData/ASD/levels form.html.Figure 1 shows comparisons between these theoretical energy values and the NIST ones, to make the figure clearer and in detail, the original energy ratio of Key=2 and 3 (i.e., 2p1/2and 2p3/2levels) from Nahar1999 are +0.01 and-0.015,respectively.

Table 1 and figure 1 reveal relatively large deviations between the energies of Nahar1999[28,38]based on the quasirelativistic Breit-Pauli theory and the NIST ones, with majority of the energy differences falling within the range of 0.3%-0.4%.Notably,the largest deviations occur for the 2p1/2and 2p3/2levels, with deviations of approximately 1.5% and 1.9%,respectively.In contrast,the GRASP2K results from El-Maaref2016[24]and the GRASP0 results from Aggarwal2012 demonstrate good agreements with the NIST energies, with most results matching within 0.03%.The deviations for the 2p1/2and 2p3/2levels are slightly larger, around 0.1% and 0.05%for El-Maaref2016,and around 0.4%and 0.2%for Aggarwal2012.The present MCDHF/RCI results exhibit similar agreement with the NIST ones,with the deviations for the 2p1/2and 2p3/2levels being around 0.1%-0.2%.Finally, the present RMBPT results demonstrate the best match with the NIST energies, most within 0.03%, and all within 0.05% including those for the 2p1/2and 2p3/2levels.Regarding the energy levels of lithium-like iron Fe XXIV, there have been many studies.In general, the experimental energy level data from National Institute of Standards and Technology(NIST)is highly precise,which is why we primarily focus on comparing with them.However,it is worth mentioning that for the 2p1/2and 2p3/2levels, the energies obtained from literatures[30,52]are actually the preferable theoretical ones, particularly the highly accurate results from reference,[30]although they are limited to then ≤2 levels.However, for then=3-6 levels,the present RMBPT energies should be favored.

We also investigated the configuration interaction(CI)on the energies,three different CI modes are considered here,i.e.RCI1,RCI2,and RCI3.The RCI1 and RCI2 represent the calculations without and with considering configuration interaction between the(1s2)nl(n ≤6)levels,respectively,while the RCI3 represents the consideration of configuration interaction between more levels withn ≤8.For clarity, the corresponding results from the three modes are not presented in Table 1 or Fig.1.

Furthermore, most of the RCI1 energies agree with the NIST values within 0.05%.However,the agreement is slightly worse for the 2p1/2and 2p3/2energy levels, with discrepancies of around 0.36% and 0.21%, respectively.Nevertheless,when considering configuration interaction within then ≤6 levels (i.e.the RCI2 mode), the agreements with the NIST values improve significantly.For example, the discrepancies decrease to 0.26% and 0.16% for the 2p1/2and 2p3/2levels,respectively,and become negligible(within 0.05%)for all the other levels.Further consideration of CI between more levels withn ≤8(i.e.the RCI3 mode)does not result in significant energy corrections,with the agreements with the RCI2 values being within 0.01%,meaning that the convergence of energies from the relativistic configuration interaction (RCI) methods is relatively slow.To consider configuration interactions between even more levels, the RMBPT method can be utilized.Our RMBPT results demonstrate further improvements of the energies compared to the RCI3 results.Specifically, the two lowest levels exhibit energy corrections of 0.22%and 0.11%,respectively, then=6 levels demonstrate corrections of approximately 0.01%, and the corrections are below 0.01% for the other levels.

The above comparisons show that the present RMBPT energies are highly accurate, and that CI effects are important,especially for the two low lying levels of the ion.

3.2.Radiative rates

Table 2 provides radiative data for dipole allowed (E1)and forbidden transitions (magnetic dipole M1, magnetic quadrupole M2, and electric quadrupole E2) of Li-like iron using the RMBPT method.The data includes wavelengthsλi j(in unit °A),radiative ratesA(in unit 1/s),absorption oscillator strengthsf(dimensionless),and line strengthsS(in unit a.u.), where 1 a.u.=6.460×10-36cm2·esu2.Here, we just present a partial set of data as an example,with the complete data available in electronic form on the website addresses data DOI, data private access link, data anonymous private link,and data CSTR.

It is important to note that our RMBPT energy values agree best with those of NIST, resulting in good agreements between our RMBPT wavelengths and the observed ones compiled by NIST.In fact, both our RMBPT wavelengths for 2s1/2-2p1/2and 2s1/2-2p3/2transitions agree with the observed ones to within 0.05%.However, for transitions with small energy differences (Δn= 0), particularly those with high principal quantum numbers (n=5,6), the corresponding wavelengths may be less accurate, these inaccuracies can propagate to the radiative rates,leading to further inaccuracies.This phenomenon is quite common for any theoretic radiative rates from each method.

Table 2.Transition properties for dipole allowed(E1)and forbidden ones(magnetic dipole M1, magnetic quadrupole M2, and electric quadrupole E2)from present RMBPT methods for lithium-like iron Fe XXIV.Parameters i and j are the lower(i)and upper(j)levels of a transition as defined in Table 1, λi j is transition wavelength (in unit °A), A is radiative transition rate(in unit 1/s), f is absorption oscillator strength(dimensionless),S is line strength in atomic unit (a.u.), and a±b ≡a×10±b.Note: only a portion of transition data are presented here,the complete dataset are in an electronic form on the website of this journal data DOI,data private access link,data anonymous private link,and data CSTR.

In Fig.2, we compare present RMBPT radiative rates with our MCDHF/RCI results and results from previous literatures.Figure 2(a) for dipole allowed (E1) transitions, and figure 2(b)for forbidden(M1,M2,and E2)ones.

For E1 transitions,as can be seen from Fig.2(a),present RMBPT radiative rates are in good agreement with our MCDHF/RCI results, as well as with the results from Aggarwal2012 and Nahar1999.For instance,the radiative rates calculated by present RMBPT and MCDHF/RCI show a high degree of agreement,with deviations below 1%for all the Δn/=0 transitions,except for the 2p1/2-6s1/2transition,for which the deviation is around 2%.Moreover, for most Δn=0 transitions,the deviations between the two sets of radiative rates are below 2%.Nonetheless, for two specific Δn=0 transitions,namely 5f7/2-5g7and 6f7/2-6g7/2,the deviations reach up to a factor of 5.These deviations mainly arise from discrepancies in the wavelength determinations, as both the strengths from the two data sets are in agreements within 2%.As for comparisons with previous literatures, for all the Δn/=0 transitions,the present RMBPT radiative rates are in agreements with Aggarwal2012 and Nahar1999 within 1.5%and 3%,respectively.

Fig.2.Comparisons of other radiative rates with present RMBPT ones for(a) E1 transitions and (b) forbidden transitions (M1, M2, and E2).Here,other radiative rates are from present MCDHF/RCI calculations, and those of El-Maaref2016,[24] Aggarwal2012,[8] and Nahar1999.[28,38]

We also make comparisons with other theoretical results for E1 transitions.For example,all the current RMBPT radiative rates are in agreements with the MCDHF results for transitions below the 3d level as reported by Denget al.[6]to within 0.5%.Additionally, our RMBPT ones agree with the manybody perturbation theory results for transitions below the 3s level as reported by Johnsonet al.[52]to within 0.3%.Furthermore, the current radiative rates agree with the MCDHF results for transitions below the 4s level as reported by Fischer and Tachiev in the NIST multiconfiguration Hartree-Fock and multiconfiguration Dirac-Hartree-Fock database to within 0.6%.For the sake of simplicity, the comparison with the above three are not plotted in the figure.

However,the newly reported fully relativistic GRASP2K results for all the 130 E1 radiative rates betweenn ≤6 levels from El-Maaref2016[24]have significant deviations with all the other theoretical values and present RMBPT ones, as can be seen from Fig.2(a).For example, compared to our RMBPT results, there are 48, 33, and 21 radiative rates with deviations greater than 5%,10%,and 20%,respectively.The largest difference corresponds to the 2p1/2-6s1/2and 2p3/2-6s1/2transitions,with differences even reaching about a factor of 3.Among the 21 transitions with differences greater than 20%,except for the 5s1/2-5p1/2transition,which is a Δn=0 transition(the difference is from the wavelength),all the other 20 transitions are the Δn/=0 transitions,for which the differences come from the line strengths.It is worth noting that,besides the considerable deviation of transitions involving high levels(n=5,6),there are also significant discrepancies in the radiative transition rates between low levels.For instance,for the 2p1/2-4s1/2and 2p3/2-4s1/2transitions,the radiative rates differences with the MCDHF ones from Fischer and Tachiev in the NIST database are in the range of 22%-24%.In contrast,the present RMBPT values for both the transitions are in agreements with the NIST database ones to within 0.5%.The main reason for such large discrepancies of El-Maaref2016[24]is maybe due to the inclusion of limited (and arbitrary) CI in their work, as explained by Aggarwal[53]for resolving similar issues caused by El-Maarefet al.for sulfur-like scandium,where the deviations of the lifetimes from El-Maarefet al.are up to three orders of magnitude.

As far as forbidden(M1,M2,and E2)transitions are concerned, to the best of our knowledge, the only available theoretical data are from GRASP0 results of Aggarwal2012 for transitions betweenn ≤5 levels.In Fig.2(b), we compare our RMBPT forbidden radiation rates with the results of Aggarwal2012 and observe a good agreement between the two.For strong M1 transitions(i.e.,those greater than 1/104of the maximum radiative rate of the type),most of them are within 1%agreements,and the worst is within 12%agreement,corresponding to the 2p1/2-5p1/2transition.All of strong M2 transitions have less than 1%differences,and most strong E2 transitions also exhibit less than 1% differences.However, there are fourn=2 ton=5 strong E2 transitions having differences ranging from 2%to 3%,with the 2p1/2-5p3/2transition showing the largest difference of 6%.

In Fig.3, we further investigate the impact of configuration interaction (CI) on radiative rates by comparing the results obtained from the three CI modes (RCI1, RCI2, and RCI3) with our present RMBPT results.Interestingly, the RCI1 results, which do not consider any CI, closely match our RMBPT results, with differences mostly within 2% and all within 5%.However, once the CI betweenn ≤6 levels is included(i.e.,RCI2),significant discrepancies are observed for certain transitions.For example,out of 127 strong E1 transitions(i.e.,those greater than 1/104of the maximum radiative rate of the type),30,14,and 7 have differences exceeding 5%,10%, and 20%, respectively, and all of the 7 transitions involven=6 levels.The largest discrepancies are observed for the 2p1/2-6s1/2and 2p3/2-6s1/2transitions, with differences of 57% and 48%, respectively.This suggests that the lifetime of the 6s1/2level could be significantly affected by the CI effect, as these two transitions are important channels for its radiative decay.In fact, the CI effect causes a change in the lifetime of the level by more than 20%,as discussed later in Subsection 3.3.However, when larger-scale CI betweenn ≤8 levels is considered(i.e.,RCI3),the agreements with our RMBPT results immediately improve as expected.The number of transitions with differences exceeding 5%, 10%, and 20% decreases to 16, 7, and 2, respectively.The agreements for the two transitions(2p1/2-6s1/2and 2p3/2-6s1/2)with the largest differences also improve to within 25% and 21%, respectively.An interesting phenomenon worth mentioning is that the radiative rates obtained from our RCI1, which does not consider any configuration interaction,are actually closer to our final RMBPT results compared to our RCI2 involving a small amount of configuration interaction, however, when we further expand the scale of configuration interaction in RCI3, the radiative rates demonstrate closer agreement with our final RMBPT results.This oscillating convergence pattern of atomic parameters as expanding configuration interaction, has also been reported in previous literatures.[51,54,55]This suggests the fortuitous agreements between our RCI1 and RMBPT results are merely coincidental,and that the scale of configuration interaction in our RCI2 is still relatively limited.Therefore, further expansion of the configuration interaction,as demonstrated in the RCI3, is necessary.Finally, based on the RCI3, we consider even more extensive configuration interaction(up ton=200)using the second-order perturbation method leading to our present RMBPT results.

For forbidden transitions, the role of configuration interaction (or correlation) is even more crucial.The RCI1 radiative rates and the present RMBPT ones show good agreements,with strong transitions differing by no more than 10%,and all by no more than 27%.However, the RCI2, which considers configuration interaction between levels withn ≤6, can result in notable differences,particularly for some strong forbidden transitions,around 10%strong forbidden ones with differences larger than 15%(nearly all of them involvingn=6 levels,a few of them involvingn=5 levels),and with differences of up to a factor of four for 2p1/2-6p3/2transition (E2).On the other hand,the RCI3,which takes into account more configuration interaction effects between levels withn ≤8, generally agrees well (within 5%) with present RMBPT results for strong M1 and M2 transitions, with only a few involvingn=6 levels exhibiting radiative rate differences of about 20%,and the majority of strong E2 transitions agree with present RMBPT ones to within 15%,while some transitions with differences greater than 15% involve then=6 levels, with the largest reaching up to 43%for the 2p1/2-6p3/2transition.

Through above detailed comparisons, it is evident that the present RMBPT calculations offer highly precise radiative rates.Strong E1 transition rates betweenn ≤5 levels are typically accurate within 1%, and within 2%for those involving then=6 levels.For strong forbidden transitions,RMBPT radiative rates for most M1 and M2 transition rates are likely to be better than 5%,and 15%for most E2 ones.

3.3.Lifetimes

By utilizing the present RMBPT radiative rates listed in Table 2, one can calculate the radiative lifetime of an excited level using the expression:τj=1/∑i Ai j, here,idenotes all the lower levels that can be accessed from the excited levelj.In the calculations of present RMBPT lifetimes, we consider all the electric dipole allowed transitions (E1) radiative rates, as well as the other forbidden transitions, which include magnetic dipole M1, electric quadrupole E2, and magnetic quadrupole M2 transitions.In fact, our further studies show that the influence of forbidden transitions on the lifetime values of the lowest 35 levels of the iron ion is negligible (less than 0.4%).This can be understood, because each excited level has at least one dominant E1 transition channel connected to it, so considering only E1 transition can obtain accurate lifetime values here for lithium-like iron, although the forbidden ones are required for plasma modelling.[8]

Table 3 presents the lifetimes from both the RMBPT and MCDHF/RCI methods for the lowest 35 levels from then=2-6 configurations of lithium-like iron,including for the ground level 1s22s, the lifetime of which is considered to be infinite.Since our studies mentioned above have shown that the forbidden transitions have negligible contributions for the lifetime values of the ion, the corresponding lifetimes from the present MCDHF/RCI calculation only consider the contributions of E1 transitions,while ignoring the forbidden ones.Additionally, the table also provides the fully relativistic lifetimes from both El-Maaref2016[24]and Aggarwal2012,[8]as well as the quasi-relativistic Breit-PauliR-matrix results from Nahar1999.[28]Furthermore,for the sake of intuitive presentation,we also plot the ratios of various theoretical lifetime values between present fully relativistic RMBPT ones in Fig.4.

As can be seen from Table 3 and Fig.4(a), the present MCDHF/RCI lifetime values match very well with our RMBPT ones,for example,the differences of 21 and 33 lifetime values out of a total of 35 are within 0.2% and 0.4%,respectively,and all the lifetime values differences are within 0.8%.In addition, the present RMBPT lifetimes also match well with those from both Aggarwal2012 and Nahar1999,for example, most of the lifetime value differences are within 0.5%,and all within 1.4%.

In addition, we can also easily see from Table 3 and Fig.4(a)that there are significant lifetime differences between El-Maaref2016 and our RMBPT results(and hence the present MCDHF/RCI ones).For example,among the 30 lifetime values from El-Maaref2016,20,13,10,and 6 of them differ from our RMBPT results by more than 2%,5%,10%,and 20%,respectively.Furthermore, for the 1s24f5/2and 1s26s1/2levels,the differences are even greater than one order of the magnitude.On the contrary,our RMBPT results for these two levels are consistent with those of both the present MCDHF/RCI and Nahar1999, with differences of less than 0.8%.Additionally,we note in the present study that there are no lifetime values for the four levels 6f7/2, 6g9/2, 6h9/2, and 6h11/2in the “Table 3” from El-Maaref2016.Furthermore, the “Table 3” also contains some minor printing errors, such as thejvalue of the second 4d level should be 5/2 instead of 3/2, and thejvalue of the second 4f level should be 7/2 instead of 5/2.Additionally, the lifetime value given by Aggarwal2012 for the 5g9/2level in the “Table 3” should be 7.070×10-13instead of 7.700×10-13.

Such differences of El-Maaref2016 are too large for such a simple three-electrons lithium atomic system.While we have no specific information regarding El-Maaref’s numerical calculations and the subsequent processing of lifetime values for the ion, we highly encourage El-Maaref and other researchers to delve deeper into the ion’s theoretical and/or experimental aspects.While generating atomic data has become more accessible,the accuracy and reliability of such data can be difficult to ensure.Multiple sets of data may be available in literatures,however,not all the users may have the expertises to evaluate the quality of published data.Thus, it is important for data producers to conduct rigorous checks and comparisons to assess the accuracies.While recent data may be assumed to be the most accurate ones,this may not always be the case, as noted by Aggarwal.[56]Hence, atomic data users must exercise discretion and cautions to avoid erroneous conclusions.

We further investigate configuration interaction (CI) effects on the lifetime values of the ion using the relativistic configuration interaction(RCI)method as implemented in the FAC program.[39]We consider three different configuration interaction modes as mentioned above,denoted as RCI1,RCI2,and RCI3,respectively,and the lifetimes from the three modes are also shown in Table 3 and Fig.4(b).

As we consider CI between more and more levels, we expect that the accuracy of the lifetimes would gradually improve from RCI1 to RCI3, but oscillatory convergence might occur, and the subsequent analysis also confirm this type of convergence of the lifetimes.From Fig.4(b), we can see that most of the lifetime values from the RCI1 agree with the present RMBPT ones within 2%, and all within 5%.Such agreements are considered to be a coincidence, because we have not yet considered any configuration interaction between then ≤6 levels.Once we consider these interactions,namely the RCI2 mode, the results immediately become worse, as shown in Fig.4(b), there are many lifetime values that deviate from the present RMBPT values by more than 5%,and the largest deviation corresponding to the 6s1/2level,the deviation even up to 21%,which is quite surprising,because the lithiumlike ion system is simply with only one electron outside the 1s2closed shell,and the nuclear chargeZhere is highly up to 26, but the effect of configuration interaction on the lifetime values is still significant.

Table 3.The lifetime values(τ,in unit s)of lithium-like iron.The table includes our sets of fully relativistic lifetime values and previously theoretical results. τRCI1, τRCI2, and τRCI3 in the table represent lifetime values obtained using three different relativistic configuration interaction modes, where RCI1 and RCI2 represent the calculations without and with considering configuration interaction between the(1s2)nl(n ≤6)levels,respectively,while RCI3 represents the consideration of configuration interaction between more levels with n ≤8.In addition,τRMBPT and τMCDHF/RCI represent lifetime values obtained from our RMBPT and MCDHF/RCI methods, respectively.The τEl-Maaref2016, τAggarwal2012, and τNahar1999 represent lifetime values given in the literature by El-Maaref2016,[24] Aggarwal2012,[8] and Nahar1999,[28,38] respectively, where the Nahar1999 results are quasi-relativistic and the other two are fully relativistic ones.And a±b ≡a×10±b.

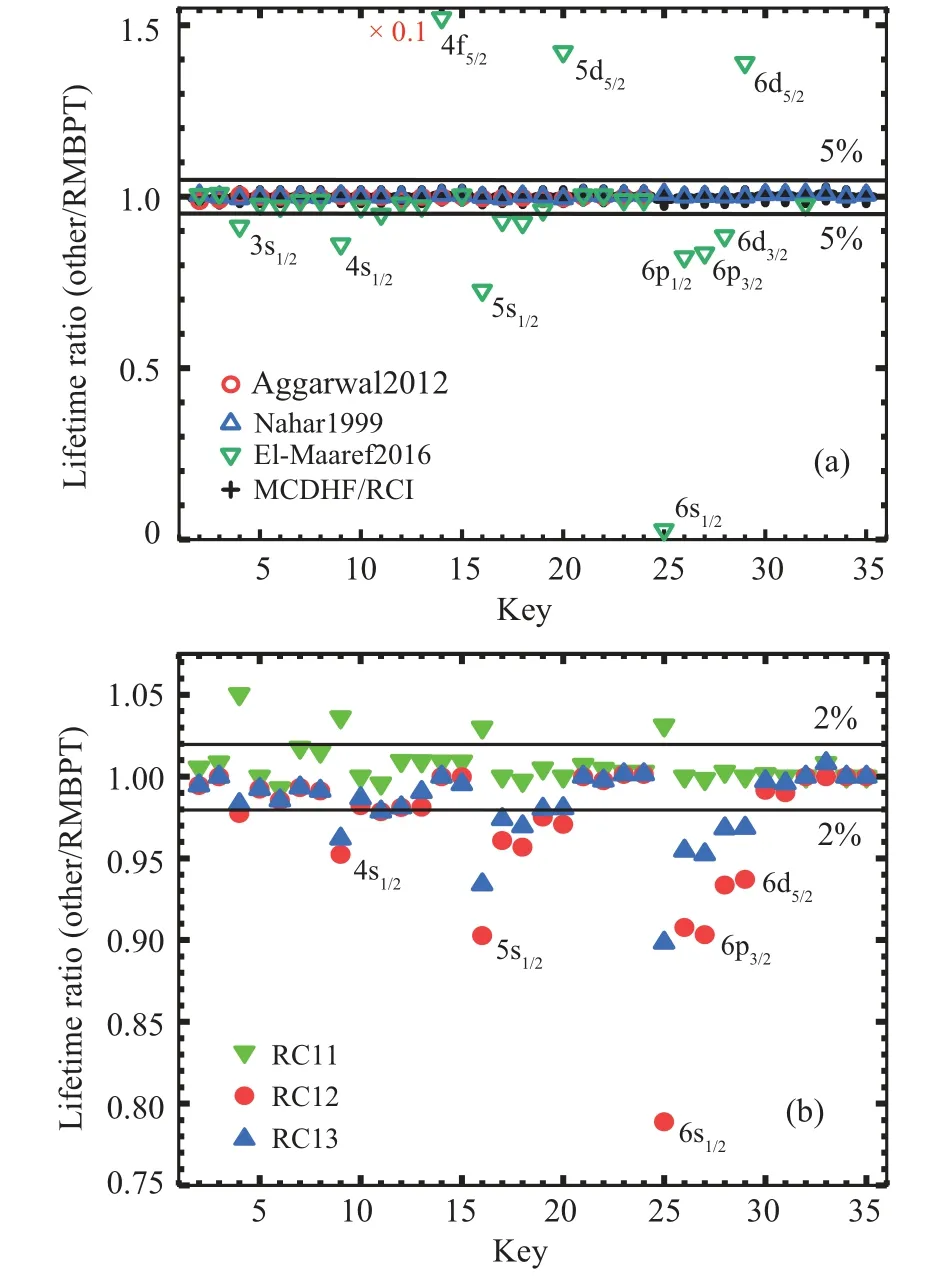
Fig.4.Comparisons of various theoretical lifetime values of Li-like iron with the present fully relativistic RMBPT ones.Panel (a) presents the comparisons between previous theoretical results (i.e., Aggarwal2012,[8]Nahar1999,[28,38]and El-Maaref2016[24])and the present RMBPT ones.To make the results in panel (a) clearer, the lifetime ratio of the 4f5/2 level with Key =14 from El-Maaref2016 is multiplied by a factor of 0.1 (denoted as ×0.1 nearing the 4f5/2 level label).Panel (b) shows the ratios of the results obtained from three different relativistic configuration interaction(RCI) modes (RCI1, RCI2, and RCI3) and also from our MCDHF/RCI to the present RMBPT ones, here, RCI1 and RCI2 represent the calculations without and with considering configuration interaction between the(1s2)nl(n ≤6)levels,respectively,while RCI3 represents the consideration of configuration interaction between more levels with n ≤8.

We continue to consider more configuration interactions,i.e.,considering the interactions between levels withn ≤8.We denote the lifetime values obtained under this mode as RCI3.As shown in Fig.4(b), the RCI3, which considers more configuration interactions, can indeed significantly improve the lifetime values.For example, for the lifetime value of 6s1/2level, it can be corrected by up to about 10%.Our test calculations show that the convergence of the RCI method based on a single central potential for all configurations[39]is very slow.Hence, it is not feasible to achieve even higher precision solely through the pure RCI method.Therefore, based on the RCI3,here,we adopt the second-order many-body perturbation method to incorporate extensive CI correlations withnup to 200 (i.e.our final RMBPT ones), leading to further improvements of the lifetimes by up to about 10%, as can be clearly seen from Fig.4(b).

Finally, the accuracies of the present lifetimes obtained using the RMBPT method, which have been successfully applied in our investigations of highly accurate atomic data for N-like,[41]O-like,[42]and F-like[43]ions, have been demonstrated above through their consistency with our MCDHF/RCI results and previous theoretical ones.[8,28]And configuration interaction effects are important for the calculations of lifetime values of the ion.

4.Conclusion

Using the fully relativistic RMBPT method, we have provided energies and lifetime values for the lowest 35 energy levels from the 1s2nlconfigurations(wheren=2-6 andl=0,...,n-1)of lithium-like iron Fe XXIV,as well as complete data on the transition wavelengths, radiative rates, absorption oscillator strengths, and line strengths between the levels.The transitions include both allowed (E1) and forbidden(magnetic dipole M1,magnetic quadrupole M2,and electric quadrupole E2)ones.Our level energy precision is within 0.05%,and the radiative rate accuracy of strong E1 transitions withinn ≤5 levels is within 1%, and for transitions involving then=6 levels, it is within 2%.For strong forbidden transitions,the current RMBPT radiative rates for M1 and M2 transitions have accuracies likely better than 5%, while most E2 transitions have accuracies better than 15%.Secondly,we have found that configuration interaction is crucial for lithiumlike ions.To obtain accurate energies and radiation data for the ion, careful consideration of configuration interaction is required.Our present RMBPT results have potential applications in the identification of spectral lines,as well as in plasma modeling and diagnosing.

Acknowledgments

Project supported by the Research Foundation for Higher Level Talents of West Anhui University (Grant No.WGKQ2021005).The author (S Li) also would like to express his gratitude for the support received through the Visiting Researcher Programs at Fudan University (C Y Chen’s research group)and the Institute of Applied Physics and Computational Mathematics (J Yan’s research group).The authors would also like to express their gratitude to Y R Zhu for many valuable discussions in this research.The authors sincerely thank the referee and the editor for their thorough review and valuable comments on this manuscript,their feedback has greatly benefited our work.