介孔吸附常用经典分析模型的比较

张伟庆，胡谷平

中山大学化学学院，广州 510275

相对于用分子动力学方法如非定域密度函数理论(NLDFT)、计算机模拟方法(GCMC)分析材料物理吸附数据的现代分析方法，笔者以为在分析中凡是用到BET方程[1]、Kelvin方程[2]4,5(上标4,5代表页码，下同)或Kiselev方程[3]、多孔固体表面上膜厚度[4]、层数[5]127,128与压力关系的或用到标准等温线[4]的方法都可以称为经典介孔分析方法。这些分析方法要比NLDFT和GCMC易于理解，只需具备高中数学及微积分初步知识和大学普通物理知识即可掌握，因此经典介孔分析方法早已被人们广泛使用。而目前NLDFT、GCMC还在发展中。

20世纪50年代至今，已发展了多种经典介孔分析方法，其中一些已被仪器公司开发成商业化软件而获得应用。这些商业化软件中有模型及选项设置，但如何选用或恰当设置选项是仪器用户和研究人员在实验过程中需要自行解决的问题。本文简要介绍了经典介孔分析方法的发展历史、应用范围和各自特点，期望对读者有所助益。

限于篇幅，本文未涉及常见的选吸附支或选脱附支用于分析及迟滞和假峰现象。

1 对介孔吸附常用经典分析方法的基本认识

Wheeler[5]158将BET多层吸附理论和Kelvin方程结合，提出吸附量是由多层吸附和毛细管凝聚两部分构成的观点。这一观点被人们普遍接受，并体现在后续发展的经典介孔分析方法中。

1.1 对孔、模型等基本术语的界定

孔分为开孔和闭孔，闭孔不属于吸附研究的范畴。对孔进一步分类并定义如下[2]2,3。

盲孔(blind pore)：末端封闭的孔(dead-end pore)，与外表面只有1路连接的开孔。

开孔(open pore)：与外表面相连的空腔或通道，可理解为与外表面有1路或多于1路连接。

墨水瓶孔(ink bottle pore)：颈部窄的开孔。

内连孔(interconnected pore)：与一个或多个其他孔相连的孔。

通孔(through pore)：完全穿过样品的孔，可理解为与外表面至少有2路连接。

由上述对孔的定义可知，盲孔、墨水瓶孔、内连孔和通孔都属于开孔。有的文献提及“开孔”时没有特别明确是“盲孔”或“通孔”，如“开口圆柱孔”，应是指圆柱状通孔。实际上，无论“盲孔”还是“通孔”，在分析时若选脱附支则其结果一般不受影响[6]。另外，在有的分析方法[3]中还提及一个与孔(pores)相近的词——芯(cores)，被定义为孔隙中空的部分，其壁上含有吸附膜。

另外，在本文中当侧重于原理、理论介绍时称为“模型”，如“BJH模型”[7]；当侧重于将“模型”应用于分析数据时则称为“方法”，如“BJH方法”。而“无模型法”[3]、“完全无模型法”[8]则是针对孔的假设形状而言的。

1.2 介孔分析中的数学关系式

介孔分析用到的数学关系式如BET方程、Kelvin方程和膜厚度、层数以及BJH方法计算等已有文献详细介绍，在此不再赘述[1],[2]1-16,[7-11]。在经典介孔分析方法中还会用到Kiselev方程和水力半径计算公式[3]，其含义如下：

Kiselev推导了毛细管凝聚的一般热力学方程，即：γds=Δμda，式中，γ是液体吸附物的表面张力；ds是孔隙被毛细管凝聚填充时消失的表面积；Δμ是气体凝聚前后化学势的变化；da是孔隙吸收的液体物质的量。可证明，Kelvin方程是前述一般热力学方程的一个特例，适用于圆柱形毛细管。Kiselev成功地使用该方法测定了许多具有宽孔的吸附剂的比表面积，所获得的比表面积与BET比表面积非常一致[3]。

Kiselev方程适用于吸附或脱附等温线的滞后区域即多层吸附和毛细管凝聚同时发生的区域。在无模型方法提出之前，确定孔隙体积和孔隙表面分布的所有方法都基于圆柱或平行板孔隙形状模型；水力半径计算公式没有假设孔隙的形状，所得的孔隙体积和孔隙表面积分布不是作为从圆柱或平行板孔隙的Kelvin方程获得的半径的函数确定的[3]，而是作为水力半径(rh)的函数。孔或一组孔的水力半径定义为：rh=V/S，其中，V是孔或一组孔的孔体积；S是孔隙壁的表面积。于是，可用水力半径作为一组孔的平均宽度的量度。该定义适用于任何形状的孔，对于圆柱状孔，rh等于圆柱半径的二分之一；对于平行板孔，rh是两平行板之间距离的二分之一[3]。

1.3 介孔吸附常用经典分析方法比较

将介孔吸附常用经典分析方法及相关知识按时间顺序列成表1，并将方法适用孔型、孔径范围、样品种类、与BET比表面积数值上的关系和方法特点扼要列出，以方便了解、对比。

表1 有关经典介孔分析方法发展历程及相关知识

2 对介孔吸附常用经典分析方法的分类

可将表1所列的方法分成四类：有模型法、无模型法、完全无模型法和逆向法。

2.1 有模型法

有模型法包含平行板状孔和圆柱状孔两类孔型。各种有模型法之间有其相通之处，可从已被列为“标准”[2]1-16的BJH模型着手，掌握该模型后再结合其他各自模型和方法的特点，即可较完整了解有模型法。表1中的BJH方法、Pierce方法、Montarnal方法、CI方法、DH方法、Roberts方法、Broekhoff方程、Faas方法、近似Broekhoff方法和简化Broekhoff-de Boer方法均属于有模型法。

每个有模型法都有其特有的假定、适用范围和分析步骤，现以BJH模型为例介绍其要点：

“标准”对BJH模型[2]15有三条假定：(1) 孔隙是刚性的，并具有规则的形状(比如圆柱状或平行板状)；(2) 不存在微孔；(3) 孔径分布不连续，超出方法所能测定的最大孔隙即在最高相对压力处，所有测定的孔隙均已被充满。

该模型的计算[2]15需采取三个步骤：(1) 数据点均按压力降低的顺序排列；(2) 将压力降低时氮气吸附体积的变化归于两方面的贡献：毛细管凝聚物的脱除和孔壁上多层吸附膜的减薄；(3) 为准确计算孔径和孔体积，必须考虑毛细管凝聚物从孔隙中脱除时会残留多层吸附膜。

该模型计算的难点是如何确定上述“两方面贡献”的比例。详细计算过程可参考相关文献[2]15-17和资料[11]。

2.2 无模型法

Brunauer等人提出了无需假定孔形状的孔分布计算方法即无模型法[27]。

该方法有三个特点：(1) 使用水力半径；(2) 使用比Kelvin方程更一般的Kiselev方程来计算表面积变化；(3) 计算得到的是芯(cores)分布。如要获得孔径分布时需假定孔模型。

目前只了解到一种无模型法，已在表1中标明。严继民等人[5]177-183对“无模型法”进行了详细分析和整理，指出它并非是严格的“无模型”法。还将包括“无模型法”和以前那些假设圆柱状孔、平行板型孔的、似乎相互关系不大或根本无关的方法中的各个独立的公式归纳成为一个数学通式，使它们各自成为某种条件下该通式的特例[5]158-162,277-285,[33]。

2.3 完全无模型法

孔分布计算包括两部分即毛细管凝聚和多层吸附。有学者[8,35]认为：多层吸附可用标准等温线表示，毛细管凝聚部分可由实测等温线与标准等温线之差表示，由此提出了新的孔分布计算法。此法无需指定孔的形状，或许由于先前的“无模型法”被认为并不是真正的无模型法，该方法被称为“完全无模型法”。

完全无模型法有三个特点[35]：(1) 增量取吸附层数而不是通常方法中的孔半径；(2) 引入恒定的BET比表面积值；(3) 从低压向高压计算(与BJH方法的计算顺序相反)，计算起点是吸附等温线的V-n图与标准等温线V-n图发生偏离的那一点，其中V是吸附量、n是吸附层数。

该方法可能有二点不足[35]：(1) 与其他方法一样，Kelvin方程是否能够真正表征多孔固体中的毛细管凝聚现象是存有疑问的；(2) 当样品同时发生毛细管凝聚和微孔充满现象时，两者可能相互抵消，而使V-n作图仍为直线或毛细管凝聚量减小时，计算可能带来错误信息。如个别二氧化硅样品的计算结果与其他方法计算结果有很大差别，就可能是由于这种情况引起的。

2.4 逆向法

基于经典方法，并人为地在经典方法的方程一侧增加一个附加项，使其得到的表观数据与其他仪器分析结果的数据相符，称这类方法为“逆向法”。表1中列出近年人们发展的4种“逆向法”，即原始BJH-KJS方法、改进BJH-KJS方法、PM方法和VBS方法。

逆向法完全是为了使吸附分析结果与其他仪器分析结果表观值相符且限于特定样品的方法，有兴趣和需要的读者可查阅相关文献。对该类方法，除了知道适用哪些条件外，对其算式无需过多解读。逆向法在分析中也都先指定模型，有着与有模型法形式相近的数学表达式，但因其逆向引入了新参数或附加项，与完全依靠推导得来的有模型法的数学表达式存在着本质上的不同。

逆向法由于有其他分析仪器测试数据的支持，其指定模型(孔形状)时的依据是比较充分的。

逆向法有着实用、简单的优点，随着电镜、粉末衍射等其他仪器参与到多孔材料特别是有序介孔材料的表征中，今后逆向法的数学表达算式或许还会不断增加。

2.5 对假设孔型的认识

孔分析中有三种等效孔型可供选择：狭缝型(或平行板型)、圆柱状孔和球型孔。

选这三种孔型的原因是[5]156：(1) 平行板型孔的两个主曲率都等于零，球型孔的两个主曲率都等于同一圆曲率，平行板型孔与球型孔代表了两种极端情况；(2) 圆柱状孔的两个主曲率一为零、一为某一圆曲率、介于平行板型孔和球型孔两者之间，圆柱状孔是统计最优的，实际分析中最常用的模型是圆柱状孔，其次是平行板型孔。

应注意到，前面所讨论的有模型法在选孔型时很少涉及球型孔，微孔分析中有球型孔选项，而在介孔分析中没有，其原因或许与吸附机理有关：微孔吸附遵从填充机理，孔或是全充满或是全空；介孔吸附遵从凝聚机理，吸附凝聚是逐步进行的，假设有属于介孔研究范围的球型孔，其孔壁不可能是完全密闭的，其壁上必有介孔尺寸大小窗口与外界连通，则这个孔就同“墨水瓶孔”[5]112,122,[12]134-147,[41]一样了，这可能是早期介孔分析中很少涉及到球型孔的原因。不过，随着有序介孔材料(如SBA-16等)的出现，现在已对介孔球型孔包括“墨水瓶孔”有了许多新的认识[20]292-294,545,546,[37,39,40]。

3 常见分析软件中的选项及设置

挑选了较常用的三家仪器公司配套分析软件(分别称为软件A、软件B和软件C)，将其分析方法列成表2，并对BET方法共有选项及BJH方法特有选项做了说明。

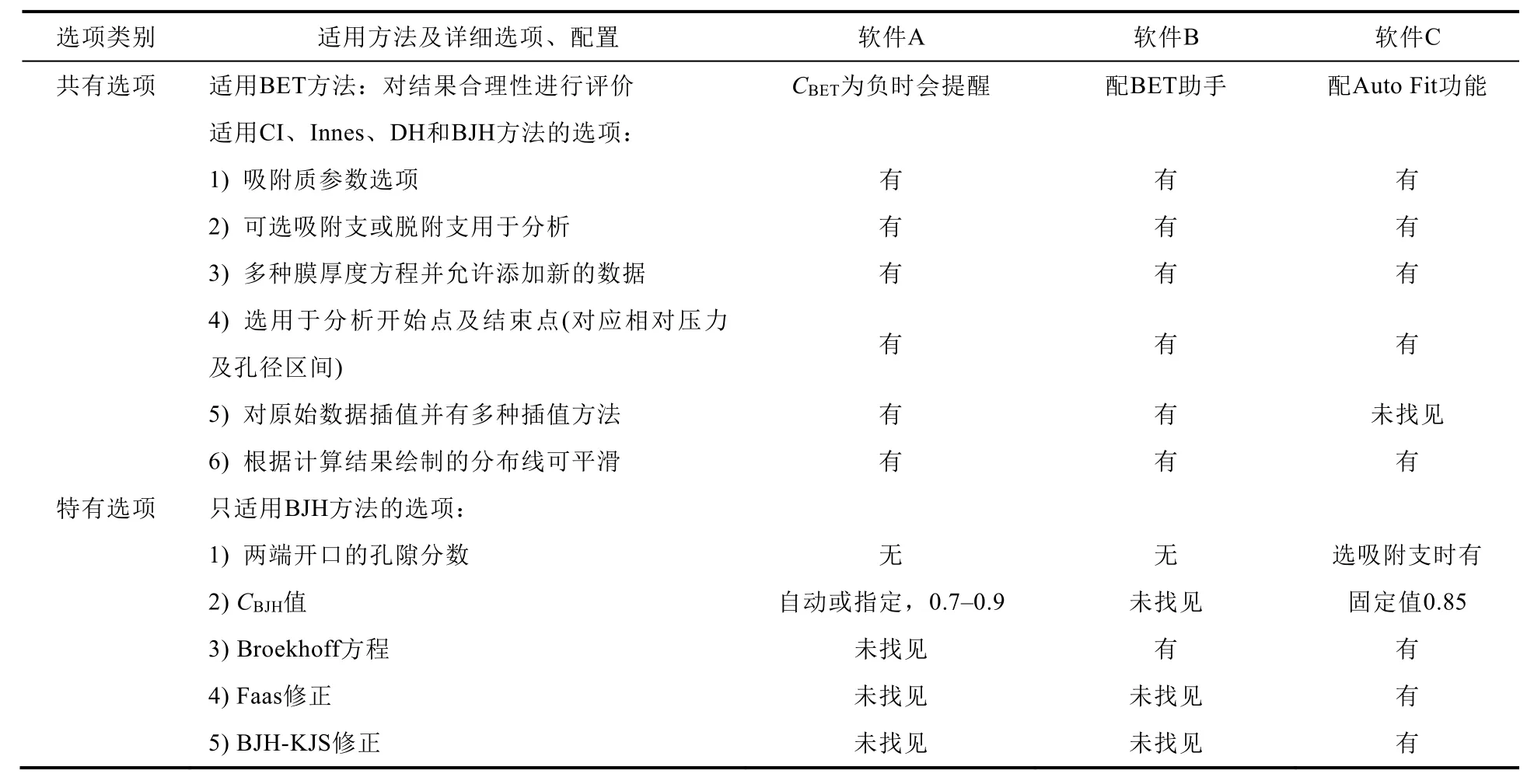
表2 不同仪器公司配套软件分析方法选项配置对比

3.1 BET数据合理性评价

由于人们常用BET比表面积值与相应方法的孔壁累积比表面积值之间的一致性[28]来评价介孔分析方法，因此，BET模型在介孔分析中有特别重要的地位。目前，BET模型和方法[1]已成为了“标准”[42]，建立了筛选数据规则[43]，仪器公司在各自软件中陆续开发了诸如“BET助手”和“AutoFit”等辅助功能。然而，由于新型多孔材料不断涌现、仪器测试性能不断提高，测试所得数据按标准和规则筛选后剩余的数据点仍很多且都是在“规则”允许的拟合范围内，以致有时选拟合范围内不同点所计算的BET比表面积值仍有很大差别。由此可知，即使有仪器软件帮助，若欲得到合适的BET比表面积值仍不是一件简单的事情。

最近，有学者对BET测试数据选点问题[44]进行了深入研究，开发了一种新的BET分析工具即BETSI软件[45]，据称该软件能够选择出一个最佳拟合区域，可以最大程度地降低计算误差。

3.2 BJH方法特有选项

同一模型在不同公司的分析软件中其设置选项往往不同，如有的公司的BJH方法软件中有一些特有选项，在各自手册中有简略介绍，为完整理解BJH方法，再补充说明如下：

(1) 对两端开口的孔隙分数值的设定：设为0时对应一端开口的盲孔，设为1时对应两端开口的通孔，还可依据样品孔的情况尝试设定0与1之间的数值。

(2) 对CBJH选项的归纳和认识：CBJH并不是一个常数，而是BJH模型中一个与孔径有关的变量。Barrett等人[7]考虑到孔径与p/p0的对应关系，得出了CBJH数值随p/p0变化的趋势：当p/p0越来越小直至趋近于0时，CBJH则会越来越大直至趋近于1；当CBJH值的变化在±0.05范围内时，对计算的孔隙体积分布的影响几乎可以忽略不计。为了简化计算，有的分析软件固定CBJH= 0.85；有的分析软件则提供了自动计算或手动输入(限0.70、0.75、0.80、0.85和0.90)的选择。

(3) Broekhoff方程修正：在软件中有两处用到此选项(液膜厚度和体积)。可根据修正方程适用范围及样品实际情况选用。

(4) Faas修正：该修正较少使用，在仪器手册中相关内容也很少，需要时请研读文献[34]。

(5) BJH-KJS修正：在软件中有两处用到此选项(液膜厚度和体积)。BJH-KJS修正有原始方法和改进方法两种，从文献[34]中所列BJH-KJS修正算式推断软件使用的是原始BJH-KJS方法。可根据修正方程适用范围及样品实际情况选用。

若所选用的分析软件中没有自己需要的共有选项或特有选项，可以参照相应文献介绍的方法，直接利用原始吸附数据和相应方法进行计算。

另外，Sonwane等人[46]提出一种能同时确定微孔和介孔材料孔径分布的新方法，成功地预测了纯MCM-41和二元MCM-41物理混合物的孔径分布，根据所测数据分析，其结果和NLDFT获得的孔径和与通过XRD获得的实际孔径都很接近。有学者从更广阔的视角对目前微孔、介孔吸附数据分析中的缺陷与局限性进行了系统评述[47]，其观点被广泛认可。

经典模型对分析吸附数据非常有用，但只适用于给定的等温线部分，只能部分地处理比较复杂的材料，这些模型目前存在的主要局限性是未考虑网络效应，对孔隙和孔壁的几何效应和能量效应的描述也不充分，因此需要进一步完善。

4 结语

对常用经典介孔分析方法的相关知识、方法分类及其特点、适用范围等进行了简要介绍和比较，同时对其存在的不足进行了讨论；对BET数据的合理性分析有助于深刻理解其他介孔分析方法的特点和适用性；对3种常用介孔分析软件的选项与设置进行了比较，为使用者提供了建议。随着介孔或混合孔材料的发展，这些分析方法和软件亦可能获得迭代更新，因此研究人员需要对这一领域保持持续的关注。

致谢：拙稿在返修过程中得到陈六平教授的悉心指导，特此致谢！