两组分理想液体混合物的温度组成曲线单调性的证明

雷艳华，邓斌

湘南学院化学与环境工程学院，湖南 郴州 423000

蒸馏是分离均相液体混合物的典型单元操作，是化工生产中最重要分离方法之一。它是通过加热形成气液两相体系，利用体系中各组分挥发度的差异使其中组分得以分离[1]。在一般的物理化学、化工原理等课程中往往都有专门的章节介绍。蒸馏的原理一般从两组分理想液体混合物的定义出发，通过拉乌尔定律、道尔顿分压定律等进行数学推导得到气液平衡相图以及泡点方程、露点方程等等。在气液平衡的温度组成(T-x)图中，教材中往往都会指出[2]：气相线以及液相线是单调上升或者单调下降曲线；只有当液体是非理想液体混合物时，它们才会出现极大值或者极小值，形成共沸物。这句话只是作为结论给出，但没有任何教材给出严格的数学证明。本文将给出理想液体混合物的T-x曲线是单调曲线的严格证明。

1 泡点方程与露点方程

对于A、B两种液体组成的理想液体混合物，每一种物质的分压都遵守拉乌尔定律。从而可以得到液相摩尔分数与总压以及饱和蒸气压的关系：

上式中p表示气相总压，pA*、pB*分别表示两种液体的饱和蒸气压，xA、xB则分别表示两种物质在液相中的摩尔分数(下面的yA、yB则分别表示两种物质在气相中的摩尔分数)。液体B在不同温度下的饱和蒸气压可以用克劳修斯-克拉珀龙方程(简称为克-克方程)的不定积分式或者定积分式表示[3]：

式中ΔvapHm,B表示B液体的摩尔蒸发焓，R是气体常数，C是不定积分常数，TB*是纯B液体在标准大气压下(pӨ)的沸点。一般的化工原理教材里面，都是用一个经验方程给出饱和蒸气压与温度的关系。最常见的方程为安托因(Antoine)方程[4]：

安托因方程中的C、D以及E对每一种物质都是一个常数，但是不同的物质则有不同的数值。安托因方程与克-克方程相比，主要区别是在分母中的温度加上了一个常数。我们后面将说明克-克方程以及安托因方程将给出同样的结论，因此我们先以克-克方程为例进行证明。由于T-x图是保持总压p为一个常数，我们先假设总压强为标准大气压。别的压强条件下，只是公式中引入一个压强的比值，不影响结论。将(4)式代入(2)式，即可得到沸点温度与液相组成的函数关系，即液相线的方程，也可称为泡点方程。

我们可以得到xB与T的函数关系如式(6)所示，但我们没法得到T与xB的函数关系。但根据导数之间的关系，dy/dx= 1/(dx/dy)，因此(∂T/∂xB)p与(∂xB/∂T)p两者具有相同的正负性。由道尔顿分压定律以及气相摩尔分数yB的定义，我们可以给出yB与xB以及温度T的函数关系，即气相线的方程，也可称为露点方程。

为得到T与xB(或yB)的单调关系，我们必须得到它们的导数，由(6)式或者(7)式直接求导，有较大的难度。我们采用另一种方法给出它们的导数关系。

2 单调性的证明

2.1 泡点方程单调性的证明

对于描述系统状态的三个变量之间的偏微分应该满足如下关系[5]：

而两组分气液平衡系统可通过T、p、x、y等变量描述。因此，T、p、x三个变量的偏微分满足如下关系：

通过(9)式，可将T与xB的偏微分转为另两个容易求导的偏微分的乘积。由(1)式可得：

总压与温度的导数可以从克-克方程得到。克-克方程的微分形式为：

它的变形表达式为：

由此我们可以得到摩尔分数不变的情况下，总压与温度的偏导数为：

结合(9)、(10)以及(13)式，我们得到

公式(14)中分母项中的变量均为正值。如果混合物在沸点温度范围内，一种物质的饱和蒸气压总是大于另一种物质的饱和蒸气压，则沸点随组成变化的单调性得到证明。那么能否满足一种物质的饱和蒸气压始终大于另一种物质的饱和蒸气压呢？我们以下面一节专门讨论一下。

2.2 不同物质饱和蒸气压的大小的讨论

由于液体的饱和蒸气压满足克劳修斯-克拉珀龙方程，即lnp*与1/T成直线关系，如果两种物质的摩尔蒸发焓相等，则一种物质的饱和蒸气压始终高于另一种物质的饱和蒸气压。由于理想液体混合物的分子体积相等，分子间作用力也相等[2]，因此可认为理想液体混合物摩尔蒸发焓相等。从而上面2.1节关于温度组成的单调性得到证明。但真实液体混合物基本不可能摩尔蒸发焓完全相等，却仍然有不少液体混合物的温度组成曲线是单调的，我们将进一步做出说明。原则上只要两种物质的摩尔蒸发焓不相等，即两条直线的斜率不相等，则两条直线必然存在一交点。在交点处，两者的饱和蒸气压相等，如果在交点以前，物质A的饱和蒸气压更大的话，则在交点之后，物质B的饱和蒸气压更大。但是由于真实的液体存在临界温度等原因，真实的液体不一定存在交点。如图1(A)所示，列出了四种醇类同系物(甲醇、乙醇、正丙醇以及正丁醇)从273 K至接近各自临界温度的饱和蒸气压的实验点[6]以及用克劳修斯-克劳珀龙方程拟合的结果。在各自的临界点温度之下，四条直线是没有交点的。但是如果假设四条直线可无限延伸的话，如图中虚线所示，则彼此都有交点。这是虚拟的交点，但我们也可以找到两种具有真实交点的物质。如图1(B)所示，列出了六种物质在不同温度下的饱和蒸气压，除了上面的四种醇以外，还加上了丙醛和丙酮两种物质。将丙醛与四种醇比较，在430 K以下，丙醛的饱和蒸气压都比四种醇的饱和蒸气压大。高于430 K时，甲醇的饱和蒸气压开始大于丙醛的饱和蒸气压。同样，甲醇和乙醇在约380 K和460 K超过丙酮的饱和蒸气压。

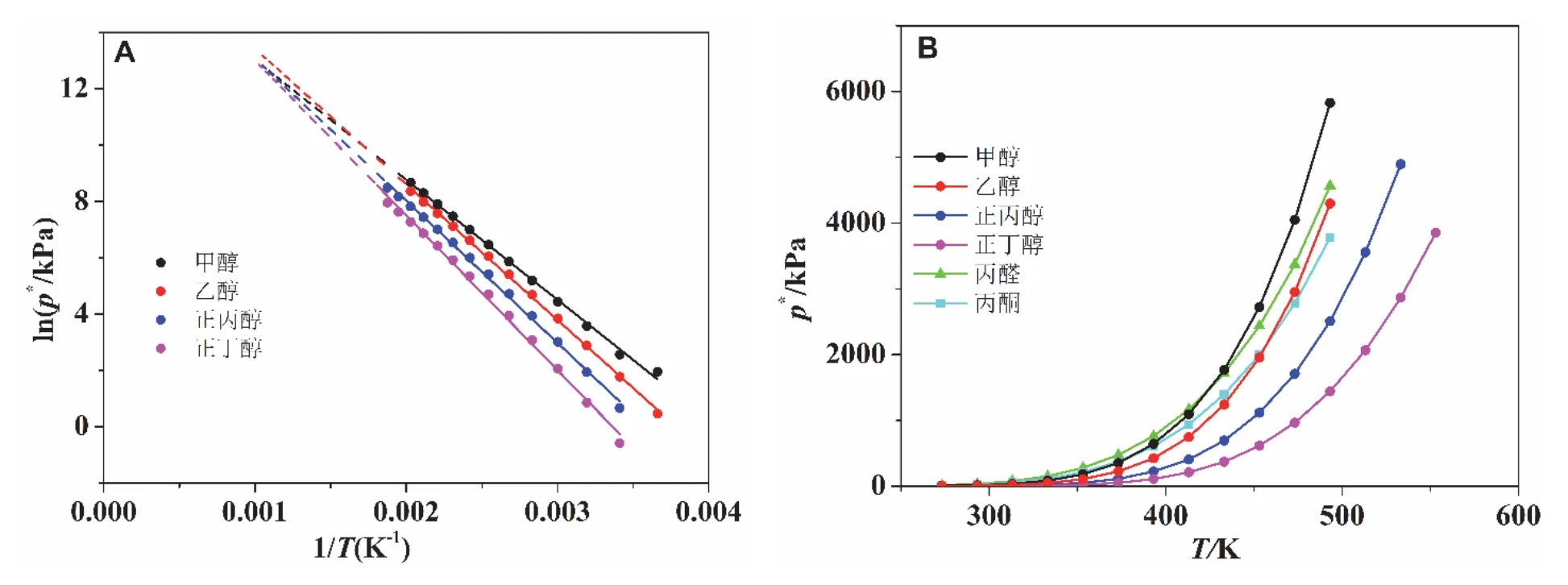
图1 几种物质的饱和蒸气压与温度的关系曲线

以甲醇和丙醛两种物质为例，根据拟合的克劳修斯-克拉珀龙方程，两种物质的饱和蒸气压在温度为432.85 K时相等，数值为1715.277 kPa。在p-xB图上(设B为丙醛)，温度为432.85 K时的p-xB为一条水平线。温度低于432.85 K时，丙醛的饱和蒸气压更高，由公式(1)，p-xB是向上的直线；高于432.85 K时，甲醇的饱和蒸气压更高，p-xB是向下的直线，如图2所示。由于T-xB图都是在某一个固定的压强下得到的。如果压强保持为一大于1715.277 kPa的数值，该压强只可能与下降型直线相交，则T-xB图上的沸点范围必然高于432.85 K。压强保持为一小于1715.277 kPa的数值，情况刚好反过来。两种情况都可以保证其中一种物质的饱和蒸气压在沸点范围始终大于另一种物质的饱和蒸气压。因此仍然可以保证在2.1节所需要的条件，在研究范围内，一种物质的饱和蒸气压大于另一种物质的饱和蒸气压，从而可以得到T-x曲线的单调性。

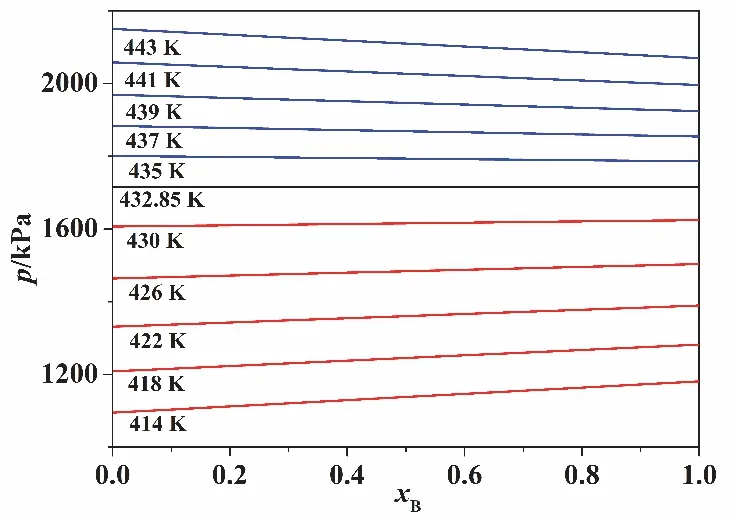
图2 甲醇与丙醛在交点温度以及附近温度的总蒸气压-组成曲线

我们也特别强调一点，如果压强正好在1715.277 kPa，此时从理想液体混合物定义来看，则混合物的沸点将不随组成的变化而变化。这个现象或结论在我们的知识范围内还没有任何研究人员指出。温度越接近432.85 K，p-xB的关系直线越接近水平直线，这有助于我们在实验上观察到混合物的沸点不随组成的变化而变化。

2.3 露点方程单调性的证明

要得到沸点温度T与气相组成yB的导数关系，我们可以从如下基本关系出发：

在总压不变的情况下，两边分别微分，并对温度做偏导数得到：

右边第一项可由(14)式求出，第二项必须进一步计算。由微分运算法则，我们可以得到：

由于液体的饱和蒸气压只是随温度而改变，不会随着组成的变化而变化。因此，

将(12)、(14)以及(19)式代入(17)式，得到：

比较(14)式与(21)式，我们可以得到结论，(∂T/∂xB)p与(∂T/∂yB)p具有相同的单调性。在沸点组成图上，液相线是单调下降曲线的话，则气相线也是单调下降曲线。

3 关于安托因方程的讨论

前面是假设液体的饱和蒸气压遵守的是克-克方程，如果液体饱和蒸气压遵守的是安托因方程，此时公式(11)变为：

相应地将公式(14)、(20)、(21)中的ΔvapHm,A/(RT2)换为DA/(T+EA)2，ΔvapHm,B/(RT2)换为DB/(T+EB)2。由公式(22)可以看出，如果温度升高，物质的饱和蒸气压变大，则常数D的取值为正，此时温度与气相摩尔分数或者液相摩尔分数的偏导数都与相应的克-克方程下的偏导数具有相同的单调性。事实上，只要能保证随着温度的升高，液体饱和蒸汽压变大，则任意函数都具有相同的单调性。当然，如果某种物质能发生温度升高，液体的饱和蒸气压反而变小的情况(或者在克-克方程中出现液体的摩尔蒸发焓为负值的情况，即液体变为气体反而放热的情形)，则理想液体的T-x图上也会有极大或者极小值。虽然这种情况在实验中还未发现，我们仍然指出这种情况。

4 结语

我们按照函数偏微分的关系，将两组分理想液体混合物液相线的温度与组成的偏微商表示为两个容易求导的偏微分，从而可以证明当液体温度升高饱和蒸气压变大，且其中一种组分的饱和蒸气压总是大于另一种组分的饱和蒸气压，则液体混合物的液相线温度随着一种物质液相组成的增加而单调变化。而后通过气相摩尔分数与液相摩尔分数间的关系，证明了气相线与液相线具有相同的单调性。最后我们讨论了饱和蒸气压是遵守安托因方程还是克-克方程对结果的影响。