大跨度钢混组合梁斜拉桥黏滞阻尼器减震研究
2023-11-01石小林郭伦波
石小林 郭伦波
(中铁二院工程集团有限责任公司 成都 610000)
桥梁工程作为重要的生命线工程,通过适当的方式减小地震对桥梁的作用,确保桥梁在地震作用下的结构安全十分重要。目前采用的桥梁减隔震技术主要有2种:①通过设置隔震支座,延长结构周期,使结构自振周期避开地震反应卓越周期段,从而减小结构的地震响应;②通过设置地震耗能装置,增加结构阻尼,以耗散地震能量,从而达到减震目的[1-2]。
对于一般的漂浮和半漂浮体系斜拉桥,其结构的刚度一般较小,自振周期较长,结构阻尼小[3]。因此,通过增大结构周期的方式,其隔震效果多不理想。对于这类长周期结构,更多采用的是增大结构阻尼的方式来耗能减震。
黏滞阻尼器作为一种被动减震控制装置,主要依靠黏弹性材料的滞回耗能特性,为结构提供附加刚度和阻尼,减小结构的动力反应,从而达到减震目的[4]。我国自1999年开始,将黏滞阻尼器应用于江阴长江大桥,以控制结构振动产生的位移[5]。近年来,黏滞阻尼器因其安装方便、造价较低、减震效果好等优点在桥梁减震领域应用越来越广泛,而合理地选择阻尼系数和阻尼指数是黏滞阻尼器发挥作用的关键[6-8]。
本文以某大跨度组合式混合梁斜拉桥为工程背景,对其黏滞阻尼器进行参数敏感性分析,通过对比在不同阻尼系数和阻尼指数下的纵向减震效果以确定该桥黏滞阻尼器的最佳设计参数。
1 工程背景
某“混凝土-组合梁”组合式混合梁斜拉桥桥梁总体布置见图1。
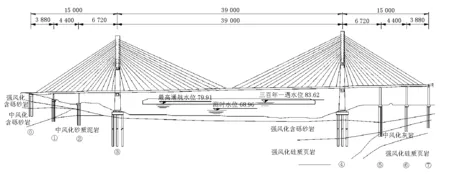
图1 总体布置图(单位:尺寸,cm;高程,m)
主跨布置为150 m+390 m+150 m,主跨为钢混组合梁,边跨主梁为预应力混凝土“π”形梁,主塔采用钢筋混凝土H形塔,基础为承台桩基础。边跨分别设2个辅助墩,布置辅助墩后边跨跨径组成为38.8 m+44 m+67.2 m。边跨和中跨典型断面见图2、图3。
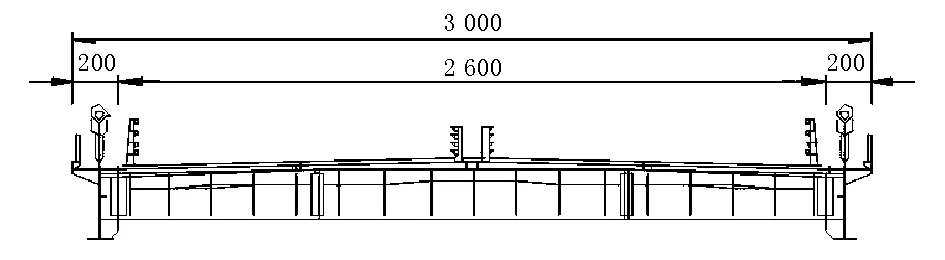
图2 中跨钢-混凝土组合梁断面图(单位:cm)
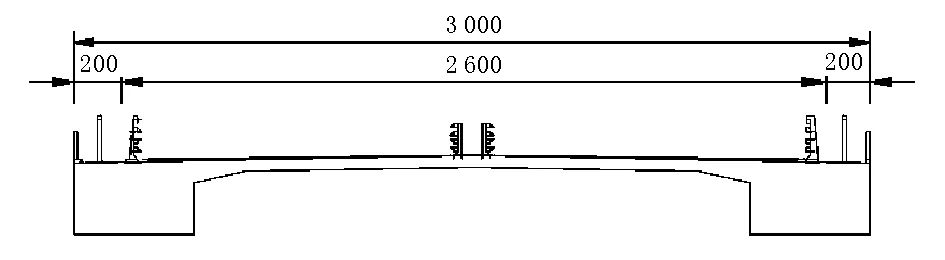
图3 边跨混凝土“π”形梁断面图(单位:cm)
桥梁为半漂浮体系,在3号、4号主塔处设置双向活动竖向球钢支座。为控制结构的纵桥向地震响应,在2个主塔的塔梁间分别设置2对黏滞阻尼器。桥梁的支承约束体系见图4。

图4 支承约束体系布置图
2 有限元模型建立
采用midas Civil 2021程序并基于“鱼骨模型”建立桥梁地震分析有限元模型,其中梁体和主塔采用梁单元模拟,拉索采用桁架单元模拟。桩-土作用采用表征土介质弹性值的m参数计算的等代“土弹簧”模拟,结构阻尼采用瑞利阻尼,阻尼比取0.03。结构计算有限元模型见图5。桥梁的基频为0.136,自振周期为7.34 s。 第一阶振型为纵漂,桥梁为长周期结构。

图5 有限元模型
3 地震波选取
根据GB 183006-2015 《中国地震动参数区划图》、GB 50011- 2010 《建筑抗震设规范》(2016 年版),桥梁设计基本地震加速度为0.1g,地震反应谱特征周期0.35 s,测区抗震设防烈度为VII度。JTG/T 3365-01-2020 《公路斜拉桥设计规范》规定:斜拉桥E2地震作用宜采用100年超越概率4%的地震动。根据地震安全性评价,地表场地水平向地震动参数见表1(阻尼比0.03),竖向场地地震动峰值加速度按水平向峰值加速度的100%取值。

表1 工程场地地表水平向场地地震动参数
地震安评单位以地震危险性分析得到的基岩加速度峰值和反应谱作为目标函数,用三角级数迭加方法合成了3条地震波,见图6。本文以这3条地震波作为设计地震动输入模型。
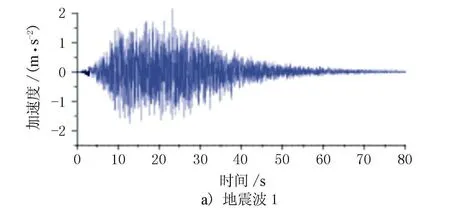
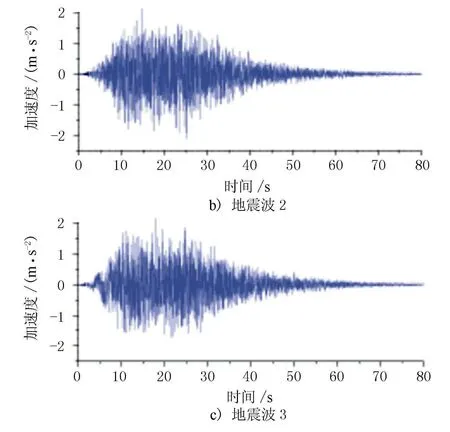
图6 人工拟合地震波
4 黏滞阻尼器力学参数分析
黏滞阻尼器(FD)可采用midas Civil自带的Maxwell模型进行分析,Maxwell模型见图7。
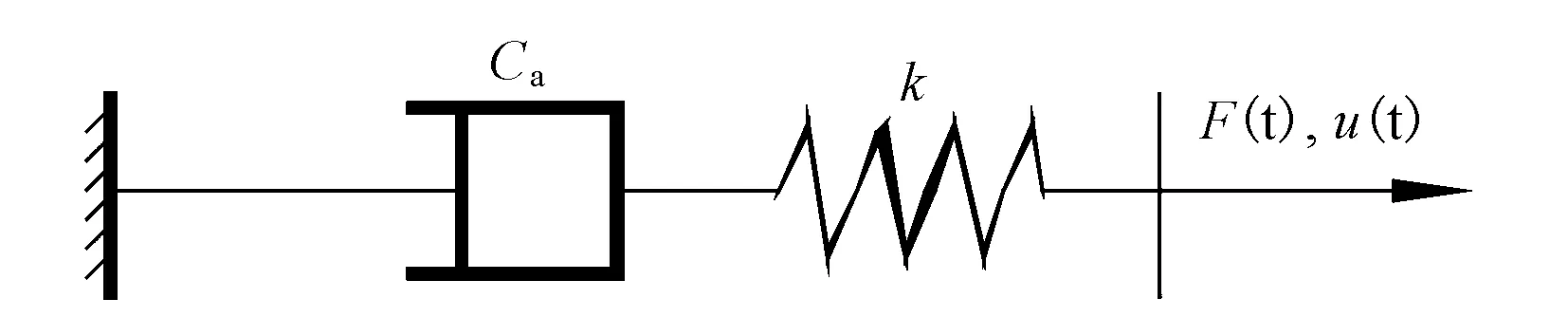
图7 Maxwell数学物理模型
其恢复力表达式为
Fd(t)=kdk=C·|v|α·sgn(v)
(1)
式中 :Fd(t)为黏滞阻尼器产生的阻尼力;k为串联弹簧的刚度(本文取×10-6);dk为弹簧变形量;C为阻尼系数;α为阻尼(速度)指数;v为相对运动速度(本文取1 m/s);sgn(·)为符号函数,当v>0时,sgn(v)=1;当v=0时,sgn(v)=0;当v<0时,sgn(v)=-1。
黏滞阻尼器的力学参数包括:阻尼系数、阻尼指数、设计位移,以及设计最大阻尼力。
4.1 阻尼系数和阻尼指数敏感性分析
阻尼系数和阻尼指数是黏滞阻尼器最主要的2个力学参数。本文以主塔塔底纵向弯矩、剪力,以及主梁梁端位移为控制指标,研究阻尼系数和阻尼指数的不同取值对结构的影响。阻尼指数取值一般为0.2~1.0[9],本文取0.2,0.3,0.4,0.5,0.6;阻尼系数分别取1 500,2 000,2 500,3 000,3 500,4 000,4 500,5 000 kN·s/m。
图8~图10分别为基于有限元模型计算的塔底弯矩、塔底剪力、梁端位移与阻尼系数的关系曲线。分析图8~图10可知,阻尼器对主塔减震效果显著,设置阻尼器后,主塔内力和主梁位移明显减小。桥塔弯矩减小幅值为27.3%~57.6%;桥塔剪力减小幅值为18.3%~38.9%;梁端位移减小幅值为36.7%~83.1%。如图8所示,墩底弯矩随着阻尼系数C的增加而减小,随着阻尼指数α的增大而增大。桥塔弯矩曲线没有最小值,但当C>3 000 kN·s/m时,曲线趋于平缓,阻尼器对弯矩的减小效果减弱。
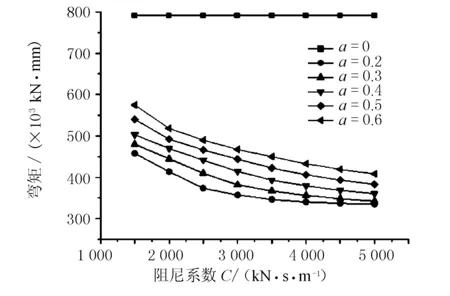
图8 塔底弯矩与阻尼系数的关系曲线
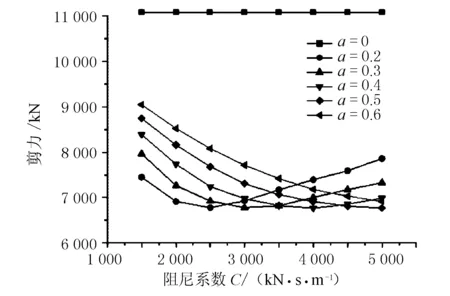
图9 塔底剪力与阻尼系数的关系曲线
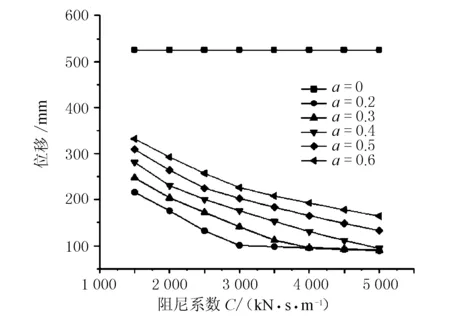
图10 梁端位移与阻尼系数的关系曲线
如图9所示,塔底剪力曲线总体趋势是随着阻尼系数C的增加而减小,并且在α=0.2、C=3 500,α=0.3、C=3 000,α=0.4、C=4 000时取得最小值。当C<3 500 kN·s/m时,塔底剪力随着C的减小而减小;当C≥3 500 kN·s/m,α≤0.4时,塔底剪力随着α的减小而呈缓慢增加趋势。
如图10所示,梁端位移总体随着C增大而减小,随着α的减小而减小。当C<3 500 kN·s/m时,位移减小趋势较大;C≥3 500 kN·s/m时,位移减小趋势变缓。当α=0.2,C≥3 500 kN·s/m时,梁端位移减小幅值趋近于0。
综合上述分析,当C>3 500 kN·s/m、α<0.3时,阻尼器对结构的的减震作用变小。同时,进一步增大阻尼器的C和α,阻尼器的减震效果增加较小而制造阻尼器的成本增加较大。因此,将C=3 500 kN·s/m、α=0.3作为本项目的阻尼器设计参数。
4.2 设计位移
黏滞阻尼器的设计位移是保证其正常使用的必要条件。阻尼器的位移主要有抗震位移、风振位移。阻尼器的设计位移取值取决于2个方面:①在静力工况下,需确保阻尼器能适应结构的正常变形,包括恒载和活载引起的位移;②在地震工况下,需确保阻尼器能满足减震耗能的位移行程。地震工况下的位移一般取:1.2×地震作用+0.5×温度作用。静力工况和地震工况的位移计算结果见表2。
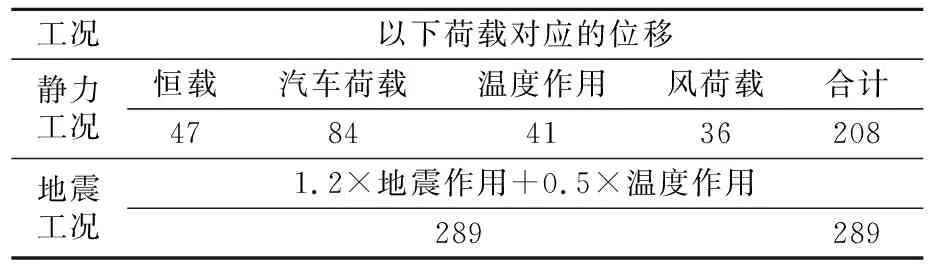
表2 梁端位移计算值 mm
因此,考虑一定的富余,将黏滞阻尼器设计位移取为±300 mm可以满足要求。
4.3 设计最大阻尼力
设计最大阻尼力是黏滞阻尼器在正常工作状态下可产生的最大输出力。在确定阻尼系数C、阻尼指数α、相对运动速度v3个参数后,阻尼力可根据式(1)求出。在C=3 500 kN·s/m时,取不同的α、v的阻尼力曲线见图11。
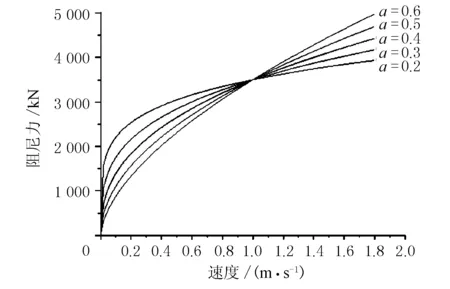
图11 阻尼力与速度的关系曲线
由图11可见,当v<1.0时,α越小,阻尼力越大;而当v>1.0时则相反,α越小,阻尼力也越小。
图12为阻尼器在不同C及α下的输出力。可以看出,阻尼力随着C增大而增大,随着α的增大而增大,符合图11所示规律。在C=3 500 kN·s/m、α=0.3时,F=2 287 kN,考虑一定的富余度,将阻尼器的设计最大阻尼力确定为2 500 kN。
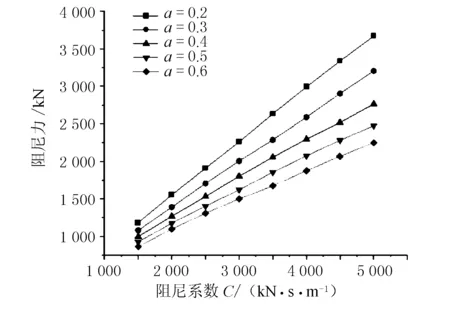
图12 阻尼力随阻尼参数的变化曲线
5 减震效果分析
从黏滞阻尼器的减震效能角度出发,以过渡墩与梁相对位移、塔顶位移、塔底纵桥向弯矩,以及塔底剪力为量化指标,通过对比分析设置阻尼器前后桥梁在地震荷载作用下的结构响应情况,证明黏滞阻尼器的减震效果。限于篇幅,本文仅给出3号桥墩在大震50年超越概率2%下1号波的计算结果,结构地震响应情况见图13~图16。
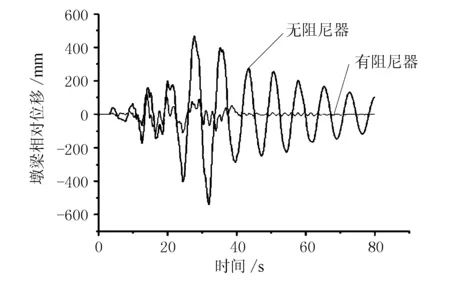
图13 墩梁相对位移时程曲线对比
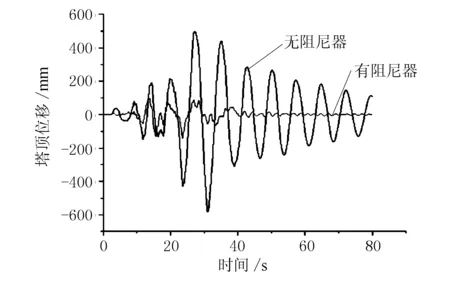
图14 塔顶位移时程曲线对比
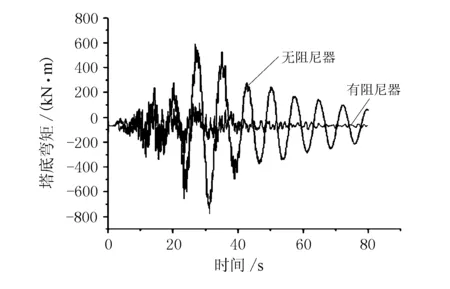
图15 塔底弯矩时程曲线对比
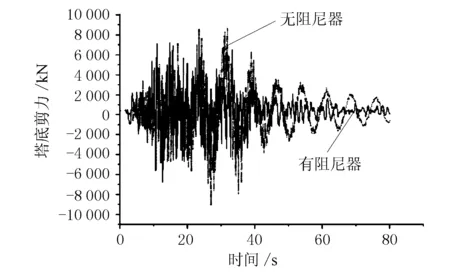
图16 塔底剪力时程曲线对比
由图13~图16可知,安装黏滞阻尼器后,墩梁相对位移和塔顶位移及主塔受力减小明显。墩梁相对位移减小73.7%,塔顶位移减小75.7%,塔底弯矩减小52.7%,塔底剪力减小14.5%。说明黏滞阻尼器有效地吸收了地震能量,减震效果较好。
6 主塔截面弹塑性分析
索塔塔底为矩形空心截面,结构外轮廓尺寸为1 000 cm×700 cm(纵向×横向),壁厚120 cm,混凝土等级为C50。布置双排直径32 mm的HRB500钢筋,间距为15 cm。根据JTG/T 3365-01-2020 《公路斜拉桥设计规范》规定,在E2地震作用下,索塔截面由地震组合产生的弯矩设计值应小于截面等效抗弯屈服弯矩(考虑轴力)。为此,应用UCFyber软件将桥塔截面划分为纤维单元,采用实际的钢筋和混凝土应力-应变关系分别模拟钢筋和混凝土单元,采用数值积分法进行截面N-M-φ(弯矩-曲率)分析(考虑相应的轴力),得到截面的弯矩-曲率曲线。通过弯矩-曲率曲线可以得到截面的等效抗弯屈服弯矩,然后比较E2地震作用下主塔截面最大弯矩与求得的屈服弯矩大小来判断截面是否处于弹性状态。图17~图18分别为截面网格划分和求得的弯矩-曲率曲线。截面屈服弯矩计算结果见表3,在阻尼器的减震作用下,主塔截面处于弹性阶段,满足规范要求。
图17 UCFyber主塔截面网格划分
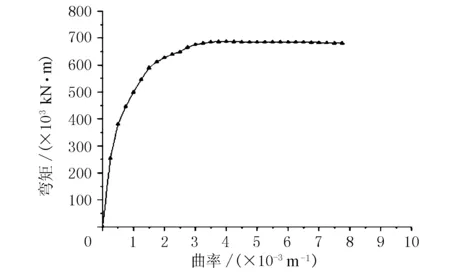
图18 塔底截面弯矩-曲率曲线

表3 主塔截面弯矩值 kN·m
7 结论
本文以某“混凝土-组合梁”组合式混合梁斜拉桥为工程背景,通过对黏滞阻尼器进行参数敏感性分析和桥塔弹塑性分析,得出以下结论。
1) 以主塔塔底纵向弯矩、剪力和主梁梁端位移为评价指标,黏滞阻尼器可以有效控制结构地震响应,减震效果明显。
2) 参数敏感性分析结果表明,当C=3 500 kN·s/m、α=0.3时,黏滞阻尼器对结构的内力和位移控制效果较好。
3) 黏滞阻尼器的设计位移应能满足结构在静力工况下的变形和地震工况下减震耗能行程。可以取静力工况和地震工况位移的较大值并考虑一定的富余度系数。
4) 通过对主塔截面进行弹塑性分析,得到主塔的屈服弯矩。结果表明,安装黏滞阻尼器后的桥梁在E2地震作用下主塔处于弹性状态,结构受力满足规范要求。
