大跨径钢箱梁最大悬臂状态非线性静风稳定性分析*

苗建宝 骆佐龙

(1.西安公路研究院有限公司 西安 710065; 2.山西大学电力与建筑学院 太原 030000)

大跨度连续钢箱梁桥在静风荷载的作用下,可能会发生静风失稳现象[1]。静风失稳包括扭转发散和侧向弯扭屈曲失稳2种形态。扭转发散主要由静力风荷载中的升力矩引起,侧向弯扭屈曲则由阻力导致。从已有的风洞试验结果来看,扭转发散的危险性更强[2]。大跨度连续钢箱梁桥静风稳定性计算的特点须充分考虑结构几何非线性及荷载非线性,材料非线性通常可以忽略不计。已有的静风失稳模型实际上是一种理想化的第一类稳定问题,在力学模型建立方面做出了许多简化处理,如将结构的扭转恢复力非线性模型简化为线性模型;将气动力对攻角的非线性函数关系简化为线性函数关系;将结构弯扭耦合失稳模态简化为单一模态失稳,并且简化后的广义扭转刚度取值并不具有一般性等。随着计算机应用技术的发展,为了提高静风稳定性计算的精度,目前普遍采用建立全桥三维有限元空间模型进行静风稳定性精细化分析,采用有限位移理论或内外增量结合的迭代方法进行求解,可以得到比较满意的结论[3]。但有限元分析理论会随着单元自由度的增加耗费大量的运算时间,并且网格划分精度的不同会导致解的不确定性甚至最终解缺失。因此,需要提出一种改进的静风失稳模型以充分考虑上述问题,以提高静风稳定性分析计算效率和精度从而满足跨海大桥建设的需要。

1 工程简介

1.1 工程概况

港珠澳大桥跨越伶仃洋海域,东接香港,西接珠海和澳门,主体工程全长约29.6 km,是世界上最长的跨海桥梁工程。跨越崖13-1气田管线桥属于港珠澳大桥DB01标段的非通航孔桥,联跨组合为110 m+150 m+110 m,采用小节段预制、大节段装配的施工工艺,最长拼装节段为152.6 m,为国内同类型桥梁之最。主梁采用整幅变截面三跨连续钢箱梁结构,顶板为正交异性钢桥面板结构,宽33.1 m;中墩墩顶两侧各5 m区段梁高为6.5 m,墩顶两侧各37.5 m区段梁高从6.5 m线性变化至4.5 m,其余区段梁高为4.5 m。

跨越崖13-1气田管线桥施工过程在最大悬臂状态时,由于最大悬臂长度较长、结构整体刚度较小,且桥位处设计基准风速较高,因此风荷载对结构处于最大悬臂状态时的稳定性与安全性均产生不利影响,需对结构在最大悬臂状态下的静风稳定性进行分析与评价,以策安全。跨越崖13-1气田管线桥处于最大悬臂状态时的立面及横截面布置图见图1。

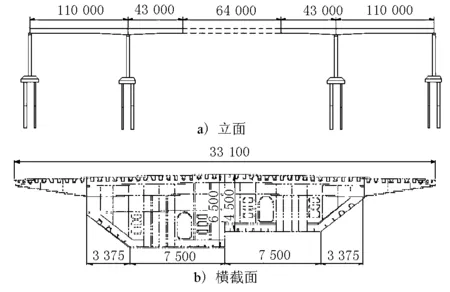
图1 跨越崖13-1气田管线桥最大悬臂状态立面及横截面布置(单位:mm)

1.2 抗风设计参数

跨越崖13-1气田管线桥桥址处冬、夏季风交替明显,为亚热带海洋性季风气候:夏季多受台风影响,易出现暴雨、雷暴天气;冬季多有寒潮、大风降温天气。受热带气旋及季风影响,桥位处常年处于高风速状态影响,设计基准风速较高。结构抗风设计参数取值见表1。

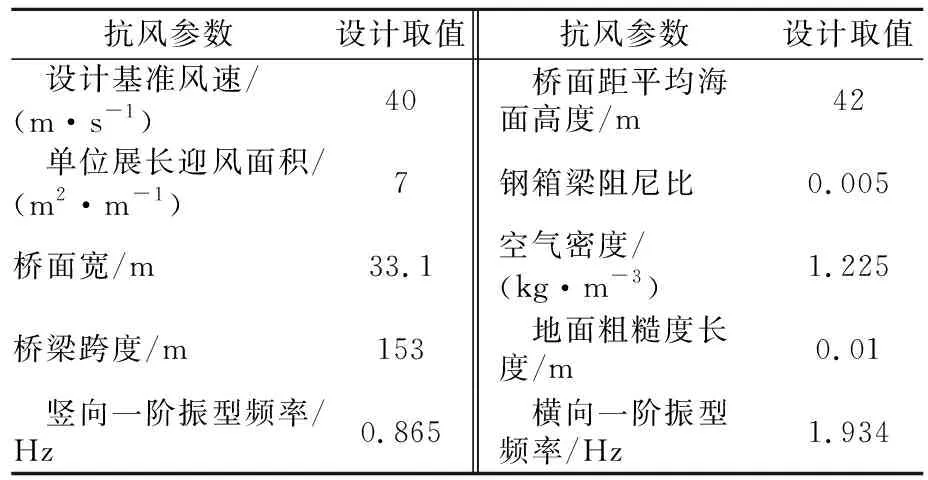
表1 跨越崖13-1气田管线桥抗风设计参数

2 静风效应计算

进行非线性静风稳定性分析,首先需要明确结构各断面的静力三分力系数[4-5]。跨越崖13-1气田管线桥结构形式为变截面连续钢箱梁桥,主梁截面高度桥梁纵向差异较大。理论研究证明,静力三分力系数与主梁截面的宽高比有关[6-8]。因此,主梁纵向不同位置处的截面其静力三风力系数会有一定差异,需要分别进行计算。

静力三分力系数的计算采用有限元数值模拟的方法进行[9-10],以商用CFD软件Fluent为计算平台。计算域尺寸的选取能够保证计算域各个边界距离主梁断面足够远以使主梁断面附近空气流动不受边界条件的影响。网格划分采用自适应网格技术,对主梁横断面风速变化较大的区域增大了网格密度,以降低数值黏性的影响,提高静力三分力系数数值模拟的精度。计算域尺寸及主梁横断面典型网格划分见图2。图中B为主梁宽度,D为主梁高度。

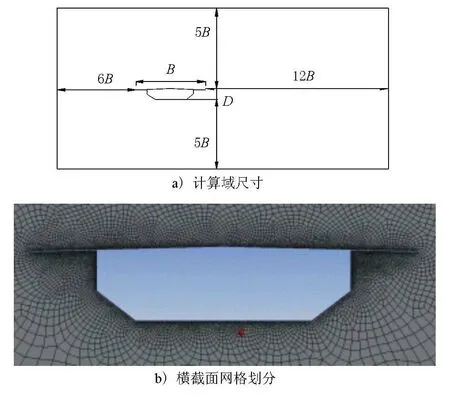
图2 计算域尺寸及主梁横断面典型网格划分示意

根据相关研究,自然风攻角的范围一般为-5～5°,因此需要明确结构静力三分力系数在风攻角为-5°～5°区间范围内相应的数值及变化趋势。主梁墩顶断面在不同风攻角作用下的风场分布图见图3。

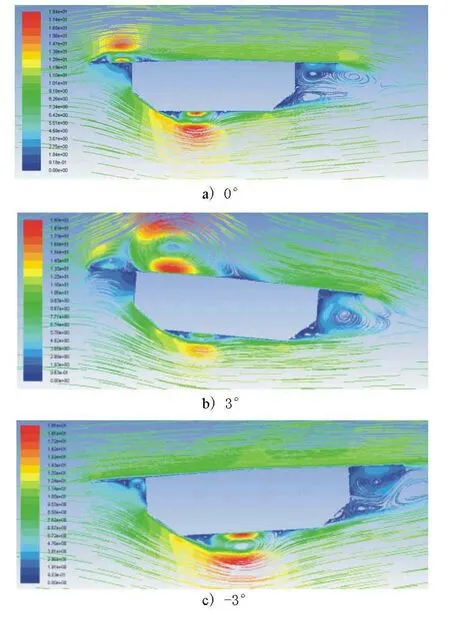
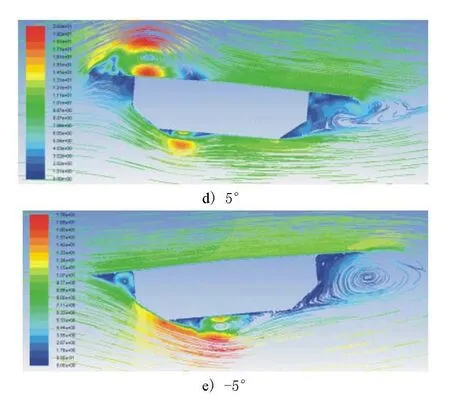
图3 不同风攻角作用下主梁典型断面风场分布示意

根据不同初始风攻角作用下主梁典型断面风场分布分析结果,可以计算出不同初始风攻角作用下主梁典型断面的静力三分力系数见图4,图中PS为支点截面,SS1～SS4为分别距离支点10.5,20.5,30.5,43.0m截面。

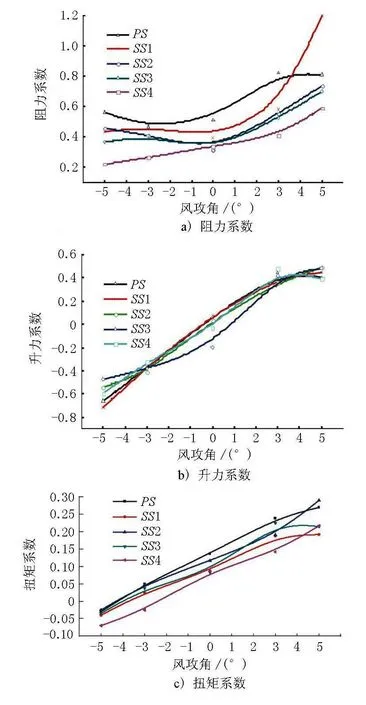
图4 主梁典型断面静力三分力系数

根据以上静力三分力系数计算结果,在风速一定的情况下,选取不同的初始风攻角,进行结构水平、竖向和扭转位移响应的计算。在设计基准风速作用下,主梁不同断面(节点)处的横向位移和扭转角随初始风攻角变化示意见图5。

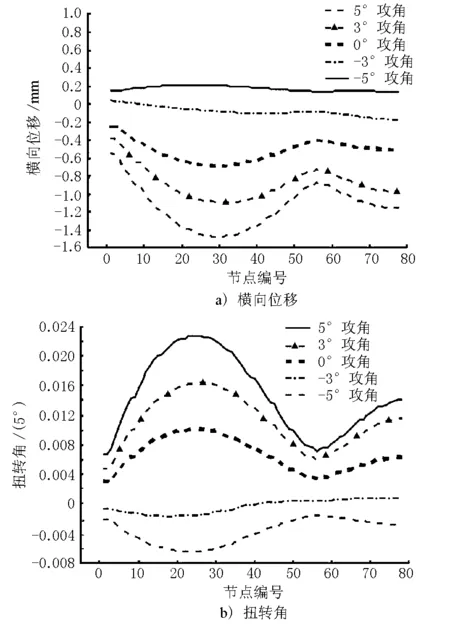
图5 主梁不同断面(节点)处的横向位移和扭转角随初始风攻角变化示意

由图5可知,在正攻角(0°～5°)范围内,主梁横向位移的变化幅度大于负攻角(-5°～0°):正攻角范围内,主梁横向位移最大值为-1.47mm;负攻角范围内主梁横向位移最大值为0.25mm。主梁扭转角也有同样的规律,在正攻角范围内的最大扭转角为0.023°;负攻角范围内的最大扭转角为-0.007°。因此,可以得出在设计基准风速条件下,跨越崖13-1气田管线桥处于最大悬臂状态时,结构整体静风稳定性较好。

跨越崖13-1气田管线桥在主梁合龙之前处于单悬臂状态,由于结构未形成整体,总体刚度偏小,并且桥位处风速较大,结构所处的风场特性复杂,可能处于比设计基准风场更加不利的风场范围内。因此,需要对跨越崖13-1气田管线桥进行静风稳定性分析,以策安全。

3 非线性静风稳定性分析

跨越崖13-1气田管线桥最大悬臂状态非线性静风稳定性分析流程见图6。

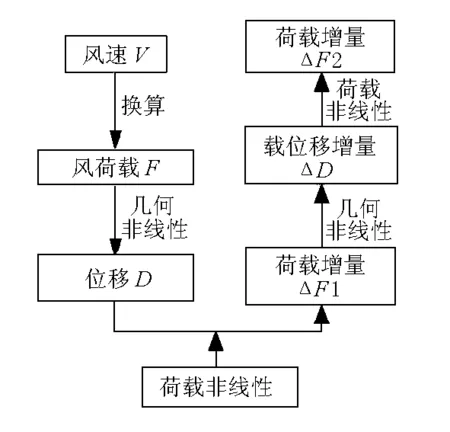
图6 非线性静风稳定性分析流程

选取结构在最大悬臂状态时的边跨跨中截面与悬臂端截面作为非线性静风稳定性分析的2个控制断面,首先由图4计算出2个控制断面的静力三分力系数,由于2个控制断面尺寸接近,以悬臂端截面为典型断面进行静力三分力系数的计算,结果见图7。

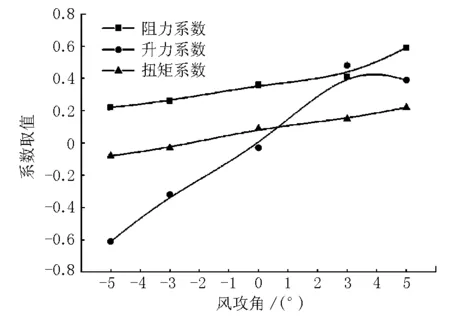
图7 典型断面静力三分力系数

由静力三分力系数求解作用于结构上的静风阻力、升力及扭矩,将其作为外荷载施加于结构控制断面上,采用内外增量双重迭代法并考虑结构几何非线性和风荷载非线性,按照图6所示非线性静风稳定性分析流程,对不同初始风攻角作用时,在不同风速作用下控制断面的扭转角度进行计算。结构在风荷载作用下控制断面的风速-扭转角变化曲线示意(0°攻角)见图8。

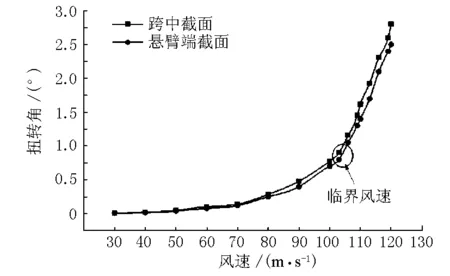
图8 风速-扭转角变化曲线

由图8可知,当静风荷载以0°攻角作用于结构上时,随着风速的提高,结构扭转角具有非线性增长的趋势,当风速为103 m/s以内时,扭转角增长幅度并不明显,曲线的非线性特征并不明显,近似呈线性分布规律;当风速超过103 m/s时,扭转角增长幅度急剧增加,曲线呈现非线性增长趋势,直至结构出现静风失稳现象。因此,通过上述分析可以得到当静风荷载以0°攻角作用于结构上时,结构的扭转发散临界风速为为103 m/s。若以临界风速与设计风速之比作为结构静风稳定系数K,即:

K=vL/v0

(1)

式中:vL为扭转发散临界风速;v0为设计基准风速。

在0°攻角作用下,钢箱梁最大悬臂状态稳定系数为e0=103/40=2.58,则该攻角下结构的稳定性能够得到保证。同理可计算得到初始风攻角为-5°,-3°,3°,5°时,结构扭转发散临界风速与稳定系数,见表2。

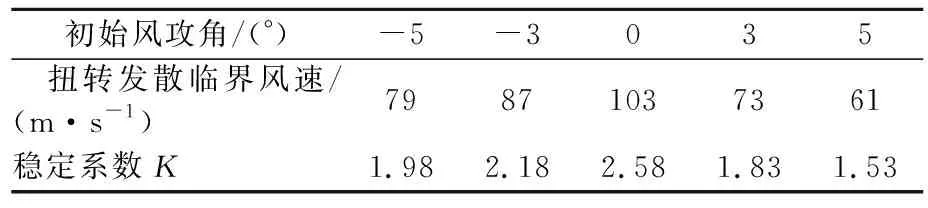
表2 不同初始风攻角对应的临界风速与稳定系数

由表2可知,跨越崖13-1气田管线桥在不同初始风攻角作用下结构的扭转发散临界风速介于61～103 m/s之间,最小值为61 m/s,出现在当初始风攻角为5°的情况下;稳定系数介于1.53～2.58之间,最小值为1.53,同样出现在当初始风攻角为5°的情况下。因此,可以得出跨越崖13-1气田管线桥最大悬臂状态在常规风荷载的作用下,结构的静风稳定性能够保证。同时,负攻角范围内的临界风速值较正攻角范围高,稳定系数也相应较大,据此结论,建议采用导流装置将来风方向尽可能从主梁下缘转移到上缘,以提高结构扭转发散临界风速。

4 结语

1) 通过对大跨径钢箱梁最大悬臂状态非线性静风稳定性的分析,得到在不同初始风攻角作用下结构的扭转发散临界风速为61～103 m/s,因此,可以得出跨越崖13-1气田管线桥最大悬臂状态在常规风荷载的作用下,结构的静风稳定性能够保证。同时,负攻角范围内的临界风速值较正攻角范围高,可以采用导流装置将来风方向尽可能从主梁下缘转移至上缘,以提高结构扭转发散临界风速,确保大桥顺利建设。

2) 在正攻角范围内,主梁横向位移最大值为-1.47 mm;负攻角范围内主梁横向位移最大值为0.25 mm;在正攻角范围内的最大扭转角为0.023°;负攻角范围内的最大扭转角为-0.007°,在不同初始风攻角作用下结构稳定系数介于1.53～2.58之间。因此,可以得出在设计基准风速条件下,跨越崖13-1气田管线桥处于最大悬臂状态时,结构整体静风稳定性较好。