仿生构件碰撞响应的动态子结构方法分析

宋孟军, 魏京功, 魏 坤, 赵海军

(天津职业技术师范大学 汽车与交通学院,天津 300222,E-mail:songmj@tute.edu.cn)

仿生机构以其良好的自然形态,具有优越环境适应能力,一直是引人注目的研究领域,各国学者进行了大量的研究与实践工作,已研制出了多种具有仿生机构的移动机器人,如麻省理工学院的仿生机器人实验室研制的仿生豹机器人奔跑速度可以达到22 km/h,能量利用效率(COT)可以高达52%[1];文献[2]基于猎豹的骨骼肌肉系统,构建了气动四足仿生机构,以合理的肌肉及关节布置,实现了仿生机械腿的快速运动;文献[3]则通过构建整体仿生机,对四足移动机器人的运动性能进行深入研究。然而作为仿生机构的重要组成部分,仿生构件在机器人运动过程中具有重要的作用,为此,研究人员已经展开较为广泛的研究,如为获得良好的弹跳性能,文献[4]通过弹簧、工程塑料等对微型机器人的仿生机械腿进行了构建;为获得机器人稳定的行走运动,文献[5]则通过加入减振垫片以及小型阻尼器等构建对仿人机器人的机械足端进行了构建;然而,机器人足端与地面接触过程通常较难观测与记录,而其接触瞬间所产生碰撞力对机械腿,乃至机器人本体都具有重要的影响,如文献[6]对机器人足地接触过程中,被动行走足端的足地接触的致动机理进行了研究[7];文献[8]则对被动行走机构足地接触点的位移、速度以及接触力等动运动学特性进行了数值计算与仿真研究。由于足地接触瞬间时间极为短暂,仿生机构在接触碰撞瞬间,其动力学响应属于高度非线性问题[9-12],其过程的求解存在许多难点[13], 如撞击力的计算、撞击的发生与分离时间的判断,以及撞击瞬态波传播过程的描述等,且柔性构件系统与刚性构件系统的碰撞问题有着明显的差异。

因此本文,将针对组成仿生机构常用构件的瞬态动力学特性进行分析与研究,并将从动态子结构方法在本模型中的使用、解析算法的构建,瞬态动力学响应的求解与分析,以及实验验证等方面对仿生构件在足地接触瞬间的动力学响应过程进行求解。

1 仿生构件的动态子结构模型

移动机器人仿生构件通常采用铝合金、工程塑料等质量轻、力学性能优异的金属和非金属材料,以达到能源供给、装载运输、仿生性能发挥的等的综合指标。仿生机构的足端在与地面接触时,承受着来自全身的压力,同时需要克服惯性影响以及位置身体重心稳定等多种作用,因此,本文以仿生机构足地接触的动态模型为基础,对足端接触地面瞬间的动力学响应进行研究。机器人足端通常简化为杆构件与地面接触,因此足地接触模型可简化为图1所示的基于动态子结构的碰撞系统。其中固定面代表地面,杆垂直于地面,同时受到关节力F的作用,加速向地面运动,与地面发生碰撞,其中,自由杆长度L,横截面积A,弹性模量E,碰撞前距离地面的高度为H,假设在碰撞过程中不发生塑性形变,杆不发生屈曲,地面为刚性体不发生弹性变形,撞击接触面摩擦系数为零,撞击力垂直于公共面,应力波只沿着杆轴线传播,忽略应力波的几何弥散。

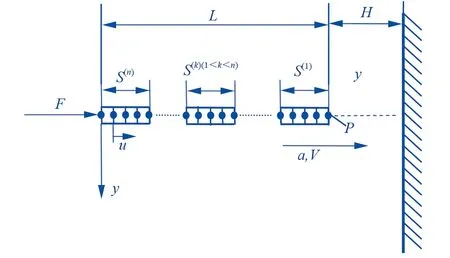
图1 碰撞系统子结构模型

动态子结构方法为简化计算模态阶数而采用的数值求解方法,关于动态子结构方法,如图1所示,将碰撞杆离散为n个长度相同的子结构,每个子结构划分成m个二节点杆单元,节点P为碰撞节点,u为节点的物理位移,子结构S(k)的运动方程为:

(1)

式(1)即为构件运动的振动平衡方程,因为足端触地时间极为短暂所以采用动态平衡方程进行求解,阻尼系数C此处为零,其中,质量矩阵为协调质量矩阵,F为外载荷,R为界面力,物理位移向量u(s)分为两部分:内部节点位移ui(s)和界面节点位移ub(s)。也就是外载荷Fi(s)在界面固定不动时作用在子结构内部所产生的位移,与界面位移ub(s)所产生的静态位移。则物理位移向量u(s)可表示为:

(2)

(3)

式中 :

(4)

在杆垂直碰撞地面时,碰撞的约束条件可以表示为式(5):

Fc(t)≥0Fc(t+△t)<0

(5)

式(5)中:Fc为碰撞接触力,式(5)通过接触力的大小或者正负来判断柔性体与地面之间的接触状态,当接触力Fc大于等于0时,说明地面与柔性体之间保持接触[15]。

2 瞬态响应特性分析

首先选取腿机构常用材料铝合金为主要研究对象,设定计算所用参数如下:铝合金材料弹性模量:E=7×1010Pa,简化后的杆长L=0.16 m,杆的横截面积A=0.000 1 m2,杆碰撞前距接触面H=0.15/0.3 m,屈服强度σ0.2=582 MPa,还有所加载的不同载荷等其他条件将在下面的分析过程中进行说明。

基于两节点干单元,利用动态子结构方法进行分段,每4个节点杆为一个子结构,依据收敛情况进行总结点数目的确定,L杆长暂且分为50个子结构,对每个子结构进行主模态求取,且该动态子结构划分方法已经过证明收敛:

(6)

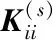
2.1 应力波

在足地接触瞬间应力将沿着杆长以波动形式传播,并将在杆长的另一端进行反射,形成一定的应力波现象,因此本文首先进行瞬态响应的应力波求解。

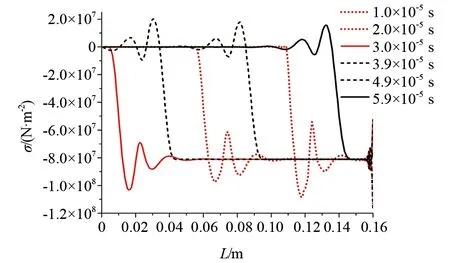
图2 应力波在杆中传播

图2为在0.5 kg载荷作用下,应力波沿杆长传播一个周期,约为6.28×10-5s时,杆中应力的存在情况。前半周期,波沿杆长从接触侧一端向另一自由端移动,且应力波形面的变化较为迅速,将在自由端进行反射。在波形面变化前后,应力波的幅值较为稳定,保持原幅值不变。在接触应力波沿杆长自右向左传播过程的同时,由于加载质量的作用,所产生的载荷应力波同时自左向右,由自由端向接触端传播,传播速度与接触应力波相同,并将在接触端进行反射。相比于接触应力波,载荷应力波的幅值较小,对杆整体的动力响应影响较小,暂且忽略。

图2在不考虑构件与载荷重力条件下进行计算,然而,足地接触过程通常受到重力影响,因此在重力作用下,应力波在杆中的传播情况如图3所示。

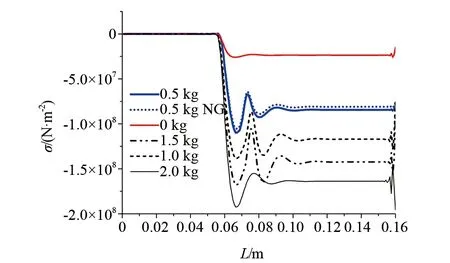
图3 考虑重力条件下应力波在杆中的传播情况

图3所示,为杆中应力波在0.2×10-5s时杆中的应力传播情况,其中上端实线为无外部作用力条件下,杆从0.15 m的高度自由落体,接触应力波在杆中的传播情况;蓝色多点线型为不考虑重力,杆在0.5 kg外载荷作用下杆中的应力波状态,与考虑重力条件下的应力波(蓝色实线型)相比,存在一定的差异,相对较小,这主要是由于两种情况下,杆碰撞的初始速度不同造成的。其余三条曲线分别为考虑重力条件下,杆在不同载荷作用下的应力波传播情况,三条曲线具有相似的传播特性,因碰撞初速度的不同而具有不同的应力幅值。

2.2 速度波

代表铝合金材质的一维杆内,碰撞应力波与加载应力波分别以一定的速度沿杆长方向体向另一端传播,速度波与应力波具有相似的传播形式,如图4所示,碰撞应力波到达加载端之前,速度波向左侧碰撞端传播,铝合金材质杆内各点速度逐渐降低,并将在加载端,速度波将反射以相同幅值由左侧向右侧传播,图4为0.20×10-5s时铝合金材质杆在0.5 kg、1 kg、1.5 kg载荷作用下以及碳纤维杆在1.5 kg载荷作用下,速度波的传播形式,因为作用在碳纤维杆上的载荷较大且碳纤维杆材质较轻(0.028 8 kg),所以具有较大初始速度,且因为碳纤维材质杆的弹性模量较大(230 GPa),所以,速度波在杆长传播的速度较快,在0.20×10-5s时刻,速度波形面经过加载端反射并向接触端传播。

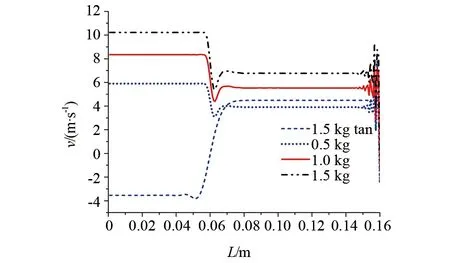
图4 速度波在沿杆长的分布情况

由图4内速度波的波形面可以发现,简化后的一维杆内各点速度在传播过程中逐渐降至最低并开始反向运动。速度波的波形面变化较为迅速,这与图5所示杆内加速度波的变化形式有直接关系。

图5 加速度波沿杆长的分布情况

2.2 加速度波

由图5所示,不同的载荷加载情况下,加速度波在传播过程中始终存在较为明显波动峰值,并且随着时间推移加速波的峰值将逐渐减小,波宽将逐渐增加,如图5所示。在0.2×10-5s时,两中材质杆,以及不同加载条件下,加速度波峰值分别与图3,图4的碰撞应力波与碰撞速度波相对应。

加速度波在传播过程中,波峰附近的质点加速度波动变化较为明显,由波峰迅速降至最低值,并在波峰两侧成对称分布,因此远离波峰的质点加速度波动较小,这也使得速度波及应力波沿杆长呈一定的常数值变化。

2.4 位移波

与速度波、加速度波不同,位移波的变化具有一定的线性,如图6所示,6.28×10-5s的时间内,位移波前端出现了斜率一定的直线段,表明位移波在传播过程中,斜线段部分的位移保持不变,所以,在碰撞接触过程中,铝合金材料杆表现出了较为明显的弹性运动。在应力波反射回碰撞接触端时刻,位移波在杆内开始由正变负,此时,杆内各质量点开始脱离碰撞接触阶段,沿相反方向作腾空弹起运动。

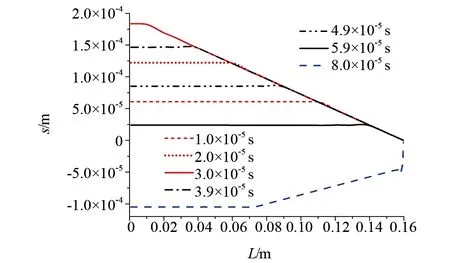
图6 位移波随时间推移沿杆长传播情况

如图6所示8×10-5s时,位移为负值,杆长已经与刚性面脱离接触,完成了第一次弹性碰撞。

3 实验验证

为验证所计算模型的正确性,本次研究利用高速摄像系统对铝合金材质的仿生构件与刚性面碰撞接触进行了实验记录。

本次实验,采用高速摄像的拍摄频率为>2 000 帧/S,镜头采用1∶1比例专用镜头。

图7所示图像由高速摄影仪记录完成,记录时间为5×10-4s,由3×3图列的比较可以发现,在第二行第一幅图时,杆与刚性面接触,在第二行第二幅图时杆与刚性面迅速脱离接触,并已经与刚性面见有了一定的位移,即可以得出碰撞接触时间远小于5×10-4s,如因此,碰撞接触过程在5×10-4s内已经完成,这与图6所示计算结果初步吻合。

图7 铝合金杆的碰撞记录实验

4 结论

本文通过将铝合金杆件进行模型简化,引入动态子结构方法,对仿生构件常用材料的应力波、速度波、加速度波以及位移波沿着杆长的传播特性进行求解,将仿生机构足地接触状况应用于仿生构件与刚性面的接触碰撞的简化模型中,获得了不同条件下,仿生构件内部的瞬态响应特性,并最终采用高速摄像系统对柔性系统的碰撞过程进行了实验记录,结果表明所获得的数值模型及结果对仿生机构性能的研究具有良好的借鉴作用。