接触状态感知下分拣机器人抓取过程多参数挖掘控制技术

张鹏伟, 李学威

(周口职业技术学院 信息工程学院,河南 周口 466000,;E-mail: zhanghu54545@yeah.net)

分拣机器人是由传感器、物镜和电子光学系统组成的机器人,具备多种功能,能够实现对商品的快速分拣。随着快递物流行业的高速发展,大量货物需要分拣,部分大型物流中心选择采用分拣机器人代替人工分拣[1-2]。目前分拣机器人在控制方面技术不够成熟,分拣机器人在分拣大型包裹时力量优于人工,分拣小型包裹时机械臂精准度不足,易存在漏捡或掉落情况。若分拣机器人运送包裹至目标处时,受障碍物影响或其他原因可能导致机器人运行线路失误[3]。因此,如何精确地控制分拣机器人是目前学术界的一个重要课题。

王敏等[4]采用改进的粒子群技术实现了食品分拣机器人的动态目标抓取控制。通过改进传统粒子群,对食品分拣机器人动态目标抓取动作进行控制,虽有效提升分拣机器人的分拣效率,但分拣机器人对小目标食品进行抓取的效果还有上升的空间。董豪等[5]利用深度强化学习方法,实现了机器人的运动控制。采用深度强化学习算法,对机器人运动轨迹进行控制,虽然能够使机器人运动轨迹稳定,但机器人运行效率较低。

针对上述问题,提出了接触状态感知下分拣机器人抓取过程多参数挖掘控制技术。通过力传感器获取接触状态的信息,根据时间序列构造数据集,并对不同的时间序列进行了离散化处理,利用模糊PID控制算法对分拣机器人进行控制,引入模糊隶属度函数及模糊控制关联规则,对关键参数进行挖掘,并将挖掘结果输入到模糊PID控制器中,完成分拣机器人多参数群体挖掘控制。

1 接触状态感知下分拣机器人多参数选取

1.1 接触状态问题分析

在分拣机器人的控制过程中,由于货物存在着复杂的结构形状和位置随机分布等诸多因素,使其难以有效描述控制过程中的接触状态[6]。因此,通过力传感器[7-8]来获得接触状态的信息是实现分拣机器人控制的关键。

在t时刻,分拣机器人机械臂末端的接触状态为:

ζt=[FX,FY,FZ,εX,εY,εZ,X,Y,Z,ωt,ψt,υt]

(1)

式中:FX,FY,FZ分别表示分拣机器人机械臂末端在坐标X,Y,Z中的力;εX,εY,εZ分别表示在坐标X,Y,Z中,通过力传感器获取的分拣机器人机械臂末端操纵力矩,ωt,ψt,υt分别表示t时刻,分拣机器人机械臂末端接触状态的特征属性。

在实际的分拣要求下,将分拣机器人控制与货物之间的接触过程视为一种接触状态,也就是真实的接触状态是一个多变量的时间序列[9]。根据时间序列构造数据集,对不同的时间序列进行了离散化,得到的接触状态Vi表示为:

Vi=[ζ1,ζ2,…,ζn],i=1,2,…,m

(2)

1.2 接触状态感知下分拣机器人多参数获取

在上述接触状态描述下,将PID算法融入模糊控制,利用模糊PID控制算法[10-12]控制分拣机器人,分拣机器人控制总体结构如图1所示。

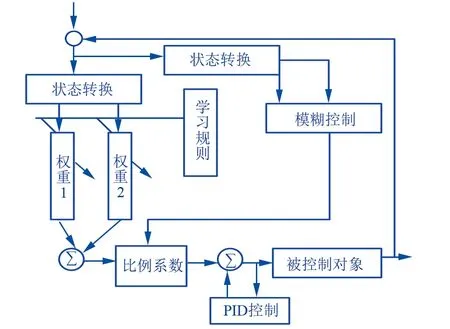
图1 分拣机器人控制总体结构

图1的分拣机器人控制总体结构中包括以下部分:

(1) PID控制利用比例参数、积分参数、微分参数对分拣机器人进行控制。

(2) 模糊控制即对PID控制的输出增益K进行调整,增益K值是分拣机器人控制总体结构稳定的关键。PID算法是利用设定期望值与实际值间的误差值对输出量进行控制,直至实际值与设定期望值贴近为止。在接触状态感知下PID算法控制多参数表达式为:

(3)

公式(3)中:U为通过计算比例参数Kp、积分参数Ki及微分参数Kd获取的被控制量,即分拣机器人控制多参数;E为分拣机器人参数期望值与实际值间的误差值;R为分拣机器人参数设定期望值,并输入R至PID算法;用Y描述控制后分拣机器人参数的实际值;分别用Ti与Td描述积分参数Ki与微分参数Kd的时间常数,转换公式(1)为传递函数表达式:

(4)

公式(4)中:S为收集样本周期。在接触状态感知下PID算法中,调整比例参数Kp、积分参数Ki和微分参数Kd是分拣机器人多参数群体挖掘控制的核心,输出增益K值能够影响分拣机器人控制总体结构的稳定性。

1.3 分拣机器人多参数群体关键参数挖掘控制

1.3.1 PID控制多参数输出增益的模糊自整定

为使分拣机器人控制更加稳定,减少多参数群体设定期望值的盲目性及随机性,随时对输出增益K值进行调整。在接触状态感知下,PID算法控制多参数的基础上,融入模糊控制,利用误差及其变化率调整输出增益K值,达到在接触状态感知下PID算法控制K值的模糊自整定。模糊控制对不易被构建的模型或精准度差的模型进行控制时,控制优势明显。

在Matlab软件上设计Mamdani型模糊控制器[13],将误差及其变化率传送至输入控制器,将融入模糊控制的PID控制K值传送至输出控制器。设定输入和输出的基础论域是[-3,3];模糊论域是{-3,-2,-1,0,1,2,3};模糊语言子集是{负大NB、负中NM、负小NS、零ZO、正小PS、正中PM、正大PB},依据输入与输出的变量,获取对应的隶属度函数。

模糊控制规则通常由专家知识库及实践结合组成,如表1所示。

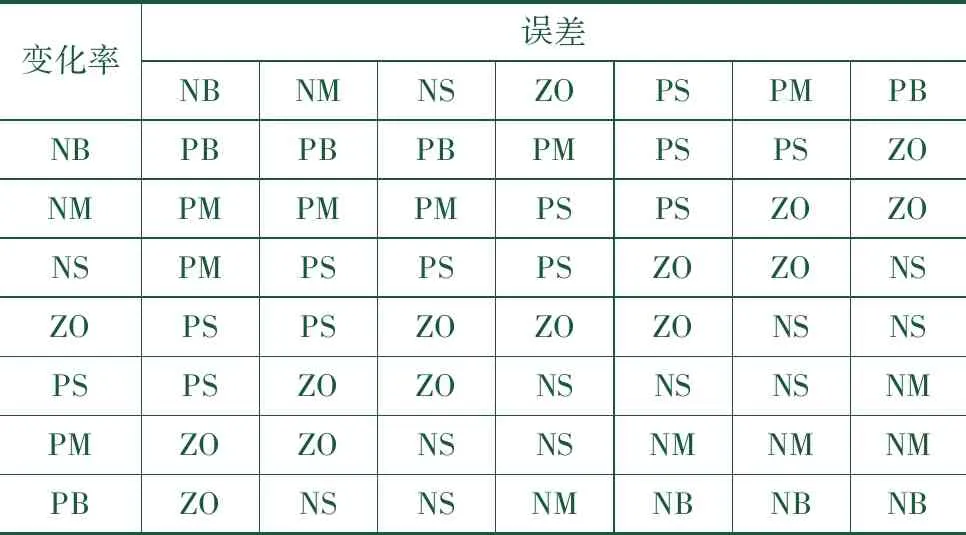
表1 模糊控制规则

通过表1模糊控制规则,获取PID多参数输出增益的模糊自整定标准为:在分拣机器人控制过程中,若误差值高,则通过增加K值提升分拣机器人控制速度与控制时间;若误差值低,则通过减少K值,调整误差,使分拣机器人状态稳定。

1.3.2 模糊C均值聚类的多参数群体挖掘控制

将模糊隶属度函数及模糊控制关联规则引入至聚类分析内,即模糊C均值聚类算法[14-16]。设置模糊隶属度函数矩阵为A,其中行与列分别用m与n描述。任意参数i属于某一簇j的长度用Aij(Aij∈[0,1],i=1,2,…,m;j=1,2,…,n)值描述,此过程为模糊划分,模糊隶属度函数矩阵A所需要符合条件的表达式为:

(5)

设置X=(x1,x2,…,xm)为待聚类数据集,xi为待聚类数据对象,模糊划分数据集为n类。将欧式距离作为聚类效果衡量标准,获取目标函数为:

(6)

公式(6)中,z为模糊加权指数,vj为j次模糊划分获取的聚类中心。

依据拉格朗日乘数法及公式(3)求导,获取表达式为:

(7)

结合并扩展模糊C均值聚类的模糊关联规则,实现分拣机器人多参数群体挖掘控制步骤为:

(1) 依据模糊C均值聚类,挖掘模糊PID控制多参数群体中的模糊关联规则,输入分拣机器人多参数群体等待挖掘,获取符合约束条件的支持度与信任度最小值,关联规则参考A&B⟹C,其中A、B、C代表分类属性。

(2) 通过专家知识库及实践,结合建立相关多参数群体,将其与分拣机器人相关的A、B、C模糊数据,与具备的全部可能组合代入关联规则A&B⟹C,模糊查询并挖掘其模糊关联规则。

(3) 输出分拣机器人多参数群体挖掘结果至分拣机器人控制的模糊PID控制器中,由此实现分拣机器人多参数群体挖掘控制。

2 实验分析

2.1 实验环境与多参数选取

为验证接触状态感知下分拣机器人多参数群体挖掘控制方法的有效性,将所提方法应用于某物流中心,抽取该物流中心编号1至编号10分拣机器人进行分拣控制实验。为避免随机性对控制结果的影响,在所提方法控制下通过10个分拣机器人完成该物流中心部分货物分拣。10个机器人均为协作机器人,驱动方式为双轮差速,最大载重量为30 kg,机器人关节数量为6个,关节长度为0.5 m,机械臂质量为1.5 kg。对该环境仿真:

① 下载并安装MATLAB里的 Robotic机器人工具箱。

② 编写机器人位姿运动学方程,即给定关节变量,求解机器人末端相对于基坐标的齐次变换矩阵。并在此基础上,用工具箱里的命令fkine验证程序的正确性。

③ 编写机器人速度运动学中求解雅克比矩阵的程序,并在此基础上,用工具箱里的命令jacob0验证程序的正确性。

④ 使用机器人工具箱建立机器人连杆模型,并在此基础上,绘制机器人工作空间,分拣机器人仿真图如图2所示。

图2 分拣机器人仿真图

为验证所提方法采用模糊C均值聚类算法实现多参数群体挖掘控制有效性,统计不同模糊加权指数时,采用所提方法进行多参数群体挖掘的调整兰德系数,调整兰德系数通过优化兰德系数,可有效解除兰德系数在评估时受随机标签的限制。结合模糊C均值聚类算法与实际标签,设置X={X1,X2,…,Xi}为通过聚类获取的簇集;Y={Y1,Y2,…,Yj}为依据实际标签更新后的聚类结果集,则调整兰德系数表达式为:

(8)

公式(8)中,nij为Xi和Yj交集处的样本个数,即nij=|Xi∩Yj|,ai为Xi的样本个数,bj为Yj的样本个数。ARI的阈值是[-1,1],且ARI值越高,聚类效果就越好,多参数环境及调整兰德系数如图3、图4所示。

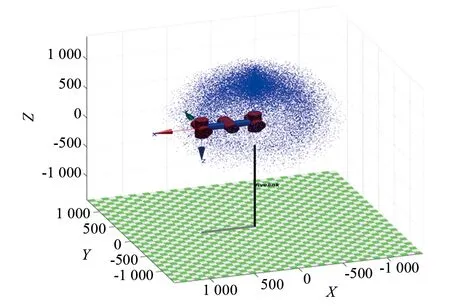
图3 多参数机器人控制环境仿真图

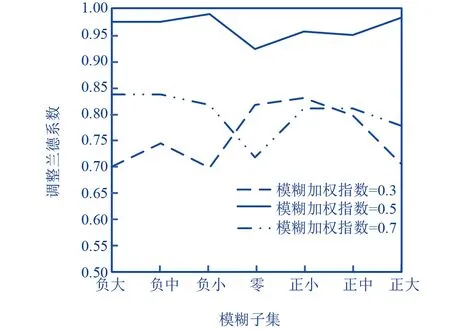
图4 多参数群体挖掘的调整兰德系数

通过图4实验结果可以看出,当模糊加权指数为0.5时,所提方法调整兰德系数均高于0.9;当模糊加权指数为0.3以及0.7时,所提方法调整兰德系数处于0.7-0.85之间。由此可知,所提方法采用模糊C均值聚类算法实现多参数群体挖掘控制时,模糊加权指数为0.5,具有最优的挖掘性能,为分拣机器人的精准控制提供基础。

2.2 实验结果统计与分析

采用所提方法控制10个分拣机器人完成897个物流包裹的分拣,在物流中心的货物分拣状况如图5所示。

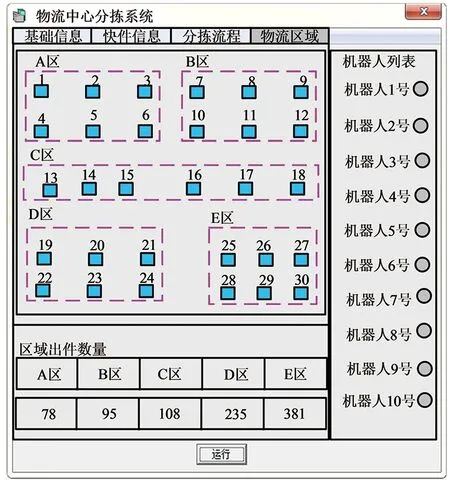
图5 分拣机器人分拣界面图

通过图5实验结果可以看出,采用所提方法对分拣机器人进行控制,分拣机器人可以依据设定的分拣目标,自动分拣目标包裹。物流中心的10个分拣机器人在五个区域内分拣包裹总数量为897个,与设定的包裹分拣数量相同。由此可知,所提方法未出现误分拣情况,各区域出件数量精准,表明所提方法的分拣机器人控制效果良好。

2.2.1 移动距离

为进一步验证采用所提方法控制分拣机器人移动状态下的控制性能,统计分拣机器人跨区域分拣时的目标距离与机器人实际移动距离,实验结果如图6所示。

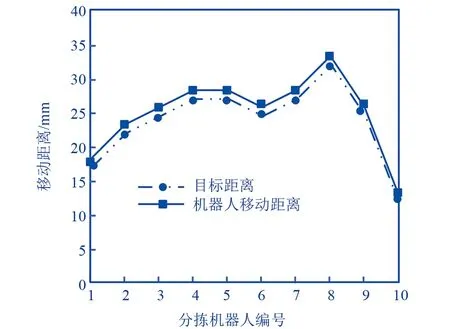
图6 分拣机器人移动距离对比

通过图6实验结果可以看出,采用所提方法控制分拣机器人的实际移动距离与目标距离的吻合度较高,验证所提方法可以有效控制分拣机器人,令分拣机器人移动至目标位置。由此可知,所提方法具有较高的分拣机器人控制精度,保证分拣机器人在远距离包裹分拣中良好运行。

2.2.2 运动轨迹控制

在此基础上,验证所提方法对分拣机器人机械臂控制情况,实验在物流中心分拣过程中,记录分拣机器人机械臂的期望与实际运动轨迹,实验结果如图7所示。

根据图7实验结果可以看出,采用所提方法控制分拣机器人机械臂,可以依据期望运动轨迹控制分拣机器人机械臂。分拣机器人在分拣包裹时,机械臂输出的运动轨迹与期望运动轨迹相差较小,验证所提方法具有良好的分拣机器人控制性能。

2.2.3 避障误差

为验证采用所提方法控制分拣机器人的准确性,实验在物流中心五个区域内设置不同类型障碍物,观察分拣机器人在运行过程中,对障碍物的避障误差,实验结果如图8所示。

图8 分拣机器人避障误差

通过图8实验结果可以看出,采用所提方法控制分拣机器人,其在X轴、Y轴、Z轴坐标位置的避障误差均低于1 mm,由此验证了所提方法具有较高的分拣机器人控制精度,应用于物流中心的包裹分拣时,具有良好的避障应用性能。

2.2.4 分拣动作控制

进一步验证采用所提方法控制分拣机器人在分拣小件包裹时的有效性,实验对物流中心的10台分拣机器人进行不同次数的分拣测试,分别测试分拣机器人在分拣小件包裹时,抓取、抬起与松开三种动作的实际控制结果,统计结果如表2所示。

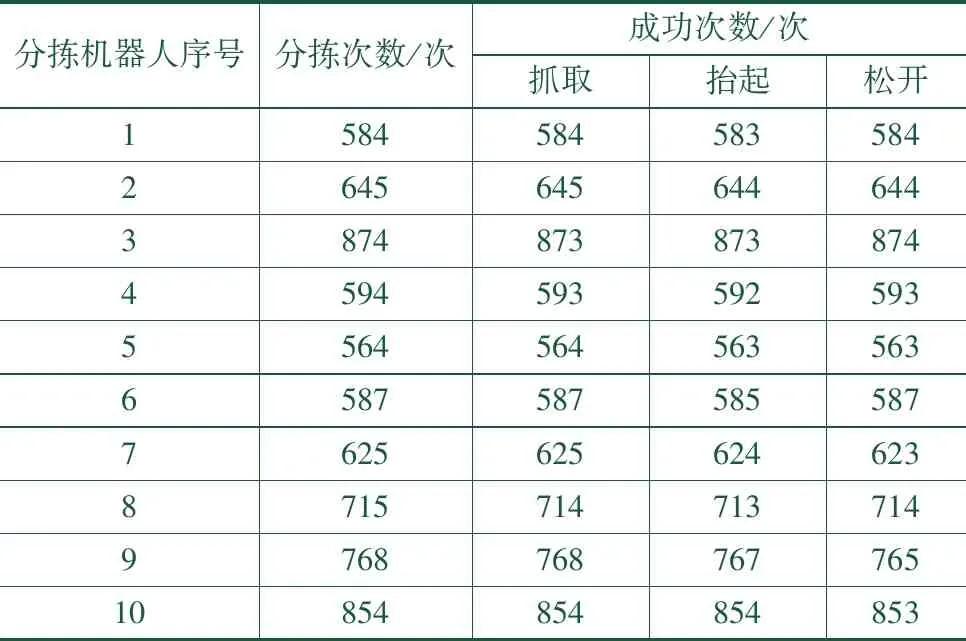
表2 分拣机器人分拣动作控制结果

通过表2实验结果可以看出,采用所提方法控制分拣机器人,仅存在少量的动作失败情况,能够良好地完成分拣包裹所需的抓取、抬起与松开动作,分拣失败次数均低于0.5%。再次验证了所提方法控制分拣机器人动作有效性。

2.2.5 抓取速率

统计采用所提方法控制分拣机器人在不同传送带速度时的抓取速率,统计结果如图9所示。

图9 分拣机器人抓取速率

观察图9实验结果可以看出,分拣机器人的抓取速率随传送带速度升高而提升,采用所提方法对分拣机器人进行控制,在不同传送带速度时的抓取速率均高于1.5个/s,表明通过所提方法控制分拣机器人的抓取速率较高,为提升物流中心的分拣效率提供良好的基础。

3 结论

为有效控制分拣机器人,提升分拣机器人分拣效率及稳定性,提出了接触状态感知下分拣机器人多参数群体挖掘控制方法。根据分拣机器人机械臂末端的接触状态,获取接触状态感知下分拣机器人多参数。通过模糊控制方法对PID控制多参数的输出增益实施模糊自整定,并选取模糊C均值聚类方法,挖掘模糊PID控制多参数群体中的模糊关联规则,实现分拣机器人多参数群体挖掘控制。通过实验验证,所提方法能够控制分拣机器人抓取、抬起,松开等动作,且分拣机器人抓取速率高,精准程度良好。