沙漠砂蒸压加气混凝土砌块砌体恢复力模型的研究
2023-11-01王玉山牛爱宏
肖 迪,陈 康,王玉山,2,赵 易,牛爱宏,王 迪
(1. 石河子大学 水利建筑工程学院,新疆 石河子 832000; 2. 新疆兵团 高烈度寒区建筑抗震节能技术工程实验室,新疆 石河子 832000)
0 引言
在国家提倡“节能减排”的背景下,建筑业被定为“节能减排“的重点,这一政策的提出为新型建筑材料的开发和应用带来了前所未有的机遇。在新型建筑材料中,蒸压加气混凝土砌块属于重要的墙体材料之一。但目前对蒸压加气混凝土砌块的研究多集中于粉煤灰和矿渣砂加气混凝土砌块,而对沙漠砂蒸压加气混凝土砌块的研究较少。课题组针对这一问题,同时考虑到新疆沙漠砂资源丰富的情况下,将沙漠砂替代河沙成功地研发了一种新型建筑材料——沙漠砂蒸压加气混凝土砌块[1],遵循了“因地制宜、就地取材”的原则。该种建筑材料与普通的加气混凝土在组成成分及特点上虽有很多相似之处,但是沙漠砂颗粒极细,风化表面光滑且活性较差,要将沙漠砂蒸压加气混凝土砌块应用于实际工程中,仍需更深入地研究。恢复力模型是通过适当地抽象和简化从大量试验中获得的恢复力与变形之间的关系曲线而得出实用数学模型,也是进行结构地震分析的理论基础[2-3]。
在结构弹塑性动力分析过程中,选取恰当的构件和结构恢复力模型是结构分析与计算的基础。寇佳亮等[4]对6个HDC加固震损古旧砌体试件进行低周往复荷载试验,提出了适合HDC加固震损古旧砌体结构的恢复力模型;周铁钢等[5]对新型机制生土砖砌体墙进行拟静力试验,并建立了四折线骨架曲线模型,无量纲化试验数据与模型吻合良好;LAN等[6]对9个联锁式压缩土砌块复合墙体进行低周往复试验,得到了适合该墙体的三线性恢复力模型;XUE[7]等通过对6片钢筋再生混凝土框架填充再生混凝土砌块在低周往复荷载试验的基础上,对试验数据进行拟合分析,得到适用于该墙体的四折线恢复力模型;倪博文等[8]对6个不同洞口位置节能砌块隐形密框复合墙体进行低周反复荷载试验,建立了节能砌块隐形密框复合墙体的四折线恢复力模型;王义俊等[9]通过对6片内置暗支撑剪力墙在低周往复荷载作用下的试验数据进行拟合分析,得出的恢复力模型拟合效果良好。
综上所述,现有针对沙漠砂蒸压加气混凝土砌块墙体恢复力模型研究尚少。因此课题组对已有的采用不同工况砌筑的沙漠砂蒸压加气混凝土砌块墙体低周往复荷载试验数据参考文献[10-11],研究此类墙体的恢复力模型,为此类墙体在地震作用下的非线性动力响应提供参考。
1 沙漠砂蒸压加气混凝土砌体拟静力试验
为了研究不同工况对沙漠砂蒸压加气混凝土砌块性能产生的影响,并得出不同构造方式的恢复力模型。本文选取了10片不同工况的沙漠砂蒸压加气混凝土砌块砌筑墙体,其参数见表1,墙体的高宽比为0.69和0.73相差较小且设计不同的构造方式。通过观察试验破坏形态(见图1),可以看出墙体产生的破坏裂缝,属于剪切型破坏模式。由此可知:墙体的高宽比、墙体的不同设计类型以及竖向压应力都会对墙体的破坏模式产生影响。表1中墙体所使用的砌块均为本课题组研发的B06沙漠砂蒸压加气混凝土砌块,砌块宽度分别是200 mm和250 mm;砂浆强度均采用M7.5;竖向压应力从0.1~0.5 MPa,数据选取较为接近,可为沙漠砂蒸压加气混凝土砌块墙体的恢复力模型研究提供参考依据。

图1 墙体破坏形态Fig. 1 Wall damage pattern

表1 墙体试件参数Table 1 Parameters of wall specimens
2 加载制度
文献[10]水平加载方案为:采用位移加载,刚开始加载时步长控制为0.1 mm,持续8级,加载到0.8 mm,步长控制为0.3 mm,持续34级,加载到11.0 mm,以0.6 mm为步长,持续31级,加载到29.6 mm,每一级重复2次,共计146次循环,并且当荷载下降到极限荷载的85%以下时,试验结束。
文献[11]水平方向同样采用位移加载,以开裂位移Δ为主,再以2Δ、3Δ和4Δ位移进行控制,直到荷载下降到85%为止。其次当在墙体位移达到6 mm之前,加载速率以0.02 Hz加载,当墙体在6 mm以后,加载速率以0.48 mm/s进行加载且每一级循环3次。
3 恢复力模型的建立
滞回规则与骨架曲线模型共同构成恢复力模型,其中:骨架曲线模型能够反映结构或构件的开裂、屈服、峰值及破坏等特征点,并指定结构所有状态点的范围;滞回规则能够直观地了解到结构的刚度退化、耗能性能及滑移等特征[12]。为达到上述要求,需采用准确的计算方法描述恢复力模型。目前,试验拟合法和理论计算法是确定恢复力模型主要的两种方法。试验拟合方法基于水平低周循环反复荷载试验数据和适当的数学模型,定量确定骨架曲线与标准滞回线,最后建立恢复力模型;理论计算法是对已有的恢复力模型加以计算与演化,得到所需的恢复力模型,此方法可以不断地改进现有的恢复力模型。为了更好展现结构在地震作用下滞回规则和骨架曲线,本文先提出理论公式,再根据试验数据确定系数,最后建立该结构的恢复力模型[13]。
3.1 骨架曲线的确定
将试验墙体的滞回曲线同向各次加载级别的峰值点连成的曲线称为骨架曲线[14]。其可以反映出结构或构件在受力与变形作用下的强度、刚度、耗能及延性等众多力学特性。通常为了方便处理,一般选取试验墙体相应的特征点将骨架曲线绘制为折线式。通过骨架曲线可以全面地了解试验墙体在低周反复荷载下的荷载-位移关系。而无量纲归一化骨架曲线是由试件开裂荷载与位移、峰值荷载与位移及破坏荷载与位移三个特征点建立的曲线图,可以直接反映试件由开裂到失效的变形性能差异。
因试验设备、材料的不对称特性以及刚度退化等方面的影响,骨架曲线在正反加载方向常常不一致,通常将骨架曲线进行归一化与平均化。平均化是在同一象限中绘制出正反加载方向的骨架曲线,在同一位移处将两条骨架曲线的荷载平均,大多数试验数据采用此方法;归一化是对骨架曲线进行无量纲化,可消除不同墙体试件之间由于砌块及砂浆强度不同而导致的骨架曲线差异。
以文献[11]为例,如图2骨架曲线所示,可知沙漠砂蒸压加气混凝土砌块砌筑墙体的骨架曲线在达到开裂点后出现明显的上升段,上升至峰值点后出现明显的下降段,因此可采用三折线模型来模拟[15]。取墙体开裂、峰值和破坏三点(开裂点即通过肉眼观察到初始裂缝的荷载级,峰值点为骨架曲线的最高点,破坏点以峰值荷载的85%确定作为破坏状态)对应的荷载和水平位移作为特征点,并对特征点进行无量纲归一化,即三个特征点的水平荷载与位移分别除以峰值荷载Pu与峰值位移Δu。以P/Pu为纵坐标,以Δ/Δu为横坐标,建立无量纲三折线归一化骨架模型,各工况下的归一化骨架曲线如图3所示。
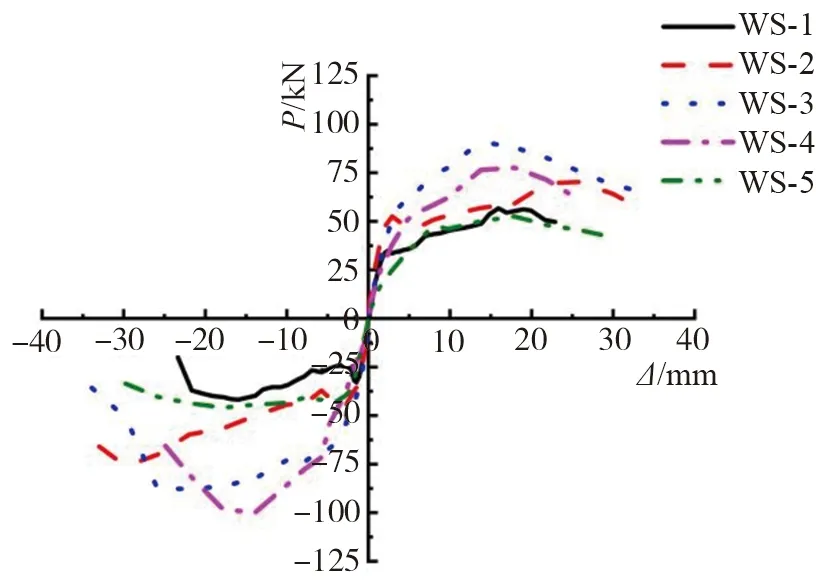
图2 文献[11]荷载-位移骨架曲线Fig. 2 Load-displacement skeleton curve in literature [11]

图3 归一化骨架曲线Fig. 3 Normalized skeleton curve
3.2 弹性阶段刚度K0
由图3可知:归一化的骨架曲线分成了三段,分别是:弹性段(OA段)、弹塑性段(AB段)及下降段(BC段)。根据相应文献数据及试验现象,现浇式构造柱约束墙体与装配式构造柱约束墙体的初始刚度K0均高于无约束砌块墙体初始刚度K0,可知在小震的情况下装配式构造柱约束的墙体变形不明显,抗震性能优于无约束砌块墙体。而现浇式构造柱约束的墙体初始刚度K0小于装配式构造柱约束墙体初始刚度K0,表明装配式构造柱对于墙体弹性阶段初始刚度的提升优于现浇式构造柱。无约束砌块墙体、现浇式构造柱约束的墙体和装配式构造柱约束墙体初始刚度K0分别为2.360、2.960和4.158。
3.3 弹塑性阶段刚度K1
从图3归一化骨架曲线可以看出:无约束砌块墙体、现浇式构造柱约束的墙体和装配式构造柱约束墙体的弹塑性阶段限度都比较平缓。但从表2中可以看出:无约束砌块墙体与装配式构造柱约束墙体在弹塑性阶段的刚度K1比较接近0.516和0.490。而现浇式构造柱约束墙体在弹塑性阶段的刚度K1均高于前两种工况的K1,与3.2节不同,现浇式构造柱对K1值的提高较为明显,表明此阶段现浇式构造柱已逐渐发挥作用,对墙体的刚度产生影响,其刚度为0.647。

表2 归一化骨架曲线参数Table 2 Normalized skeleton curve parameters
3.4 下降阶段刚度K2
由图3和表2可知:装配式构造柱与现浇式构造柱墙体的K2值比较接近,表明现浇式构造柱在延缓试件下降段刚度退化率的作用与装配式构造柱相当。另外,各工况归一化骨架曲线与数据的对比显示:带构造柱墙体的下降段较为平缓,而无构造柱约束的墙体下降段刚度退化速率较快,一是因为构造柱在砌体结构部分彻底丧失承载力后形成“弱框架”结构体系对墙体的脆性破坏起限制作用;二是由于构造柱与砌体主体结构起到协同作用。
3.5 各阶段刚度方程
墙体开裂前基本处于弹性阶段,将原点与开裂点连线所得的斜率定义为此阶段的刚度K0。墙体开裂后刚度显著降低,随着位移的增加,水平荷载继续提高,当构件进入弹塑性阶段后,将开裂点与峰值点之间连线所得的斜率定义为这一阶段的刚度K1。墙体在达到峰值荷载后,位移增大的同时水平力逐渐下降,负刚度出现,把峰值点和破坏点(取峰值荷载的85%对应的点)之间连线所得的斜率定义为墙体下降段的刚度K2。根据以上描述,即可得到三折线骨架曲线模型计算式如下:
OA弹性段:
P/Pu=K0Δ/Δu
(1)
AB弹塑性段:
P/Pu=K1Δ/Δu-K1+1
(2)
BC下降段:
P/Pu=K2Δ/Δu-K2+1
(3)
由表2所示刚度数值并根据以上计算式建立如下所示的不同工况下墙体的刚度方程:
①无约束砌块墙体,K0=2.360,K1=0.516,K2=-1.332
OA段:
P/Pu=2.360Δ/Δu
(4)
AB段:
P/Pu=0.484+0.516Δ/Δu
(5)
BC段:
P/Pu=2.332-1.332Δ/Δu
(6)
②现浇式构造柱约束墙体,K0=2.960,K1=0.647,K2=-0.591
OA段:
P/Pu=2.960Δ/Δu
(7)
AB段:
P/Pu=0.353+0.647Δ/Δu
(8)
BC段:
P/Pu=1.591-0.591Δ/Δu
(9)
③装配式构造柱约束墙体,K0=4.158,K1=0.490,K2=-0.474
OA段:
P/Pu=4.158Δ/Δu
(10)
AB段:
P/Pu=0.510+0.490Δ/Δu
(11)
BC段:
P/Pu=1.474-0.474Δ/Δu
(12)
3.6 刚度退化回归曲线
利用试验所得的滞回曲线能够计算出试件处于不同位移时的刚度,刚度计算相关公式采用《建筑抗震试验方法规程》规定的割线刚度表示,对试验墙体计算出的刚度回归分析,以获得刚度衰减方程[16],如图4所示为试验散点图与拟合的曲线图,由图可见:拟合曲线均满足于指数衰减方程曲线。各工况对应的方程如下:
①无约束砌块墙体刚度衰减方程
K=e(-0.09Δ+3.17)
(13)
②现浇构造柱约束墙体刚度衰减方程
K=e(-0.04Δ+3.58)
(14)
③装配式构造柱约束墙体刚度衰减方程
K=e(-0.07Δ+3.53)
(15)
通过图4刚度衰减曲线,可以分析得到:
1)通过图4(b)和图4(c)可以得出:尽管构造柱的形式不同,但是刚度退化呈现的规律基本相同。在试验墙体开裂前且位移较小时,退化刚度比较缓慢,基本上保持平稳,随后刚度持续退化。在墙体处于开裂后状态时,试验墙体刚度退化速率加快,随着墙体主裂缝的出现,刚度退化逐渐减缓,表明墙体刚度与内部开裂程度相关。
2)通过图4(a)、图4(b)和图4(c)可以得出:无论是无约束砌块墙体还是带构造柱的墙体,墙体所承受的竖向压应力的增加都能够延缓刚度退化的速率。通过分析可知:竖向压应力的增加使得砌块间的摩檫力增加,从而约束了墙体裂缝的开展。并且设有构造柱墙体在前期的刚度退化速率比无约束砌块墙体更快,在后期渐渐趋于稳定,而无约束砌块墙体在后期将持续退化。
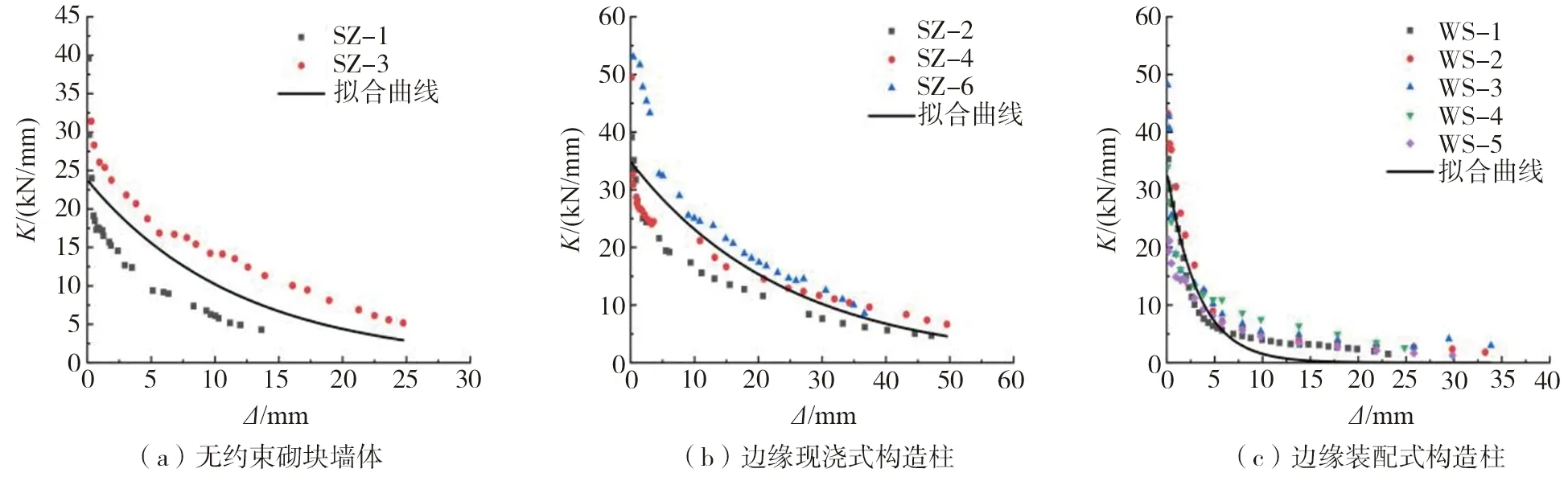
图4 刚度衰减曲线 Fig. 4 Stiffness decay curve
4 滞回规则的确定
以文献[10]中无约束砌块墙体SZ-3试验为例(其他工况的试验与此相似),从试验中所得滞回曲线可以看出如图5所示,滞回曲线出现捏缩现象,开裂前刚度基本保持不变,开裂后刚度退化较大,过峰值点后强度降低,卸载刚度衰减较快。开裂前,墙体的滞回曲线基本呈线性变化,刚度退化较小,可用原点与开裂点之间的连线表示。

图5 SZ-3墙体滞回曲线(数据来自文献[7]试验) 图6 SZ-3开裂后单圈滞回曲线 Fig. 5 SZ-3 wall hysteresis curve (data from literature [7] tests) Fig. 6 SZ-3 single-turn hysteresis curve after cracking
开裂后则与此不同,图6为墙体开裂后单圈滞回曲线,可以看出:加载刚度基本保持相同,可用最大荷载点B(或A)与零荷载点E(或F)之间连线的斜率表示,而卸载刚度退化较快。基于试验得到的不同工况墙体的无量纲化骨架曲线模型,考虑卸载刚度衰减、强度退化及包辛格效应等因素的影响,最终建立无约束砌块墙体(a)、边缘现浇式构造柱墙体(b)与边缘装配式构造柱墙体(c)的滞回规则,其滞回规则如图7所示,以无约束砌块墙体滞回规则为例,对其滞回规则进行如下描述:
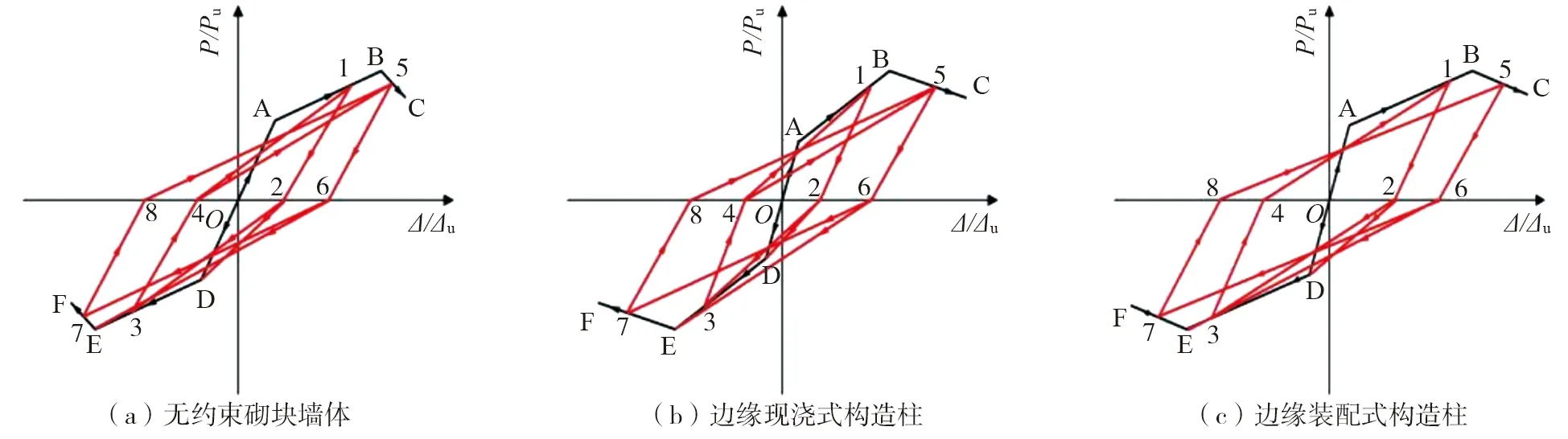
图7 墙体滞回规则Fig. 7 Wall hysteresis rule
1)在加载初期,试件处于弹性状态时,此时可以判定加载刚度不会发生改变,且卸载后无残余变形,正、负向加载和卸载分别沿直线OA与OD段进行,加载和卸载刚度同试件初始加载刚度保持一致。
2)当试件加载达到开裂荷载,但未达到峰值荷载时,正载荷路径沿O-A进行,负载荷路径沿O-D进行;在卸载阶段,由于试件刚度退化,在点1卸载后,正卸载路线沿路径的1-2段进行;当负荷载从点2开始时,若试件负向未达到开裂状态,则加载路径指向屈服点D,那么2-D段为负向加载路径;若试件的负向已经处于开裂状态,则加载路线的终点为位移点3,此时,负向加载路径沿2-3段进行。在反向O-D段卸载时,卸载路径由点3指向点4,负向卸载路线则为3-4段。继续正向加载时,若所加荷载的强度小于试件的峰值荷载,则加载路线为4-1段,若大于,则4-5为加载路径。
3)当达到峰值荷载时,沿着正向加载路径B-C段进行加载,负向加载路径沿着E-F段进行,在点5位置进行卸载,卸载路线为5-6段。然后负向加载,如果负向加载未达到负向峰值荷载,则加载路径指向峰值点E,并按照6-E-F段进行;若负向加载已达至峰值荷载,则加载路径的终点为上一级加载时的最大位移点7,按照6-7-F段进行。若发生负向E-F段卸载同时正向加载时,则沿着7-8-5-C段继续进行。
5 滞回曲线与试验结果对比
以试件SZ-3、WS-2与WS-5为例,根据上述建议的滞回规则,骨架曲线及刚度退化曲线,计算出三个试件的滞回曲线,并对试验值与计算值进行对比如图8所示。由图可知:本文得到的恢复力模型的计算结果与试验得到的滞回曲线大致相同。在每个位移循环下,每个试件的承载力和刚度基本一致;当加载达到峰值荷载后,曲线存在较小的误差,这或许是由于归一化的骨架曲线在下降段存在一定的误差。总体来说,计算值与试验结果吻合良好,验证了该恢复力模型的有效性,为后续针对不同工况下沙漠砂蒸压加气混凝土砌体在地震作用下的弹塑性变形分析奠定了理论基础。
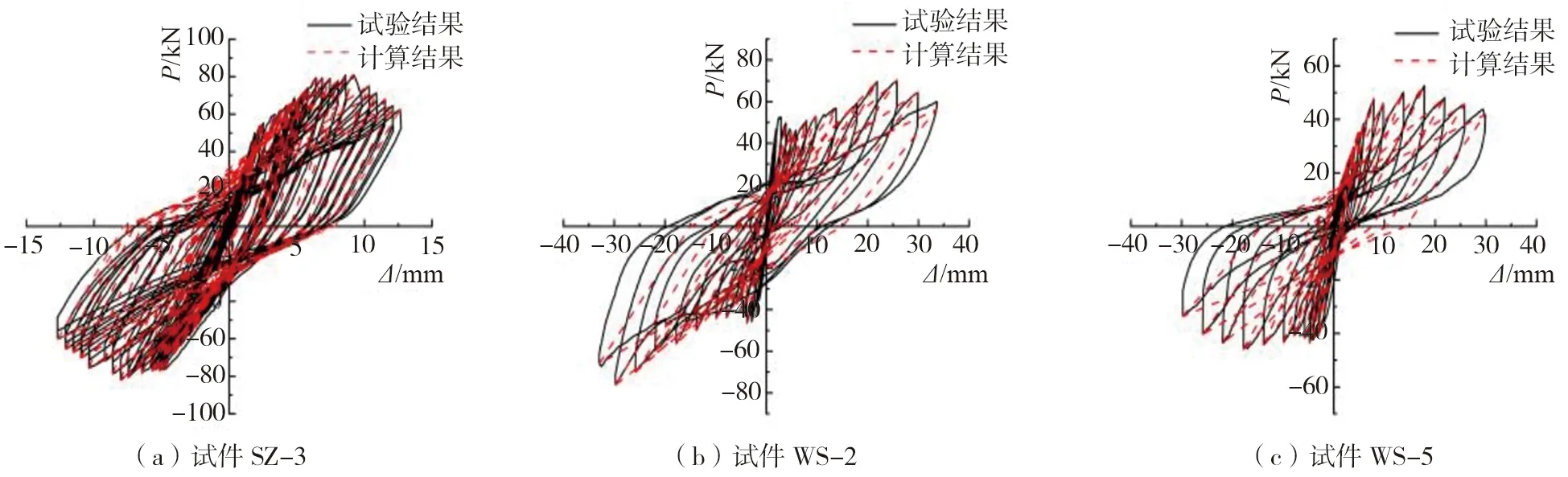
图8 墙体滞回曲线模拟 Fig. 8 Simulation of wall hysteresis curve
6 结论
本文以不同工况下的沙漠砂蒸压加气混凝土砌块墙体为研究对象,基于10片沙漠砂蒸压加气混凝土砌块墙体的拟静力试验,研究了其在水平低周往复荷载作用下的恢复力特性,建立了沙漠砂蒸压加气混凝土砌块无约束墙体、现浇式构造柱约束墙体和装配式构造柱约束墙体的恢复力模型,结论如下:
1)在低周往复荷载作用下,对不同工况的试验墙体采用三折线建立其恢复力模型,通过无量纲归一化骨架曲线,确定了不同工况下砌块墙体各阶段的刚度方程。
2)基于试验得到的不同工况墙体的无量纲化骨架曲线模型,并考虑了卸载刚度衰减、强度退化以及包辛格效应等[17]因素的影响,确定三折线滞回规则。
3)通过恢复力模型的计算结果与试验数据的对比,滞回曲线吻合较好,可为后续沙漠砂蒸压加气混凝土砌块砌体地震弹塑性分析提供技术支撑。
