含软弱夹层场地中地下结构抗震分析的反应位移法误差分析

2023-11-01许紫刚李淳宇庄海洋徐长节

世界地震工程 2023年4期

许紫刚,李淳宇,庄海洋,张季,徐长节

(华东交通大学轨道交通基础设施性能监测与保障国家重点实验室,江西南昌 330013)

0 引言

城市地铁工程作为现代城市交通系统的骨干,对提升城市公共交通运行效率、缓解交通拥堵、优化城市空间结构布局和改善城市环境起到了至关重要的作用。地铁地下结构被土体包裹,过去很长一段时间里地下结构被认为具有较好的抗震性能,因此未对地下结构的防震减灾等问题给予足够的重视。然而,震害资料表明:在地震作用下,地铁车站和隧道结构同样会出现不同程度的破坏[1-2]。从1995年日本阪神地震造成大开地铁车站完全塌毁以后,地下结构抗震研究在理论分析、模型试验和数值模拟等方面都取得了明显的研究进展[3-5]。

岩土介质是影响地下结构稳定性的重要因素之一。软弱土层通常孔隙率高和含水量大,表现出抗剪强度低等特点。地震作用下,软弱土层较其他土层会出现较大的变形,而岩土介质的大变形则会引起地下结构的地震损伤甚至破坏。薄景山等[6]利用一维等效线性化波动方法分析研究了软弱土层埋深和厚度等对场地地表加速度峰值的影响,为软弱夹层场地中结构的抗震设计提供了参考;黄润秋等[7]针对软弱夹层对地震波强度的影响进行了研究,发现了软弱夹层对地震波的放大作用主要与地震波波速有关等规律;陈国兴等[8]研究了软弱土层埋深和厚度对深厚软弱场地中的地表加速度峰值和加速度放大系数的影响;庄海洋等[9-11]在改变软土层厚度和埋深的前提下,对地铁车站地震反应进行数值模拟,得到了软土层性质变化与结构内力、位移之间的关系;李伟华等[12]通过数值计算发现软弱夹层对地铁车站结构地震动响应具有非常不利的放大作用,且当软夹层位于地铁车站中部时,放大作用最不利;杨陶[13]通过结构几何缩尺比为1:30的振动台试验和数值模拟等手段分析了软弱夹层对地下结构抗震分析的影响,结果表明当软弱土夹层位于结构底部时软弱夹层起到的减震效果最为明显;冯帆[14]、窦远明等[15]和吴晔等[16]通过数值分析发现:当软弱夹层位于地下结构中部并且具有一定厚度时,地下结构的地震反应较常规均匀场地条件中的反应强烈,在实际工程设计中应对软弱夹层的存在予以足够的重视。

在地铁地下结构抗震设计方面,早期主要有借鉴地面建筑结构抗震设计的地震系数法和考虑自由场变形为主要荷载的自由场变形法、柔度系数法[17]。为进一步考虑岩土介质与地下结构之间的相互作用,反应位移法和反应加速度法分别通过引入地基弹簧和建立土-地下结构整体分析模型来提高计算精度。目前,反应位移法和反应加速度法已纳入《城市轨道交通结构抗震设计规范》(GB 50909—2014)[18]和《地下结构抗震设计标准》(GB/T 51336—2018)[19]。

反应位移法因其简单高效及易理解的优点,获得了广大设计工作者的认可,并在地下结构抗震设计中具有广泛的应用。反应位移法作为简化抗震分析方法,采用均一性质的地基弹簧作为土体变形力的施加载体,在均质场地中具有较好的计算精度[20]。但含软弱夹层场地中仍采用均质弹簧是否能准确显示出软弱夹层作用效果,结构计算精度有无变化尚需要进一步研究。该研究通过建立不同软弱性质的含软弱夹层场地的计算工况,以整体动力时程分析方法计算结果为基准,对比反应位移法在含软弱夹层场地中的计算精度,从而判定反应位移法在含软弱夹层场地中的适用性。

1 分析方法简介

1.1 反应位移法

《城市轨道交通结构抗震设计规范》(GB 50909—2014)[18]建议的反应位移法计算模型如图1所示,通过在地下结构周边引入法向和切向的弹簧考虑场地土层与地下结构之间的相互作用,在此基础上考虑三部分地震荷载,包括土层相对位移、结构周围土层剪力和结构惯性力。

图1 反应位移法计算模型Fig. 1 Calculation model of response displacement method

通常,地下结构周围的地基弹簧刚度系数可采用经验公式或静力有限元方法进行确定。土层位移可通过以下两种方式施加在结构上:其一是将土层相对位移直接作用在弹簧远离结构的端部;其二是将土层相对位移通过弹簧刚度系数转换为等效荷载后施加在结构上,换算公式如下:

p(z)=k[u(z)-u(zB)]

(1)

式中:p(z)为直接施加在结构上的等效荷载,k为地基弹簧刚度,u(z)为深度z处自由土层地震反应位移,u(zB)为结构底部zB处的自由土层地震反应位移。以上两种方式对反应位移法的计算效果是一致的。此外,土层剪力和惯性力则直接施加在结构上。需要说明的是:土层相对位移、土层剪力及结构惯性力均可通过一维场地地震反应分析获得。

1.2 动力时程分析方法

为评价反应位移法在软弱夹层场地中地下结构抗震分析的计算误差,该研究同时采用动力时程分析方法进行计算,其计算模型如图2所示。该方法较适合分析存在下卧刚性基岩场地条件的土-结构动力相互作用问题,通过设置考虑能量辐射效应的人工边界条件,同时也将自由场反应的影响作为一种力边界条件作用在截断边界上,是目前为止精度较高的土-结相互作用分析方法[21]。其中:场地土体两侧边界的弹簧系数、阻尼系数以及自由场等效节点力可参考文献[22]进行确定。

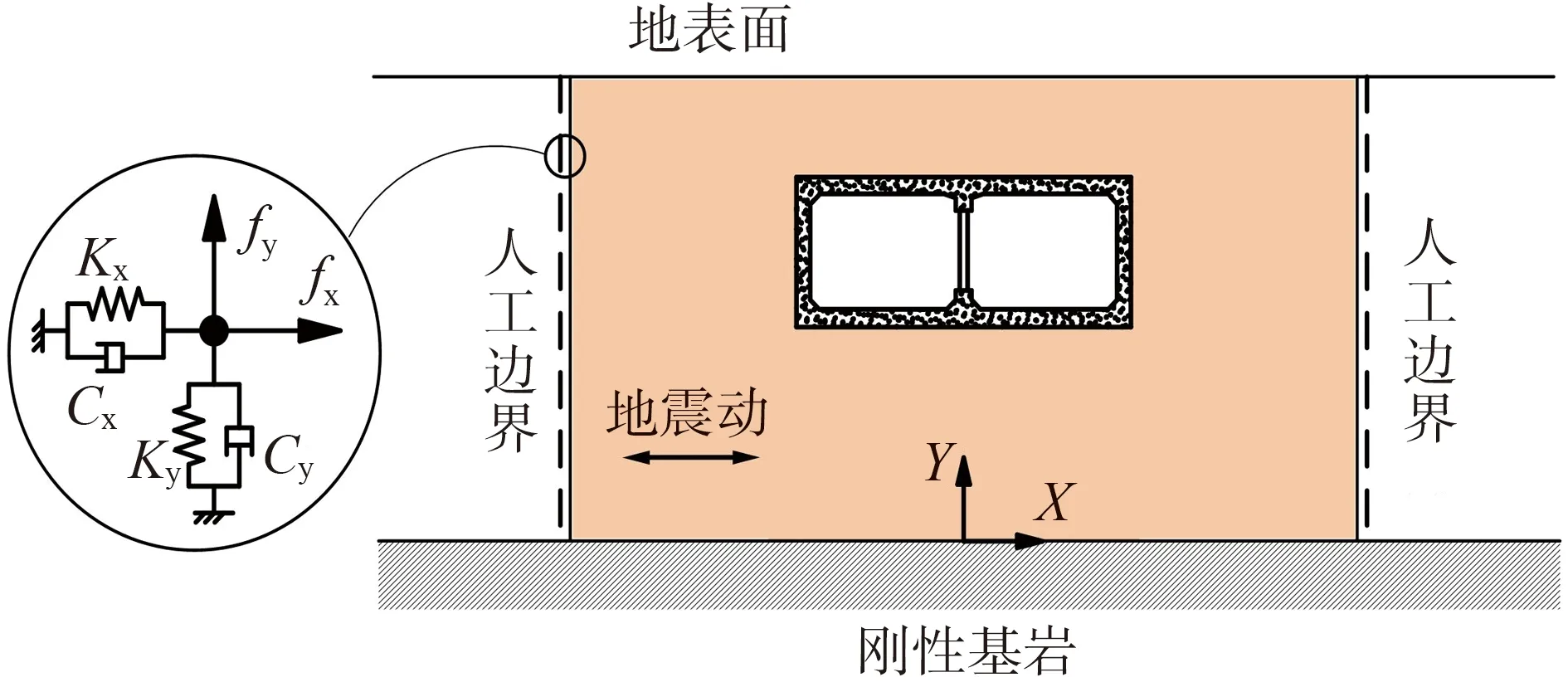
图2 动力时程分析方法计算模型Fig. 2 Calculation model of dynamic time-history analysis method

2 实例分析

2.1 工程概况

本节选取一典型单层双跨地下结构进行实例分析,该结构横断面的尺寸如图3所示,车站结构外轮廓尺寸为12.5 m×6.5 m,顶底板及侧墙厚度均为0.5 m,构件轴线尺寸为12 m×6 m。结构跨中设有矩形截面中柱,中柱的截面尺寸为1 m×0.4 m。且中柱在车站结构纵向为等间距分布,相邻中柱轴线间距为5 m。结构顶底板、左右侧墙和中柱的材料均选用C30型号混凝土。侧墙和顶底板的弹性模量取为30 GPa,由于该研究建立的是二维模型,中柱的弹性模量需按其纵向间距进行折减,折减后的弹性模量取为6 GPa。此外,该研究主要讨论弹性条件下地下结构的地震反应,故结构采用弹性模型且不考虑钢筋的作用。

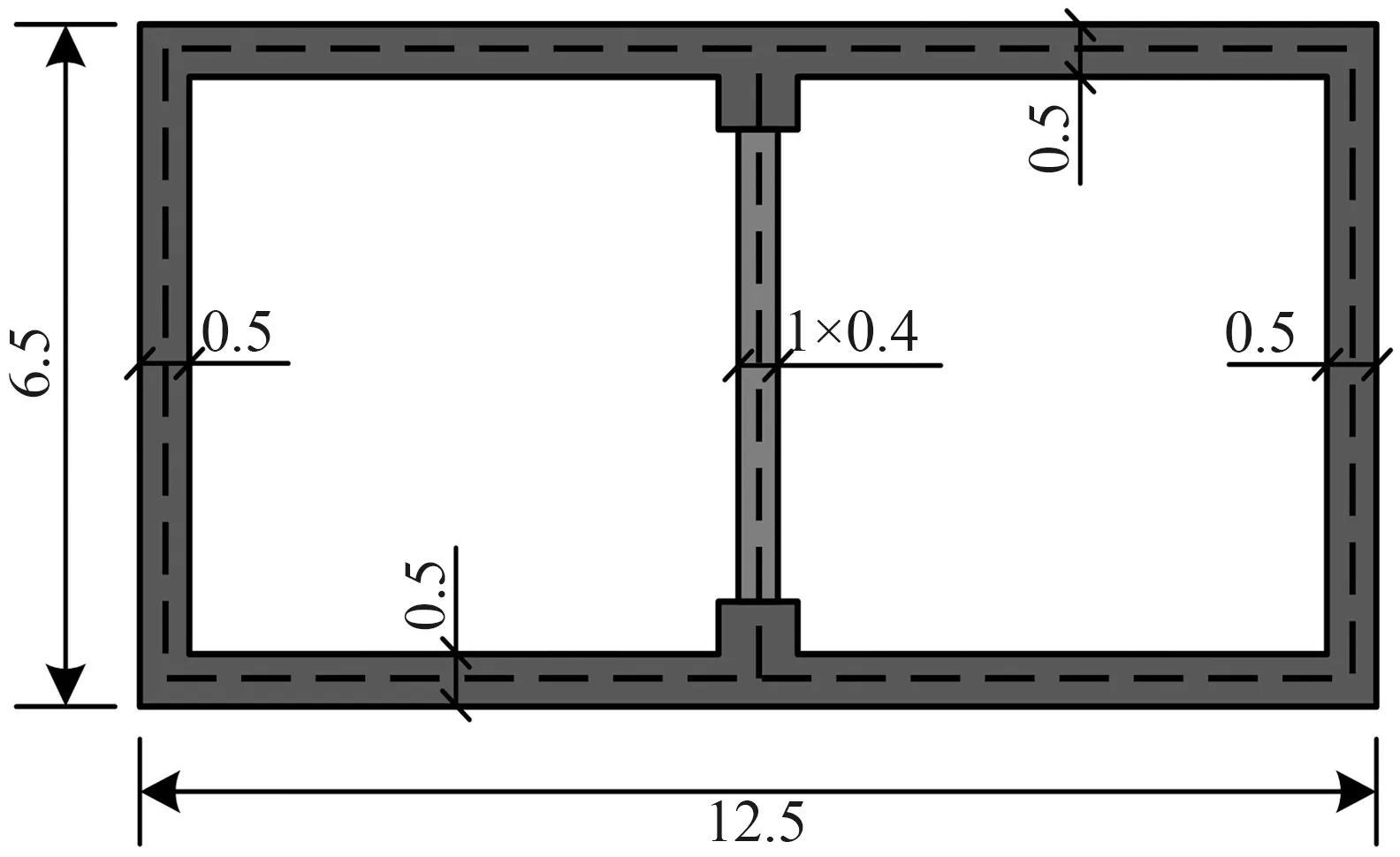
图3 地下结构横断面Fig. 3 Cross section of underground structure

场地土层共分为11层,土层表面至基岩面的垂直距离为40 m,场地土层表面至结构顶面的垂直距离为5 m。表1列出了进行场地地震反应分析所需要的土层剖面的土层分层厚度及土层土体性状描述资料,包括土体的土体的密度、剪切波速和泊松比等。在第4层时,通过改变土层剪切波速(由275 m/s调整为80 m/s),设置一软弱夹层场地。一般成层场地和软弱夹层场地的剪切波速图也列于表1。

表1 场地土层参数Table 1 Site soil parameters

输入地震动为Chi-Chi地震动和Duzce地震动,其加速度时程曲线如图4所示。计算时对该地震动记录的幅值进行调整,取峰值加速度为0.1 g。场地土体的阻尼特性通过瑞利阻尼考虑,瑞利阻尼系数α和β按下式计算:

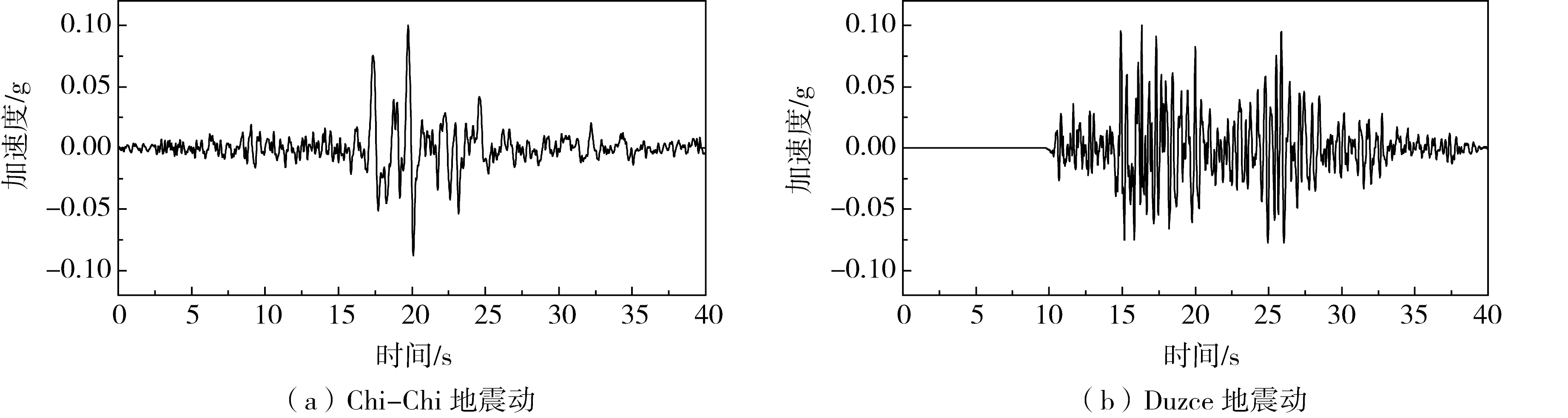
图4 地震动加速度时程曲线Fig. 4 Time history curves of ground motion acceleration

(2)

式中:ζn为第n个土层的阻尼比,这里近似假设各个土层的阻尼比为10%,ωi和ωj分别取为场地的第一阶自振频率和输入地震动的傅氏谱的卓越频率[23]。

2.2 有限元模型

基于ABAQUS软件建立一维场地地震反应分析、地基弹簧刚度系数求解、反应位移法求解以及动力时程分析的计算模型,如图5所示。在地基弹簧刚度系数和动力时程分析方法的计算模型中,场地土体的几何尺寸和网格大小保持一致,土体总宽度为84 m,为结构宽度的7倍;土体总高度为40 m;土体网格采用统一尺寸划分,大小为0.5 m×0.5 m。地下结构采用二维梁单元模拟,土体采用四节点平面应变单元模拟。结构顶板埋深10 m,结构中部设置一厚度为2m的软弱夹层。在一维场地地震反应分析模型中,土体底部固定,顶部自由,左右两侧设置水平滚轴边界。在地基弹簧刚度系数求解模型中,土体顶部自由,左右两侧和底部均固定。在反应位移法求解模型中:k表示地基弹簧刚度系数,下标T、R、B和L分别表示上顶板、右侧墙、下底板和左侧墙;下标1和2分别表示水平方向和竖直方向。在动力时程分析模型中,土体底部固定,顶部自由,左右两侧设置粘弹性人工边界条件。由图1所示的反应位移法计算模型可知:地下结构周边的地基弹簧既可受拉又可受压,为充分保证反应位移法与动力时程分析方法之间的可比性,结构和土体之间假定具有较好的粘结,即采用绑定接触。一维场地和土-结构体系的地震动输入方法均采用杜修力等[22]提出的振动法,认为此时场地底部下卧刚性基岩,地震荷载通过对土体和结构施加水平惯性力的方式实现,目前该方法已被验证具有良好的计算精度。

图5 有限元模型Fig. 5 Finite element models

通过一维场地地震反应分析确定结构顶底板位置土层出现最大相对位移的时刻,并将此时的土层相对位移、顶底板位置土层剪力和土层加速度提取出来,转换为地下结构所受的等效地震荷载。在动力时程分析时,则通过完整输入两条加速度时程曲线,获得地下结构的动力响应,并将最不利时刻结构的反应作为衡量不同工况下反应位移法计算结果的标准。

2.3 计算结果

一般成层场地中反应位移法和动力时程分析方法的计算如图6-7所示,其中:RDM表示反应位移法(response displacement method),THAM表示动力时程分析方法(time history analysis method)。对于两条不同的地震动而言,反应位移法和动力时程分析方法所计算的结构内力分布规律基本一致,反应位移法所计算的各个构件的内力总体上要比动力时程分析所计算的结果要小,尤其是在结构角部的时候,由于设置集中的地基弹簧无法准确反映土体对地下结构的约束条件,这与刘晶波等[24]的研究结论一致。

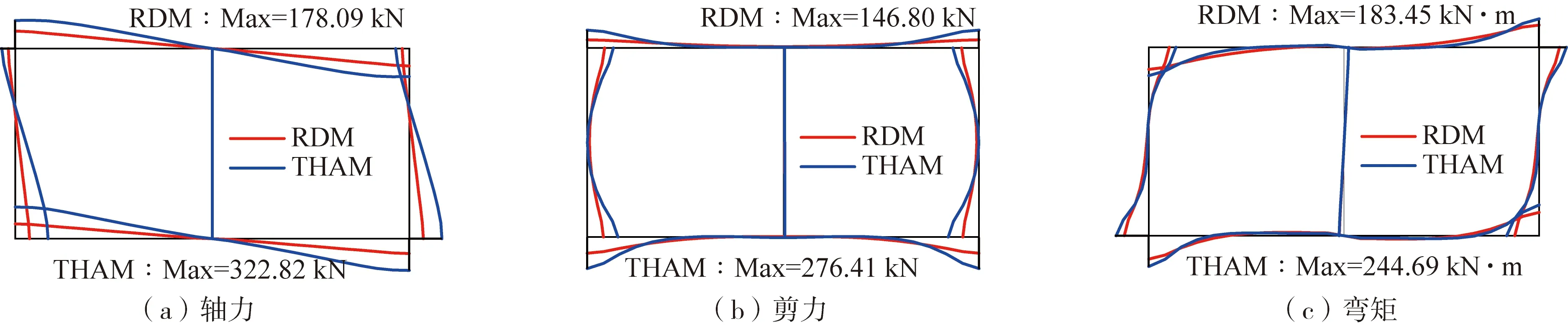
图7 Duzce地震动作用下一般成层场地结构内力图Fig. 7 Internal force diagram of structure in general layered site under Duzce earthquake

软弱夹层场地中反应位移法和动力时程分析方法的计算如图8-9所示。从图中可以看出:两条地震动作用下,在各个构件的轴力和弯矩图的变化趋势方面,反应位移法和动力时程分析方法基本一致,整体上,采用反应位移法计算的各个构件的轴力和弯矩要小于动力时程分析方法所计算的值。然而,与一般成层场地相比,侧墙位置处的剪力大小及分布存在显著区别。一般成层场地中,动力时程分析和反应位移法的计算结果均表明侧墙中部的剪力值最小,侧墙顶部和底部的剪力值较大,两种方法所得的剪力分布规律基本一致,表明反应位移法此时有较好的适用性。而在软弱夹层场地中,采用反应位移法计算出的侧墙剪力值沿高度方向变化不大,这与真实情况有显著区别。当地下结构穿过软弱夹层时,左右侧墙的剪力分布呈现“W”形状,在软弱夹层位置侧墙的剪力值最大,这是与一般成层场地最不同的地方,然而此时采用反应位移法则无法体现侧墙的这一受力特点。

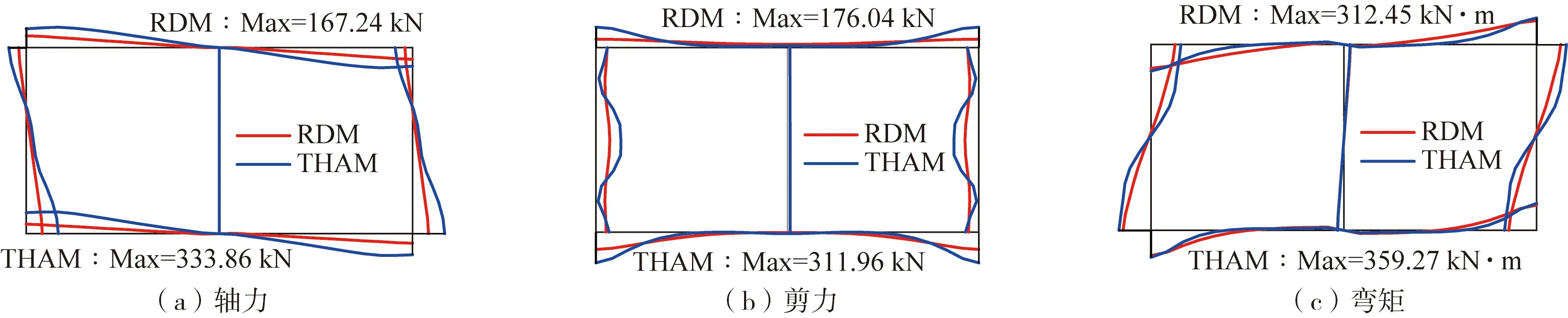
图8 Chi-Chi地震动作用下软弱夹层场地结构内力图Fig. 8 Internal force diagram of structure in site with weak interlayer under Chi-Chi earthquake

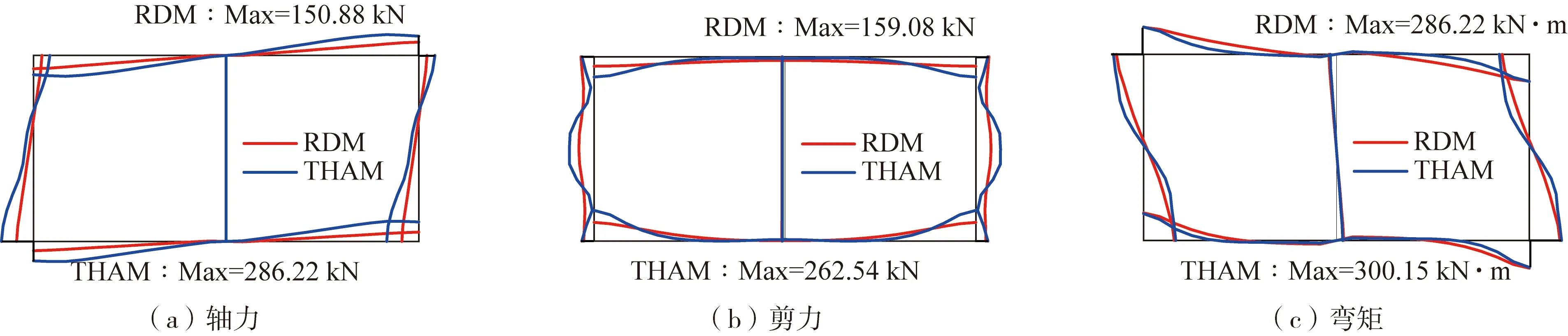
图9 Duzce地震动作用下软弱夹层场地结构内力图Fig. 9 Internal force diagram of structure in site with weak interlayer under Duzce earthquake

表2进一步给出了左侧墙剪力的误差统计分析,顶、中和底节点误差可通过下式计算:

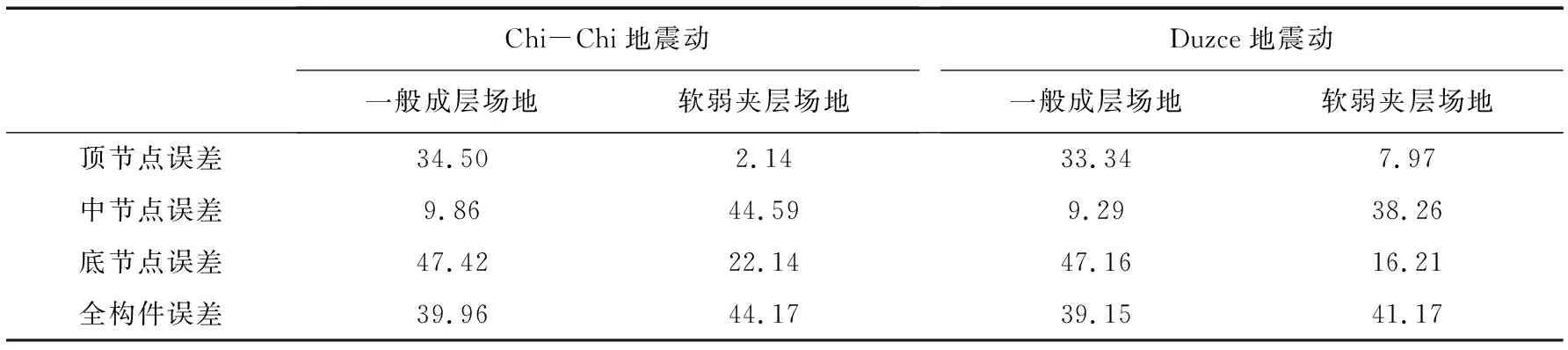
表2 左侧墙剪力误差统计(不同场地)Table 2 Error statistics of shear force of left wall (different sites) %

(3)

式中:FT表示动力时程分析方法所计算的侧墙顶节点、中节点或底节点的剪力值,FR表示反应位移法所计算的侧墙顶节点、中节点或底节点的剪力值。

显然,只通过顶部、中部和底部三个节点评价反应位移法计算误差不够完善。为了反映侧墙上各个节点剪力值的综合误差,表2也给出了全构件误差,其可通过下式计算:

(4)

式中:FTi表示动力时程分析方法所计算的侧墙第i个节点的剪力值,FRi表示反应位移法所计算的侧墙第i个节点的剪力值,n为侧墙节点的总数。

由表2和不同场地中侧墙的剪力图可知:尽管在侧墙顶部和底部位置,软弱夹层场地中反应位移法的计算误差更小,但此时侧墙顶部和底部的剪力值并不是整个构件的峰值,也就是说侧墙剪力的控制截面不在两端而在中间。由全构件误差分析可知:较一般成层场地而言,软弱夹层场地中应用反应位移法所计算的结果误差更大,即适用性降低。

3 误差分析

3.1 地基弹簧

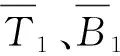
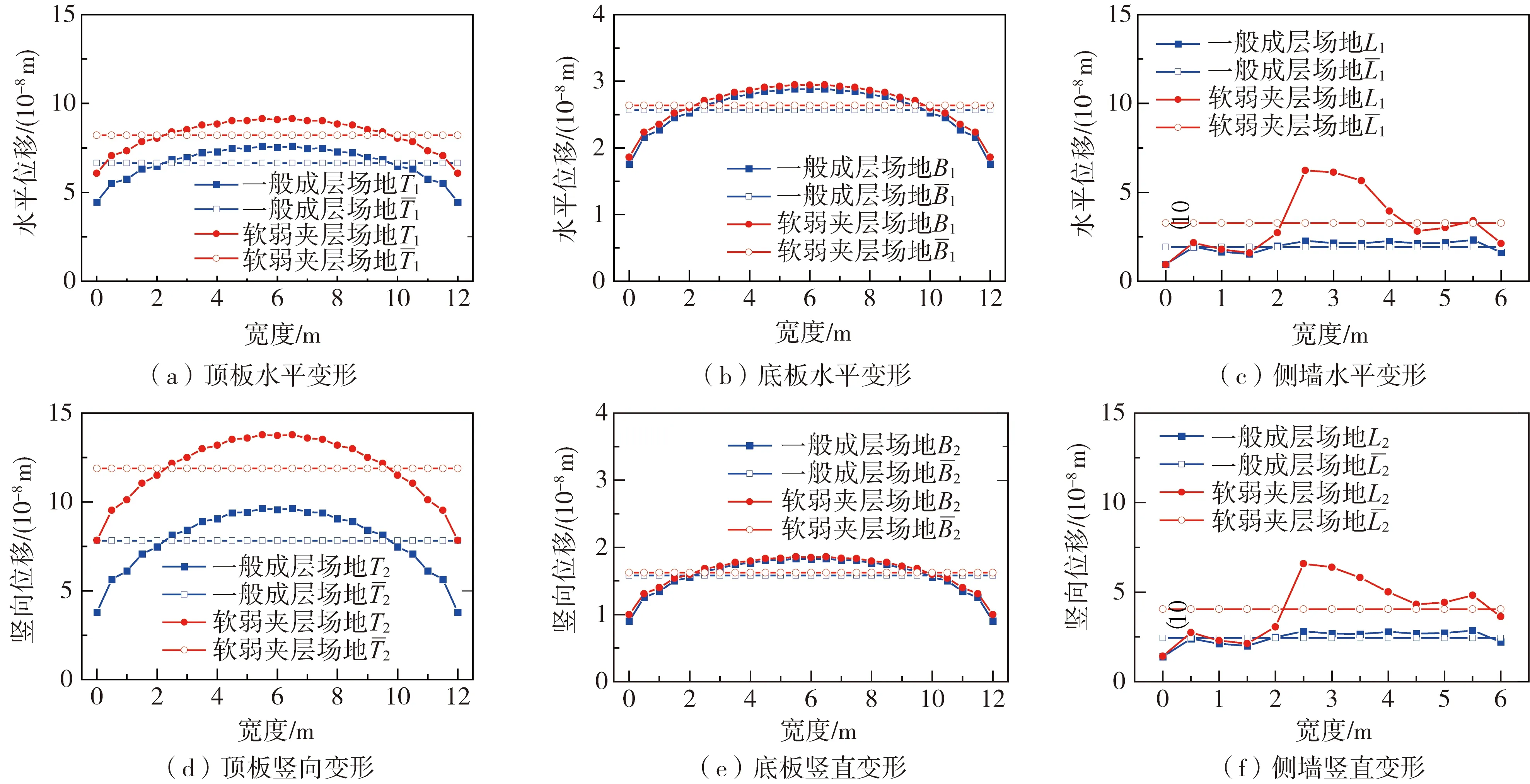
图10 单位荷载下孔洞节点变形Fig. 10 Deformation of hole nodes under unit load

为进一步说明地基弹簧对反应位移法计算结果的误差,本节继续对比由土层相对位移引起的等效地震荷载。这是由于在反应位移法中,通常将土层相对位移乘以对应位置的地基弹簧刚度系数换算为等效节点荷载,这实际上是一种近似解。要求出由土层相对位移引起的等效地震荷载的精确解可以借鉴刘晶波等[25]提出的整体式反应位移法,即在图5所示的地基弹簧系数求解模型中,对孔洞各个节点施加由一维土层地震反应分析获得的土层相对位移,进而提取孔洞各个节点在水平和竖向的反力,即为由土层相对位移引起的等效地震荷载。取地下结构顶底板位置处相对位移最大时作为最不利时刻,此时一维场地的水平变形如图11所示,从图中也可以看出:场地的水平位移在软弱夹层位置发生较大的突变。进一步获得由土层相对位移引起的等效地震荷载,其对比结果如图12所示。由式(1)可知:传统反应位移法只能计算结构外圈节点上由土层相对位移引起的水平等效地震荷载,竖向等效地震荷载为0。另外,底板位置相对位移为0,引起的水平等效地震荷载也为0,侧墙位置的水平等效地震荷载沿着高度方向逐渐增大,而顶板位置相对位移和地基弹簧刚度是一致的,故侧墙位置的水平等效地震荷载大小不变。然而,通过图所示的模型所求解的等效地震荷载与式(1)所求解的近似解存在显著差别:其一体现在计算结构外圈节点的竖向等效地震荷载;其二体现在软弱夹层位置处的水平向等效地震荷载。很明显,软弱夹层位置处的水平向等效地震荷载接近于0,此时仍认为侧墙处的地基弹簧刚度系数一致,则会显著高估软弱夹层位置处侧墙所受的水平向等效地震荷载。也就是说,采用集中的地基弹簧模拟土体对地下结构的约束作用时,地基弹簧彼此独立,无论是弹簧对地下结构的约束,还是弹簧与土层相对位移共同确定的地下结构所受的等效地震荷载,都与真实情况不符。

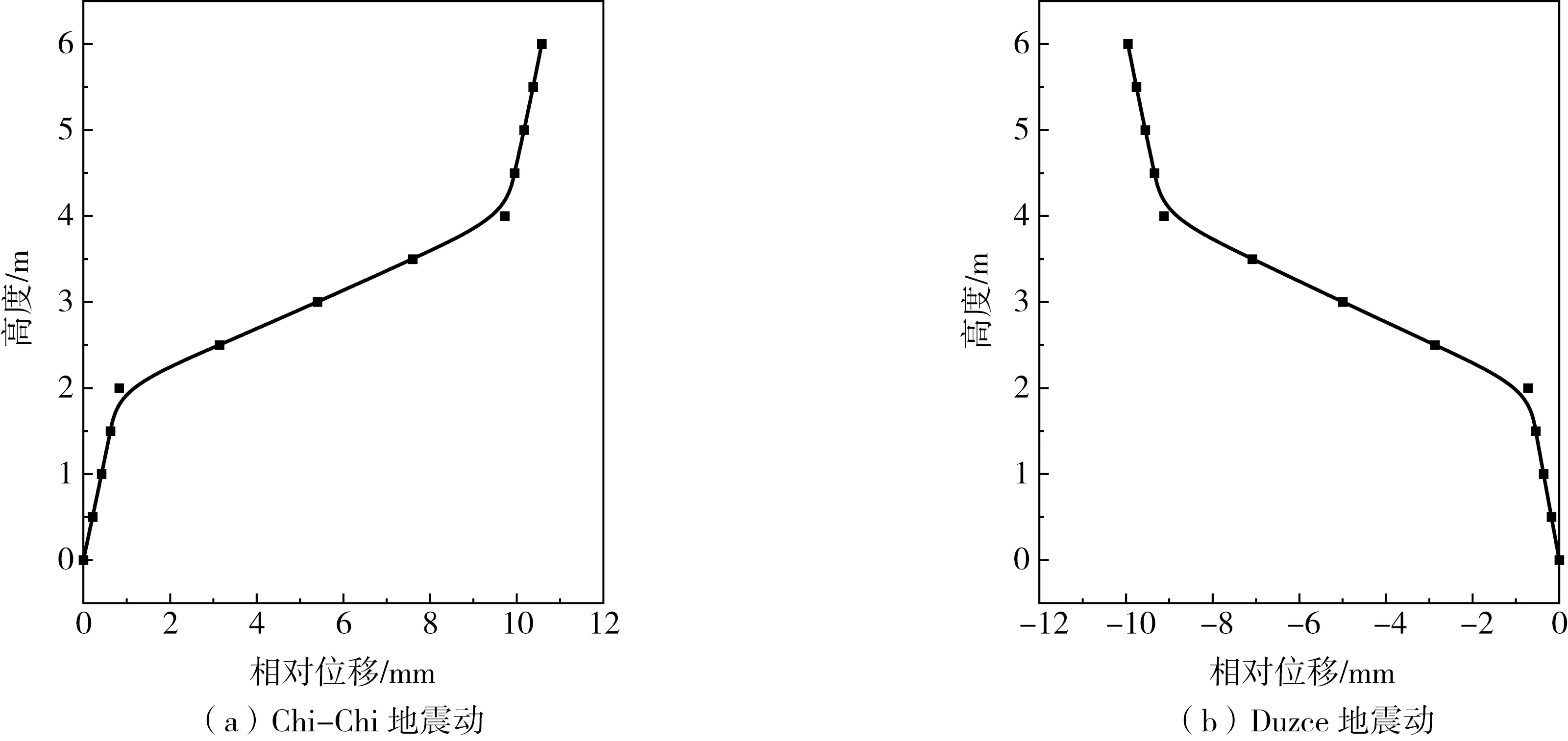
图11 由场相对位移Fig. 11 Relative displacement of free field

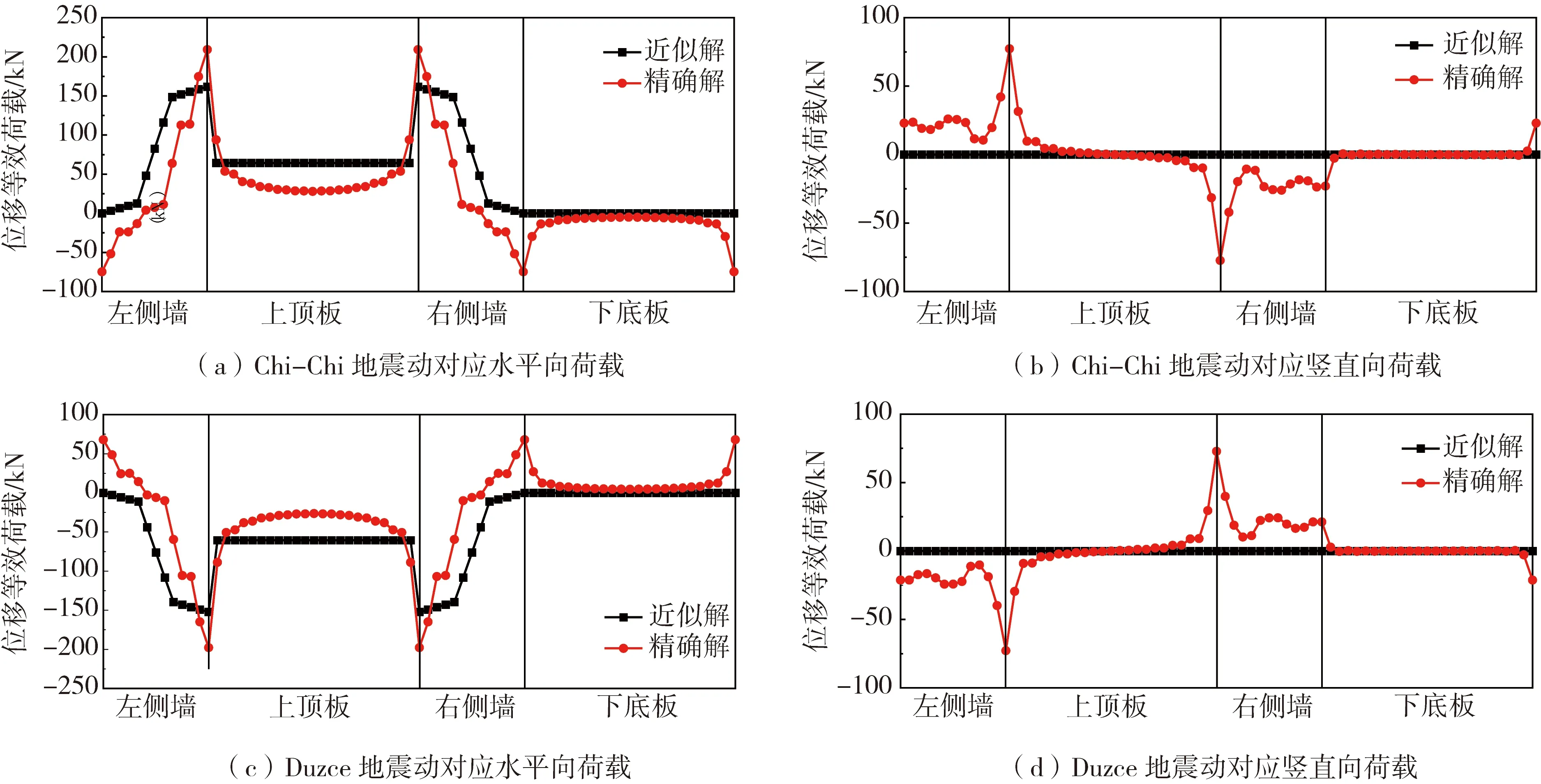
图12 土层相对位移引起的等效荷载Fig. 12 Equivalent load caused by relative displacement of soil

3.2 土层剪力

地下结构周边的土层剪力是反应位移法中的另一重要参数,也是地震作用下地下结构所受的重要荷载组成。规范中对于反应位移法中剪力部分的规定较为简单,矩形结构顶底部分剪力取对应位置处土层剪力,结构左右侧墙位置土层剪力取顶底剪力的平均值。图13给出了结构位置处土层剪力。从图中可以看出:土层剪力沿车站高度方向大致呈现线性分布。当侧墙位置的土层剪力取顶底板位置土层剪力的平均值时,与真实土层剪力分布相差并不大,最大相差不到20%。

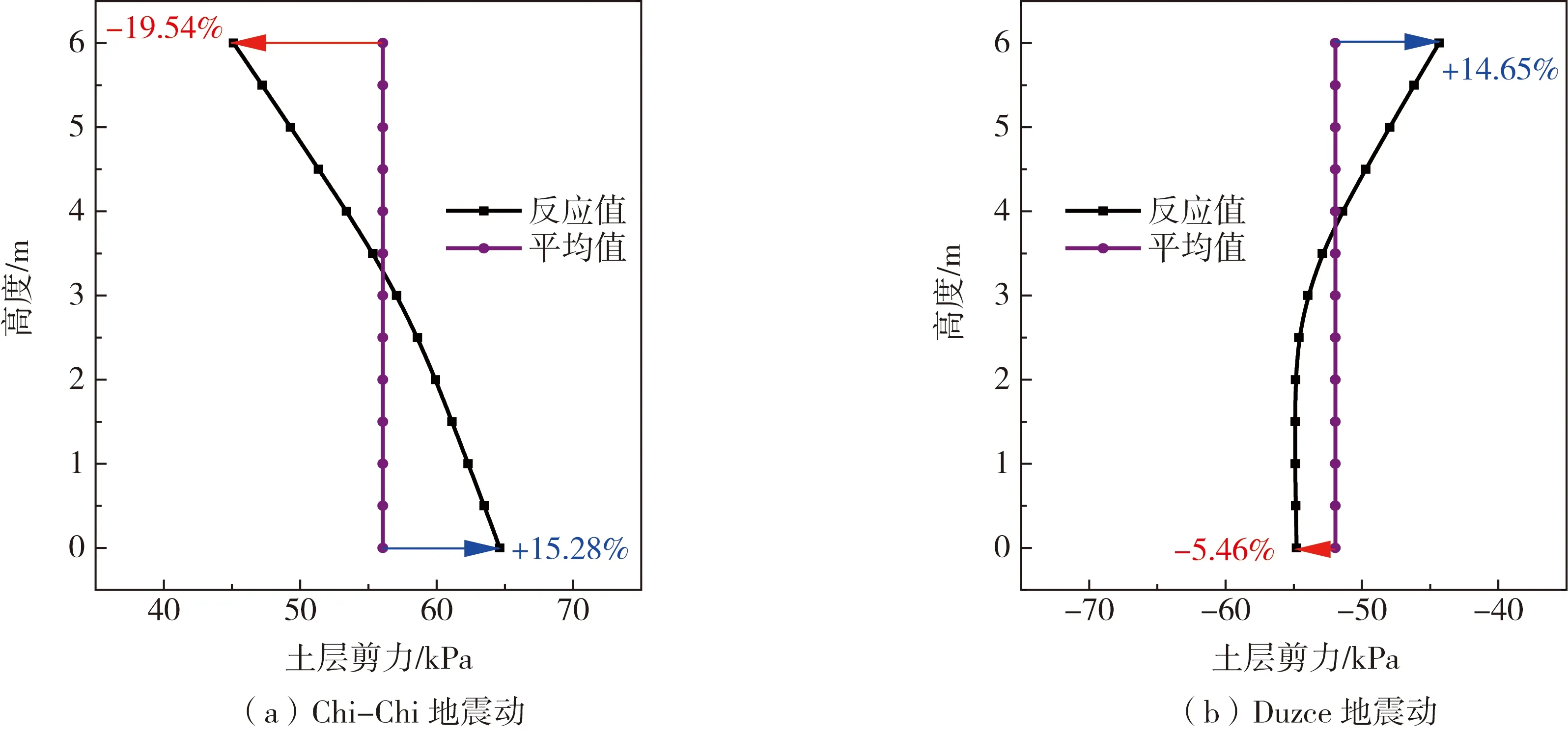
图13 结构位置处土层剪力Fig. 13 Soil shear force at structure location

3.3 结构惯性力

反应位移法除了考虑土层相对位移和土层剪力引起的等效地震荷载以外,还考虑了地震作用下地下结构自身的惯性效应。然而,有研究表明:地下结构自身惯性效应对其地震反应贡献较小。图14给出了结构位置处土层水平加速度沿高度分布情况。从图中可以看出:在软弱夹层位置处,土层的水平加速度存在突变。考虑当地下结构自身惯性效应不明显的原因,因此认为该部分引起的计算误差不大。

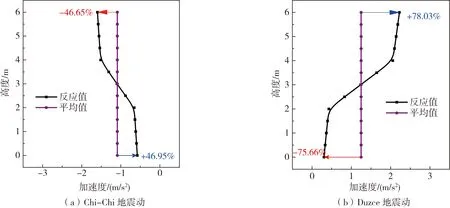
图14 结构位置处土层水平加速度Fig. 14 Horizontal acceleration of soil at structure location

4 整体式反应位移法应用

为克服上述计算误差,本节采用刘晶波等[25]提出的整体式反应位移法计算了上述软弱夹层场地地下结构的地震反应,其与动力时程分析方法计算结果对比如图15所示。需要说明的是:在该研究的整体式反应位移法中,土层剪力和结构惯性力都与反应位移法中的荷载一致,不同之处仅体现在地基弹簧以及由土层相对位移引起的等效地震荷载。从图15中可以看出:整体式反应位移法和动力时程分析方法所确定的结构内力大小和分布规律基本一致。表3进一步给出了整体式反应位移法的误差分析,综合对比表2和表3可以看出:整体式反应位移法基本上可以准确得出侧墙各个节点的剪力值,各类误差均在在10%以内。也就是说,整体式反应位移法的计算精度大幅提升,适合应用于含软弱夹层场地中地下结构的抗震分析。

表3 左侧墙剪力误差统计(不同方法)Table 3 Error statistics of shear force of left wall (different methods) %

进一步分析表3也可以得出:当采用整体式反应位移法时,改变了地基弹簧和土层相对位移引起的等效地震荷载,此时简化分析方法就可获得精度较好的计算结果。这与第三节的分析结果一致,土层剪力和结构惯性力的简化处理所引起的计算误差并不大。也就是说,对于软弱夹层场地,不可简单按式(1)由土层相对位移引起的等效地震荷载,而应按照整体式反应位移法推荐的方法确定该部分等效荷载,并进一步采用土-地下结构整体分析模型进行静力计算,即可获得与动力时程分析方法相近的计算结果。