含子盆地的二维沉积盆地非线性地震反应分析

陈树培,温卫平,翟长海,白克生

(1. 哈尔滨工业大学 结构工程灾变与控制教育部重点实验室,黑龙江 哈尔滨 150090;2. 哈尔滨工业大学 土木工程智能防灾减灾工业与信息化部重点实验室,黑龙江 哈尔滨 150090)

0 引言

沉积盆地内部地势平坦,自然条件良好,如成都等许多重要城市均建立在盆地内部。然而,地震作用下,沉积盆地会表现出明显的盆地效应,加重地震破坏[1]。因此,研究沉积盆地地震反应对这些城市抗震设防具有重要意义。盆地效应主要表现为边缘效应、聚焦效应及共振效应[2],相比于水平成层场地,上述效应的综合作用导致盆地地形产生了额外的放大作用。因此,盆地效应受到了研究者的广泛关注。然而,当前研究多专注于未包含子盆地的普通盆地[3-6],在沉积盆地中,由于地表河流和湖泊等的长期沉积作用,容易在盆地内形成新的沉积盆地。子盆地形成年代较晚,其土体物理性质和周围土体有很大差别。KAWASE等[7]基于数值模拟方法,研究了1985年墨西哥地震中墨西哥城的强地面运动特征,并指出子盆地结构是墨西哥城地震动“强幅值和长持时”特征的重要原因之一;AOI等[8]通过分析含子盆地结构的Yufutsu盆地地震反应,支撑了这一观点;GRAVES[9]基于三维数值模型研究了洛杉矶盆地的地震反应,结果表明盆地-子盆地的组合模型能更好地解释洛杉矶盆地的地震反应,子盆地的影响不可忽略;NARAYAN等[10]研究了二维盆地-子盆地地震反应,讨论了外围大盆地对子盆地共振模式的影响,研究表明:外围大盆地降低了子盆地的基频,子盆地依旧出现了共振现象;刘昇等[11]采用谱元法,研究了盆地形状比对盆地-子盆地模型共振效应及盆地放大系数的影响。上述研究表明:盆地-子盆地这容易特殊地质构造对地震动有放大作用,采用单一的盆地构造进行场地反映分析将低估地表地震反应。然而,现有研究多针对特定的盆地-子盆地构造,子盆地尺寸、介质波速、子盆地与盆地相对位置等因素对盆地-子盆地地震反应的影响尚不清晰。为综合评估子盆地与外围大盆地间的相互作用对沉积盆地地震反应的影响,本文基于有限元数值方法,综合考虑子盆地的尺寸、盆地-子盆地相对位置、子盆地介质波速以及盆地倾角等因素的影响,研究了盆地-子盆地地震反应特征及其对地震动的影响。

1 数值模拟方法

1.1 有限元模型

本文采用理想化的二维梯形盆地模型,模型长5000 m,深700 m。梯形盆地表面宽2000 m,深度100 m,倾角为α,盆地与左右两侧边界距离取为1500 m。由于子盆地尺寸较小,用梯形模拟具有较大的误差,本文参考文献[10-11]的子盆地形状,采用曲边的椭圆形状建立子盆地模型。此外,本文中子盆地深度固定为50 m,子盆地形状比变化由改变子盆地宽度表征。模型示意图如图1所示。

图1 计算模型示意图Fig. 1 Diagram of the numerical model

计算完成后,选取盆地表面共103个节点的水平分量速度时程(本文所有结果速度和加速度均取水平分量)作为观测结果进行分析研究,由于盆地外围基岩处计算结果接近,仅在盆地左右两侧取包含盆地表面与基岩交界点的两个观测点,重点分析盆地内部的地震反应差异。盆地内部观测点间距为20 m,选取共103个节点的水平分量速度时程(本文所有结果速度和加速度均取水平分量)作为观测结果进行分析研究。其中:盆地中心处观测点编号为52。由于篇幅限制,图2并未列出所有观测点的位置,仅列举了盆地左侧部分观测点,观测点分布如图2所示。

图2 盆地表面左半侧观测点分布Fig. 2 Distribution of observation points on the left half of basin

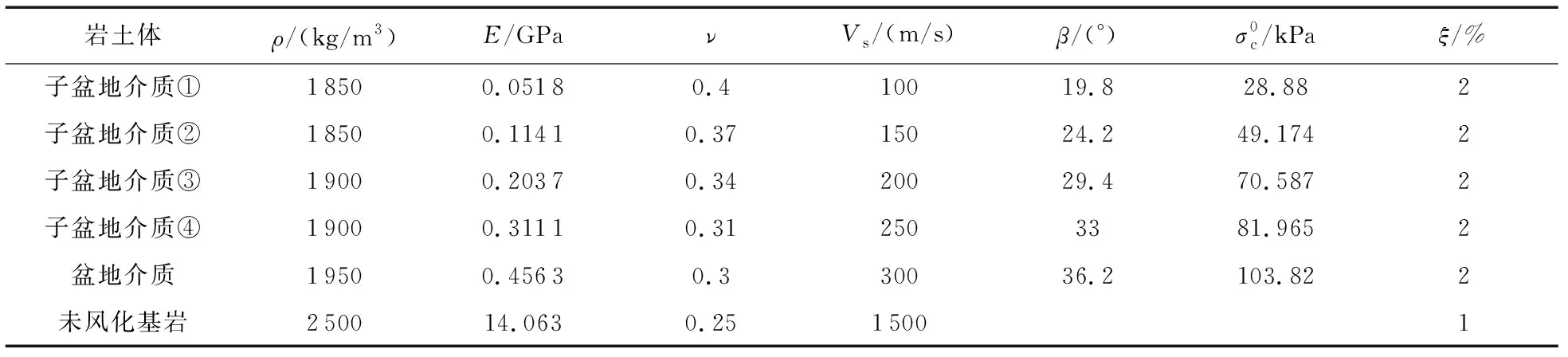
表1 岩土物理参数表Table 1 Physical parameters of the soils

图3 子盆地及其附近网格划分Fig. 3 Numerical meshes of the sub-basin and its adjacent area

1.2 地震动输入

本文地震动输入采用垂直基底入射的Kobe波,截取其5%～95%Arias烈度段(即其重要持时)段作为最终的输入,处理后的输入地震动时程及频谱信息如所图4所示。地震动输入时,采用波动法[15],将输入地震动速度时程换算为等效节点力施加于边界节点上。

图4 输入地震动时程与傅里叶谱Fig. 4 Time history and Fourier spectrum of the input motion

1.3 工况设定

本文针对沉积盆地中子盆地的尺寸、子盆地在盆地中的位置、子盆地沉积物的剪切波速以及盆地倾角对盆地地震反应的影响,包括不含子盆地的一个工况,共设置了13种工况,详见表2。本文各工况以wiaiVsipi的格式命名。其中:w表示子盆地宽度,a表示外围盆地倾角,Vs表示子盆地介质波速,p表示子盆地在盆地中的位置,为子盆地左侧边缘距沉积盆地左侧边缘距离。在本文子盆地深度取为50 m不变,通过改变子盆地表面宽度来表征子盆地尺寸变化,宽度分别取100、200、300和400 m;盆地倾角分别取30°、45°和60°;子盆地介质波速分别取100、150、200、250 m/s;当研究子盆地在沉积盆地中不同位置的影响时,保持盆地倾角45°和子盆地表面宽度200 m不变,以子盆地左侧边缘距沉积盆地左侧边缘100、360、630和900 m设定子盆地位置。此外,由于盆地倾角不同引起的盆地边缘长度变化,盆地倾角为30°时,p1=173 m;当倾角为45°时,p1=100 m;当倾角为60°时,p1=58 m。

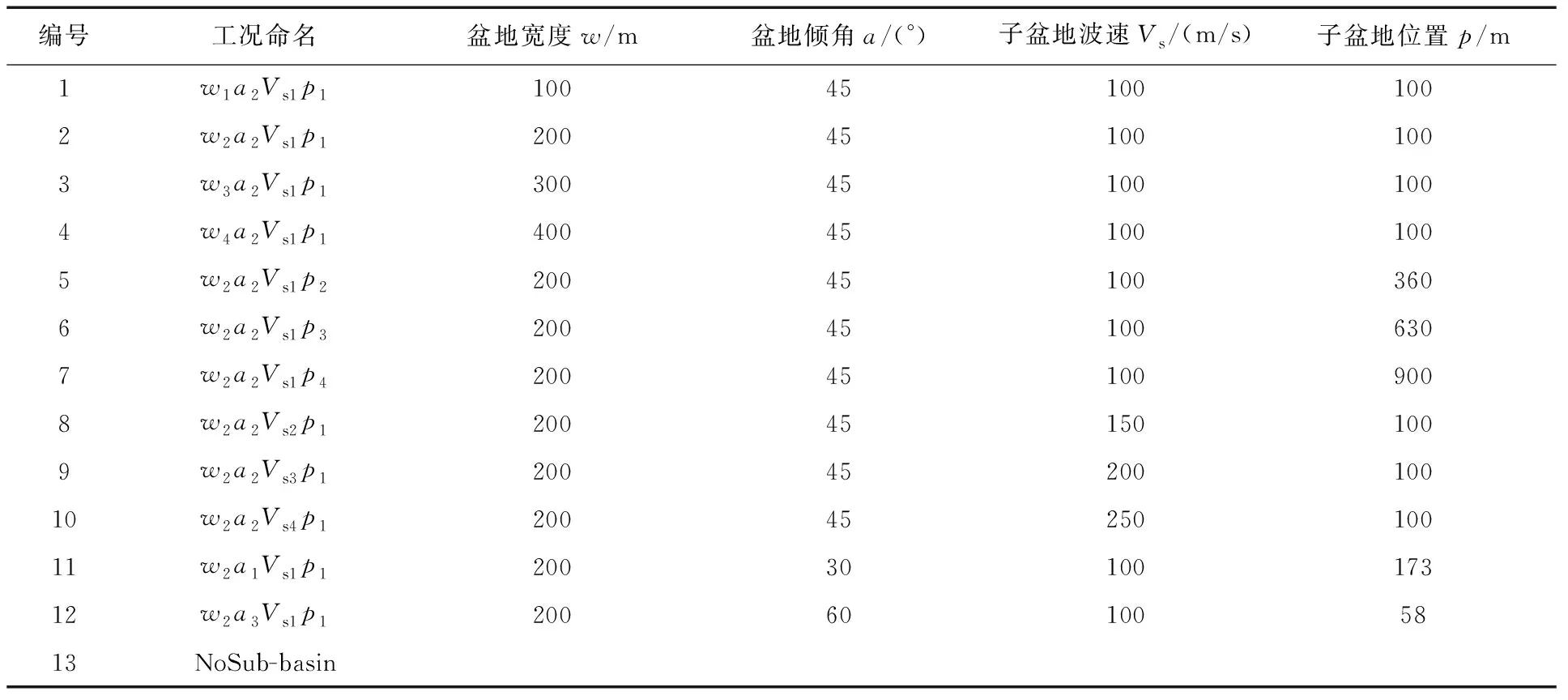
表2 子盆地计算工况表Table 2 Calculation cases of the sub-basin

2 模拟结果分析

2.1 子盆地对盆地地震动场分布的影响

为了能更加直观和清晰的观察子盆地的存在对沉积盆地的地震动场分布的影响规律,本节选取w2a2Vs1p1为典型工况,对比不含子盆地的工况,研究盆地地震动场分布时空差异性。其速度波场与PGA分布见图5。此处应当说明:由于沉积盆地外围基岩的地震反应几乎一致,因此图5中仅给出了观测点1～103处的结果,即距盆地中心±1040 m范围内的计算结果。

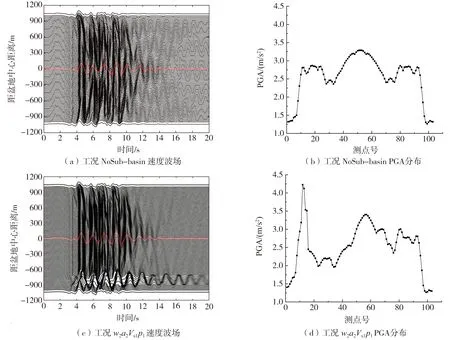
图5 工况w2a2Vs1p1与NoSub-basin的速度波场和PGA分布Fig. 5 Velocity wave fields and PGA distributions of case w2a2Vs1p1与NoSub-basin.

由图5(a)可以看出:盆地边缘产生了较为明显的次生面波,并从盆地两侧边缘向中间传播,传播过程清晰可见,子盆地的存在对面波在盆地表面的传播产生了很大的影响。首先,经过子盆地的面波相比没有子盆地存在的一侧有明显的迟滞,使得从两侧向中心传播的面波相遇发生干涉的位置向含子盆地的一侧偏移;经过子盆地后的面波幅值有所下降;由于子盆地和周围土体的波速相差较大,故到达子盆地的体波在子盆地边缘同样产生了次生面波,使得盆地表面面波的传播变得更加复杂。在盆地的中央区域,可以清晰的看到在盆地基底与表面之间的多次反射波,以及从盆地两侧边缘传递来的次生面波在盆地中央相遇发生相长干涉而形成的波动,使得速度时程出现一个较大的起伏。

从图5(b)盆地表面PGA的分布图可以看出在无子盆地的边缘区域存在明显的边缘效应,而另一侧边缘处存在的子盆地对从基底传递到盆地表面的体波有明显的聚焦作用,使得子盆地中心(观测点12)的地震反应出现了剧烈增强,其PGA幅值明显大于无子盆地模型,同时由于子盆地的存在对地震波的散射作用,在子盆地左右外侧附近的地震反应有一定的削弱;此外,子盆地还将“捕获”一部分传播至子盆地中的次生面波,使其难以向盆地中心继续传播,也将一定程度上削弱子盆地附近的地震动;随着向盆地中心靠近,子盆地模型地表PGA逐渐趋于盆地模型,子盆地对地震动的影响逐渐降低。

图6给出了盆地中心处与子盆地中心处的传递函数。由图6(a)可知:工况NoSub-basin中心处共振频率约为0.7 Hz左右,接近于对应的一维土层自振频率Vs/4H= 0.75 Hz。此外,工况NoSub-basin中心在1 Hz处也出现了共振,但子盆地的存在削弱了该共振峰的峰值。该现象表明:盆地边缘产生的次生面波引发了新的盆地共振模式,且子盆地的存在将削弱往盆地中心传播的面波,进而削弱该共振模式。图6(b)给出了子盆地中心处(观测点12)工况NoSub-basin与w2a2Vs1p1的传递函数。由图可见:子盆地的聚焦效应放大了0.8 Hz、1 Hz与2 Hz处的地震反应,但子盆地区域对应的一维土层自振频率Vs/4 Hz = 0.5 Hz,这表明工况w2a2Vs1p1的共振模式以盆地的二维共振为主。

2.2 子盆地尺寸对盆地地震反应的影响

本节重点关注盆地地表PGA分布情况,对比分析子盆地的尺寸对盆地地震反应的影响。为了分析子盆地的存在对盆地地震动响应的影响,用不含子盆地的PGA做归一化处理,即定义PGA放大系数为含子盆地

的地表PGA与对应观测点不含子盆地PGA的比值,下文中的PGA放大系数与此相同。当放大系数大于1时,说明子盆地的存在对盆地地表地震动有放大作用,反之则具有削弱作用。本节重点分析包括不含子盆地工况在内的5个工况,详细计算参数见表3。各工况PGA放大系数分布见图7。

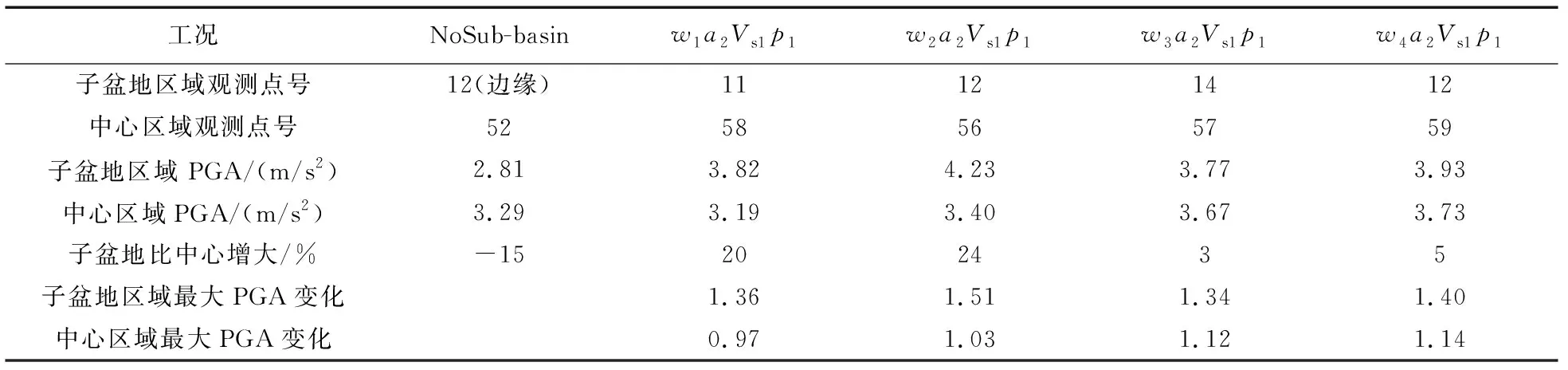
表3 工况1、2、3、4盆地中心与子盆地区域对应的观测点号、PGA及其放大系数Table 3 Observation point number, PGA and amplification factor corresponding to the centre area and the sub-basin area in cases 1 ,2, 3, and 4

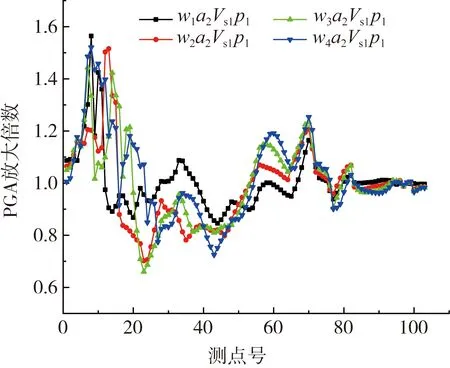
图7 工况1、2、3和4的沉积盆地地表PGA放大系数分布Fig. 7 PGA amplification factor distributions of cases 1 ,2, 3, and 4

由图7可见:

1)子盆地中的PGA放大系数几乎是整个盆地中最大的,这是由于子盆地聚焦效应导致了地震动的剧烈增强,在观测点8处,子盆地宽度为100 m时,PGA被放大了近1.56倍;随着子盆地尺寸增大,子盆地区域的PGA分布出现分化,形成一左一右两个幅值,左侧幅值稍大些(工况3和4),这是因为本文中设定子盆地深度不变,而通过增加子盆地表面宽度来增大子盆地尺寸,随着子盆地表面宽度增加,基底传递来的地震波不再能聚焦于子盆地中心,且由于盆地左侧面波的影响,使得左边的幅值稍大。

2)子盆地的存在对整个盆地的PGA及其放大系数的分布具有很大的影响,相比NoSub-basin工况,除远离子盆地的右侧边缘区域,沉积盆地大部分区域的PGA分布发生了明显改变;在子盆地外右侧区域(观测点20～50)出现PGA被抑制的现象,放大系数小于1,在观测点23处,子盆地宽度为300 m时,PGA仅为不含子盆地的0.66倍,这是由于从盆地左侧边缘激发传播来的面波经过子盆地后强度被削弱,导致与基底直达体波相遇发生干涉的强度减小;在盆地中央区域,从NoSub-basin工况可以看出沉积盆地中央区域的PGA峰值要大于盆地边缘处的PGA峰值,说明盆地中央垂直向一维共振(提取得到盆地基频为0.727 Hz,和输入地震动Kobe波傅立叶谱最大峰值处频率0.732 Hz接近)对地震动的放大要大于盆地边缘效应对地震动的放大。随着子盆地尺寸增加,沉积盆地中央区域PGA分布曲线收拢突起的现象越来越明显,PGA分布的峰值点逐渐增大并向盆地右侧移动,这是由于子盆地的存在导致一维共振中心向右偏移,子盆地尺寸增加进一步使其向右略微移动(移动距离较小,共振强度几乎不变),面波和体波相遇的区域逐渐向盆地右侧偏移,且由于传播路径缩短,面波衰减的幅度减小,导致峰值点略微增加。与NoSub-basin工况相比,随着子盆地尺寸增加,两者的差距变大,尤其是在子盆地区域和盆地中央偏右区域。

为更好地表明子盆地对盆地PGA分布的影响,对比了不同尺寸子盆地对盆地不同区域最大PGA的影响。由于不同工况的最大PGA出现的位置不同,此处以子盆地区域PGA最大值所在的观测点代表子盆地区域,以盆地中央PGA峰值所在的观测点代表中心区域,对比不同工况下盆地不同区域的最大PGA变化规律。以工况w1a2Vs1p1为例,该工况下中心区域最大PGA出现在58号观测点处,而NoSub-basin工况则出现在52号观测点处,则子盆地引起的中心区域最大PGA变化为以上两点PGA之比。各个工况子盆地、中心区域的PGA及其放大系数见表3,绘制两处区域的地表最大PGA及最大PGA变化随子盆地尺寸变化曲线如图8所示。

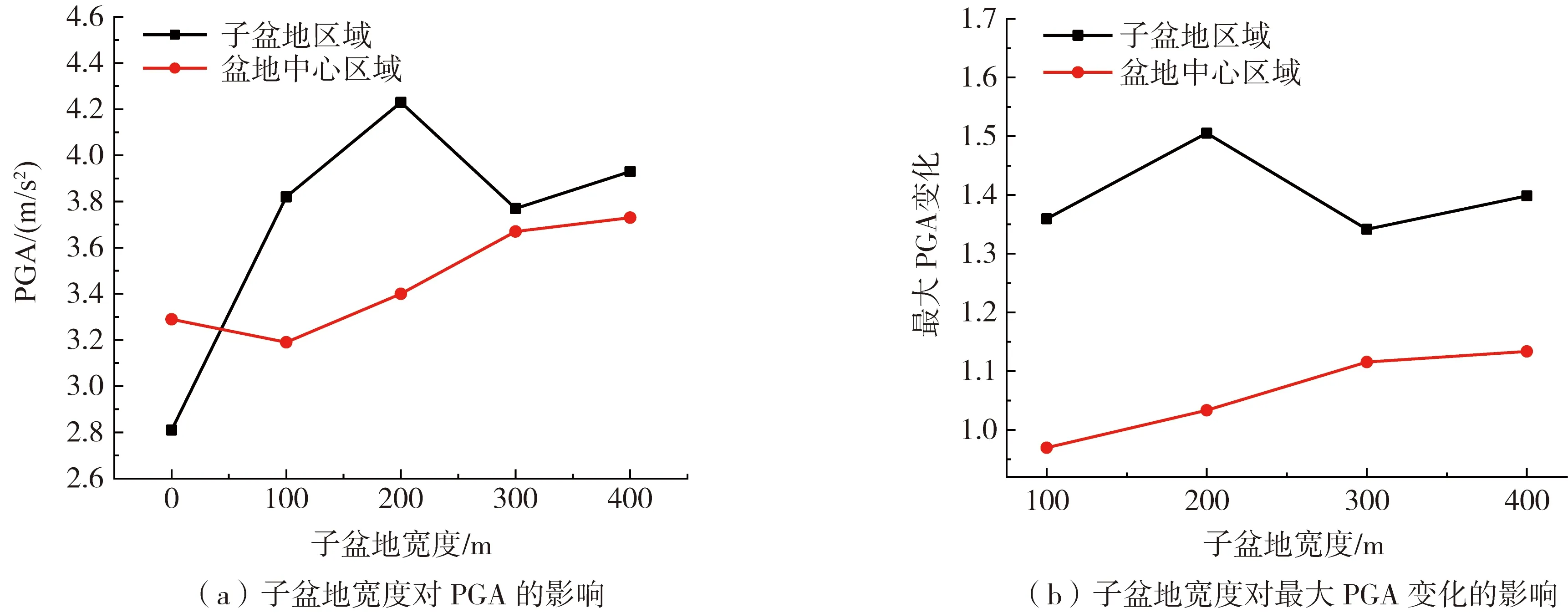
图8 子盆地尺寸对两处区域PGA及其放大系数的影响Fig. 8 Influence of the sub-basin size on the PGA maximum of basin edge and central area

从图8中可以看出随着子盆地尺寸的增加,子盆地区域的PGA及最大PGA变化先增大再减小的趋势,且放大系数均大于1;盆地中心区域的PGA及最大PGA变化则一直增大,只有在子盆地表面宽度为100 m时PGA略小于无子盆地的沉积盆地。子盆地区域PGA最大值(w2a2Vs1p1)比最小值(w3a2Vs1p1)大了约12%,盆地中心区域PGA最大值(w4a2Vs1p1)比最小值(w1a2Vs1p1)大了约17%;同一工况下,由于子盆地聚焦效应,在子盆地中心区域,其PGA比沉积盆地其他区域的大,由表3可知:工况w2a2Vs1p1中,子盆地区域PGA比沉积盆地中央区域增大的幅度最大,达到了24%左右。最大PGA变化随子盆地尺寸变化产生的先增大再减小的趋势可归因于子盆地共振模式随盆地宽度的增大逐渐由二维共振向一维共振变化。随着子盆地尺寸由100 m逐渐增加至400 m,子盆地区域最大PGA处提取得到的基频分别为0.83 Hz、0.7 Hz、0.6 Hz与0.54 Hz,子盆地的共振频率逐渐接近其对应的一维土层共振频率0.5 Hz。其中:工况w2a2Vs1p1基频0.7 Hz最接近于输入地震动Kobe波傅立叶谱最大峰值处频率0.732 Hz。因此,该工况地震反应也最为强烈。

2.3 子盆地相对位置对盆地地震反应的影响

含不同位置子盆地的沉积盆地PGA放大系数的分布如图9所示。从图中可以看出:随着子盆地向沉积盆地中央移动,可以看出子盆地区域的PGA放大系数逐渐增大。这是由沉积盆地垂直向一维共振与子盆地聚焦效应共同作用的结果;同时沉积盆地中央区域的PGA峰值逐渐减小并向右侧移动(移动的距离较大),这是因为越偏离盆地中心一维共振的强度越弱,而子盆地的存在导致共振强度中心向右移动,且随着子盆地的右移而向右偏移。

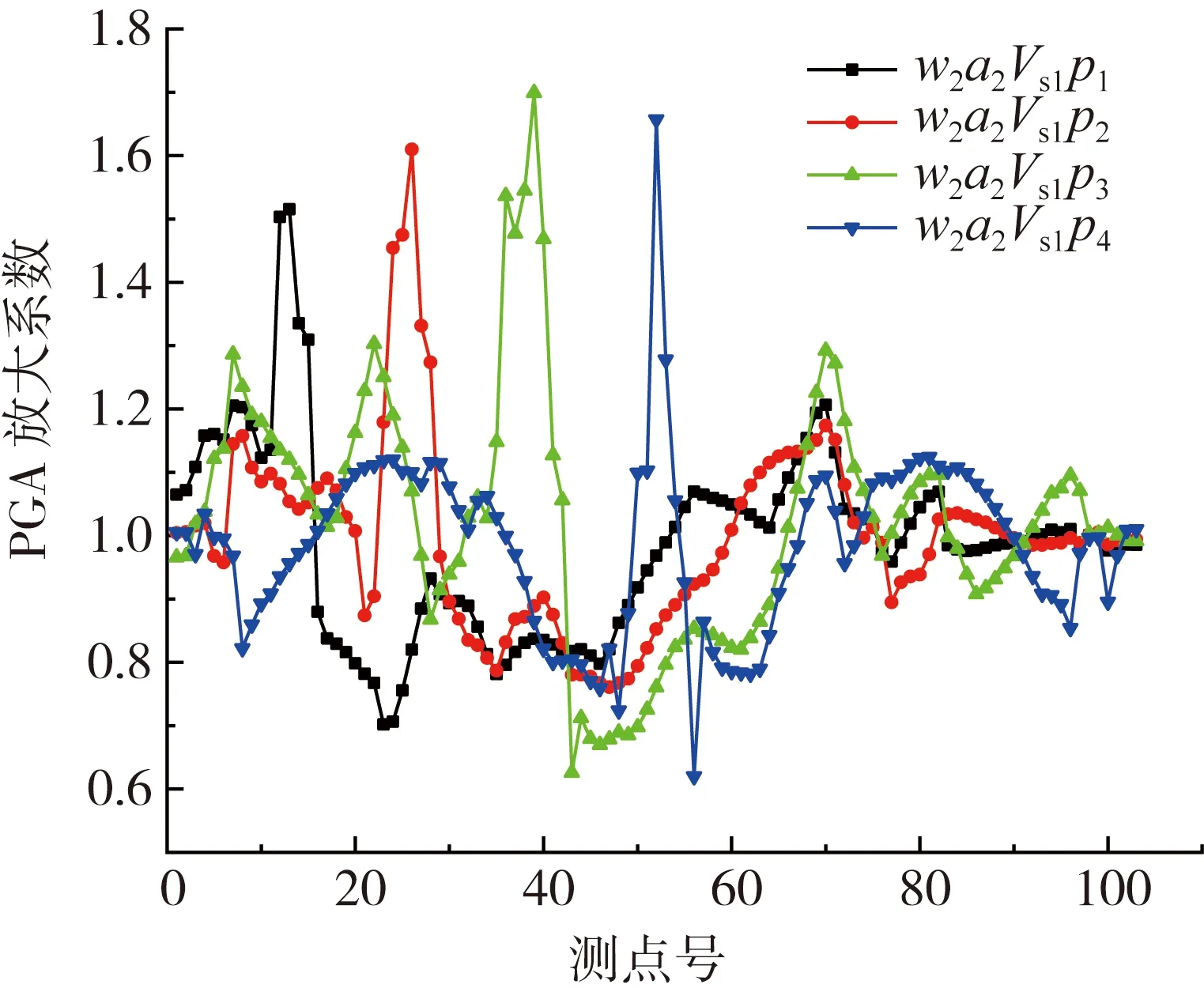
图9 工况2、5、6和7沉积盆地地表PGA放大系数分布Fig. 9 PGA amplification factor distributions of cases 2 ,5, 6, and 7

子盆地的存在对整个盆地的PGA及其放大系数的分布具有很大的影响,几乎整个盆地区域的PGA均发生了改变;同样在子盆地外右侧区域的出现PGA被抑制的现象。这里仍以子盆地区域PGA最大处的观测点代表子盆地区域(无子盆地的工况代以边缘区域),以向右偏移的盆地中央PGA峰值处的观测点代表中心区域,各个工况子盆地和中心区域的PGA及其放大系数见表4,绘制两处区域的地表PGA及放大系数随子盆地位置变化曲线如图10所示。

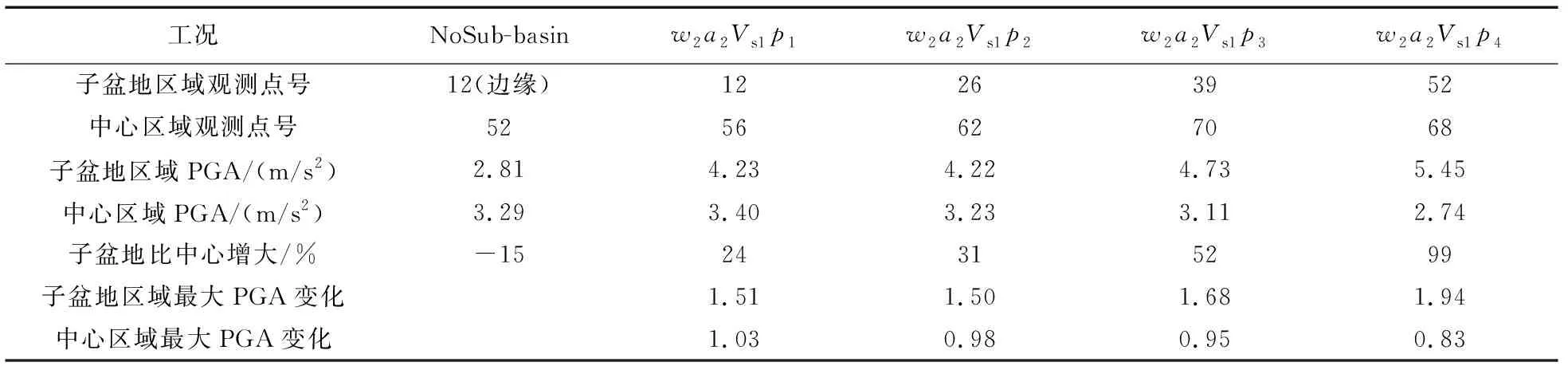
表4 工况2、5、6、7盆地中心与子盆地区域对应的观测点号、PGA及其放大系数Table 4 Observation point number, PGA and amplification factor corresponding to the centre area and the sub-basin area in cases 2 ,5, 6, and 7

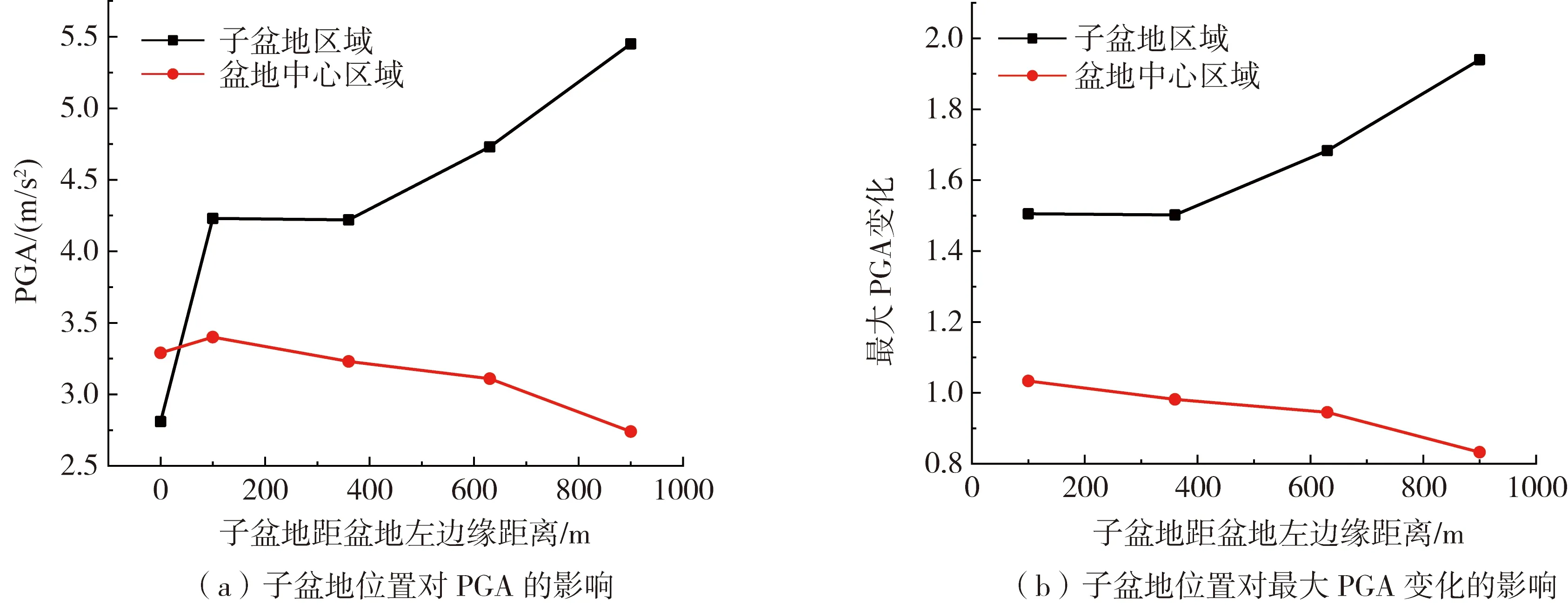
图10 子盆地位置对两处区域PGA及最大PGA变化的影响Fig. 10 Influence of the sub-basin location on the PGA maximum of basin edge and central area

从图10中可以看出随着子盆地向沉积盆地中心移动,子盆地区域的PGA及最大PGA变化逐渐增大,并在盆地中心时达到最大,且都大于NoSub-basin工况由边缘效应的PGA;盆地中心区域的PGA及其放大系数则一直减小,只有在子盆地位于盆地左侧边缘100 m时其PGA才略大于NoSub-basin工况的PGA。

子盆地区域PGA最大值(w2a2Vs1p4)比最小值(w2a2Vs1p1)大了约29%。盆地中心区域PGA最大值(w2a2Vs1p1)比最小值(w2a2Vs1p4)大了约24%;同一工况中,由于子盆地聚焦效应和沉积盆地共振效应,在子盆地中心的PGA比盆地其他区域的大,由表3-表5可知:工况w2a2Vs1p4中,子盆地区域PGA比沉积盆地中央区域增大的幅度最大,达到了99%左右。

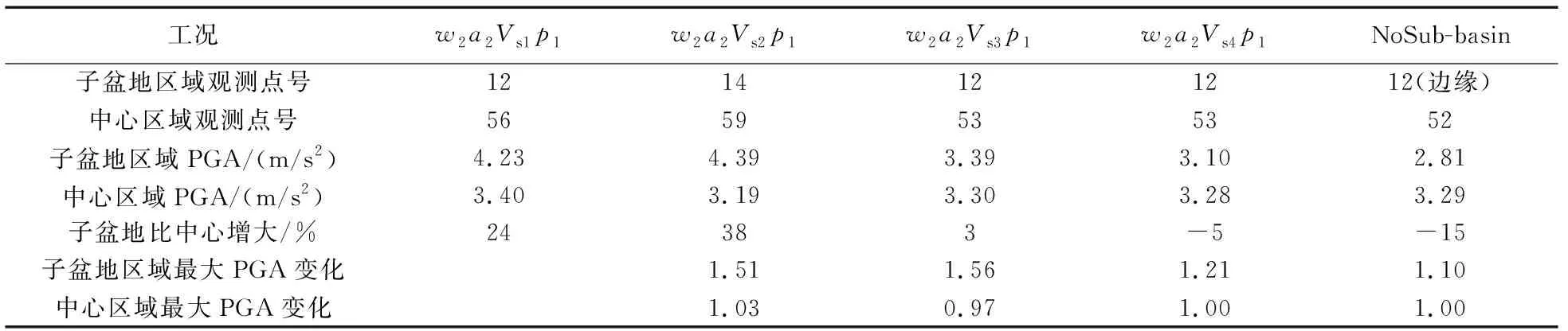
表5 工况2、8、9、10盆地中心与子盆地区域对应的观测点号、PGA及其放大系数Table 5 Observation point number, PGA and amplification factor corresponding to the centre area and the sub-basin area in cases 2 ,8, 9, and 10

2.4 子盆地介质波速对盆地地震反应的影响

不同介质波速的子盆地对沉积盆地PGA放大系数分布的影响如图11所示。从图中可以看出:随着子盆地介质波速的增大,其对盆地PGA及其放大系数产生了较为明显的影响,且存在一定的规律。

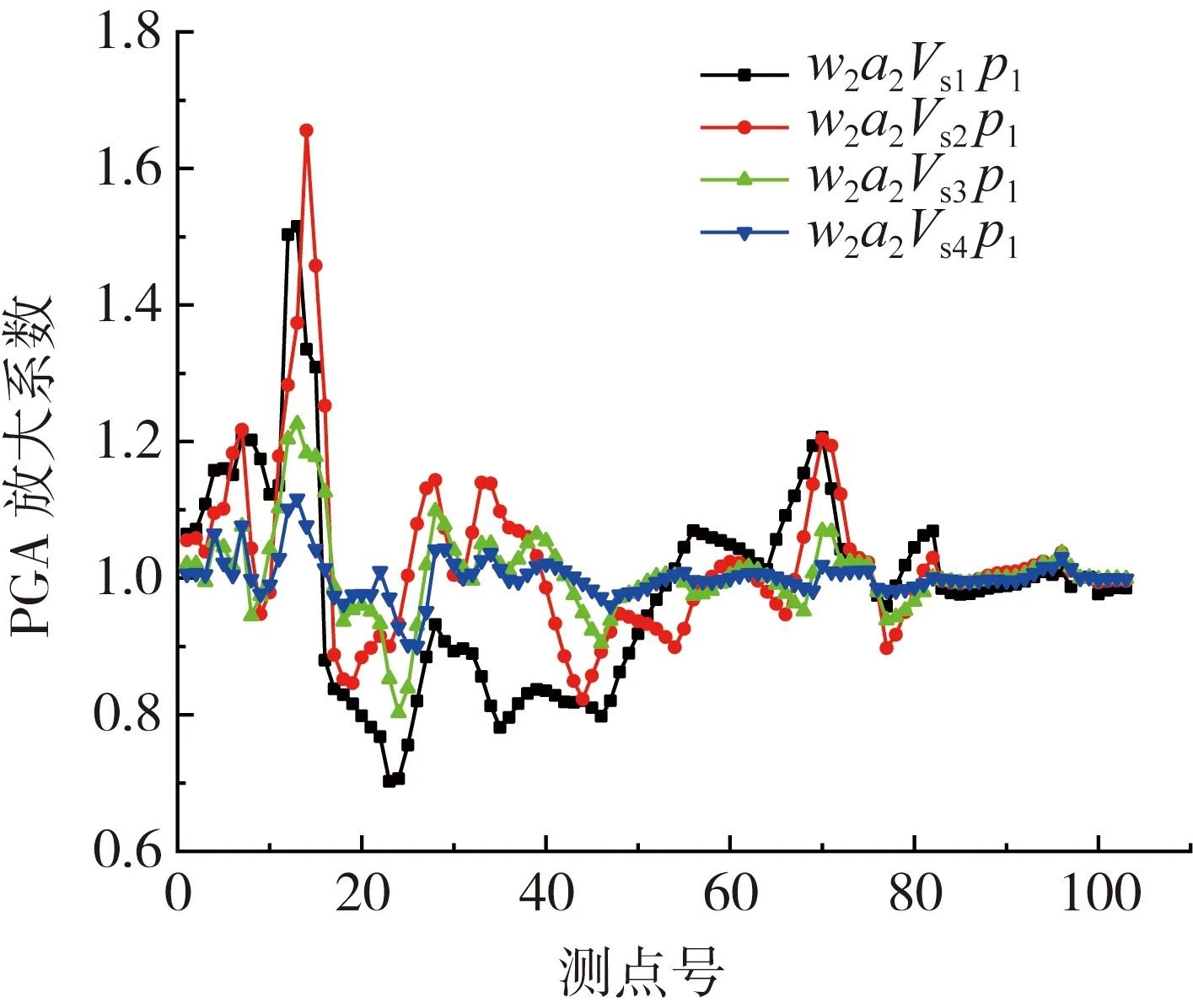
图11 工况2、8、9和10的沉积盆地地表PGA放大系数分布Fig. 11 PGA amplification factor distributions of cases 2 ,8, 9, and 10

由于子盆地的聚焦效应使得子盆地中的PGA剧烈放大,随着子盆地介质波速增大,放大程度逐渐减小,到工况10波速为250 m/s时,子盆地聚焦效应的PGA小于盆地中央处一维共振的PGA;在子盆地外右侧被抑制的PGA随着子盆地介质波速增加而增大,并逐渐接近NoSub-basin工况的幅值,沉积盆地中央区域的PGA分布也随着子盆地介质波速增加而逐渐接近NoSub-basin工况的分布,在波速为250 m/s的工况10中:其PGA分布和NoSub-basin工况的基本重合。

仍以子盆地区域最大PGA的观测点代表子盆地区域(无子盆地的工况代以边缘区域),以盆地中央PGA峰值所在的观测点代表中心区域,各个工况子盆地、中心区域的PGA及最大PGA变化见表5,绘制两处区域的地表PGA及最大PGA变化随子盆地波速变化曲线如图12所示。

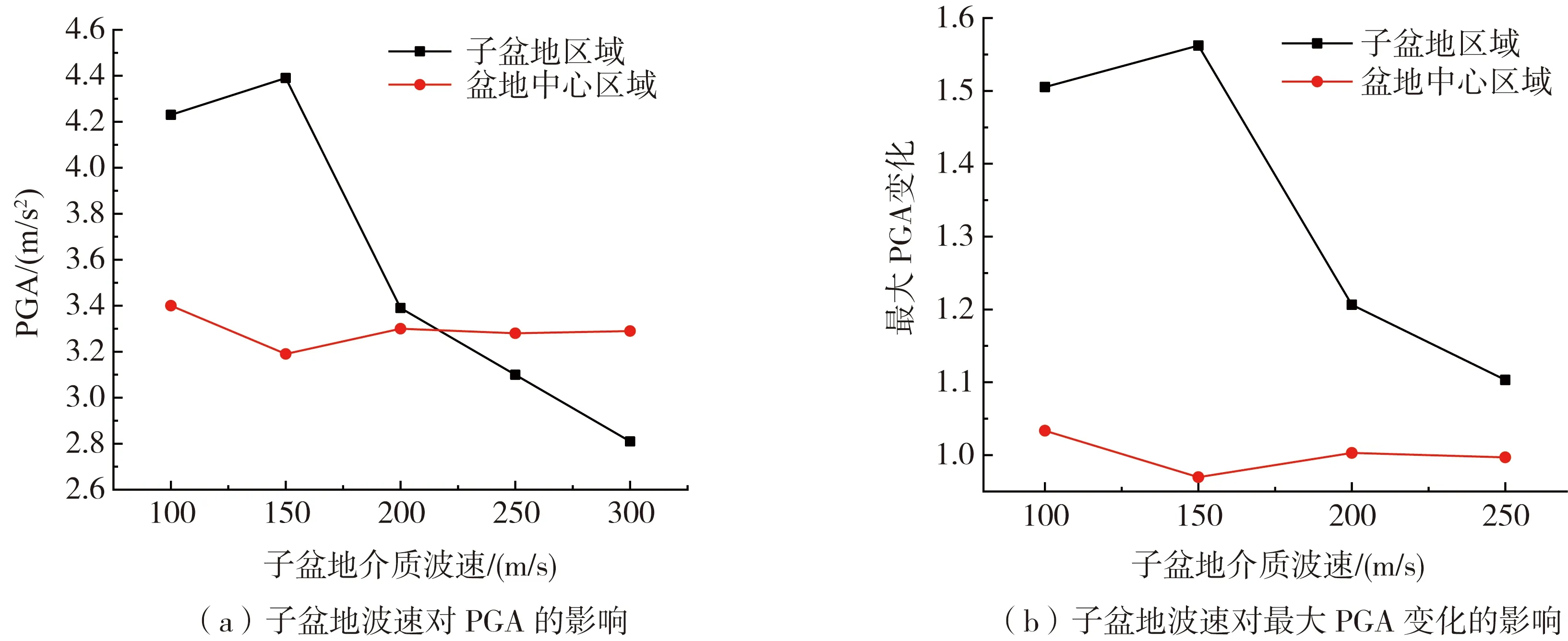
图12 子盆地介质波速对两处区域PGA及最大PGA变化的影响Fig. 12 Influence of the shear wave velocity of the sub-basin on the PGA maximum of basin edge and central area

从图12可以看出随着子盆地介质波速增加,子盆地区域的PGA及最大PGA变化先增大后迅速减小,在介质波速为150 m/s2时达到最大,此时子盆地区域的PGA为不含子盆地的1.56倍,说明子盆地聚焦效应为主的地震动放大要大于盆地边缘效应的放大;盆地中心区域的PGA及最大PGA变化则略微减小后基本保持不变,其数值与NoSub-basin工况十分接近,说明介质波速变化对盆地中央的地震反应影响有限。由于子盆地聚焦效应,在子盆地中心区域,其PGA一般比沉积盆地其他区域的大,但随着子盆地介质波速增加,子盆地区域的PGA不断下降,在工况w2a2Vs4p1中,子盆地区域PGA比沉积盆地中央区域要小5%左右。

2.5 外围盆地倾角对盆地地震反应的影响

不同倾角的沉积盆地PGA分布如图13(a)所示。从图13可以看出:由于子盆地的聚焦效应导致子盆地中的PGA剧烈增大,同一工况下其幅值几乎是整个盆地中最大的,并且随着沉积盆地倾角增大,子盆地距离盆地左侧边缘距离变短,子盆地处的观测点编号自然减小,子盆地的PGA随之减小并向左移动;在子盆地外右侧区域的PGA相比沉积盆地右侧边缘出现被抑制的现象;在沉积盆地右侧边缘区域可以看到随着沉积盆地倾角增大,由盆地边缘效应得到的PGA随之增大,这是由于面波幅值随着沉积盆地倾角增大而增大;中央区域一维共振得到的PGA要大于盆地边缘效应的,并且随着沉积盆地倾角增大,PGA分布的峰值点向右移动,PGA减小。

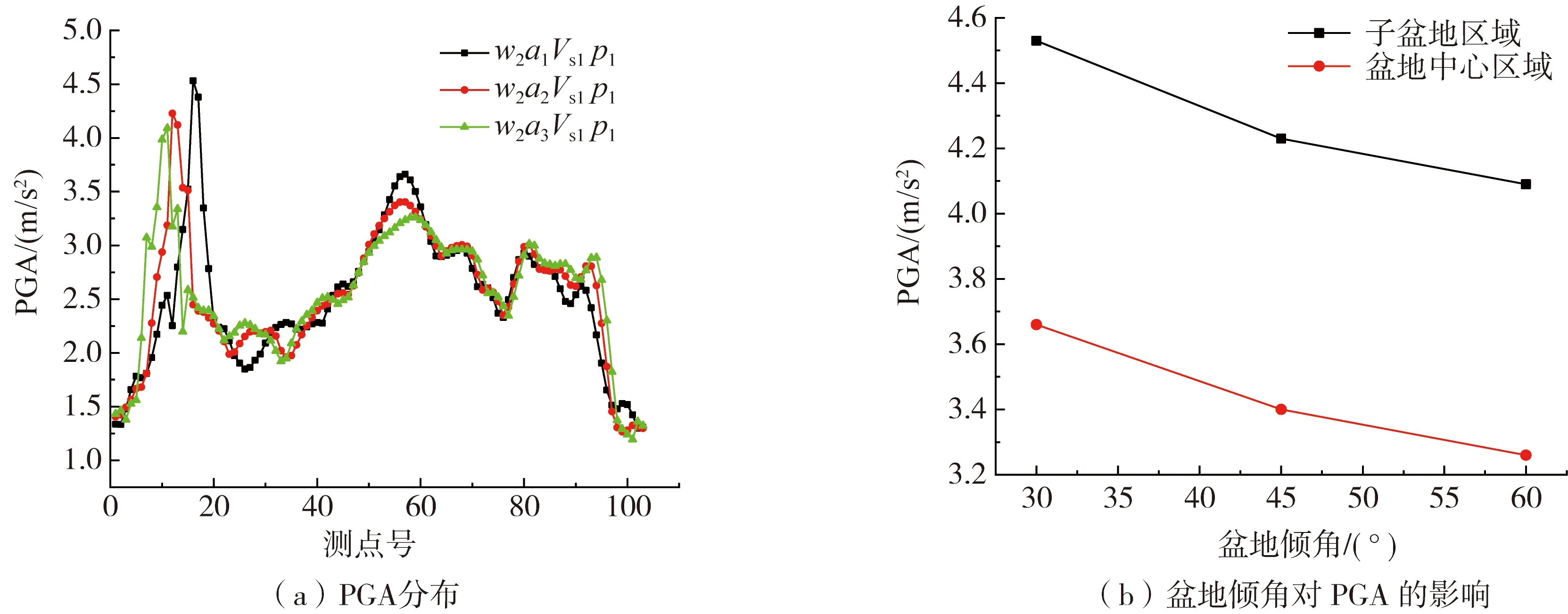
图13 沉积盆地地表PGA分布及盆地倾角对PGA的影响Fig. 13 Influence of the dip of basin edge on the PGA maximum of basin edge and central area

以子盆地区域最大PGA的观测点代表子盆地区域,以盆地中央PGA峰值点的观测点代表中心区域,各个工况子盆地和中心区域的PGA见表6,绘制两处区域的地表PGA随盆地倾角变化曲线如图13 (b)所示。

表6 工况2、11、12盆地中心与子盆地区域对应的观测点号、PGA及其放大系数Table 6 Observation point number, PGA and amplification factor corresponding to the centre area and the sub-basin area in cases 2 ,11, and 12

从图13 (b)可以看出随着沉积盆地倾角增加,子盆地区域和沉积盆地中央区域的PGA随之减小,子盆地区域PGA最大值(w2a1Vs1p1)比最小值(w2a3Vs1p1)大了约11%。盆地中心区域PGA最大值(w2a2Vs1p1)比最小值(w2a3Vs1p1)大了约12%;由表3-表6可知:三种工况中子盆地区域PGA比沉积盆地中央区域增大的幅度大致相当,在工况w2a3Vs1p1中,子盆地区域PGA比沉积盆地中央区域增大的幅度最大,达到了25%左右。

3 结论

本文以理想二维梯形沉积盆地为例,针对盆地-子盆地体系地震反应,以盆地表面PGA为评价指标,从子盆地尺寸、盆地-子盆地相对位置、子盆地介质波速和外围盆地倾角四个方面,基于数值模拟方法研究了子盆地对盆地地震反应的影响,获得以一些规律性的认识。主要结论如下:

1)子盆地具有明显的聚焦效应,使得子盆地内的地震动响应剧烈增强,PGA得到大幅放大;子盆地的存在对整个盆地的PGA及其放大系数的分布产生了很大的影响,相比不含子盆地的工况,子盆地区域PGA可能被放大约2倍左右。

2)随着子盆地尺寸增加,子盆地内波动的幅度变大,波动持续时间延长,沉积盆地中央区域PGA幅值增大并略微向右移动,中央区域PGA放大最大约1.1倍左右。此外,子盆地靠近盆地中央区域时,子盆地对PGA的影响最大,随子盆地位置由靠近盆地边缘移动至盆地中央,PGA放大系数由1.5左右增大至2左右。

3)子盆地介质波速与其周围土体波速相差越大,子盆地的影响越明显,随介质剪切波速增加,子盆地区域PGA放大系数减小至1.1倍左右,但中央区域则变化不大。此外,随外围盆地边缘倾角的增大,子盆地区域PGA幅值随之减小并向左移动,沉积盆地中央区域PGA幅值也随之减小,而盆地由边缘效应得到的PGA幅值则有所增大。