基于改进ACO算法的工程项目物流成本管理应用研究

张佑健，李 莉，吴 瑕，狄宏林

(1.东莞开放大学，广东 东莞 523000；2.惠州学院，广东 惠州 516007)

0 引 言

在电力市场中，电网企业为了能够提高其市场竞争力，企业的管理模式需要发生改变，转移到以经济效益为中心[1-3]。而其涉及的物流管理模式影响着企业的成本控制、经济效益等方面。因此，在进行电网企业成本控制时，可以对其工程项目物流成本进行降低，以此来降低企业成本，提高竞争力。然而，在当前电网企业成本管理中，相关工程造价制度并未涉及物流成本科目，使得企业对工程项目物流成本的掌控难度较大。如此一来，便对施工管理形成一定阻碍，不利于提高施工管理水平，从而影响电网企业经济效益。有些学者面对集装箱码头成本管理时，在时间驱动的基础上，提出了改进作业成本法(activity-based costing approach，ABC)，能识别货物装卸过程的瓶颈，以及计算其装卸成本，并全面分析相关物流活动及成本，结果表明了该方法的有效性[4]，因此，文章将ABC法应用在电网企业工程项目物流成本分析中。面对既有铁路的优化设计问题，蚁群算法(ant colony optimization，ACO)发挥其空间组合优化性能，进行最优交点组合寻找。结果显示，该算法的应用效果不错[5]。因此将其应用在电网企业项目管理中，对项目物流成本进行优化，以期降低工程项目物流成本。

1 基于ABC算法和改进ACO算法的电网工程项目物流成本优化研究

1.1 ABC算法在工程项目物流成本模型构建中的应用

在电网企业项目管理中，以往的物流管理模型不再适应当前的发展需求，需进行管理方式的转变。通过优化工程项目物流成本，降低经营生产成本，以此来获得更强的市场竞争力。在一个电网工程项目全寿命周期中，包含了许多的物流工序，这些工序包含的工期和成本不同，通过相关逻辑关系形成了工程项目的物流成本。想要降低物流成本，就需对每道工序的工程、成本进行优化，从而解决工期-成本问题(time-cost-trade-off-problem，TCTP)。对TCTP进行分析，首先，确定每个物流工序实施方案。并对项目工期-成本的关系进行确定，画出均衡曲线。其中物流工期目标的数学表达式见式(1)。

(1)

图1 项目物流成本

图1中，物流成本有订货成本等9种成本组成，从而得到项目物流成本C计算公式见式(2)。

(2)

式(2)中，i′为选择的方案，方案总数是m。处理工期与成本采用无量纲化处理方式，得到物流成本优化模型目标函数，相关公式见式(3)。

Z=C+T

(3)

式(3)中，Z表示目标函数。在模型中，想要解决TCTP，便需从零列到n列的线路中，获取一条线路，使成本目标和工期最小。在物流成本中，合适的核算办法可以明了物流各流程的成本花费情况，知晓物流过程的瓶颈。对此，文章采用ABC法。有别于以往的成本分析法，ABC法的潜在假设是因生产产品或提供服务出现了作业活动，在该活动中会产生费用成本。该方法能够对整个项目物流成本构成进行分析，给出的相关费用信息更精准。在该项目物流中，起始于物料供应商，通过不同物料环节的运输等操作，最终达到施工现场，并进行相关组装工作。期间，涉及的作业活动均属于物流链，这些活动消耗的资源费用汇总起来，并形成了物流成本。在ABC法中，包含了图1中的9种成本的费用情况，具体如图2所示。

图2 相关物流成本情况

从图2中，可以知道不同物流模式的物流成本，根据对应的计算公式得到相应的物流成本，为物流成本优化做准备。在物流工序中，不仅要计算物流成本，还需对工期进行计算。在电网工程项目实施过程中，由于施工工艺难度大等不定因素的影响，易增大建设工期风险。想要更高效地完成项目中的物流过程，需对期间的工期计算模型进行构建。考虑到多因素制约的情况，文章将不可变因素设置成限制条件，而优化目标是可变因素，从而进行相关合理工期的确定，最终得到正常状态下物流总工期，见式(4)。

T=min(tj-ti)，tj-ti≥ttjr，tj≥ti，ti≥0，i∈[1，n-1]

(4)

式(4)中，设置工序ij的开始时间、结束时间、正常完工时间分别为ti、tj、ttjr，也就是说tijr是工序ij的工序期望值。

1.2 改进ACO算法在工程项目物流成本优化中的应用

在构建了项目物流成本模型后，对模型进行优化。该问题属于组合优化问题，而ACO算法在该类型问题求解上具有较好的性能，因此，文章选取ACO算法，解决物流成本优化问题[6-7]。在问题解决的过程中，将其转化成旅行商问题。由于算法的信息素发挥因子会较大程度地影响算法的运行情况，使全局搜索能力及收敛速度发生较大变化，因此，可以利用修正自适应权重法进行算法优化。其中工期和成本目标的权重见式(5)。

(5)

(6)

式(6)中，f(X)表示综合目标值，将一次循环产生的解的序号设置成X，第X个解的成本目标值设置成Zc，该解的工期目标值设置成Zt，r表示随机数，均布的范围为[0，1]，为防止f(X)出现零或无效值的情况，一次循环后，对路径τ更新值进行计算。对各边的信息素挥发度进行更新，对蚂蚁选择各边的概率进行计算，见式(7)。

(7)

式(7)中，i、j1、j2分别表示当前工序、下次工序、下下次工序的实施方案序号，α、β表示参数，α、β可以分别对信息素、路径的相对重要程度进行控制，将边(i，j1，j2)可见度设置成ηi，j1，j2，代表搜索过程中的局部信息。通过ACO算法给蚁群的蚂蚁选择路径，具体见式(8)。

(8)

式(8)中，J表示确定的概率进行选择，q表示随机数，其均布的范围为[0，1]，q0是[0，1]中的参数。把搜索的新解放至解库，对E进行更新，重复分配vc、vt与更新E之间的步骤，直到满足终止条件位置。由此可得物流成本优化的流程见图3。

图3 物流成本优化流程

2 基于改进ACO算法的电网工程项目物流成本优化应用分析

对文章使用方法进行验证，数据来源于某高压输变电工程造价项目现有数据和某物资公司提供的相关数据，经过模拟后得到文章所需的项目物流成本数据，这些数据可反映项目物流成本特点。在项目物流成本中，拥有的工序为9个，这些工序包括订货、采购、仓储等内容，每个工序有5个备选方案。首先，通过收集的项目实际数据，获取每个工序物流成本与工期的关系，对物流成本进行模拟，将得到的相关数据设置为样本。通过改进ACO算法，对项目物流成本目标函数的最优解进行搜索。由于参数会对改进ACO算法最优解搜索速度造成影响，因此，选取合适的参数较为重要。设置蚂蚁参数为m，设置信息素挥发度为ρ，将信息、期望两种启发式因子分别设置为α、β，信息素总量为Q=1，设置最大迭代为80。首先，设置m=30，ρ=0.7，研究不同α、β组合下算法的性能情况，如图4所示。

图4 不同、组合下算法的性能

图4中，不同α、β组合下改进ACO算法的目标函数值不同，算法目标函数值最小的组合为组合7，该组合的算法目标函数值为0.4434*105，根据物流成本最小化的要求，组合7对应的α、β值符合要求，即算法参数α、β取值应分别以该参数为基础，研究不同蚂蚁数下改进ACO算法的目标函数变化情况，如图5所示。

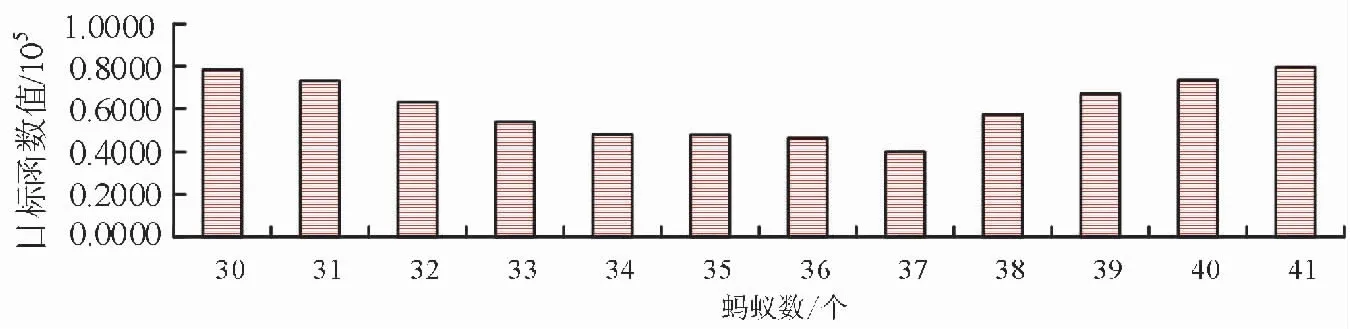
图5 不同蚂蚁数下改进ACO算法的目标函数值

图5中，随着蚂蚁数的增加，改进ACO算法的目标函数值先逐渐降低后逐渐提高。改进ACO算法目标函数最小时对应的蚂蚁数为37，此时的目标函数值为0.4008*105。根据目标函数值大小可知，蚂蚁数取值为37时，最符合要求，因此将其作为改进ACO算法最终确定的蚂蚁数。在此基础上，研究不同信息素挥发度ρ下改进ACO算法的目标函数变化情况，如图6所示。

图6 不同信息素挥发度下改进ACO算法的目标函数值

图6中，随着信息素挥发度的增大，改进ACO算法目标函数值先逐渐减小后迅速增大。从目标函数值大小可知，信息素挥发度取值为0.7时，最符合要求，此时可获得最小的物流成本。因此，将其作为最终的信息素挥发度值，从而确定了ACO算法最终的α、β、m、ρ值。参数确定后，研究该算法在不同函数下的适应度值与运行时间如图7所示。

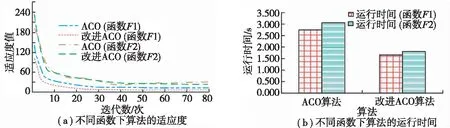
图7 不同函数下算法的性能

图7a中，函数不同，两种算法的适应度不同；同一函数下，迭代数不同，算法适应度不同。在函数中，改进ACO算法适应度曲线总位于ACO算法下方，且前者比后者先出现收敛情况。图7b中，不同函数下算法的运行时间不同。在函数F1中，改进ACO算法的运行时间为1.657 s，比ACO算法少1.089 s；在函数F2中，改进ACO算法1.809 s。由此可见，改进ACO算法性能更佳。设置最大迭代为80，ACO算法为对比算法，研究文章使用的改进ACO算法和ACO算法在电网工程项目物流成本优化中的应用结果，相关内容如图8所示。

图8 两种算法的应用结果

图8中，随着迭代次数的增加，改进ACO算法和ACO算法的工期-成本综合目标值呈下降趋势，并最终稳定下来。从算法对应的折线图可以看出，改进ACO算法对应的折线图位于ACO算法的下方，即相同迭代下改进ACO算法的工期-成本综合目标值总是小于ACO算法。当迭代次数为20时，改进ACO算法的工期-成本综合目标值为0.50817*105，比ACO算法小0.2491*105；当迭代次数为40时，改进ACO算法和ACO算法的工期-成本综合目标值分别为0.3988*105和0.6952*105。当迭代次数为45时，改进ACO算法的工期-成本综合目标值为0.3790*105，且为其收敛迭代次数；而ACO算法的收敛迭代数为72，该算法的工期-成本综合目标值为0.5319*105，ACO算法的收敛迭代数比其少27，明显比改进ACO算法大。由此可见，改进ACO算法优于ACO算法。

3 结 论

为降低电网企业工程项目物流成本，实现企业项目优化管理，文章在TCTP的基础上，构建工程项目物流成本模型，利用ABC法核算该模型，并通过进行物流工序工期的计算。在工程项目物流成本模型优化中，将TCTP转换为旅行商问题，将自适应权重和ANN算法融入到ACO算法中，对ACO算法进行改进，以此来提高算法全局收敛能力，并将该算法应用在工程项目物流成本优化中。结果显示，α、β、m、ρ值会较大影响改进ACO算法的性能。固定其他参数，在组合7中，算法目标函数值最小为0.4434*105，即算法参数α、β最佳取值均为0.2。固定其他参数，蚂蚁数为37，最小目标函数值为0.4008*105，即蚂蚁数m最佳取值为37。固定其他参数，当信息素挥发度为0.7，对应的目标函数值最小为0.3790*105，即ρ=0.7为最佳信息素挥发度。在不同函数下算法性能检测中，改进ACO算法的收敛性更好、运行时间更短，在函数F1中，改进ACO算法的运行时间为1.657 s。在参数确定后的改进ACO算法应用分析中，改进ACO算法优于ACO算法，其收敛迭代数更少，为45，工期-成本综合目标值更小，为0.3790*105。由此可见，文章采用方法应用效果较好。在今后，还可以进行更多约束条件的设置，进一步缩小项目物流成本与实际情况的差距。