大型方箱真空容器结构设计中的有限元分析与优化

胡乃涛

（辽宁轨道交通职业学院，辽宁 沈阳 110023）

由于大气环境中的氧气具有强氧化性，因此很多科学研究和生产都需要真空环境。在工业生产中，随着产量的增加，迫切需要大型真空环境。大型真空环境的设计非常复杂，需要考虑容器的强度、刚度和稳定性，并且需要设计可靠的密封结构。除此之外，在工业应用中还需要考虑空间、工艺流程、工艺环境等，因此设计大型真空环境是个庞杂的系统问题。

有研究人员在大型真空容器的设计分析进行了大量工作，韩潇[1]根据需求分析设计了圆筒形大型真空容器，并且对其不连续区域进行了应力分析，对整体进行了稳定性分析和优化设计，提高了大型真空容器的可靠性并且降低了成本，表明有限元法在大型真空容器的设计过程中是一个重要补充。孙志明等[2]对某大型圆形真空容器进行了设计，并且仔细描述了有限元分析过程，得出了总体变形量和法兰变形量，并且进行了稳定性分析，给真空设备开口法兰补强提供了依据。孟冬辉等[3]为了提高空间利用率采用了大型方箱型真空容器，采用有限元分析对真空容器的强度、刚度和大型法兰变形量进行了分析，最后进行屈曲分析，证明了容器设计满足要求。

在分析文献过程中发现，大型方箱真空容器受力情况较圆形容器差，设计过程复杂，但是方箱结构具有空间利用率大的优点。本文采用ANSYS-Workbench 软件对大型真空方箱结构的3 种方案、真空方箱门及转轴系统、支承结构进行了有限元分析，阐述了大型真空方箱结构设计优化的过程，为相关设计提供参考。

1 方箱真空容器结构设计

按照某环境系统设计要求，对方形真空容器进行了设计，见图1。真空容器为卧式方形结构，有效空间为长6 400 mm、高3 450 mm、宽2 800 mm。容器前方布置直径为150 mm 的观察窗、前方两侧布置两个门，根据设计要求，两个门的大小相等，均为2 770 mm×1 390 mm 的方形门，该门及门框的变形量需要小于3 mm，真空容器总体变形量需要小于5 mm。

图1 大型方箱真空容器结构三维模型

方箱真空容器设计参考《真空设计手册》[4]计算，由于内部气体具有腐蚀性，所以材料选取SUS304不锈钢，容器支承采用桁架设计，材质采用Q235A结构钢。

2 有限元分析

有限元分析是一种数值计算分析方法，首先分析前需要对实际问题进行合理简化，分析箱体的强度和刚度时，对于底部支承仅保留了四角处的支承，模型整体左右对称，因此采用的对称分析，减少参与计算的实体，有效利用计算机资源分析问题。采用Workbench 默认的实体单元，方箱箱体材料属性按SUS304 的材料属性设置，其中弹性模量取1.99×105MPa，泊松比取0.3，屈服极限取205 MPa，强度极限取520 MPa，许用应力取137 MPa，密度取7 930 kg/m3。方箱支撑腿材料属性按Q235A 的材料属性设置，其中弹性模量取2×105MPa，泊松比取0.3，屈服极限取235 MPa，强度极限取375 MPa，许用应力取138 MPa，密度取7 850 kg/m3。模型及划分网格后的图形如图2 所示。

图2 箱体简化模型及网格划分

2.1 载荷和约束

2.1.1 约束条件

方箱容器有4 个支承，由于方箱在实际工作中，4 个支承均通过螺栓固定到地基上，因此在有限元分析中，对4 个支承的底面均采用全约束。

2.1.2 载荷条件

考虑方箱结构自重对结构强度的影响，取重力加速度g=9.8 m/s2，方向竖直向下；方箱上、下、左、右、前、后6 个面在大气压强的作用下承受均布面载荷，压强为大气压强，为101.325 kPa。加载后的模型如图3 所示。

图3 约束及加载情况

3 结果与分析

3.1 方箱优化过程

模型一是没有优化的原始模型，模型二是优化过程的中间模型，模型三是最终优化的模型。对比模型一和模型二，模型二上部增加8 根加强梁，用来减小上板的变形、减小2 根长梁的变形所导致的应力集中效应，同时4 个侧面和底面也一样采用增加加强梁的方式减小变形和应力集中。对比模型二和模型三，模型三比模型二底部增加了翼板、门处增加加强筋，用来进一步减少底部变形和两个门处的变形所导致的应力集中效应，最终计算结果如图4～6 及表1 所示。

表1 箱体最大VON-Mises 应力和最大变形量

图4 模型一内部框架图

图5 模型二内部框架图

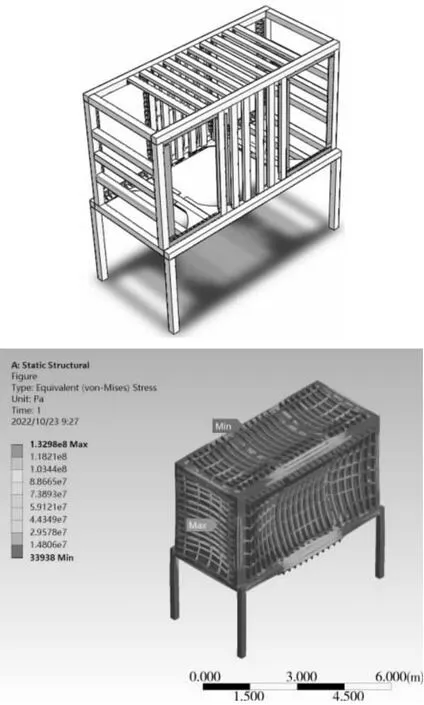
图6 模型三及VON-Mises 应力分析结果

模型三强度符合要求，并且变形量小，按照此结构设计上腔体。

3.2 门计算结果

将门及转轴系统单独进行有限元分析，将转动装置的加强筋增大为加强翼板，减少因为重力而导致的门在竖直方向的变形及综合变形，同时减小最大应力。经过计算分析，优化后门及转轴最大VON-Mises 应力为85.443 0 MPa，最大变形量为2.380 3 mm，最大竖直方向变形为1.251 5 mm。

在门设计过程中，由于有密封要求，因此在门开关过程中需要避免将密封圈损坏，并且需要和门框保留一定的间隙。综合考虑受力变形和加工制造，门框和门在上下左右方向各留出4 mm 的设计间隙，要求门由于静态变形导致的竖直方向的变形量小于2.5 mm，因此上述计算结果满足设计要求。

3.3 支腿计算结果

分析支腿过程中，将上箱体模型简化掉，并且将箱体质量38 t 均匀施加到上表面来计算支腿的应力及变形。经过计算分析，箱体支承最大VON-Mises 应力为123.180 0 MPa、最大变形为1.828 3 mm，最大应力和变形量均在许用范围内，因此强度符合设计要求。

4 结 论

（1）在优化设计大型方箱真空容器过程中，通过加强结构强度最终获得既满足强度要求又满足设计要求的方箱结构，最终结构在工作状态下的最大VON-Mises 应力为132.98 MPa，最大变形量为2.340 9 mm，满足设计要求。

（2）由于门的尺寸较大，质量也比较大，因此结构刚度需要足够才可以满足自由开关门的要求，通过给转轴添加加强筋的方式提高转轴系统结构刚度，进而降低静态变形量，通过优化后的静变形量为最大综合变形为2.380 3 mm，最大竖直方向变形为1.251 5 mm，满足使用要求。

（3）该大型方箱结构复杂，总质量达到38 t，因此支承也需要满足强度要求，经过计算，最大VON-Mises 应力为123.18 MPa，小于Q235 材料的许用应力，满足强度要求。

本文通过有限元方法对大型方箱结构进行了优化设计，计算了箱体、门和支承的最大应力以及最大变形，得到了满足强度和设计要求的模型，提高了设计效率，降低了设计成本。希望通过大型方箱真空容器结构设计的有限元分析与优化设计，为其他真空设备的设计起到借鉴作用。