一种经济型磁通耦合式直流限流器
2023-10-31李国城李光茂陈磊乔胜亚郑服利朱璐张旭阳
李国城,李光茂,陈磊,乔胜亚,郑服利,朱璐,张旭阳
(1. 广东电网有限责任公司广州供电局, 广州 510410;2. 武汉大学电气与自动化学院, 武汉 430072;3. 国家电网河南省电力公司, 郑州 450000)
0 引言
“双碳”背景下电力系统朝着电力电子化方向演变,直流输电技术迎来新一轮快速发展机遇[1-3]。传统基于晶闸管的直流输电技术由于其存在换相失败风险、无法进行无功控制等缺点,已逐渐被基于全控型器件的柔性直流输电技术取代[4-7]。然而,综合考虑成本及换流性能,柔性直流输电系统的换流器常采用半桥型MMC,其不具备直流故障自清除能力[8-10]。换而言之,半桥型模块化多电平转换器(modular multilevel converter, MMC)一旦遭遇直流故障,短路电流在数毫秒内将达十几倍甚至数十倍的额定电流,给直流断路器开断带来重大挑战[11-13]。为了降低直流断路器的分断应力,有效、经济的直流故障限流方法是柔性直流输电建设发展的关键技术[14-16]。
目前,直流故障限流方法技术路线包括平波电抗器、电阻型限流器和电感型限流器。其中,平波电抗器其限流原理简单、限流效果好,但严重影响直流系统动态响应特性及系统稳定性[17-18];电阻型限流器基于高温超导材料的失超机理进行故障限流,具有响应快、自恢复等优点,但成本高、恢复速度慢[19-21];而电感型限流器的工作原理各异,其优势在于成本低。文献[22]提出了一种利用晶闸管换流和换相电容触发关断的固态式电感型直流限流器,采用成本低廉的晶闸管进行两次换流,巧妙利用两条换流支路对电容的充放电来关断晶闸管。文献[23-24]参考了混合式直流断路器(direct current curtain breaker, DCCB)的换流设计理念,提出了一种固态式电感型直流限流器,采用三对反向并联晶闸管阀组和一对预充电电容,经三次换流过程将限流电感投入主回路。文献[25]借鉴类似换流原理,利用阻容型元件的平滑特性和负荷转移开关的快速响应特性,提出了一种固态式限流器。上述固态式直流限流器涉及开关器件开断和电流换流,其动作机制复杂、可靠性较低。另外,正常工况下负荷转移开关流过额定电流,通流开关损耗高。文献[26-27]提出由一对耦合线圈反向并联构成的耦合式电感型限流器,但仍需要负荷转移开关来进行换流。文献[27]将耦合电感的异名端连接起来,构成故障隔离限流器,但仍需3 个开关群来控制故障电流流通路径。上述文献所述的电感型限流器在动作时需均依赖于负荷转移开关将主回路电流先换流至限流支路,才能进一步限流。负荷转移开关需具备一定的电流开断能力,而其由大量的电力电子开关器件构成,因此固态式限流器成本仍较为高昂,影响其在直流电网中大规模推广应用。此外,负荷转移开关在正常工况下也会流通电流,带来较大通态损耗。
本文提出了一种经济型磁通耦合式直流限流器,大量减少了电力电子开关器件的用量。本文介绍了其拓扑结构、工作原理,推导了其数学模型,设计了限流器与直流断路器的联合运行方案,并推导了各阶段内限流器各支路的数学表达式,最后在MATLAB/Simulink 仿真平台验证了理论的正确性并给出了限流器参数设计建议。
1 磁通耦合式限流器工作原理及数学模型
1.1 拓扑结构
所提磁通耦合式直流限流器拓扑结构如图1 所示,包括耦合电抗器、故障电流转移开关(fault current commute switch,FCCS)、避雷器(metal oxide arrester,MOA)。耦合电抗器由线圈1 和线圈2 组成,线圈1串联接入主电路,线圈2通过FCCS形成短路回路。避雷器并联于FCCS 两端,以限制开关动作时产生的暂态电压。
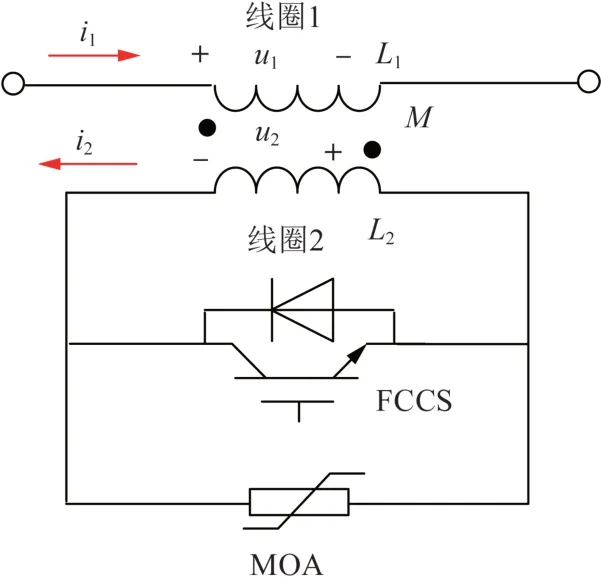
图1 磁通耦合式直流限流器拓扑结构图Fig. 1 Topology diagram of flux-coupling DC FCL
1.2 工作原理
本文所提磁通耦合式直流限流器的工作路径如图2所示,具体描述如下。
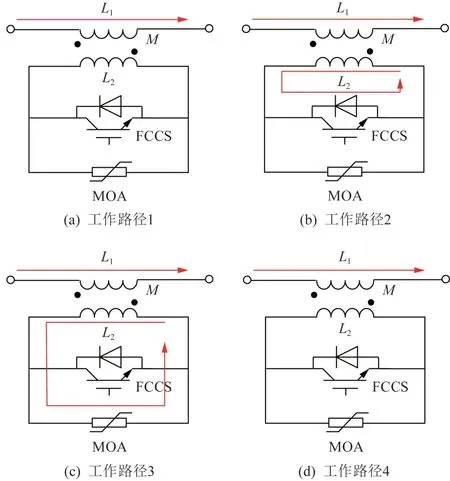
图2 所提磁通耦合式直流限流器的工作路径Fig. 2 Working path of the proposed flux-coupling DC FCL
1) 工作路径1:当柔性直流输电系统处于正常工况时,FCCS闭合,直流电流流过线圈1,工作路径如图2(a)所示。此时限流器阻抗接近于0,对系统的动态响应以及稳定性不会产生影响。
2) 工作路径2:当柔性直流输电系统发生短路故障时,FCCS 被触发前,耦合电抗器之间维持着耦合关系,限流器阻抗仍接近于0,电流流过线圈1,在线圈2 经过FCCS 形成回路,工作路径如图2(b)所示。
3) 工作路径3:FCCS 开关被触发开断后,耦合电抗器之间的耦合关系被打破,限流器呈现大电感,电流流过线圈1,在线圈2 经避雷器进行放电,工作路径如图2(c)所示。
4) 线圈2 上能量释放完毕后,线圈2 上不再流过电流,工作路径如图2(d)所示。
该磁通耦合式直流限流器的优势在于以下几点。
1) 限流原理简单,可靠性高。不涉及复杂的换流过程,仅依赖于耦合电抗器的线圈之间耦合物理关系实现限流。
2) 电力电子器件少,成本低。开关群IGBT 并联支路数和单支路IGBT 串联数均少于固态式直流限流器。
3) 正常工况下FCCS 无通流,效率高。正常运行下,FCCS 流过电流为0,不会带来额外的开关损耗。
1.3 数学模型
1.3.1 工作路径1
在此工作路径下,线圈1流过正常工况电流i1=I10,而线圈2流过i2=0。
1.3.2 工作路径2
根据图1、基尔霍夫第二定律和电容特性方程可列出方程组:
式中:i1、i2分别为主回路电流和辅助回路电流;u1、u2分别为线圈1 和线圈2 上压降;L1、L2分别为线圈1 和线圈2 自感;M为线圈1 和线圈2 之间的互感。
消去di2/dt,求解得到:
从式(2)可知,串入主回路的等效电感为L1-M2/L2。
当耦合系数k=1时,串入主回路的电感为0。
由式(1)还可得到:
t=t0时刻发生直流故障,在区间[t0,t]内对式(4)两侧积分,可得:
解得:
式中I10为故障发生时(t=t0)i1的瞬时值。
该阶段可将耦合电抗器L2解耦后等效为一个可控电流源。i2的变化趋势与i1相同,两者之间呈现线性关系。由于i2的初值为0,所以其在FCCS 动作时(t=t1)数值较小,只需要很少的IGBT 即可完成开断,有效降低了全控型器件的成本,大幅提高了限流器的技术经济性。
1.3.3 工作路径3
限流器的避雷器额定电压为UMOA1,该路径下FCCS 的端电压限制为UMOA1,可将避雷器视为一个恒定电压源,则有:
解得:
相当于将限流器等效为额定电压与UMOA1等比例缩小倍的避雷器。
由式(7)还可得:
在区间[t0,t]对式(9)两侧积分,可得:
解得:
式中I11、I21分别为FCCS 动作时(t=t1)i1、i2的瞬时值。
可见i2由三部分组成:i1相关项、时间t相关项、常数项。通常所以可忽略i1相关项,式(11)改写为:
可见电流i2近似为随时间线性下降的直线。
1.3.4 工作路径4
根据图1 和基尔霍夫第二定律可列出方程组如式(13)所示。
解得:
此时,串入主回路的限流电感为L1。
由于FCCS 已开断,且线圈2 上能量已释放完毕,电流i2=0。
2 限流器与直流断路器联合运行方案
2.1 直流断路器原理
本文选用ABB 公司所提混合式直流断路器。图3为该型直流断路器的示意结构。
正常运行时,主断路器(main circuit breaker,MCB)处于断开状态,负荷电流流经快速机械开关(rapid disconnector switch,RDS)和电流转移开关(load commutation switch,LCS)所构成支路。故障发生后,依次触发LCS、RDS 及MCB 进行换流操作,最后电流转移至避雷器支路以吸收直流回路中储存的能量,直到电流过零后断开隔离开关,最终完成直流故障清除。
2.2 联合运行步骤
图4 为磁通耦合式限流器与混合式直流断路器的联合运行步骤示意图,具体阐述如下。

图4 限流器与直流断路器联合运行示意图Fig. 4 Schematic diagram of joint operation between FCL and DCCB
1)t=t0,发生直流线路短路故障;
2)t=t1,限流器FCCS开断;
3)t=t2,线圈2上能量释放完毕;
4)t=t3,LCS 断开,MCB 闭合,迫使电流由LCS转移至MCB,待LCS电流过零,RDS断开;
5)t=t4,MCB 二次断开,随后电流转移至避雷器,吸收直流系统所储存能量;
6)t=t5,隔离开关工作开断,完成直流故障清除。
2.3 联合运行方案解析
MMC 的直流故障过程可大致划分为直流电容放电、续流二极管自然换向导通和二极管同时导通三个阶段。故障初期,直流故障电流以直流电容放电电流为主,可等效为RLC等效电路,等效电路图如图5所示。
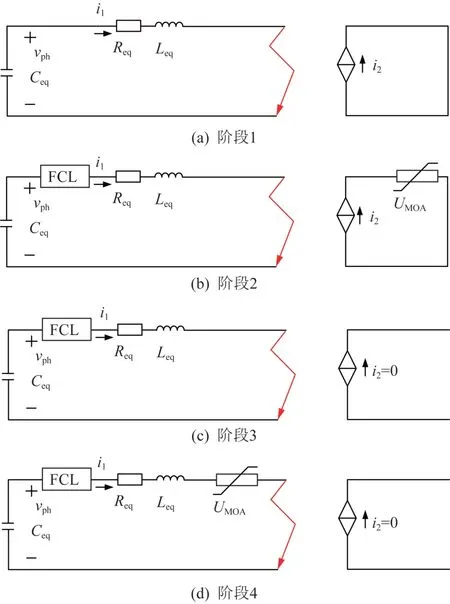
图5 限流器与直流断路器联合运行等效电路图Fig. 5 Equivalent circuit diagram of joint operation between FCL and DCCB
2.3.1 阶段1 (t0<t≤t1)
根据KVL 定律和电容器特性,依据图5(a)可列写方程组:
式中:Leq、Ceq、Req分别为MMC 故障回路等效电感、电容、电阻;vph为Ceq的端电压。
回路阻尼较小,电容放电为典型的振荡放电过程,解得:
式中:I0、V0为正常工况下i1、vph的额定值;τ0、ω0分别为阶段1-2 的衰减常数、角频率;τ0和ω0的表达式为:
根据式(6)可计算出辅助回路电流i2。
2.3.2 阶段2 (t1<t≤t2)
如前所述,相当于将限流器等效为额定电压等比例缩小k L1/L2倍的避雷器。
根据图5(b)列出方程组如式(18)所示。
解得:
式中I1、V1分别为t=t1时i1、vph的瞬时值。
根据式(12)可计算出辅助回路电流i2。
2.3.3 阶段3 (t2<t≤t4)
对于主回路,相当于串联接入电感量为L1的限流电感,根据图5(c)列出KCL 方程和电容特性方程:
式中LFCL为限流电感。
串入一个电感以后,放电过程仍为振荡放电,解方程组得:
式中:I2、V2分别为t=t2时i1、vph瞬时值;τ1、ω1分别为阶段3的衰减常数、角频率。τ1和ω1的表达式为:
该阶段辅助回路电流i2为0。
2.3.4 阶段4 (t4<t≤t5)
直流断路器中避雷器额定电压为UMOA2,在实际工程应用中,其设计遵循式(23)的原则,即:
式中Vdc为直流额定电压。
避雷器将直流断路器的端电压在UMOA2,根据图5(d)所示等效电路,可推导出主回路电流i1表达式为:
式中Ipeak、Vpeak分别为t=t4时i1、vph的瞬时值,即直流峰值电流、电压。
3 限流器综合性能评价方法
从电气应力、热应力和时间3 个维度出发,构建限流器综合性能评价体系,如图6 所示。其中,电气应力指标包括:直流电流峰值、桥臂平均电流峰值;热应力指标包括:桥臂电流产热系数以及直流断路器耗散能量;时间指标包括故障清除时间。

图6 所提限流器综合性能评价体系Fig. 6 The proposed comprehensive performance evaluation system of FCL
各指标具体计算方法描述如下。
3.1 直流电流峰值
直流电流峰值与直流断路器开断容量直接相关。峰值越小,直流断路器开断容量越低,直流断路器内电力电子器件也越少,投资成本也越低。直流电流峰值Ipeak计算方法如下。
3.2 桥臂平均电流峰值
将MMC 的6 个桥臂电流峰值包络线定义为桥臂平均电流iarm-ave,在一定程度上该指标能体现6 个桥臂瞬时电流的电气特征,将桥臂电流峰值指标从6个缩减至1个,其表达式如下。
式中:iarm-ac和iarm-dc分别为桥臂电流的交流分量和直流分量;isd和isq分别为网侧电流的d轴和q轴分量。
桥臂平均电流峰值iarm-ave-peak表示为:
3.3 桥臂电流产热系数
IGBT 不可逆损坏根本原因为热量聚集[28],引起IGBT热量聚集的阶段主要集中于故障发展初期。为了量化IGBT 热累积效应,引入桥臂电流产热系数。t=t0到t=th内,桥臂电流产热系数Gh计算如下。
式中:iarm为桥臂电流;th为桥臂平均电流过零时刻。
3.4 直流断路器耗散能量
直流断路器上的耗散能量影响到其避雷器的选型和设计,直流断路器耗散能量越大,对避雷器的要求越高。直流断路器耗散能量取决于故障清除时间和直流断路器避雷器电流,计算如下。
式中uDCCB为直流断路器端电压。
3.5 故障清除时间
故障清除时间tisolation指的是从故障发生到直流电流过零所需时间,即图4 中t=t0到t=t5这段时间,表示如下。
4 仿真验证与分析
为了验证所提限流器的数学模型及限流器和直流断路器联合运行方案解析理论分析的正确性,本节基于MATLAB/ Simulink 仿真平台,在单个换流器系统中进行仿真验证与分析,其中故障时间为t=0.5 s,在t=0.501 s 成功检测故障,限流器投入,在t=0.505 s 直流断路器的MCB 达到额定开距。MMC换流器系统主要参数如表1所示。

表1 MMC换流器系统主要参数Tab. 1 Main parameters of MMC system
4.1 限流电感对系统的影响
设置耦合系数k=0.99,电感比a=L1/L2=1。图7—11所示分别为不同限流电感下的主回路电流、限流器L2回路电流、桥臂平均电流、直流断路器耗散能量、桥臂电流产热系数。从图7 可看出,限流器能有效限制主回路电流,且当限流电感LFCL从20 mH 增加至80 mH,电流最大值从13.00 kA 降低至11.37 kA、10.30 kA、9.44 kA、8.73 kA,限流率最高可达32.86%。另外,随着限流电感增大,故障清除时间从10.90 ms延长至10.95 ms、11.05 ms、11.20 ms、11.35 ms。

图7 不同限流电感下的主回路电流Fig. 7 Main loop current with different current limiting inductance
由图8 可见,在阶段1 (t0<t≤t1),限流器线圈2回路电流i2呈现出与i1相同的上升趋势,且与限流电感基本无关,这与式(6)的推导结果相吻合。由于电感比a=1,随着限流电感LFCL=L1增大,L2随之增大,根据式(12),其斜率绝对值UMOA1/L2将减小。图中,在阶段2 (t1<t≤t2),i2近似为随时间线性下降的直线,这与式(12)的推导结果相吻合。
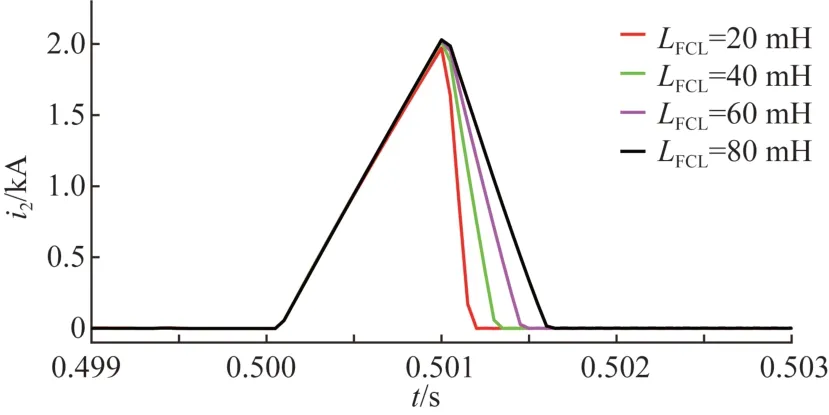
图8 不同限流电感下的限流器线圈2回路电流Fig. 8 Coil 2 loop current of FCL with different current limiting inductance
如上所述,1)主回路电流峰值随着限流电感的增大而降低;2)而在短时间内子模块电容电压基本可视为恒定电压源,所以网侧电压不变,故网侧电流也不变。综合上述两点,并结合式(26)可知,桥臂平均电流峰值随着限流电感增大而降低。图9 展现出与理论推导结果相对应的仿真结果。限流电感从20 mH增大到80 mH,桥臂平均电流峰值从4.80 kA降至4.22 kA、3.87 kA、3.60 kA、3.35 kA,限流率高达12.18%~30.22%。
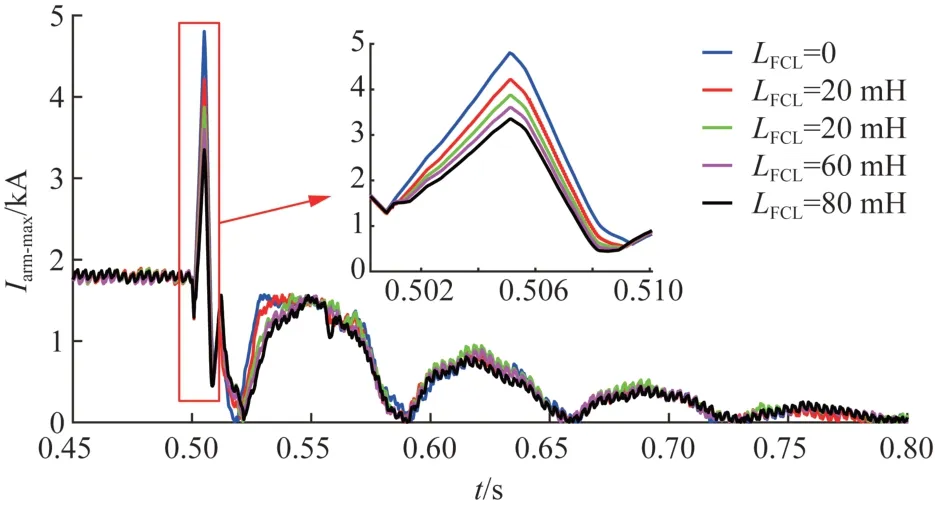
图9 不同限流电感下的桥臂平均电流Fig. 9 Bridge arm average current under different current limiting inductance
如图7 所示,限流器延长了故障清除时间,可能导致直流断路器耗散能量增大,加重直流断路器开断压力。事实上,由于限流器能有效降低主回路电流峰值,限流器能降低直流断路器耗散能量,缓解直流断路器开断热应力。且随着限流电感增大,相比未安装限流器,热应力降低了22.41%、33.62%、42.61%、50.24%,如图10所示。

图10 不同限流电感下的直流断路器耗散能量Fig. 10 Energy dissipation of DCCB with different current limiting inductance
引入限流器后,1)网侧电流不变,2)主回路电流降低。综合上述两点,结合式(28),桥臂电流产热系数将有所降低。且限流电感越大,主回路电流越低,桥臂电流产热系数越低。图11 所示的仿真结果与理论推导相吻合,随着限流电感增大,相比未安装限流器,桥臂电流产热系数降低了32.42%、48.71%、59.98%、68.27%。综上,限流器有效降低了换流器自身热应力。
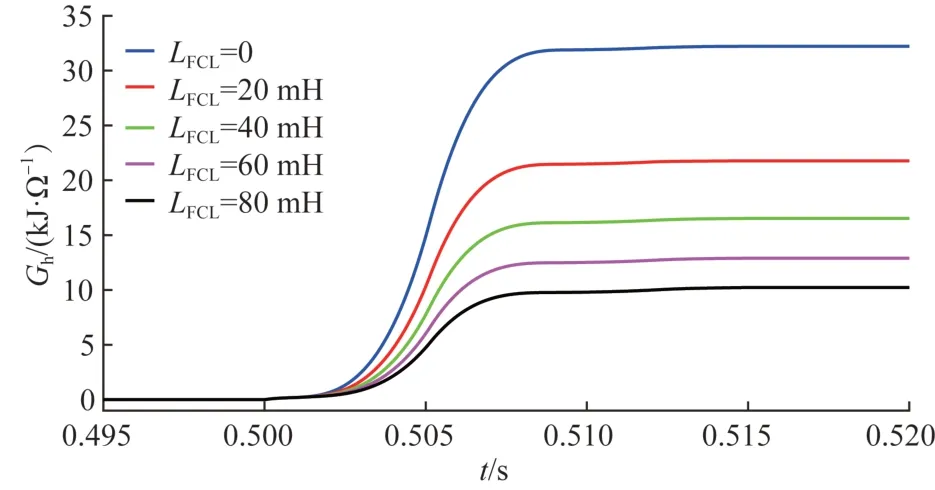
图11 不同限流电感下的桥臂电流产热系数Fig. 11 Heat generation coefficient of bridge arm current with different current limiting inductance
4.2 电感比对系统的影响
设定限流电感LFCL=60 mH,耦合系数k=0.99,电感比a=L1/L2=1~5。随着电感比增大,主回路电流、桥臂平均电流、直流断路器耗散能量、桥臂电流产热系数变化微乎其微,在此受限于版面,不给出其仿真波形。图12 所示为不同限流电感下限流器线圈2 回路电流。假设i1上升速率为k1,其为定值,由于耦合系数k不变,随着电感比a的增大,根据式(6),i2上升速率()将随之增大;根据式(12),由于L2减小,导致其下降速率(UMOA1/L2)随之增大。从图12 可看出,随着电感比增大,在阶段1 (t0<t≤t1),电流上升速率增大,且电流峰值增大;在阶段2 (t1<t≤t2),电流下降速率增大,仿真结果与理论相符。据此,推荐采用较低电感比,以降低FCCS 开断要求。具体电感比取值需兼顾FCCS及耦合电抗器成本。
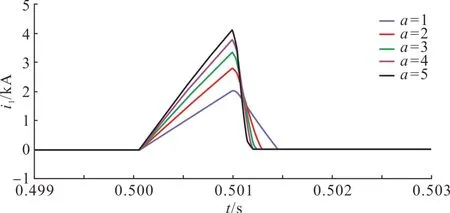
图12 不同电感比下的限流器线圈2回路电流Fig. 12 Coil 2 loop current of FCL with different inductance ratio
4.3 耦合系数对系统的影响
设定限流电感LFCL=60 mH,电感比a=L1/L2=1,耦合系数k=0.99~0.83。同样地,除L2回路电流以外其他参量随耦合系数的改变其变化微乎其微,在此不给出其仿真波形。图13 所示为不同耦合系数下限流器线圈2 回路电流。假设a不变,且i1上升速率k1不变,则随着耦合系数k减小,根据式(6),i2上升速率()将随之减小;根据式(12),由于L2不变,所以其下降速率(UMOA1/L2)不变。从图13 可看出,仿真结果与理论相对应。可见,减小耦合系数一定程度上可缓解FCCS 开断压力,但是以牺牲整个系统稳定性和快速动态响应能力为代价。基于此,推荐采用高耦合系数,并通过降低电感比来缓解FCCS开断压力。
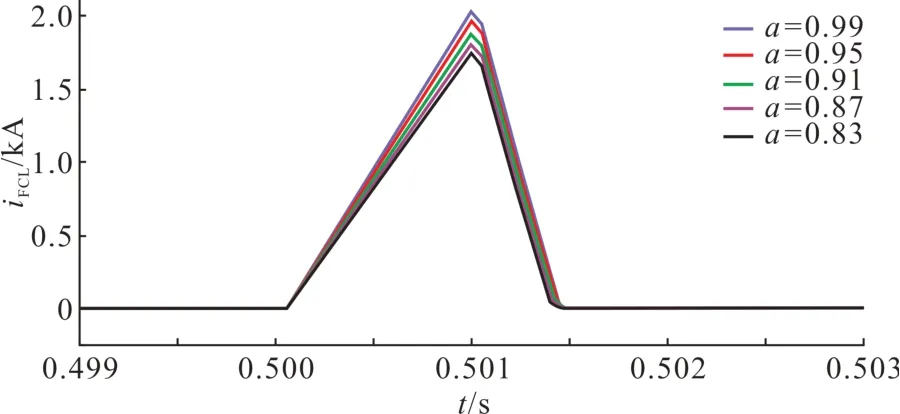
图13 不同耦合系数下的限流器线圈2回路电流Fig. 13 Coil 2 loop current of FCL with different coupling coefficient
4.4 技术经济性分析
因为投资成本主要取决于IGBT 器件的数量,可忽略其他器件的投资成本。制定方案1:文献[22]所述固态式直流限流器;方案2:所提经济型传统耦合式直流限流器。选取相对成熟的4.5 kV/1.3 kA 的5SNA 1300 K450300 IGBT 器件。对于文献[22]所述限流器,根据图7 可知,负荷转移开关开断电流为3.71 kA,避雷器额定电压为系统额定电压1.5 倍。对于本文所提限流器,FCCS 开断电流为2.03 kA,避雷器额定电压为300 kV。考虑10%的电压安全裕度和20%的电流安全裕度,两个方案的对比结果如表2所示。

表2 经济性对比Tab. 2 Economic performance comparison
由表2 分析可知,与固态式限流器相比,所提磁通耦合式限流器所使用IGBT 的数量从472 个减少到148 个,投资成本减少了68.6%,可见本文所提限流器具备更佳的经济性。
5 结论
本文提出了一种经济型磁通耦合式直流限流器,剖析了其工作原理及数学模型,解析了限流器支路电流的数学表达式。然后,给出了其与断路器联合运行步骤,并分四个阶段解析了直流电流的数学表达式。最后,根据所提限流器综合性能评价方法,在MATLAB/ Simulink 仿真平台中验证了所提限流器的数学模型及限流器和直流断路器联合运行方案解析理论分析的正确性。通过改变限流电感、电感比、耦合系数等限流器参数,得到如下结论。
1) 所提限流器综合性能佳,能有效限制直流电流峰值、桥臂平均电流峰值、桥臂电流产热系数、直流断路器耗散能量,且限流电感越大限制效果越好。但限流器将延长故障清除时间,加重了直流断路器开断压力。
2) 结合理论推导和仿真分析结果发现:减小电感比可降低限流器L2回路电流的上升速率和下降速率。建议限流器设计中采用较小电感比,以降低FCCS 开断要求。但具体电感比取值需兼顾FCCS及耦合电抗器成本。
3) 综合理论推导和仿真分析结果发现:减小耦合系数一定程度上降低限流器线圈2 回路电流的上升速率,下降速率基本不变,可缓解FCCS 上的开断压力。但考虑到系统稳定性和快速动态响应的需求,建议限流器设计过程中采用高耦合系数。
4) 与固态式限流器相比,所提限流器的IGBT数量减少了68.6%,限流器具有较突出的经济性。
