适用于连续档装配式架线施工的线长精确计算方法

陈国庆，唐波，2，李晓斌，李恒博，张龙斌

（1. 三峡大学电气与新能源学院，湖北 宜昌 443002；2. 三峡大学湖北省输电线路工程技术研究中心，湖北 宜昌 443002；3. 广东电网有限责任公司江门供电局，广东 江门 529000）

0 引言

连续档装配式架线施工通过对线长的计算和测量代替传统的弧垂观测，解决了特殊地形、复杂天气下无法完成弧垂观测等一系列问题，在输电线路架线施工中得到了一定应用［1-2］。但由于连续档装配式架线挂线时各档应力不同，且当地形起伏时更为突出［1，3-4］，以至于采用单一导线应力进行连续档装配式架线施工的误差极大。因此，为进一步拓展连续档装配式架线施工，亟需一种线长精确求解算法。

现有研究表明［5-8］，架空线长度的微小变化对弧垂大小影响极大，这种悬链线特性使得连续档装配式架线施工工艺对线长计算的准确性要求极高。为此，文献［9］试图考虑导线塑蠕伸长对线长的影响，以提高线长计算精度。但由于线长不仅受塑蠕伸长的影响，还受耐张串长度及其自重［10-11］、杆塔挠 度［12］等其他因素影响，因此后续装配式架线线长计算研究，陆续引入了耐张串对线长的增大系数［11］、杆塔挠度折中系数［13］，最终形成当前连续档装配式架线线长的求解方法［13-14］。

但文献［12］指出，现有线长求解方法未能解决耐张段各档线路参数对档内导线应力的影响问题，以致线长计算仍不准确，由此提出了采用连续档架线的平均应力计算线长的思想。同样，文献［2］也对现有线长求解算法进行了改进，提出了代表档距法计算线长值。这两种计算方法要求线长计算必须采用单一导线应力，仅适用于平原丘陵地区连续档装配式架线。但在大高差、大档距的连续档架线中，滑轮上各档导线应力相差悬殊［15-16］，此时若仍采用单一导线应力进行线长计算，将造成较大的线长计算误差。

实际上，连续档装配式架线中，两端耐张塔架线后各档导线应力受各自档距、高差等因素影响，在线长精确计算时不能忽略各档应力的差异［8］。为此，本文考虑各档档内应力差异的影响，改变采用单一导线应力计算耐张段架线线长的传统思路，提出了一种基于连续档应力求解的装配式架线线长精确计算方法，并成功在广东江门某220 kV 输变电改造工程中实现了应用。

1 连续档装配式架线施工及其线长计算

1.1 连续档装配式架线施工

输电线路连续档装配式架线施工是指在多档连续的耐张段内架线时采用线长指标架设导线的施工工艺［5，7，12］。施工时，首先按照设计弧垂值计算出各档悬挂点之间悬线的长度；然后考虑耐张绝缘子串以及铁塔挠度的影响，计算耐张段实际导线线长并进行精确测量和划线；最后依此悬挂导线即可达到预定的竣工弧垂。连续档装配式架线施工的示意图如图1所示。

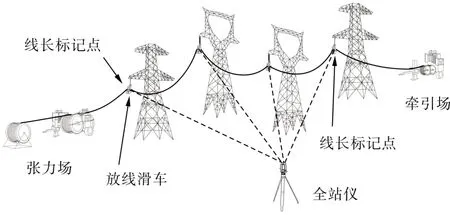
图1 连续档装配式架线施工示意图Fig. 1 Schematic diagram of continuous span prefabricated stringing construction

相较于传统架线施工方式，连续档装配式架线虽然省去了繁琐的弧垂观测与划线，但需要对展放的导线线长进行精确计算。若线长的计算值偏大，则弧垂随之增大，导致导线对跨越物或对地间隙不够，容易产生闪络；若线长的计算值偏小，则弧垂随之减小，导致导线张拉过紧，对导线防振不利，甚至影响铁塔基础和铁塔结构安全。

因此，准确计算连续档架线的导线线长是保障装配式架线施工质量的关键。

1.2 现有的连续档装配式架线施工线长计算方法

为准确计算连续档架线施工的线长，现有工程通常采用基于代表档距应力的连续档装配式架线线长求解方法。该方法在计算线长时首先需要分别求解档内有无耐张绝缘子串时无张力条件下的导线线长值［7］。

对于基于代表档距应力的连续档档内无张力下的线长计算来说，现有算法均基于导线的悬链曲线方程或斜抛物线方程［2，5，7］。根据文献［2］，在档内无耐张绝缘子串时，档内无张力条件下的导线线长为：

式中：LZi为无耐张绝缘子串各档内导线线长（i∈［2，n－1］）；n为连续档档距数量；li为第i档档距；σi为第i档导线应力；γi为第i档导线比载；αi为第i档导线悬挂点的高差角。

在有耐张绝缘子串时，档内无张力条件下的导线线长为：

式中：LNi为有耐张绝缘子串各档内导线线长（i=1或n）；λi为第i档耐张绝缘子串长度；ki为第i档的线长增大系数；yi为两端耐张塔挂线后两端导线悬挂点的挠度位移。

计算完LZi和LNi后，将两部分线长相加即可得到整个连续档装配式架线线长L为：

式中：L为连续档装配式架线施工的导线长度；LNn为第n档有耐张绝缘子串档内导线线长。

式（1）—（2）中，导线比载γi、档距li、高差hi、高差角αi、耐张绝缘子串长度λi、线长增大系数ki和挠度位移yi均可由线路前期设计确定［5］，而唯独σi难以实际测量，只能通过理论计算求解。因此，σi是保证线长精确计算的关键参数。

现有的连续档装配式架线线长计算均假定σi为定值，即各档应力相等，均为代表档距对应的应力［1，8］。然而，在实际施工中，两端耐张塔挂线后连续档各档内的导线应力受高差、档距等因素影响，各档的导线应力并不相同。这使得将连续档各档导线应力视为等应力值的代表档距法，仅适用于地形平缓且无高差时，各档导线应力相差不大的连续档装配式架线线长计算。

当地形起伏时，滑轮上各档导线应力相差更为悬殊。此时连续档各档导线应力不相等，倘若仍采取现有忽略各档应力差异的装配式架线线长计算方法，将导致严重误差。为此，本文根据连续档内各档导线应力的实际差异，对传统代表档距应力算法进行改进，基于连续档内导线总长度的变化规律，推导带放线滑车的连续档架空线应力求解方程，精确计算连续档内各档导线应力。然后，考虑耐张绝缘子串、杆塔挠度等因素对连续档耐张段线长的影响，提出了一种适用于连续档装配式架线施工的线长精确计算方法。

2 采用线长精确计算方法的连续档装配式架线线长求解

2.1 整体求解思路

采用线长精确计算方法的连续档装配式架线线长求解的关键在于，如何准确构建连续档各档导线水平应力之间的力学方程，同时对该方程进行求解获取各档导线应力精确值。

如图2 所示的连续档，由于连续档内由滑轮悬挂的导线可在各档间自由窜动，因此可以将整个连续档视为一个档。这样，单个档内任意两点间应力关系的结论在整个连续档内同样适用，即整个连续档内的导线具有任意两点间应力差等于该两点间高差与比载乘积的特性。但对于具体的第I基铁塔滑轮两侧出口处，i档侧和i+1 档侧导线轴向应力而水平应力σi≠σi+1，造成该基铁塔悬垂绝缘子串偏移ηI，使第i档线路的档距变为li+ Δli，高差变为hi+ Δhi。需要说明的是，Δhi和Δli可为正负，图2第i档中均为负。

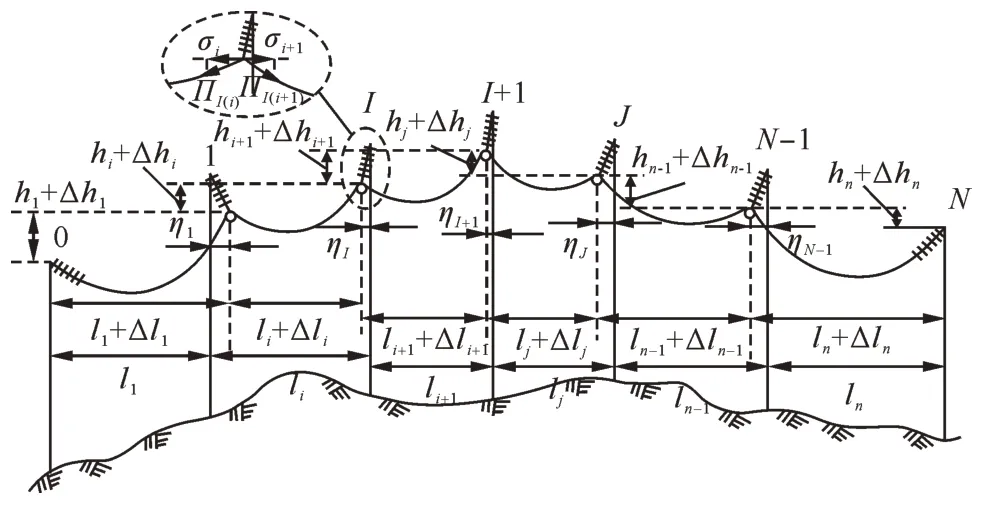
图2 滑轮悬挂导线的连续档示意图Fig. 2 Schematic diagram of continuous span wire suspended by pulleys

基于此，首先根据任意两点间的应力关系可构建连续档内第I基与第J基任意两基铁塔上悬挂点处导线轴向应力和之间的力学关系等式，然后根据档内悬挂点应力公式［5］将关系等式中的导线轴向应力用水平应力表示，即可得到连续档内第i档与第j档任意两档导线水平应力σi和σj之间的力学方程。此时，只需将任意两档中的一档应力取为已知条件，即可推求任意一档导线水平应力σi。

另外根据任意两点间的应力关系可知，连续档内最高悬挂点处导线的应力最大，为保证该最大值不超过允许应力，可将该最大值作为允许应力。

结合上述两点考虑，此时将连续档内最大导线应力作为一档已知条件，建立导线最大应力与连续档内其他各档导线水平应力σi之间的力学方程，以此求解各档导线水平应力σi。

在上述推导中，引入了未知量Δhi和Δli，这是由于悬垂绝缘子串存在偏移量ηI，因此若想继续求解σi，还需建立导线悬挂点的力矩平衡方程以获得连续档内悬挂点偏移量ηI与导线水平应力σi的关系；同时根据图2 中ηI与Δhi和Δli的几何关系，可建立这3 个参量的关系式。因此，对于一条含有n个档距、n+1 基铁塔的连续档，存在σi、ηI、Δhi和Δli共4n+1 个未知参量，且连续档首末两基耐张塔使得η0= 0 和ηN= 0，η0、ηN分别为第0 基和第N基铁塔绝缘子串偏移量，则求解剩下4n－1 个未知量需要建立4n－1个关于未知量的方程。

最终，装配式架线时连续档的线长求解流程如图3所示。

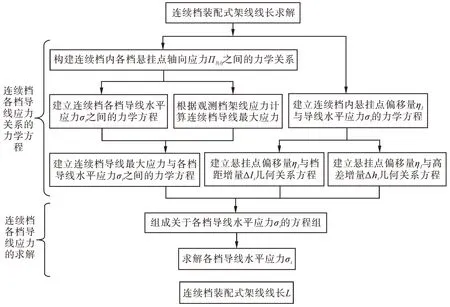
图3 基于滑轮架线时连续档的线长求解流程图Fig.3 Calculation flow chart of the wire length of the continuous span wire suspended by pulleys

2.2 连续档各档导线应力关系的力学方程

2.2.1 各档导线水平应力之间的力学方程

如图4 所示，当滑轮两侧出口处的导线轴向应力和不相等时，滑轮将向轴向应力大的一侧转动，直至滑轮两侧出口处导线轴向应力和相等，此时导线受力平衡。

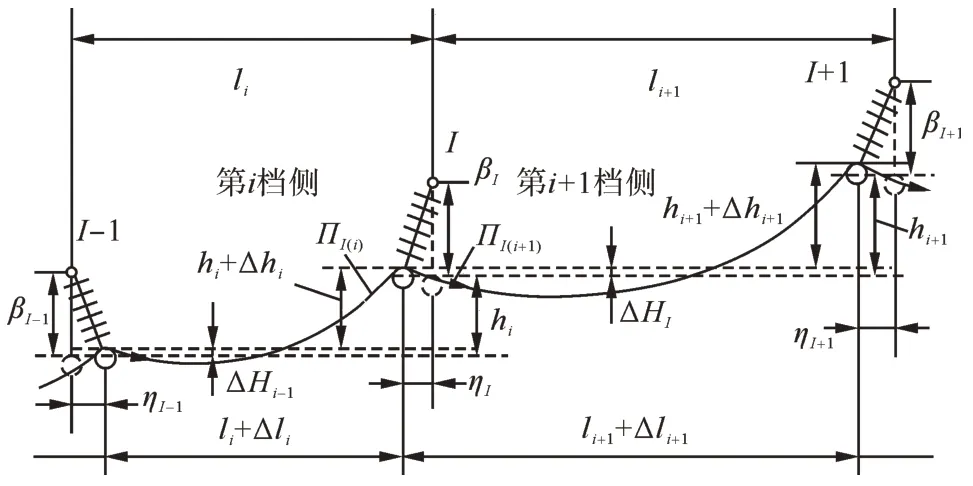
图4 连续档内相邻两档滑轮悬挂导线示意图Fig. 4 Schematic diagram of wire suspended by two adjacent pulleys in continuous span

导线受力平衡后，悬挂点相比于原铅垂位置产生了顺线路方向的水平偏移ηI，使得原档距li、高差hi分别增加了Δli、Δhi。根据导线悬挂点应力计算公式［1-3］可定义第I基铁塔悬挂点两侧导线轴向应力和与档内水平应力σi和σi+1的关系式为：

其中：

式中：为第I基铁塔导线悬挂点i档侧的导线轴向应力；σi为第i档导线水平应力；Δli为第i档档距改变值；Δhi为第i档高差改变值。

导线受力平衡后，第I基铁塔导线悬挂点处有=，根据式（4）可推得连续档内相邻两档导线水平应力σi和σi+1之间的力学方程为：

在得到相邻两档σi和σi+1之间的关系后，任意两档σi和σj之间的关系需要考虑该两档间线档高差的累加。由于第I基与第J基两基铁塔悬挂点之间的高差为应力相差因此连续档内第i档和第j档任意两档导线水平应力σi和σj之间的力学方程为：

式中hx为两档之间第x档的高差，且有正负，其符号与垂直档距中高差符号判别一致。

2.2.2 导线最大应力与各档水平应力间的力学方程

为求解连续档导线的最大应力，首先应根据计及塑蠕伸长影响的导线状态方程，计算观测档的架线应力；然后以此应力值为已知量求解连续档导线最大应力。

文献［2］采用导线状态方程公式计算观测档架线应力σ0，式中除降温值Δt以外，其余参量均可由线路前期设计确定［5］。而Δt在装配式架线施工中和传统架线施工存在差异，其取值应根据实际施工需补偿的塑蠕伸长确定［17-19］。确定塑蠕伸长时，由于装配式架线施工省去了传统架线施工中繁琐的紧线过程，这使得导线在原本紧线过程中因反复受力而自然产生的一部分塑蠕伸长并没有得到释放，因此这一部分塑蠕伸长需在Δt中进行额外补偿。即确定装配式架线施工时的Δt时，除需补偿架线后残留在线档内的塑蠕伸长外，还应考虑架线过程中释放的一部分塑蠕伸长。但这两部分塑蠕伸长产生机理复杂，工程中难以准确计算，实际应用时只能采用导线的蠕变实验确定。

由蠕变实验确定Δt后，可采用状态方程式计算观测档应力σ0，并将σ0作为已知量求解连续档导线最大应力σk。但观测档和连续档最高悬挂点所在的档并不一定重合，因此首先可获得观测档高悬挂点导线应力σg。此时，将σ0作为已知量，根据导线悬挂点应力计算公式可得σg为：

式中：σg为观测档高悬挂点导线应力；lg为观测档档距；γ为导线比载；hg为观测档悬挂点高差；αg为观测档悬挂点高差角。

考虑到σg与σk之间存在观测档高悬挂点与连续档最高点之间的应力差值γH，可得σk表达式为：

式中：σk为连续档导线最大应力；H为观测档高侧悬挂点与连续档最高悬挂点间的高差。

最后，将式（9）求解的σk作为已知条件代入式（7），可得连续档第i档导线水平应力σi与第k档导线最大应力σk之间的力学方程为：

2.2.3 悬垂绝缘子串偏移量与导线水平应力间的力学方程

式（10）中σi、Δhi和Δli均为未知变量，此时还需增补关于未知变量的方程组成方程组，求解所有未知变量。考虑到连续档内Δhi和Δli由悬垂绝缘子串偏移产生，因此可获得悬垂绝缘子串偏移量ηI，然后以ηI为中间变量，利用图4 中悬垂绝缘子串偏移前后的几何关系，分别对Δhi和Δli进行求解。

连续档内第I基铁塔的悬垂绝缘子串受力及偏移情况如图5 所示。图5 中，FI（i）为第I基铁塔放线滑车中滑轮两侧出口处i档侧导线张力，fI（i）为FI（i）的水平分量，ηI为第I基铁塔绝缘子串偏移量，βI为第I基铁塔上绝缘子串长度，A为导线截面积，G为放线滑车的重力，G0为悬垂绝缘子串除放线滑车外的重力，BI为第I基铁塔放线滑车内的导线等效在滑轮轴上的垂直荷载，R为滑轮的半径，θI(i)为第I基铁塔i档侧导线与水平线的夹角。

图5 连续档内直线塔的悬垂绝缘子串受力图Fig. 5 Force diagram of dangling insulator string of straight tower in continuous spans

根据图5，可将悬垂绝缘子串视为刚性直棒，取悬挂点O为矩心，顺时针力矩为正，列写关于ηI与σi的力矩平衡方程为：

式中BI由垂直档距概念推导。

根据式（12）整理解得ηI：

根据图4Δhi可通过第i档内两端导线悬挂点的高差变量ΔHI与ΔHI-1相减得到，且根据图4 中几何关系，可得Δhi为：

式中ΔHI为第I基铁塔绝缘子串偏移后导线悬挂点的高差变化量。

求解Δhi后，还需对Δli进行求解。由图4中Δli与ηI的几何关系可知，第i档内两端悬垂绝缘子串偏移量ηI与ηI-1之差即为Δli，可得Δli。

最后，考虑到连续档内耐张绝缘子串固定在横担位置，这使得首末两端绝缘子串偏移量η0= 0、ηN= 0，即连续档内档距变量Δli的总和为0。

联立式（10）、（13）-（16），并对该方程组进行求解，即可得到连续档各档精确导线水平应力σi。

2.3 连续档各档导线应力的求解

根据上述求解思路，连续档导线水平应力精确求解过程中的未知参量为σi、ηI、Δhi和Δli。如图2所示，n档共有4n-1 个未知数，需要列写4n-1 个方程求解。

根据式（10）可列写n个关于σi的方程；根据式（13）可列写n-1 个ηI的求解方程；根据式（14）可列写n个Δhi的求解方程；根据式（17）—（18）可列写n个Δli的求解方程。这样4n-1 个方程组成的方程组可求解σi、ηI、Δhi和Δli的4n-1个未知数。

由于上述方程和参量较多，只能采用试凑递推法变成求解，其算法步骤如下。

1） 先假定连续档第一档Δl1，代入式（15）求解得η1，根据式（14）求解得Δh1，并将Δl1和Δh1代入式（10）求解得σ1，再将σ1和η1代入式（13）求解得σ2。

2） 将Δh2取为0，根据σ2由式（10）求解得Δl2，依次利用式（15）—（14）求解η2和新的Δh2。将新的Δh2值作为初值，反复执行上述操作，使求解的Δl2、η2和Δh2再无明显变化，再根据σ2和η2由式（13）求解得σ3。

3） 此时下一轮计算将从σ3开始，重复2）中过程，直至求解出Δln，最后根据式（16）求解的ηN若为0，则上述未知参量求解正确，否则重新假定Δl1的初值。

最终，将Δhi和Δli代入式（5）得到cosαi，将σi和cosαi代入式（1）和式（2），并将计算出的LZi和LNi代入式（3），即可求得连续档装配式架线线长L。

3 广东江门某220 kV 输变电改造工程的应用

3.1 工程概况

广东江门某220 kV 输变电改造工程，改造线路从原29 号铁塔起至原36 号铁塔止，线路总长约2.89 km。具体包括拆除原36 号铁塔并新建一基终端耐张塔（36 号铁塔）、重新展放29 号铁塔至36 号铁塔段导、地线（重新放导、地线约6.382 km）。新建导线型号为2×LGJ-400/35 钢芯铝绞线［20］，送检导线样品蠕变试验的塑蠕伸长率ε为559 mm/km（25%RTS），导线具体参数见表1。

表1 导线参数Tab.1 Wire parameters

2021 年6 月14 日，选择该区段内的耐张段（29号－30 号－31 号铁塔），对耐张段内线路右相分裂导线中左子导线进行了基于线长精确计算的连续档架线施工实践。白天温度为30 ℃，无冰［21-23］。该耐张段铁塔现场复测数据如表2和表3所示。

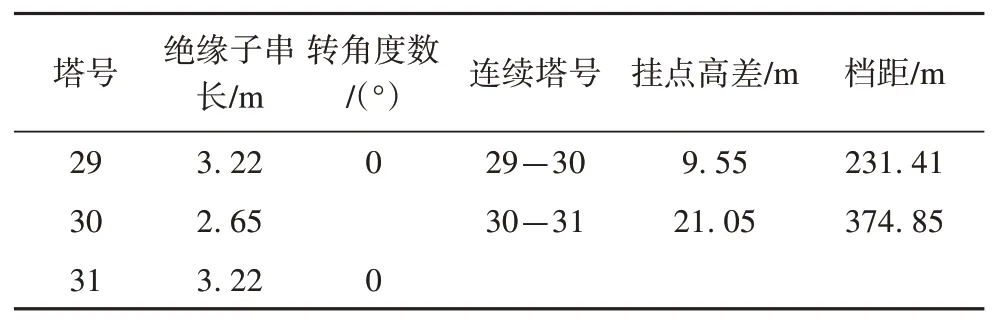
表3 线路参数Tab.3 Transmission line parameters

3.2 线长精确算法的应用过程

针对该区段右相分裂导线中左子导线的架线施工，本文取右相导线线路参数，导线具体参数见表1。 根据表1， 该型号导线自重比载为31.11×10-3MPa/m，根据2.2 节中连续档应力求解方法精确求解各档导线水平应力。首先，根据表2和3 的数据，由式（7）建立连续档各档导线水平应力之间的力学方程。然后，在计算连续档导线最大应力时，线膨胀系数μ取20.5×10-6/℃，结合2.2.2节对Δt的分析， 根据文献［1］计算降温值Δt=ε/μ=27.27 ℃，架线应力为41.32 MPa。进一步计算观测档设计弧垂时，根据观测档选取原则，选取30－31 号档作为观测档，并取lg=374.85 m，计入高差计算观测档设计弧垂为13.28 m。此时根据表3 中的数据可知，观测档和连续档最高悬挂点所在的档重合，根据式（8）求解导线最大应力σk=42.14 MPa，再根据式（10）建立导线最大应力σk与连续档各档导线水平应力σi之间的力学方程。最后，根据双联双悬挂悬垂绝缘子串设计参数，取βI=2.65 m，G0=431.71 N。根据放线滑车参数，取R=0.2 m，G=107.8 N。根据2.4 节带放线滑车架空线应力精确求解方法求解各档σi。

最终，将σi代入式（1）和（2）可得LZi和LNi，并根据式（3）求解连续档装配式架线线长L。需要说明的是根据式（2）计算档内含耐张塔的导线线长时，应考虑线长增大系数ki和横担挠度位移yi。29号铁塔和31号铁塔耐张塔的耐张绝缘子串重451.78 N，按表3中的数据计算k1=1.067、k2=1.053 和y1=0、y2=0。ki和yi的求解过程可参考文献［10，16］，此处不再赘述。

施工细节如图6 所示，架线施工时采用接触式测长设计的接地滑车配合牵张机完成导线长度的高精度测量，一旦导线的展放长度达到预警长度，施工人员对牵引设备进行制动停机，进行精准划线操作。最终通过对放线长度进行精确控制，免去了繁琐的紧线与弧垂观测过程，挂线后即可得到设计的弧垂。

图6 基于线长精确计算的连续档装配式架线施工现场Fig. 6 Construction site of continuous spans assembly prefabricated stringing based on accurate calculation of wire length

3.3 线长计算结果分析

为验证本文连续档装配式架线施工的线长精确计算方法是否准确，分别采用传统的连续档装配式架线施工线长计算方法和本文方法，对广东省某220 kV 输变电改造工程中29－31 号连续档装配式架线施工进行线长计算分析，并将分析结果与实际工程中的架线情况进行对比。

3.3.1 传统连续档装配式架线线长计算

根据文献［2］，利用传统连续档装配式架线施工线长计算方法计算时，计算结果如表4所示。

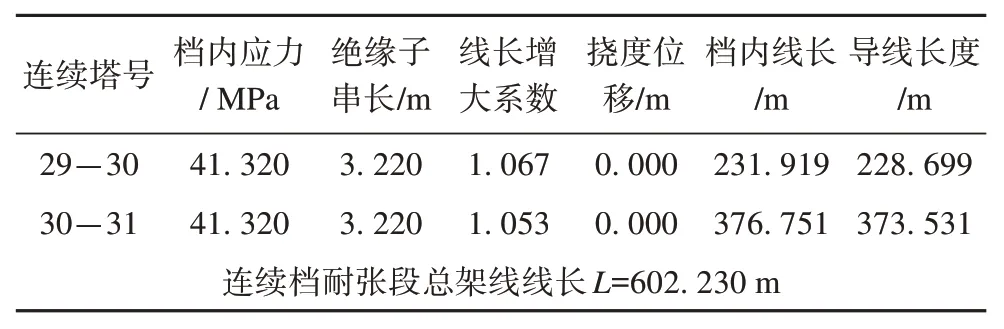
表4 传统方法计算结果Tab.4 Calculation results of traditional methods

从表4 中数据可知，在传统连续档装配式架线施工线长计算方法下，30－31号档线长对应的弧垂值为13.57 m，最终求得的线长为602.230 m。

3.3.2 连续档装配式架线施工线长精确计算

通过3.2 节的分析，此时采用带放线滑车的连续档架空线应力求解方法计算导线长度，30－31号档线长对应的弧垂值为13.45 m，最终求得L=602.209 m，计算结果如表5所示。

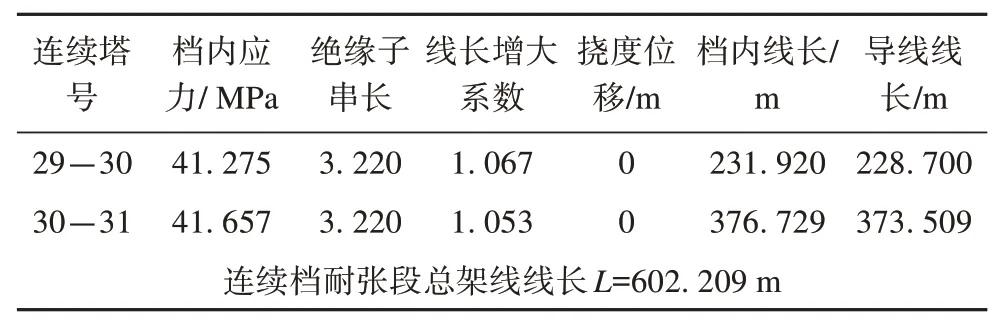
表5 本文方法计算结果Tab.5 Calculation results of the proposed method

根据《110～500kV 架空送电线路施工及验收规范》（GB50233－2005）［24］可知，导线弧垂验收值应控制在设计值的+2.5%，-2.5%，弧垂观测档的数量应根据现场条件适当增加，不得减少。按线路设计要求，30－31号档观测档理论计算线长对应的弧垂与设计数据对比如表6所示。

表6 施工结果Tab.6 Results of the construction

从表4 和5 的计算结果可知，传统方法和本文方法计算得到的30－31 号档观测档理论线长分别为373.531 m 和373.509 m，两者的相对误差百分比为0.005 9%，表6 中两种方法计算得到的弧垂分别为13.57 m 和13.45 m，两者的弧垂误差已达0.12 m，两者的弧垂误差百分比已达0.884%。这说明线长的微小变化将引起弧垂的巨大变化，线长的精确计算对装配式架线工艺而言十分重要。

从表6 数据可知，基于线长精确计算的连续档装配式架线施工结果符合验收规范，其对应的架线弧垂误差均在规范允许范围内，30－31号档观测档内基于线长精确计算的弧垂与验收弧垂偏差率仅为+1.280%。而在传统连续档装配式架线施工线长计算方法下，观测档由线长计算的弧垂值与验收弧垂偏差率为+2.184%。这说明本文考虑耐张段内各档应力差异的线长精确计算方法适用于连续耐张段装配式架线施工的线长计算。

同时，基于线长精确计算的连续档装配式架线施工验收时，实测弧垂与设计弧垂的误差为+2.108%，符合验收规范。实测弧垂与本文方法计算的理论弧垂的误差为0.818%，这是由施工误差导致的，考虑到施工误差不可避免，因此要求线长计算应更为准确。这说明本文所提线长精确计算方法适用于连续档装配式架线施工。

4 结论

本文基于连续档装配式架线施工的特点，提出了线长精确计算方法，从计算和测量的结果来看，弧垂偏差满足施工要求，并开展了如何准确评估其施工质量的工作，具体结论如下。

1）连续档装配式架线施工由于耐张段内各档档距、高差参数差距显著，导致连续档内各档应力差异显著，若忽略这种差异，将直接影响架线施工质量。因此，本文在传统的连续档装配式架线施工基础上，将原连续档代表档距应力用各档精确计算的应力替代，进而提出连续档装配式架线施工的线长精确计算方法。

2）广东省某220 kV 输变电改造工程的连续档装配式架线施工实践表明，采用基于线长精确计算方法的弧垂值为13.45 m，满足该工程的验收指标。因此建议今后连续档装配式架线施工的线长计算必须考虑各档应力差异。