基于多参数规划的主配网协同优化运行方法

姜拓，方必武，陈亦平，张勇，杨林，王科，何剑军

（中国南方电网电力调度控制中心，广州 510663）

0 引言

为了解决日益凸显的能源安全、环境污染、气候变化等问题，我国目前正积极地推进电力系统低碳化、清洁化、可持续化转型，而建设高比例新能源渗透的新型电力系统是实现上述目标的有效途径［1-2］。针对新型电力系统建设，低电压等级下分布式新能源的大规模接入是典型场景之一，引起工业界和学术界广泛关注［3-5］。伴随着分布式新能源的接入，传统配电网在运行特性上发生了深刻变化，带来了诸多新的机遇和挑战。一方面，分布式发电资源的丰富使得供电灵活性与经济性得以有效提升，降低了对主网集中式电源的供电依赖性，配网运行模式逐步从被动参与向主动支撑进行转换［6-7］。然而另一方面，随着分布式新能源发电容量占比提升，新能源天然的随机特性导致了配网净负荷波动性增强，这给主配网之间边界功率的匹配带来了额外负担，此时若无法有效地协调主配网内的资源，将导致局部电网出现功率不平衡、电压越限等系统安全风险［6］。

为了应对上述挑战，主配网之间从传统的互为边界的割裂运行方式向协同运行方式进行转换是一种合理的选择，已经成为近年来研究的热点［8-10］。文献［8］提出了一种主配网分层分布式多源协调优化调度体系，结果表明调度计划制定能兼顾主配网发电资源，有助于提高电网运行经济性。文献［9］考虑分布式风电、光伏出力分布的时间-空间不确定性，建立了面向主配网的鲁棒最优潮流模型。文献［10］建立了一种同时考虑主配网发电机组的安全约束机组组合模型，并采用分层优化算法进行了求解。除了关注于主配网之间的有功功率协同之外，一些研究也关注于主配网之间的无功电压优化问题或交流潮流计算问题［11-13］。文献［11］研究了一种考虑调度需求的主动配电网分散协调无功电压控制模型，实现了变电站控制和分布式电源控制之间的协调。文献［12］针对主配网一体化潮流计算问题，提出了一种改进的牛顿法来提高计算的收敛性能。文献［13］面向含电磁环网的主配网，采用了主从分裂算法来解决全局动态潮流的分布式计算问题。

考虑到我国现行的分级调度体制下主配网通常由不同的调度机构负责调控，这意味着系统层面的协同优化目标与相对独立的运行体制之间存在着天然的矛盾。为了调和上述矛盾，一些学者针对主配网协同优化模型的分布式求解方法展开了研究［14-19］。其中，常见的分布式求解方法包括Heterogeneous 分解方法［14-16］、广义Benders 分解方法［17-18］、交替方向乘子法［19］等。由于上述分布式求解方法通常仅能进行局部信息的交互，因而面临着收敛速度慢、数值稳定性差的问题［20］。为此，一些研究注重提升上述分布式求解方法的计算性能［20］。文献［20］基于投影理论，计算出子问题投影函数在给定边界变量处的二阶展开式，相比于Benders 分解方法中采用的一阶展开式，该方法显著提升了迭代的收敛速度。

尽管如此，现有的分布式求解方法依然采用基于迭代的计算框架，这意味着在市场出清或者计划编制时，主配网的不同调度机构均需进行多轮计算来为彼此提供计算边界，并且二者之间需要频繁交互信息才能够进行完整求解，这无疑为信息通信以及计算可靠性带来了巨大挑战，同时也面临着计算收敛性方面的风险，且在当前的调度体系下是不易实现的。为此，本文提出了一种基于多参数规划的主配网协同优化运行方法。该方法能够完整地刻画配网的相关运行信息，使得协同优化过程中不同调度机构之间仅进行单次的信息交互，能够有效地避免不同调度机构之间的迭代求解过程，简化信息通信并保障计算收敛性，有利于实际工程应用。

1 主配网协同优化运行模型

本节将构建主配网协同优化运行模型，该模型基于如下基本假设：1）考虑的机组类型包括火电机组、水电机组以及风电机组，其他类型的机组（例如，燃气机组、光伏发电组件等）亦可以采用类似的方法进行处理；2）本文关注主配网之间的有功功率平衡，采用直流潮流构建电力系统潮流方程［14］；3）该模型考虑两种配网类型，分别是包含分布式电源的主动配电网以及传统配电网，且传统配电网的有功负荷作为已知参数并可通过预测手段获得。

1.1 目标函数

主配网协同优化运行模型的目标函数是最小化所有调度时段内的总运行成本，其表达式为：

式中：ΩT为调度时段的集合；ΩADG为主动配电网的集合；ΩG和分别为主网和配网k中发电机组的集合；为发电机组i在时段t内的有功出力；Ci(·)为发电机组i的发电成本函数，其中火电机组的发电成本与发电出力之间满足二次函数关系，水电机组的发电成本与发电出力之间满足线性关系，风电机组的发电成本为0。

1.2 主网系统运行约束

主配网协同优化运行模型考虑的主网系统运行约束包括以下几个方面。

1.2.1 功率平衡方程

式中：ΩTDG为传统配电网的集合；和分别为传统配电网k和主动配电网k在时段t内与主网间传输的有功功率。

1.2.2 线路传输容量约束

式中：ΩB和ΩL分别为主网内母线和线路的集合；、和分别为连接至母线b的发电机组、传统配电网和主动配电网的集合；Sbl为传输线路l的有功潮流与母线b的注入有功功率之间的转移分布因子；为线路l的传输容量。

1.2.3 机组出力上、下限约束

式中和分别为发电机组i的最大和最小有功功率出力限值。

1.2.4 机组爬坡速率约束

式中：和分别为火电机组i的最大上、下爬坡速率；Δt为调度时段的长度。

1.3 配网系统运行约束

主配网协同优化运行模型考虑的配电系统运行约束包括以下几个方面。

1.3.1 功率平衡方程

式中：和分别为主动配电网k内发电机组和供电负荷的集合；为供电负荷d在时段t内的负荷值。这里本文采用如文献［14］所给出的无损潮流方程对配网进行建模，此时若进一步考虑配网线路损耗的影响，亦有较为成熟的方法［19，21］可以进行处理，且不改变线性特性。

1.3.2 线路传输容量约束

式中：和分别为主动配电网k内的节点和线路集合；为连接至节点b的供电负荷集合。

1.3.3 机组出力的上、下限约束

1.3.4 主配网功率交互的上、下限约束

式中和分别为主动配电网k允许与主网间传输的最大和最小功率限值，可以通过变压器的传输容量进行确定。

1.4 主配网协同优化运行模型的抽象数学表示

式（1）—（9）共同组成了主配网协同优化运行模型的数学表达，其所有约束条件均为线性约束，同时考虑到配网中多有功接入分布式水电，其运行成本项具有线性结构。式（10）—（12）分别给出了主配网协同优化运行模型的目标函数、主网系统运行约束、配网系统运行约束的抽象数学表达形式。

式中：PG和分别为主网与配网k内机组出力构成的向量；为主动配电网k与主网间传输功率构成的向量；A、Bk和b为输电系统线性运行约束的系数矩阵（向量）；Ck、Dk和dk为配网k线性运行约束的系数矩阵（向量）；ck为配网运行成本表达式的系数向量。可以看到，配网与主网间传输的有功功率同时出现在二者的运行约束式（11）—（12）中，这表明传输功率同时对主、配网的有功平衡和运行边界产生了影响，也体现出主、配网之间边界功率匹配的必要性。

2 基于多参数规划的主配网协同优化运行模型求解

2.1 主配网协同优化运行模型的重构

由式（10）—（12）可知，配网与主网之间传输的有功功率是二者运行约束耦合的关键所在，因此可以基于这部分耦合变量直观地将该模型等价地表述成如下的两步优化形式：

式中目标函数中与配电网k相关的成本函数Ck(·)可由式（14）定义。

式中P为主网与配电网k之间传输功率（所有时段）空间内的自变量。式（13）—（14）所示的等价变换提供了主配网协同优化运行模型分布式求解的基础。其中，式（14）表示在给定主配网间传输功率的基础上优化配网运行方式所能够得到的最小配网运行成本，二者间的映射关系记为Ck(P)，且这一映射关系及其定义域的求解即为配网子问题。在此基础上，式（13）进一步基于上述映射关系构建主网优化运行问题，即为主网主问题。通过依次求解配网子问题和主网主问题，可以实现原问题的等效求解。事实上，配网子问题的求解是上述分布式方法应用实现的难点，传统原始问题分解算法往往通过迭代计算结构实现。例如，Benders 分解法［22-23］通过逐步逼近的方式来实现求解。该方法通过不断求解固定耦合变量所对应的子问题，生成一系列最优割对映射关系进行下逼近，生成一系列可行割对映射关系的定义域进行外逼近。从实际工程实践角度，上述主问题和子问题迭代求解的计算结构意味着主网和配网的调控中心要反复交互计算边界，这无疑为信息通信以及计算可靠性带来了巨大挑战，同时也面临着计算收敛性方面的风险，因此如何更加可靠地求解配网子问题值得进一步探究。

2.2 基于多参数规划的配网子问题求解

上述配网子问题在数学形式上是一个多参数线性规划问题［24-26］。根据多参数规划理论，所求映射关系Ck(P)的定义域可以表示成一系列互不相交的临界域（critical region， CR）的并集，每一个临界域可以表示成一个凸多面体，且在同一个临界域内式（14）最优解处的起作用约束集和不起作用约束集是恒定的，同时映射关系是线性的。由此，当给定主配网间某一传输功率P*时，式（14）的最优解记为，相应的起作用约束集和不起作用约束集由式（15）给出。进一步，联立式（15）并消去PG，*k后，可得其所在的临界域和相应映射关系的数学表达，分别由式（16）和（17）给出。

式中：CE，k、DE，k和dE，k分别为起作用约束的系数矩阵（向量）；CI，k、DI，k和dI，k分别为不起作用约束的系数矩阵（向量）。当线性规划问题有解时，其最优解总可在可行域的某一个极点处取到，且可由dim()个起作用约束取等号下对应的线性方程组所确定（其系数向量组线性无关），此时系数矩阵CE，k可逆。

式中CR为P*所在的临界域。

事实上，由于向量P的维数通常较高（与考虑的调度时段数目相同），临界域数目通常较多。为此，本文尝试从模型的数学结构出发缩减问题规模。考虑到从分布式常规能源机组的角度考虑，一方面由于小火电机组煤耗率较高，且同目前的“双碳”目标背离，因此电网公司普遍采取“上大压小”政策逐步关停小火电机组；另一方面，分布式水电机组以其能源清洁性、出力稳定性等优点，在水能资源富集的地区得到长足地发展，因此本文考虑配网中多由分布式水电机组接入的场景。由于水电机组出力调节速率较高，因此式（6）—（9）所示的配电系统运行约束中不对机组爬坡速率进行限制。相应地，上述约束是时段解耦的。此时，式（14）所示的配网子问题可按照时段进行拆解，每一时段对应的子问题具有如式（18）所示的形式。该问题同样是一个多参数线性规划问题，可以通过上述方法求解，而此时解耦变量是一维的，模型较易求解。

式中：下标t为时段标号；自变量P为传输功率向量P在某一时段上的分量；Ckt、Dkt、ckt和dkt为系数矩阵（向量）。基于以上原理，多参数规划的配网子问题求解步骤总结如下（如图1所示）。

图1 配网子问题求解流程Fig. 1 Solving procedure of distribution network sub-problem

步骤1：初始化时段t= 1，探索步长ε＞0；

步骤2：根据配电系统运行约束式（6）—（9）确定该时段对应的系数矩阵（向量）Ckt、Dkt、ckt和dkt；

步骤3：构建并求解式（19）所示的线性规划问题，得到该时段配网在考虑运行安全的前提下允许与主网间传输的最大和最小功率、；

步骤4：初始化临界域编号n= 1，临界域下限=；

步骤5：给定P=+ε，求解式（18）所示的线性规划问题，确定最优解处的起作用约束集、不起作用约束集以及相应的系数矩阵（向量）CE，kt、DE，kt、dE，kt、CI，kt、DI，kt和dI，kt；

步骤6：根据式（20）计算线性映射关系的系数aktn和bktn，根据式（21）计算临界域上限；

步骤7：若≥成立，执行步骤8，否则令n=n+ 1并执行步骤5；

步骤8：若t=|ΩT|成立，执行步骤9，否则令t=t+ 1并执行步骤2；

步骤9：输出如下结果。

由于调度时段数目和临界域数目均是有限的，因此上述计算方法可在有限步长内收敛。

2.3 主网主问题的求解

基于配网子问题的求解结果，可以构建主网主问题如下。

然而由式（22）可知，函数Ckt()是分段线性函数，此时问题式（24）无法直接求解，为此本文将对其进行处理。考虑到多参数线性规划问题从数学上等价于凸多面体的投影问题［27］，由此可知函数Ckt()是连续凸函数，此时可以引入辅助变量并给出式（24）的epigraph等价形式，如式（25）所示。

式中Ckt为辅助变量。经过上述变换，主网主问题式（25）将建模成一个典型的二次规划问题（二次项由火电机组目标引入），这一问题目前有较为成熟的求解方法可以直接求解［28］。

2.4 主配网协同优化运行流程

基于上述推导，主配网协同优化运行流程总结如下（以省级电网优化为例，假设配网已完成集约化改造，由相应的地调监控，如图2所示）。

图2 主配网协同优化运行流程Fig. 2 Coordinative optimal operation process of transmission and distribution networks

步骤1：由中调启动主配网协同优化计算流程；

步骤2：各个地调机构准备相应配网的网络拓扑结构、设备参数等系统模型，构建配电系统运行约束并按照2.2 节的计算方法求解配网子问题，得到临界域CRk及定义在其上的映射关系Ckt(P)；

步骤3：各地调将临界域及映射关系上报中调；

步骤4：中调构建并求解主网主问题式（25）得到主网及其接入机组的最优运行方案；

步骤5：中调将主网最优运行方案中与各个配网之间传输的有功功率计划下发至各个相应的地调，上述有功功率计划表示为；

步骤6：各个地调基于与主网之间传输的有功功率计划，通过求解式（26）得到相应配网及其接入机组的最优运行方案。

可以看到，相比于传统的分布式求解方法，本文直接对配网相关运行信息进行一次性地刻画，不同调度机构之间仅进行单次的信息交互，有效地避免不同调度机构之间的迭代求解过程，简化信息通信并保障计算收敛性，有助于提升数值稳定性，更加有利于实际工程应用。

3 算例分析

3.1 算例系统描述

算例系统包含一个主网（TG）和2 个配网（ADG1、ADG2），拓扑结构如图3所示。其中，主网接入了2 个火电厂（G1、G2，装机容量分别为220 MW、100 MW）和1 个风电场（W）；配网各自接入了1 个水电厂（DG1、DG2，装机容量分别为15 MW、25 MW）和1 个风电场（DW1、DW2）。表1 提供了主网和配网的网架参数，电力负荷和风电场最大可发出力预测曲线由图4 给出。同时本文算例考虑日前时间尺度上的主配网协同优化运行问题［14］，该算例共包含24个优化时段。

表1 主网和配网的网架参数Tab. 1 Parameters of transmission and distribution networks

图4 电力负荷和风电场最大可发出力曲线Fig. 4 Electricity load and available wind power curves of wind farm

3.2 基于多参数规划的求解方法有效性检验

本节将通过对比以下3 种不同的情形来验证所提出的基于多参数规划的主配网协同优化运行方法的有效性：1）主配网分立运行（记为M_Ⅰ）；2）主配网协同优化运行且直接求解（记为M_Ⅱ）；3）主配网协同优化运行且采用基于多参数规划的求解方法进行求解（记为M_Ⅲ）。这里，M_Ⅰ用于模拟配网被动参与电网运行的情形，其中配网首先决定其运行工况，其与主网间的传输功率进一步作为边界条件用于决定主网的运行工况。M_Ⅱ考虑主配网间的协同，通过直接求解第1 节中的模型得到最优运行工况，此时的计算结果是严格最优的（但如前所述，从工程应用的角度存在较大的局限性），可用于校验其他计算结果的最优性。M_Ⅲ同样考虑主配网协同优化模型，但通过第2 节的方法进行求解。3种情形的优化结果由表2和图5给出。

表2 不同情形下的优化结果Tab. 2 Optimized dispatch results in different cases

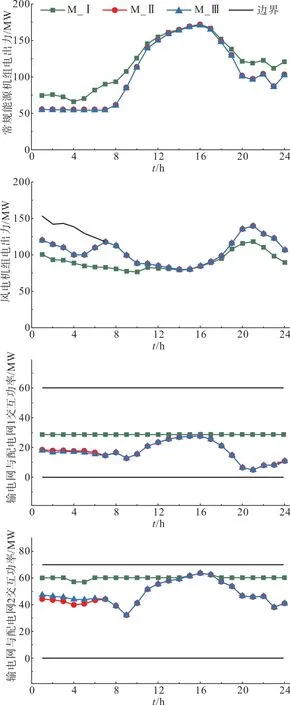
图5 不同情形下的优化结果Fig. 5 Optimized results in different cases

首先，通过对比M_I 和M_Ⅱ来说明主配网协同优化的必要性。由表2 可以看到，相较于主配网协同优化运行的情形，主配网分立运行将导致系统总运行成本增加13.95%，主网运行成本增加23.81%，系统总弃风量增加190.31%。事实上，在主配网分立运行的情形中，尽管配网1 和2 的运行成本较协同优化的情形均有所下降，局部电网获得了更优的经济特性，然而上述结果是通过牺牲主网经济特性来实现的。此时由图5 可以看到，主配网间交互功率提升，主网内火电机组需要增加出力以维持电力平衡，进而导致总运行成本和弃风电量的提升，而此时配网内的风电资源却未能得到充分地利用。换言之，此时主配网内的发电资源未能实现协同优化配置。

接下来，通过对比M_Ⅱ和M_Ⅲ来说明基于多参数规划的求解方法的有效性。在本算例中，该方法经过76.04 s 计算后得到优化结果。由表2 和图5可见，相比于M_Ⅱ中最理想的优化结果，该方法得到的优化结果在系统总成本、主配网运行成本、系统总弃风量上产生的偏差等于0，二者得到的常规能源机组和风电机组出力曲线、主配网交互功率曲线近乎重合，这反映出该方法能够实现主配网内发电资源的协同优化配置，计算结果满足最优性。另外值得说明的是，本节中M_Ⅱ与M_Ⅲ所得结果的等价性是在最优值相等的意义下得出的，而非最优解完全相同的意义下，因此M_Ⅱ与M_Ⅲ得到的最优解并不总是相同的。

事实上，相比于传统的主配网分立运行模式下主、配网之间仅交互确定的传输功率曲线，协同运行模式下二者交互的是在考虑运行安全的前提下主配网之间允许的传输功率范围，这有助于充分挖掘配网运行的灵活性，促进新能源的消纳，提高系统运行的整体经济效益。

3.3 不同因素对主配网协同优化结果的影响分析

本节将分析配网风电渗透率和配网装机水平对系统有功平衡产生的影响。为了保障结果的可比性，分析配网风电渗透率的影响时保持配网装机水平恒定，分析配网装机水平的影响时保持配网风电渗透率恒定。

3.3.1 配网风电渗透率的影响

首先讨论配网风电渗透率对系统运行产生的影响。风电渗透率在30%至70%之间变化，图6 展示了不同风电渗透率下的主配网传输功率极限，上述极限通过各个时段内的临界域上、下限表征，具体求解方法由2.2 节提供。进一步，应用基于多参数规划的求解方法得到不同风电渗透率下的系统优化运行结果，如表3所示。

图6 不同风电渗透水平下的主配网极限传输功率Fig. 6 Exchange power limit between transmission and distribution networks at different wind power penetration levels

可以看到，由于风电机组发电成本几乎为0，在配网装机容量保持不变的前提下，当风电渗透率从30%提升至70%时，系统总成本和配网成本分别下降了4.38%和23.04%。然而，由于风能资源具有较强的反调峰特性，夜间时段内风能资源较难利用，风电渗透率的提升将导致弃风量相应地增加。最后，从主配网间交互的角度，为了保障配网内有功功率的平衡，配网内风电出力的波动将引起主配网间传输功率的波动。随着风电渗透率的提升，网间传输功率的波动性增强，主网内的火电机组将增加额外的调节成本，使得主网运行成本的提升。在给定的算例中，当风电渗透率从30%提升至70%时，主网运行成本提升了5.39%。

3.3.2 配网装机水平的影响

接下来讨论配网装机水平对系统运行产生的影响。在给定的算例中，配网装机容量在100 MW 至200 MW 之间变化，图7 展示了不同配网装机水平下的主配网传输功率极限，表4 展示了相应的系统优化运行结果。

表4 不同配网装机水平下的优化结果Tab. 4 Optimized results for different installed capacity in distribution networks

可以看到，配网装机容量提升使得配网对主网内发电资源的依赖性减弱，主配网传输功率的下限下降，传输功率的可调节区域增加，配网运行灵活性提升。在给定的算例中，当配网装机容量从100 MW 增加至200 MW 时，主配网间的传输功率下降了39.17%，系统总成本和主网成本分别下降了16.72%和27.04%。

4 结论

本文提供了一种基于多参数规划的主配网协同优化运行方法。针对一个主配网协同优化问题，本文引入了多参数规划理论进行分布式求解，其中通过临界域和定义在其上的映射关系对配网的相关运行信息进行完整地刻画，从而有效避免了不同调度机构之间的迭代求解过程。通过算例仿真验证了该方法的有效性，并讨论了配网风电渗透率和装机水平对计算结果产生的影响，结果表明：1）该方法能够实现主配网内发电资源的协同优化配置，计算结果满足最优性。2）风电渗透率提升使得系统总成本和配网成本下降，但网间传输功率的波动性增强，导致主网调节成本提升。在给定的算例中，风电渗透率从30%提升至70%使得系统总成本和配网成本分别下降4.38%和23.04%，主网运行成本提升5.39%。3）配网装机容量提升可增加主配网间传输功率的可调节区域，有助于改善配网运行灵活性。在给定的算例中，当配网装机容量从100 MW 增加至200 MW 时，系统总成本和主网成本分别下降了16.72%和27.04%。

随着分布式新能源渗透率不断提升，其固有的出力不确定性、接入方式与发电上网模式的多样性将使配网运行调度面临新的挑战，如何将本文所述方法向这些场景进行拓展有待进一步探究。