基于多阶段决策的需求侧聚合响应策略

张子昊，包涛，王鹏宇，陈文皓，杨苹

（1. 南方电网数字电网研究院有限公司，广州 510663；2. 广东省绿色能源技术重点实验室（华南理工大学），广州 510640）

0 引言

为实现我国的“碳达峰”、“碳中和”战略目标，可再生能源并网的比例会越来越大，这对电网的调度工作提出了挑战［1］。一方面，可再生能源发电波动大，随机性强，仅依靠调节发电侧出力难以确保功率的实时平衡，且发电侧调节成本较高；另一方面，可再生能源发电站在风能、光能充足时段发出的电需要被实时消纳，以有效降低碳排［2］。这些都促使电力行业的学者们将目光转向调节速度快、调节成本相对低廉的需求侧可调资源上，利用需求侧可调资源参与电力系统的运行调节成为以新能源为主体的新型电力系统的核心调度关键技术［3］。

美国和欧洲对需求响应策略的研究开展较早，一直走在世界的前列，我国较晚开始探索需求响应，但随着我国电力市场的改革为需求侧响应提供了良好的发展环境［4］，国内也涌现出许多优秀的成果。文献［5］为需求侧可调资源制定了响应优先级，在进行需求响应时按照优先级调用资源；文献［6］结合区块链技术设计了一种实时需求响应的方案。以上研究将需求侧可调资源视为确定性资源，但需求侧响应一般以价格信号或激励引导用户改变用电行为，不具备强制性［7］，因此需要考虑到用户响应行为的不确定性。文献［8-9］通过挖掘用户历史用电行为对用户响应行为进行预测，优化响应策略；文献［10］利用蒙特卡罗模拟用户用电行为，以此设计合适的价格信号促进风力发电的消纳。以上文献都考虑了用户响应执行的不确定性，但并没有综合考虑需求侧可调资源具有响应速度各异的特性［11］，实时的价格信号或是响应请求无法综合利用到响应速度较慢的需求侧可调资源。将决策的时间尺度拉长可以利用更多响应速度较慢的可调资源，但同时也会面临来自响应执行、负荷预测、需求出清等多方面更多的不确定性［12］。

针对以上问题，本文拟引入多阶段决策的方法，综合利用多类型多时间尺度的可调资源，消纳来自负荷预测、响应执行、多时间尺度的需求响应市场出清三方面的不确定性，建立多阶段聚合需求响应模型，并以负荷聚合商为决策主体设计考虑响应执行偏差风险和聚合响应收益的多阶段目标函数，形成基于多阶段决策的聚合需求响应策略，为大规模聚合利用需求侧可调资源，支撑新型电力系统的调控奠定基础。

1 多阶段需求侧可调资源聚合响应模型

本节拟建立多阶段需求侧可调资源聚合响应模型，设计多阶段需求响应决策框架，并结合多类型需求侧可调资源的响应特性给出聚合需求响应模型。

1.1 多阶段需求响应框架

本文提出的多阶段聚合需求响应策略包括3 个不同时间尺度的响应阶段：日前响应、日内响应和实时响应［13］。为作简化处理，本文不考虑响应速度在一日以上的资源，且将响应速度各异的可调资源相应地分类为日前资源、日内资源和实时资源，其响应速度分别为提前一日及以上通知可响应、提前4 h 及以上通知可响应，提前5 min 及以上通知可响应［14］。

日前响应每隔24 h决策一次，以15 min作为一个调控基本时段，根据日前负荷预测信息，响应日前及中长期中标需求，决策各可调资源在下一日96个基本时段内的响应状态。由于不考虑响应速度在一日以上的可调资源，日前响应可以对全部的可调资源进行响应状态决策，有效综合利用了各时间尺度的可调资源。

日内响应每隔15 min 决策一次，同样以15 min为一个基本时段，根据日内更新的超短期负荷预测，响应截至决策时刻前出清的各时间尺度中标需求，决策可调资源在决策时刻后4 h 至本日结束内的响应状态。日内响应可决策的可调资源为决策时段内的日内资源。

实时响应每隔5 min 决策一次，以下一个5 min作为决策时段，根据实时测量的负荷功率，响应截至决策时刻前的各时间尺度的中标需求。实时响应可决策的可调资源只包括实时资源，在3 个响应阶段中可决策的资源数量最小，容量最小，但可以有效平抑负荷预测误差带来的响应误差，也能对可调资源响应执行偏差或是其他突发情况作出应对。

多阶段需求侧响应的时间尺度示意图见图1。

图1 多阶段需求侧响应决策时间尺度示意图Fig. 1 Sketch diagram illustrating the time scale of multi-stage demand response decision

3 个阶段的响应按照先日前，再日内滚动，再实时的优先级，按照时间顺序进行，后序的响应以之前响应决策的可调资源响应计划为基础进行部分资源响应状态的修正。各次响应可决策的可调资源数量及容量依次减少，但同时面临的不确定性也逐渐降低，因此综合了长时间尺度单阶段决策可调用资源数量多的优点和短时间尺度单阶段决策面临不确定性小的优点［15］。

1.2 需求侧可调资源聚合响应模型

常见的需求侧可调资源包括储能资源、可中断负荷、可转移负荷和可削减（增量）负荷等［16］，考虑各类型可调资源的调节特性，建立基本时段i内的聚合需求响应模型如下。

式中：PNR，j为在时段j内对可调资源请求的总响应容量；q为可调资源的数量；xj，i为可调资源i的在时段j的响应状态决策变量，以下简称状态变量；pN，i为可调资源i的响应容量。

1） 对于可中断负荷，pN，i等于其额定工作功率，xj，i取值为0 表示其不进行响应，取值为-1 表示其进行响应，即在该时段中断工作。

2） 对于储能资源，pN，i等于其额定充放电功率，xj，i为1 表示储能资源充电，为0 表示储能不充电也不放电，为-1表示储能资源放电。

3） 对于可转移负荷，pN，i等于其额定工作功率，xj，i为1表示可转移负荷转移至该时间段进行工作，为-1表示可转移负荷原计划在该时段的用电被转移出去，为0表示不进行响应。

4） 对于可削减（增量）负荷，pN，i等于其可削减（增量）的功率，xj，i为1表示其在该时间段增大用电功率，为-1 表示其在该时段内减小用电功率，为0表示不进行响应。

2 基于多阶段决策的需求侧可调资源聚合响应策略

基于聚合需求响应模型，可以确定一总响应容量请求下的多种响应策略，本文拟站在负荷聚合商的角度考虑，建立考虑负荷聚合商响应收益与响应偏差考核风险的目标函数，结合各类型可调资源响应约束条件，基于分支定界法设计求解策略，形成多阶段决策的需求侧可调资源聚合响应策略。

2.1 多阶段决策的聚合需求响应目标函数

2.1.1 日前响应目标函数

日前响应的规划时段较长，可以综合利用各类型各时间尺度的可调资源，应在本决策阶段追求负荷聚合商的调节收益最大［17］。

负荷聚合商与用户签订的聚合需求响应收益分成方式各异，本文假设负荷聚合商与用户间以固定比例进行分成［18］；另外，负荷聚合商一般不具备对用户持有的可调资源的强制控制力，因此最终的执行情况较决策计划的执行情况间一般具有一定量的偏差，可能导致负荷聚合商响应容量偏离允许范围，进而造成响应考核费用，因此应对响应偏差带来的考核风险给予考虑［19］。综上，本文设计的日前响应目标函数由两部分构成：聚合响应分成收益和响应偏差考核的条件风险价值，如式（2）—（3）所示。

式中：YDay-ahead为日前响应目标模型；kD为负荷聚合商与可调资源持有用户商定的聚合响应收益分成比例；m为有中标需求的基本时段数；QR，j为中标基本时段j的聚合响应容量；Dj为中标需求容量；PB，j为用户基线功率；RD，j为中标基本时段j的中标需求补偿价格；T为基本时段时长；(QR，j)为在置信度β下聚合响应容量QR，j执行偏差带来的响应考核成本的条件风险价值；PE，j为响应后聚合用户总负荷；PUN，j为不可控负荷在时段j的日前预测功率；PNR，j为全可调资源在时段j内计划响应容量。

聚合响应容量由Dj、PB，j、不可控负荷功率PNR，j、可调资源原总用电功率PN，j、可调资源总响应容量计算得到。

要获得(QR，j)，可先进行电力用户历史响应数据挖掘，得到实际聚合响应容量与计划聚合响应容量之比δ概率密度分布函数［20］，接着根据响应偏差量ε=QR，j·(δ- 1)与响应考核成本的关系得到响应考核成本yl的概率密度分布函数f(yl)。

式中：k1、k2分别为响应偏差允许下限、上限比例；r1、r2分别为响应欠量和响应过量的单位惩罚价格；T为基本时段时长；根据f(yl)可进一步得到yl的累计分布函数F(yl)，则可计算Vcβ(QR，j)的值。

式中Vβ(QR，j)为在置信度β下，聚合响应容量QR，j执行偏差的风险价值。

2.1.2 日内响应目标函数

日内响应的决策时段同样较长，本文同样将日内响应的目标设计为考虑聚合响应执行偏差风险的负荷聚合商收益最大。

式中YIntraday为日内响应目标模型。

其中各量的计算方法与日前响应目标函数中的类似，不同之处在于日前资源的决策变量不能在本阶段被修正，中标需求可能增多，不可控负荷功率的值由更精确的日内超短期预测值替代。

2.1.3 实时响应目标函数

实时响应的决策时段短，难以通过实时响应决策优化整日的响应收益，但实时响应面临的不确定性最小，本阶段决策应以减少响应偏差为目标［21］，以减少聚合响应容量超过允许范围的风险，如式（7）所示。

式中：Yreal-time为实时响应目标模型；kS为负荷聚合商决定的保险系数，意义为负荷聚合商认为计划的响应容量应为中标需求的kS倍时最能兼顾风险与收益［22］。

2.2 需求侧可调资源响应约束条件

开展需求侧聚合响应调控时，需遵循多类型多时间尺度的可调节资源调节约束。

2.2.1 调节时间尺度约束

定义决策阶段时间尺度标志变量ζ1∈[1，2，3]，分别表示当前决策为日前响应、日内响应、实时响应；定义可调资源调节时间尺度标志变量ζ2，j∈[1，2，3]，分别表示第j个可调节负荷为日前资源、日内资源、实时资源。记第z次调控 决 策 前 的 负 荷 调 控 计 划 为包含q个可调节资源的整日的调控计划，其中单个可调节资源一日的调控计划包含该可调节资源在m个时段下的调控状态，则调节时间尺度约束可表示为：

当可调资源调节时间尺度大于决策时间尺度时，ζ2，i-为一负数，该可调资源的工作计划因此不能在当前决策中被改变。

2.2.2 多类型可调资源调节特性约束

各可调资源具有不同的调节特性约束。对于储能资源：其荷电状态只能在0～100%间；对于可中断负荷和可削减（增量）负荷：只有在其原定工作时段才能进行响应调节，即其响应状态变量可以不为0，且其一日内的总响应时长一般具有上限约束；对于可转移负荷：其一日的总工作时长不应被改变，且原定工作时段不可作为增量调节时段，原定不工作时段不可作为减量调节时段［23］。综上，建立以下多类型可调资源调节特性约束。

式中：为储能资源i在任意时刻的荷电状态；为储能资源i在规划时段j结束后的荷电状态；为储能资源i的额定容量；为储能资源i在时段j的状态变量；为可中断负荷或可削减（增量）负荷i在时段j的状态变量；为可中断或可削减（增量）负荷的原工作状态变量，且为0-1 变量，为1表示原定在该时段工作；为可转移负荷i在时段j的状态变量；为可转移负荷的原工作状态变量，且为0-1 变量，为1 表示原定在该时段工作；为可中断或可削减（增量）负荷的一日内最大响应时段数上限。

2.3 可调资源优化调控策略求解方法

由上文给出的需求响应模型、目标函数、约束条件所构成的优化问题为一分段的线性优化问题，应首先对目标函数进行线性化［24］。

对于一个n段线性函数f(x) 的分点为[b1，b2，…，bn+1]，引入n+ 1个连续变量，可将x和f(x)表示为：

式中：wi为引入的第i个连续变量；bi为分段函数的第i个分点；f(bi)为函数分点bi对应的函数值。

同时引入n个0-1 变量zi，连续变量wi和zi需满足以下约束。

线性化后的聚合调控优化问题为一混合整数线性优化问题，可采用分支定界法进行寻优［25］。

3 算例分析

为验证本文所提策略的有效性和实用性，本文构建了包含15 个可调资源聚合体的需求响应场景，可调资源信息选取自山西某电力调峰负荷聚合商所聚合的电力用户，对其分别采用多阶段响应决策和单阶段响应决策，并对两种决策方法下的响应效果进行分析比对。

3.1 算例设计

3.1.1 需求设计

设置该负荷聚合商于该次聚合需求响应中的中标需求信息见表1所示。

该需求响应市场规定的响应越限考核单价等于补偿单价。

3.1.2 需求侧可调资源设计

该负荷聚合商于当日聚合的用户的不可控负荷日前预测功率、实际运行功率及可调节负荷原定使用计划见图2-3，可调资源详情见表2。为作简化起见，利用聚合用户日前不可控负荷预测及可调节负荷原总用电功率相加作为聚合用户基线负荷；利用聚合用户不可控负荷实际用电功率每15 min的平均值作为各日内负荷预测值。

表2 可调资源聚合体信息Tab. 2 Information of ajustable resource

图2 聚合用户负荷曲线Fig. 2 Load curves of aggregated users

图3 可调负荷原定工作时间Fig. 3 Adjustable load original working time

3.2 单阶段可调资源聚合需求侧响应效果分析

3.2.1 长时间尺度（日前）决策的聚合需求响应

本节采用单阶段日前决策进行聚合需求响应，使用的模型、目标函数、约束条件均与本文多阶段决策中的日前响应相同，决策后的可调资源计划使用情况和计划的负荷曲线见图4—5。

图5 日前决策详情Fig. 5 Details of day-ahead decision

但是，日前单阶段决策是基于日前及中长期需求、日前不可控负荷预测进行的，不能有效响应日内及实时的需求，不能针对负荷预测的误差做出修正，基于日前单阶段决策的策略进行响应后的实际负荷曲线如图6 所示，该日负荷商实际总收益为148 822.5元。

图6 日前决策实际响应曲线Fig. 6 Actual response curves of day-ahead decision

由图6 可以看出，日前决策响应后的负荷曲线在日前中标时段都能满足基本的响应精度要求，但对日内需求、实时需求则无法作有效响应，影响负荷聚合商收益，也影响电网的安全稳定经济运行。

3.2.2 短时间尺度（实时）决策的聚合需求侧响应

本节采用实时单阶段决策的方法对算例需求进行响应，使用的响应模型、目标函数、约束条件均与本文所提多阶段决策中的实时响应相同。整日经实时单阶段决策后的实时决策负荷曲线和实时决策详情见图7—8，该日负荷聚合商实际总收益-89 215元。

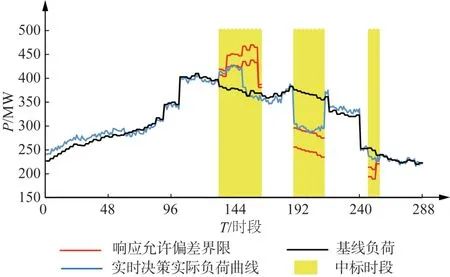
图7 实时决策负荷曲线Fig. 7 Real-time decision load curves

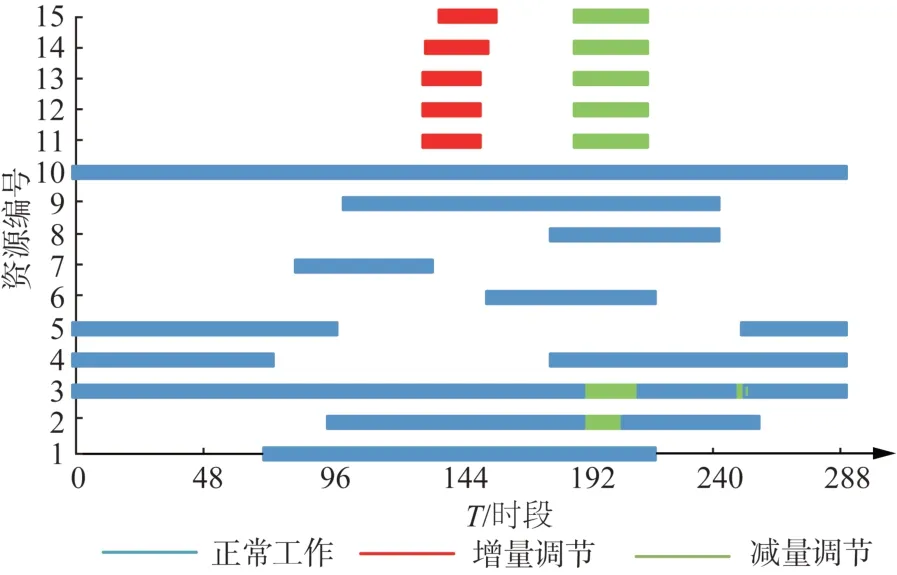
图8 实时决策详情Fig. 8 Details of real-time decision

从图7—8 可以看出实时单阶段决策并没有利用到日内资源及日前资源进行响应，只能调用实时资源进行响应，响应容量不足以满足需求。

3.3 多阶段可调资源聚合需求侧响应效果分析

3.3.1 日前响应策略

本阶段的决策情况与日前单阶段响应决策相同，可调资源状态变量的日前决策详情见图5。

3.3.2 日内响应策略

该算例在06：30 时出清了需要在11：00—11：30进行响应的需求，因此在06：45 进行的日内决策较原响应决策有较大修正。对比日前单阶段决策，为满足11：00—11：30 的填谷需求，日内资源，实时响应资源11、12、13 被调用进行充电。图9—10 为06：45 进行日内响应决策后的计划负荷曲线和可调资源响应状态决策情况。

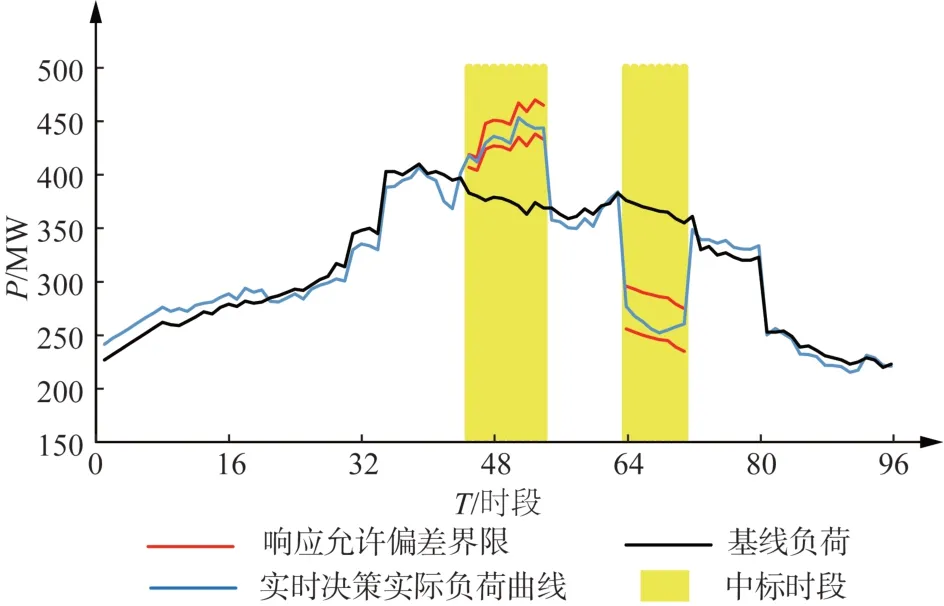
图9 多阶段决策日内（06：45）决策计划负荷曲线Fig. 9 Intraday decision planning load curves at 06:45 for multistage decision making

3.3.3 实时响应策略

各次实时决策对原响应策略做的变动较小，不便于直观比较，此处直接给出经全天多阶段决策的聚合需求响应后的实际响应负荷和可调资源状态变量，如图11—12所示。

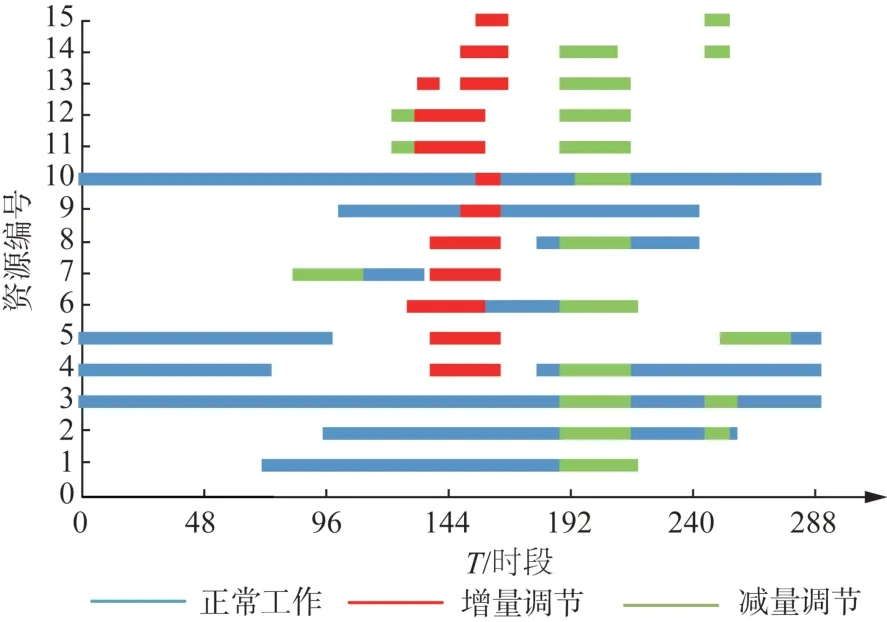
图12 多阶段决策详情Fig. 12 Details decision of multi-stage decision

从多阶段需求侧响应决策状态变量图13 可知，多阶段决策的实时决策阶段利用了实时储能资源以及实时可中断负荷资源2、3 精准响应了短时间尺度出清的实时需求。通过延长实时响应储能资源13、14、15 的充电时长满足了实时出清的填谷需求；通过调用实时可中断资源3 的中断满足实时出清的削峰需求，该日负荷聚合商实际总收益199 125元。

对比采用单阶段决策和多阶段决策的聚合需求侧响应效果（图6—7 和图11），可以清晰直观地看出多阶段需求侧的响应精度更高，能有效响应多时间尺度的需求，平抑负荷预测误差和响应执行带来的影响。

4 结语

针对需求响应交易市场、可调资源等的多时间尺度特性，本文提出了一种基于多阶段决策的需求侧可调资源聚合响应策略，具体构建了多阶段需求侧可调资源聚合响应框架，建立了考虑多类型需求侧可调资源的聚合需求响应模型，以负荷聚合商为决策主体设计了考虑聚合响应收益和响应考核风险的多阶段聚合需求响应目标函数，并给出多阶段聚合响应实施流程。最后通过算例分析对比单阶段聚合需求侧响应决策和多阶段聚合需求侧响应决策的响应效果，验证了多阶段决策可以有效响应多时间尺度出清的需求，消纳来自负荷预测误差、响应执行带来的响应偏差，提高了聚合需求侧响应的精度。

随着电力市场改革的深入，聚合需求响应将在我国电力调度工作中发挥越来越重要的作用。本文对于多类型可调资源聚合响应的建模考虑较为简单，在本文研究的基础上，更精细地优化聚合响应模型，更全面地考虑各可调资源响应特性，将有助于聚合需求响应的质量，为新型电力系统的经济安全运行提供好的服务。